某型货车车架轻量化优化设计
王海涛,肖 平,黄志凡
(安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
某型货车车架轻量化优化设计
王海涛,肖 平,黄志凡
(安徽工程大学 机械与汽车工程学院,安徽 芜湖 241000)
在货车车架设计及计算校核的基础上,以轻量化设计为目标,对车架纵梁的截面尺寸进行优化,建立优化数学模型,求出最优解,并利用有限元分析软件对优化后的车架实体模型进行了模态分析,验证其动态特性满足动力学要求,表明该轻量化优化设计的合理有效。
车架;轻量化优化设计;模态分析
0 引言
随着近年来经济的高速发展,空气污染所形成的雾霾现象也日趋严重,汽车尾气排放作为形成雾霾的重要因素之一,已经引起了人们的高度关注。如何实现汽车节能减排已成为业界人士研究的重要课题。大量实验和实践证明,汽车轻量化是降低汽车排放和减少燃油消耗率的最有效措施之一[1]。汽车重量降低1%,油耗可降低0.7%,并且汽车质量的减小可以使其加速性能得以提高,同时由于惯性变小,其制动距离也将减少[2-5]。本文以货车车架为对象,匹配选型发动机,从车架设计入手,结合传统的经验设计法、简化计算法和有限元分析法对车架进行了轻量化优化设计,给出了车架设计及轻量化优化设计的一种思路,结合优化计算与有限元软件进行综合分析,结果显示设计符合要求,达到了车架轻量化优化设计的目的。
1 车架设计参数确定及计算校核
某型货车载重量为5000kg,最大拖挂6000kg,长 6910mm,宽2470mm,轴距3950mm,最高车速90km/h(单车),匹配有东风EQ6100发动机,额定功率99kw,最大扭矩353Nm,额定转速1600rpm,怠速550rpm,发动机正常工作时经常使用转速为1200rpm左右。
1.1 车架设计参数
由于本货车载重为5t,其后轴受载较大,根据汽车专业标准及同类车型实测,结合传统设计经验,该车架宽度设为960mm;车架长度是指车架纵梁前端面到后端面之间的距离,为满足车架技术资源的统一规范要求,减少车架品种,在设计车架过程中,车架纵梁的长度一般接近汽车长度,其值约为1.4~1.7倍汽车轮距,由于某型货车其轴距为3950mm,车身总长为6910mm,基本确定车架设计长度为6700mm;纵梁截面选用槽形断面,槽形断面的纵梁具有较好的抗弯强度,结构简单,工艺性好,紧固方便,又便于安装各种汽车部件,因此被广泛运用,并且截面通常取高h与宽b的比值为2.8~3.5,由于轻、中型货车冲压纵梁的钢板厚度为5.0~7.0mm,该某型货车载重5t,属中型,故取本车架的钢板厚度t为6mm,槽宽度不大于钢板厚度的十六倍,根据经验设计槽宽b为80mm,进而设定高度h为260mm;根据安装水箱、发动机、驾驶室、货箱等部件的需要以及车架总长,共设计七根横梁;车架所受力与力矩比较大,因此,车架材料应具有足够高的屈服极限和疲劳极限,对应力集中的敏感性低,为制造方便,材料应便于冷冲压和焊接,低碳和中低碳合金钢满足该需求,故采用16Mn钢板制造车架,该材料在变形不大的工况下能保持较高性能,其屈服极限为350MPa。
1.2 计算校核
车架的相关计算校核应该结合材料力学相关知识进行车架挠度计算、支撑力和弯矩计算、纵梁截面系数计算、纵梁最大弯曲应力的计算校核等。由于篇幅有限,本文以纵梁截面系数计算、纵梁最大弯曲应力校核为例进行计算分析。
纵梁截面系数计算。由于纵梁为槽型截面,根据断面系数公式:
W=th(h+6b)/6
(1)
其中,h为槽型断面的高度,t为钢板的厚度,b为槽的宽度。由前文可知t=6mm;h=260mm;b=80mm,因此由(1)式知断面系数W为:
W=6×260×(260+80×6)/6=192400mm3纵梁最大弯曲应力校核:
δ=Mdmax/W
(2)
汽车在运动时实际受到的最大弯矩Mdmax为静态时最大弯矩Mmax与动载系数之积:
Mdmax=Mmax×Kd
(3)
Kd为动载系数,载货货车Kd=2.5,Mmax=6587Nm,则由(3)式知:
Mdmax=6587×2.5=16467.5 Nm
代入(2)式计算得,δ=85.6 MPa。为保证车架不发生损坏,纵梁最大弯曲应力不得大于纵梁材料的许用应力[δ],许用应力计算公式:
[δ]=δs/n
(4)
其中δ为材料的屈服极限,由前文知,δ=350MPa,n为安全系数,取n=1.4则由(4)式计算得[δ]=250MPa。纵梁最大弯曲应力δ≤[δ],故纵梁截面尺寸符合应力要求。
2 轻量化优化设计
以车架纵梁为例,通过数学模型计算的方法,对车架轻量化优化设计进行初步探讨,以减小车架体积,降低车架质量为目的,建立车架轻量化优化设计问题的数学模型,合理定义设计变量和约束条件,求解目标函数。
在车架长度和材料不变的情况下,轻量化设计可以通过减小车架体积实现,减小车架体积在横梁不做改变的情况下只能通过减小车架纵梁的截面面积实现。本文以对纵梁进行轻量化设计为例进行探讨,由前文中车架纵梁的最大弯曲应力校核可知,设计过程中为保证车架的安全性,截面取值偏大,富余强度较多,因此可以在优化设计过程中适当减小车架纵梁的截面参数,以达到减小车架质量的目的。
由于车架计算过程中存在模型简化,所以计算时需适当提高车架的安全系数,才能保证实际应用中车架的安全可靠性,根据该车型实际应用,取安全系数n=3.5,此时,由式(4)代入计算可知,车架材料的许用应力为:[δ]=100 MPa,又由式(2)得:
(5)
δ≤[δ],当δ取最大值[δ]时,截面系数由(5)式得最小值:
经单位换算后得:
W=164675mm3
由于在车架长度和截面系数不变的情况下,减小车架体积只有通过减小车架纵梁的截面面积实现,即求得截面面积最小,根据前文所述建立数学模型如下:S=(h+2b)t
(6)
设计变量:纵梁截面的高度h,宽度b,厚度t。
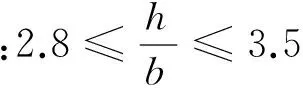
目标函数:S=(h+2b)t
根据该模型求解的参数即为优化后的设计参数。由于设计变量有3个,约束条件为不等式,在不借助计算机计算的情况下,很难得到最优设计方案,故需对模型进行简化。根据设计总结,由于钢板厚度t的值变化很小,可以将t作为定值进一步简化模型。由于类似车型的车架钢板厚度多选取6mm,在本设计中取t=6,则目标函数为:S=6(h+2b),结合式(1)可解得,当h=246.3,b=70.3时,有最优解。在保证应力要求的情况下对参数取整,取h=247mm,b=71mm,t=6mm,此时,得到比原设计更优的参数组合。此参数组合使得在满足设计要求的情况下,车架纵梁质量减小,达到了轻量化优化设计的目的。
3 车架模态分析
为防止发生共振现象,车架设计时应避开发动机怠速运转频率和发动机正常工作时的频率范围,防止车体产生共振[1]。模态分析是研究结构振动特性的数值技术,具有非常广泛的应用价值,可以帮助设计人员确定结构的固有频率和振型,因此,在车架设计时需利用模态分析对车架振型和固有频率进行研究。由模态分析理论可知,低阶振动对结构的影响最大,因此,结构的模态分析只要计算前几阶较低的固有频率和振型即可[6]。
利用有限元分析软件ANSYS进行模态分析,选用机械设计领域广泛应用的计算机辅助设计、分析和制造软件UG作为三维建模软件,根据优化设计后的参数建立车架UG三维模型,并将该模型导入ANSYS软件,进行一定简化处理后,编辑模型,划分网格并添加约束面,其有限元网格模型、约束添加图分别如图1、图2所示。

图1 有限元网格模型

图2 约束添加
将分析类型设置为模态分析Modal,双击Model进入Modal-Mechanical模块中,进行模态分析前处理,利用solution计算求解,计算时默认模态数量为6。因此,可以得到前6阶模态固有频率,见表,前6阶模态振型如图3所示。
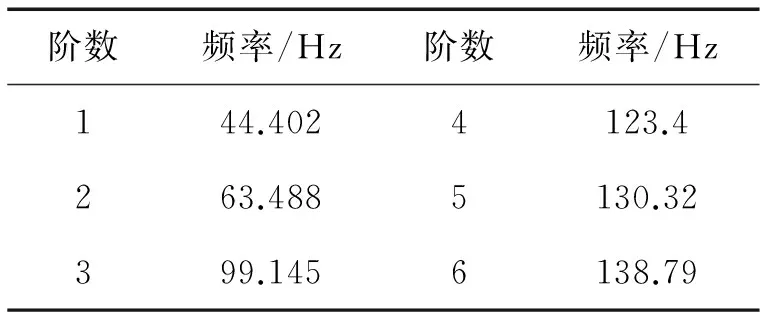
表1 车架前6阶固有频率
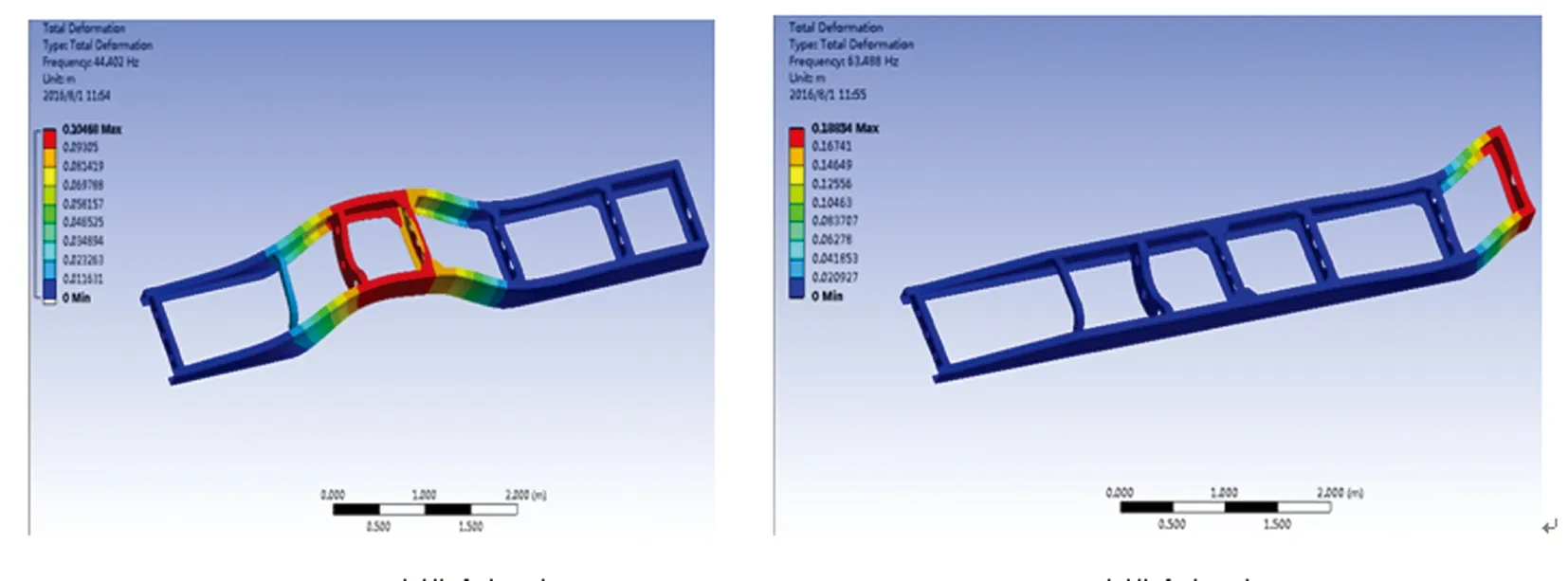
(a) 1阶模态振型 (b) 2阶模态振型
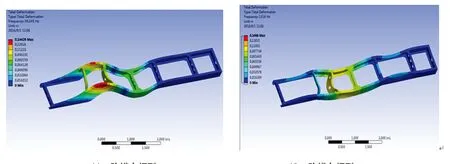
(c) 3阶模态振型 (d) 4阶模态振型
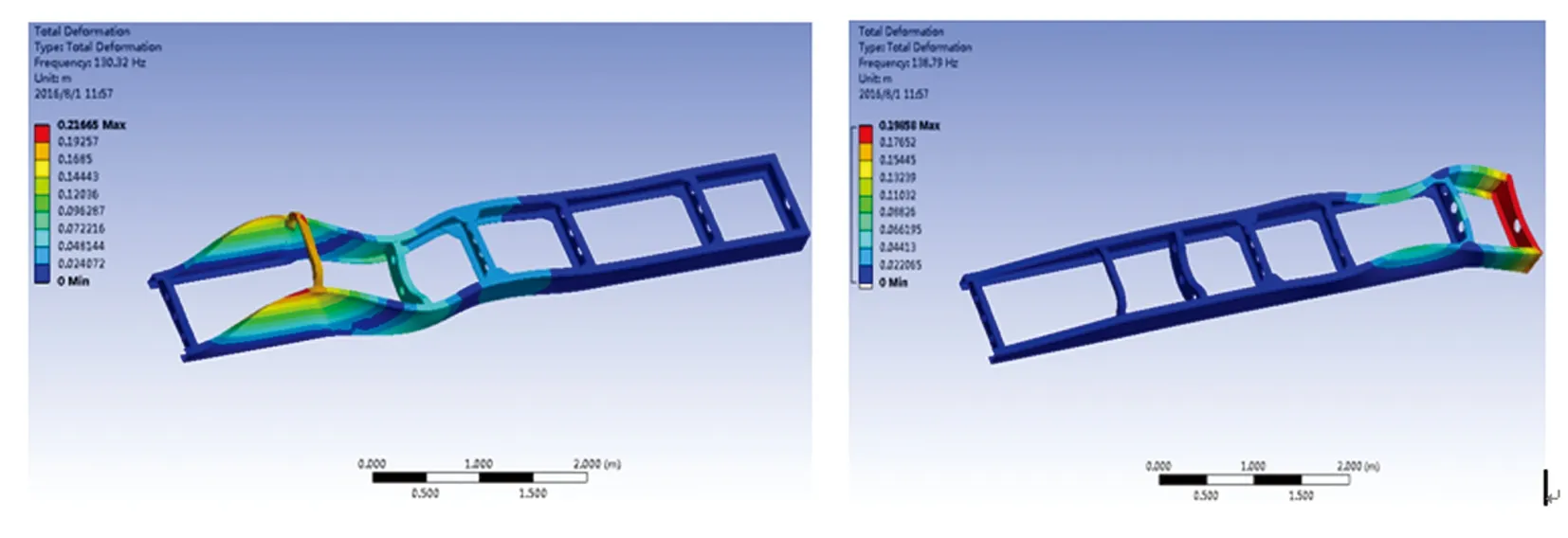
(e) 5阶模态振型 (f) 6阶模态振型
通过进行模态分析,得到了前6阶固有频率和振型图。路面激励频率一般处于较低频率,20Hz左右[7-8]。由频率表数据可知,车架的前6阶固有频率均能避开路面激励频率,从而车架能够避免发生发生低频共振的情况;该货车发动机正常工作时由其常用转速可得其振动频率约为60Hz,由于该车架的1阶模态固有频率为44.4Hz,2阶模态固有频率为63.5Hz,则该设计车架完全避开了发动机工作时的常用振动频率,能够避免因发动机工作而产生共振.因此,从模态分析验证角度来看,该车架的设计能够满足车架的动力学要求。
4 结论
以某型货车车架为研究对象,结合实际应用,依据汽车设计相关标准,按照传统的经验设计思路,从车架设计入手,完成了车架设计参数的确定及相关计算校核,并以降低车架质量为目的,确立了设计变量和约束条件,求解了目标函数,实现了车架轻量化优化设计。以优化后的设计参数建立了车架的三维模型,并将其导入ANSYS软件进行了计算求解,获得了合理的模态分析结果,初步验证了该车架的设计及优化能够满足车架的动力学要求,为车架的后期设计与研究奠定了基础。
[1] 朱晓鹏,张纪鹏,程联军,等.基于ANSYSWorkbench的某轻型货车车架轻量化设计[J].青岛大学学报,2014(3):70-76.
[2] 刘春晓.通用汽车轻量化的秘密武器[J].汽车纵横,2016(8):98-99.
[3] 王树英,郑松林,冯金芝,等. 燃料电池轿车前副车架轻量化设计[J].机械设计,2013(2):41-44.
[4] 赵韩,钱德猛.基于ANSYS的汽车结构轻量化[J].农业机械学报,2005(6):12-15.
[5] 汪伟.车架结构有限元分析与优化设计[D].南昌:南昌大学,2010.
[6] 熊永华,杜发荣,高峰,等.轻型载货汽车车架动态特性分析与研究[J].机械设计,2007(4): 60-62.
[7] 刘汉斌.基于ANSYS的轻型联合清污车车架模态分析[J].汽车零部件,2010(3):71-74.
[8] 徐杰君.叉车门架的有限元分析及动态仿真分析[D].西安:西北农林科技大学,2009.
(责任编辑:孙文彬)
Lightweight Optimization Design of a Certain Type Truck Frame
WANG Hai-tao,XIAO Ping,HUANG Zhi-fan
(Faculty of Mechanics and Automotive Engineering, Anhui Polytechnic University, Wuhu Anhui 241000, China)
Based on the design of the truck frame and checking calculation, with the goal of lightweight design, the section sizes of the longitudinal beams of the frame were optimized, the optimization mathematics model was established and the optimal solution was obtained thereby. The analysis of the optimized frame entity model was carried out by using the finite element analysis software. It is verified that the dynamic characteristics can meet the requirements of dynamics, indicating that the lightweight optimization design is reasonable and effective.
frame; lightweight optimization design; modal analysis
2016-12-27
安徽省高等教育提升计划省级自然科学研究基金项目(TSKJ2015B06);国家自然科学基金项目(51575001);
安徽省自然科学基金项目(1508085ME70);安徽高校自然科学研究项目(KJ2016A799)
王海涛(1983-),男,安徽亳州人,工程师,硕士,主要从事机械、电子技术研究。
U270.2
A
1009-7961(2017)03-0065-05

