罕遇地震作用下高铁桥梁动力弹塑性响应分析
梁升建
(淮安市交通控股有限公司,江苏 淮安 223001)
罕遇地震作用下高铁桥梁动力弹塑性响应分析
梁升建
(淮安市交通控股有限公司,江苏 淮安 223001)
为研究连续梁桥在罕遇地震作用下的弹塑性响应,基于Midas Civil建立三跨连续梁桥有限元模型。对比分析无轨、有轨两种桥梁模型的振动特性,并输入不同地震动荷载组合,对比分析罕遇地震作用下连续梁桥的动力弹塑性响应。研究表明,无轨和有轨桥梁自振特性有较大差异,有轨模型自振周期相对较大;罕遇地震作用下桥墩墩底进入弹塑性状态,产生塑性铰。
高铁桥梁;罕遇地震;振动特性;弹塑性反应
0 引言
随着经济的发展、城市化建设的不断推进,我国对便利交通的需求日益凸显,其中高速铁路在我国迅速发展,截止到2015年底,我国高速铁路运营里程达2.36万公里[1]。在高速铁路线路中,桥梁是重要的组成部分,高铁桥梁的动力响应受到了诸多专家、学者的关注。夏禾等[2]采用拟静力位移法求解了非一致地震激励下车桥系统的动力响应;王少林等[3]采用双块式无砟轨道模型,分析了地震作用下高速列车-线路-桥梁系统的动力响应;鞠彦忠等[4-5]通过低配筋大比例尺铁路桥墩模型的拟静力试验,研究了低配筋铁路桥墩的延性抗震性能。既有高速铁路桥梁动力响应分析大多集中于简支梁桥的弹性分析,没有考虑桥墩动力弹塑性反应,关于桥墩的研究也局限于用单调加载试验或拟静力试验来模拟地震作用。
抗震设计的概念提出以来,抗震分析方法历经了静力到动力、弹性到弹塑性的发展过程。许多规范对弹塑性分析也都有详细规定,《建筑抗震设计规范》[6]中提出“不规则且具有明显薄弱部位可能导致地震时严重破坏的建筑结构,应按本规范有关规定进行罕遇地震作用下的弹塑性变形分析。”对于铁路桥梁,《铁路工程抗震设计规范》[7]规定应按罕遇地震对钢筋混凝土桥墩进行延性验算或最大位移分析,同时,钢筋混凝土桥墩在罕遇地震作用下的弹塑性变形分析,宜采用非线性时程响应分析法。
桥梁在罕遇地震作用下允许进入弹塑性阶段,对桥梁进行较为详细、准确的弹塑性分析并了解其在罕遇地震作用下的动力响应有助于为抗震设计提供参考和借鉴。考虑到桥梁结构的复杂性,比如边界非线性、材料非线性、几何非线性等定义以及塑性铰的定义和分配,本文基于Midas Civil有限元软件,建立了三跨连续梁桥的全桥有限元模型,对比分析了无轨和有轨两种桥梁模型的振动特性,并对三跨连续梁桥有轨模型进行了罕遇地震作用下的动力弹塑性时程响应分析。
1 工程概况
以某城际高铁三跨连续梁桥作为研究对象,桥跨全长177.5m,计算跨度为48+80+48m,截面采用单箱单室、变高度、变截面直腹板形式。桥墩采用圆端形实体墩,墩高为16m。二期恒载为160kN/m,梁体采用C50混凝土,墩身采用C30混凝土。纵向预应力钢束采用抗拉强度标准值为1860MPa的高强低松弛钢绞线,公称直径15.2mm,墩身纵筋采用直径28mm的HRB335钢筋,箍筋采用直径12mm的HRB335钢筋。该桥设防烈度为7度,场地类别为II类场地。
2 有限元模型
采用有限元软件Midas Civil建立三跨连续梁桥全桥空间分析模型,主梁和桥墩均采用梁单元模拟。三跨连续梁桥有限元模型,如图1所示。

图1 全桥有限元模型
2.1 边界非线性
该桥桥墩与梁体之间采用抗震型盆式橡胶支座连接,其支座布置形式,如图2所示:
图2 支座布置示意图
在抗震分析中需要考虑盆式橡胶支座的边界非线性特性以反映支座的减振效应,其隔震工作原理包含三个阶段:支座水平力大于设计竖向承载力的22.5%时,效能板开始滑移,为第一道隔震作用;然后阻尼圈进入工作,为第二道减振作用;当地震冲击波超过一定极限时,刚性抗震起到第三道减振作用。
对连续梁桥进行弹塑性时程分析需要求解结构在地震波输入的每一时刻的响应,因此本文在建模过程中将盆式橡胶支座的边界非线性特性按滞回模型考虑。
2.2 桥墩纤维单元模型
纤维单元将梁单元截面离散化为若干只有轴向变形的纤维,可根据定义的纤维材料的应力-应变关系和截面应变的分布形状假定较为准确的截面弯矩-曲率关系。纤维单元假定整个截面符合平截面假定且不考虑钢筋与混凝土之间的滑移。
由于纤维单元模型能很好处理各种非线性问题,求解过程稳定,适合于强震作用下整体结构的灾变过程分析[8]。所以本文采用纤维单元模型对桥墩进行非线性动力弹塑性分析。钢纤维的本构模型选用双折线型的随动硬化曲线,如图3所示,混凝土纤维的本构模型选用Kent和Park提出的对受压混凝土的包络曲线,如图4所示。
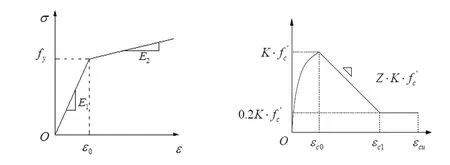
图3 钢纤维本构 图4 混凝土纤维本构
纤维本构模型中的计算参数取值,见表1和表2:

表1 钢纤维模型参数

表2 混凝土纤维模型参数
根据上述模型参数对桥墩截面按约束混凝土、非约束混凝土和纵筋划分纤维模型,如图5所示:
图5 桥墩截面纤维划分
2.3 轨道模型
为了考虑轨道对桥梁动力响应的影响,本文基于以下假定建立了轨道模型。
(1)轨道与主梁弹性连接,忽略轨道与主梁的纵向位错;
(2)假定轨道为弹性长梁。
本文选用的轨道质量集度为60 kg/m,其与主梁的横向连接刚度取为30000 kN/m,垂向连接刚度取60000 kN/m。轨道单元如图6所示。
图6 轨道模型
3 地震动的选取
地震动的特性可以通过其三要素来描述,即地震动的振幅、频谱和持时[9]。结合地震动三要素,根据桥梁本身的特性、所在场地条件选择合理的适量的地震记录。
3.1 频谱特性
由该桥位于7度区,场地类别为II类,根据《铁路工程抗震设计规范(GB 50111-2006)》表7.2.4-2可得桥梁所处场地地震动反应谱特征周期Tg=0.4s,所选地震动的特征周期要与该值接近,地震动特征周期求解公式如下:
地震动的特征周期:Tg=2π*EPV/EPA。
EPV与 EPA分别为地震动有效峰值速度和地震动有效峰值加速度,其值可通过《中国地震烈度区划图》中规定的计算方法取得。根据上述方法,本文选取了符合条件的三条典型地震动,见表3。

表3 地震动频谱特性
3.2 幅值
根据《建筑抗震设计规范(GB50011-2010)》表5.1.2-2可得罕遇地震下时程分析所用地震加速度时程的最大值220 gal,即2.2 m/s2,取之为设计加速度有效峰值(设计EPA)。由地震动EPA与设计EPA可得选用地震动加速度的幅值调整系数:
水平调整系数=设计EPA/EPA
竖向调整系数=0.65*水平调整系数
根据上述公式计算结果见表4。
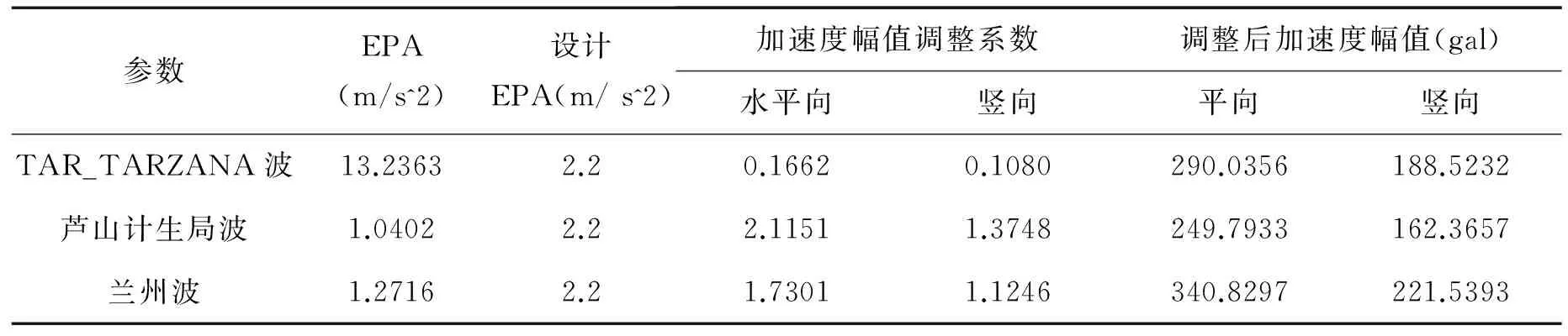
表4 地震动加速度幅值
3.3 持时
地震动的一般持续时间取结构基本周期的5~10倍,为更好地了解结构在罕遇地震作用下的反应,本文三条地震动持续时间均取为20 s,查表基本周期的17倍。
4 模态分析
模态分析是判断结构是否合理的重要依据,也可为结构动力特性的优化提供依据。通过前文建立的有限元模型分别对单桥模型和考虑轨道的全桥模型进行动力特性分析,在Mida Civil中根据特征值分析结果显示前60阶振型的参与质量,顺桥向(X向)为99.6%,横桥向(Y向)为99.46%,竖桥向(Z向)为99.17%,均满足振型参与质量达到结构总质量的90%的要求[10]。表5列出了结构前10阶自振频率及振型,从表5中可以看出,当考虑轨道模型时,结构自振周期变大,其中第1阶振型周期增量最大,从第5阶振型开始,相邻振型周期之间的差逐渐变小。分析可知:1)轨道模型对结构的自振特性影响较大,在模拟分析中不容忽视;2)结构的抗弯刚度相对较大,主要体现为低阶振型的弯曲振动。
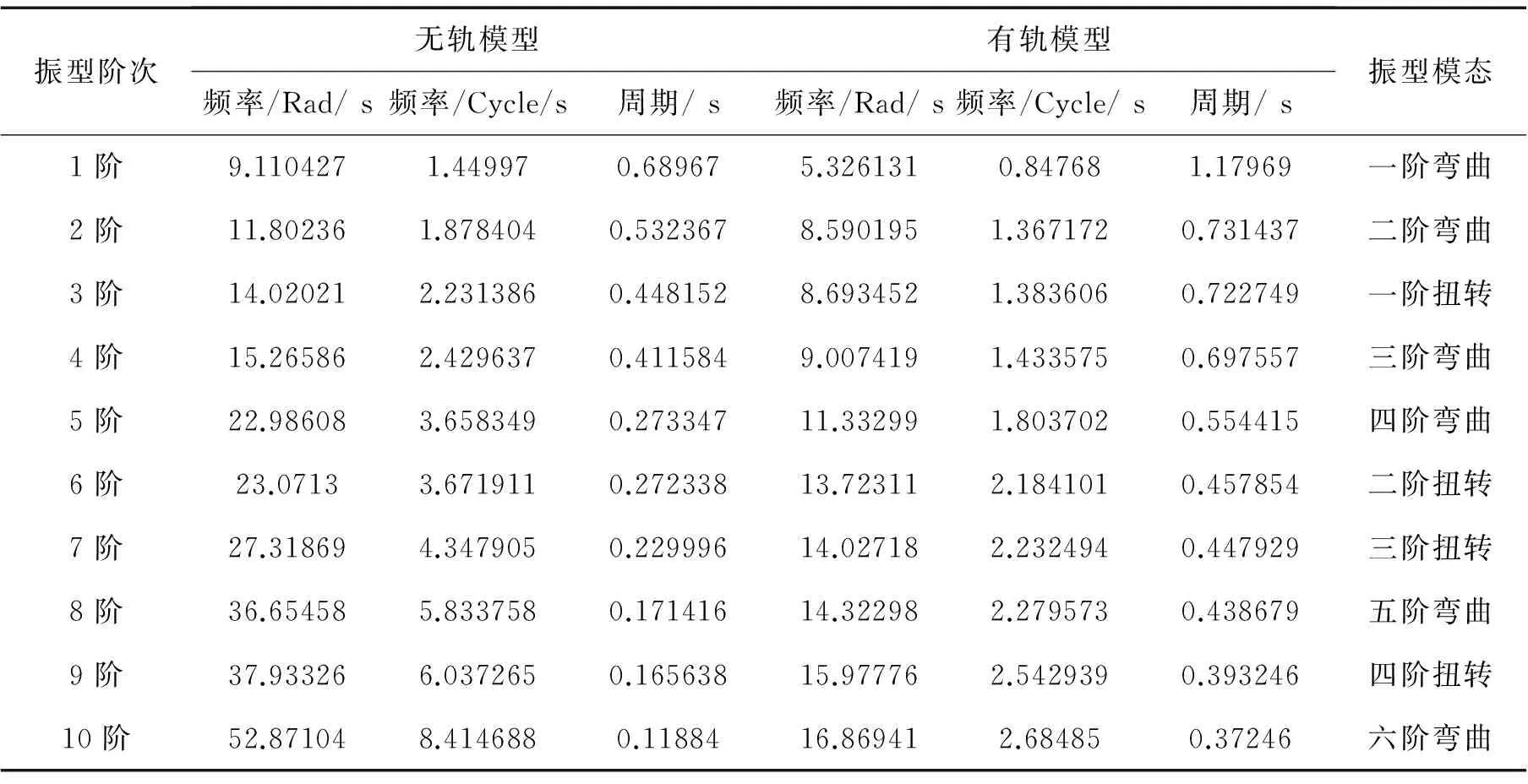
表5 结构前10阶自振频率及振型
5 动力弹塑性反应分析
沿顺桥向和横桥向输入地震动加速度时程,同时考虑竖向地震动作用,分析了有轨桥梁模型在三条地震动不同荷载组合(顺桥向+竖向地震组合Ex+0.65Ex、横桥向+竖向地震组合Ey+0.65Ey)作用下的反应。
5.1 桥墩塑性铰状态
在地震动作用下2号桥墩墩底单元首先进入弹塑性阶段,形成塑性铰,随着作用时间的持续,塑性区域从桥墩底部向桥墩顶部扩散,随即1号墩墩底屈服,形成塑性铰并向墩顶发展,如图7。在不同地震动荷载组合作用下,墩底截面混凝土均出现开裂现象,在兰州波顺桥向作用下墩底截面部分钢筋进入屈服状态,屈服钢筋应力-应变曲线与墩底截面弯矩-曲率曲线分别如图8、9所示。
由图7可知1、2号墩塑性区发展程度不同,这与墩顶支座的约束有关,正确的模拟边界条件对动力弹塑性分析至关重要。由图9易看出墩底截面进入塑性阶段,且随着截面刚度衰减塑性发展程度逐渐加强。截面虽然进入塑性状态,但混凝土并无压碎,结构仍有一定的稳定性。
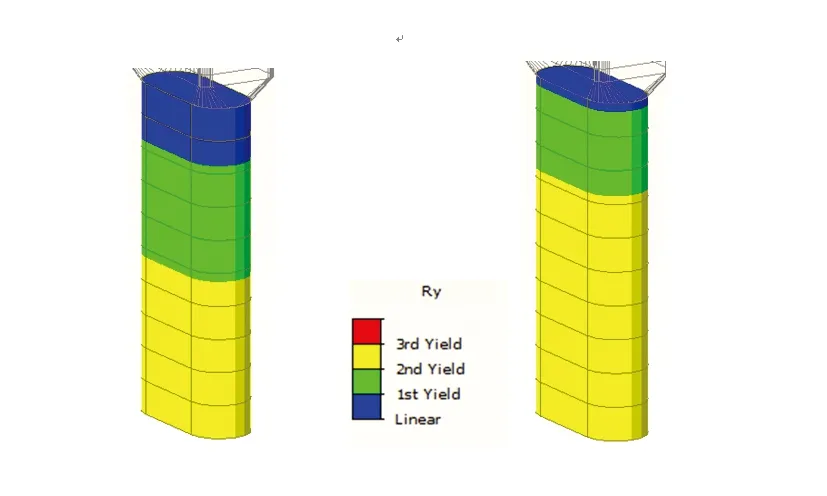
图7 兰州波顺桥向作用下1、2号墩塑性铰屈服状态
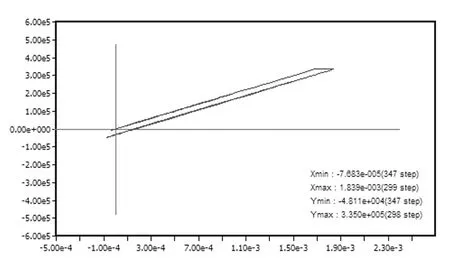
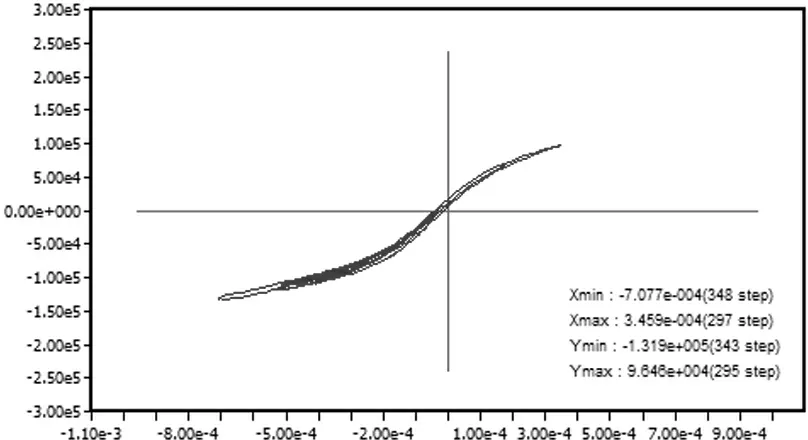
图8 钢筋单元应力应变曲线
图9 墩底单元My-Ry曲线
5.2 响应峰值
为了详细分析连续梁桥在罕遇地震作用下的动力反应,表6列出了1、2号桥墩在TAR_TARZANA波、芦山计生局波和兰州波不同荷载组合作用下桥墩墩顶位移、墩底剪力和墩底弯矩的地震响应峰值。
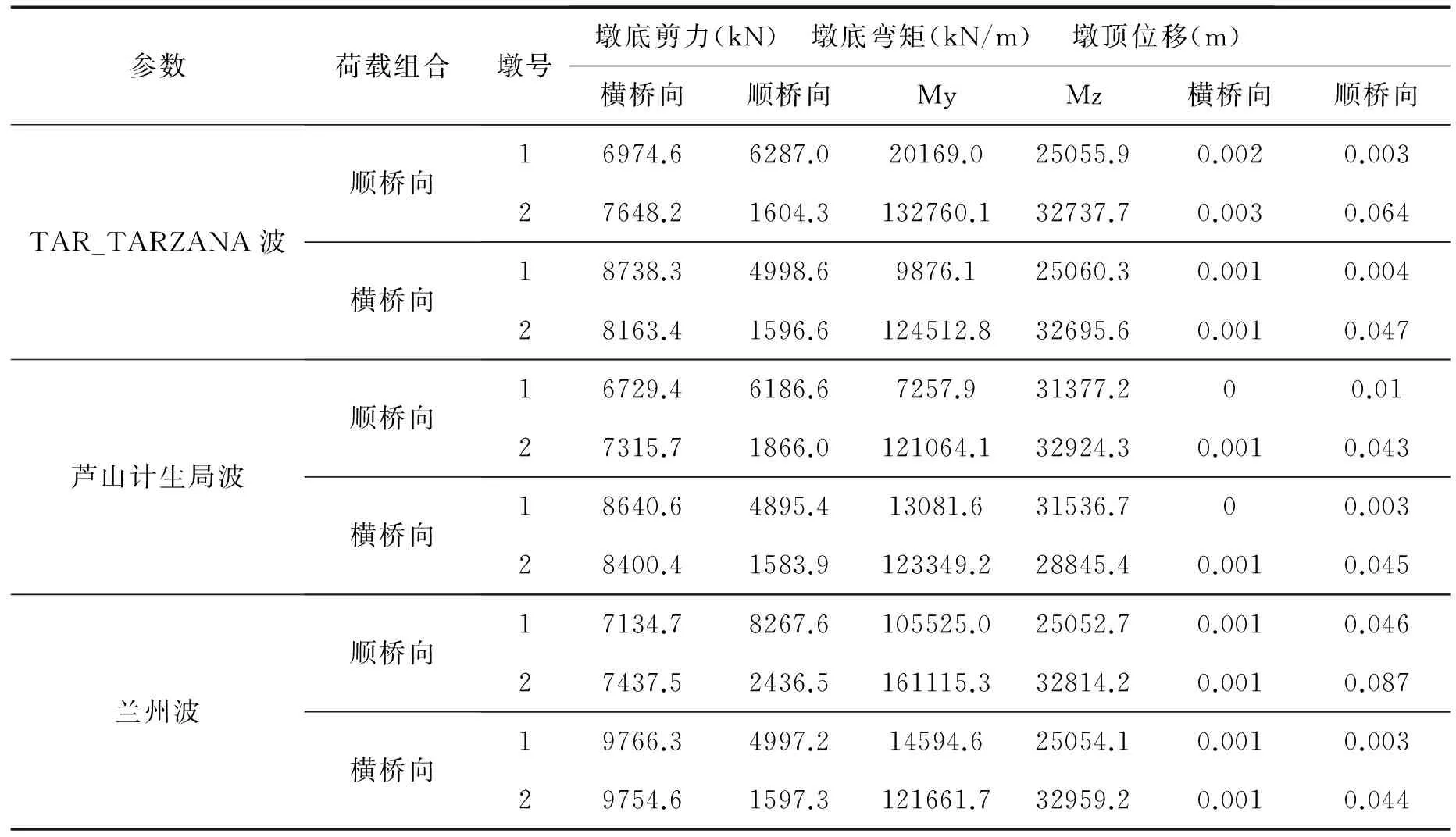
表6 响应峰值
由表6可以看出,在三条地震波六种荷载组合作用下,横桥向墩底剪力较大,最大值为9766.3 kN,作用在1号墩墩墩底;顺桥向墩底剪力较小,最小值为1583.9 kN,作用在2号墩墩底;My与Mz大小并无明显规律,但总体分析可知2号墩的弯矩大于1号墩,顺桥向位移相对较大,顺桥向荷载组合是最不利组合。
6 结论
运用有限元分析软件Midas Civil建立三跨连续梁桥有限元模型,分析其在罕遇地震作用下的动力响应,得出以下结论:
(1)对单桥和考虑轨道的两种全桥模型进行模态分析,结果表明全桥以低阶弯曲振动为主,考虑轨道模型的全桥自振周期相对较大,主要体现在低阶振型周期的增量变化,在进行抗震设计时考虑轨道的作用是有必要的。
(2)在罕遇地震作用下,连续梁桥墩底首先进入屈服阶段,形成塑性铰,并由底部向墩顶扩散,建议加密墩底箍筋。
[1] 叶慧. 2015年底中国高铁运营里程世界第一[EB/OL] [2016-01-14].http://www.rail-transit.com/SA_Detail.aspx?ID=216.
[2] XIA H, HAN Y, ZHANG N, et al. Dynamic analysis of a train-bridge system subjected to non-uniform seismic excitations[J]. Earthquake Engineering & Structural Dynamics,2006,(12): 1563-1579.
[3] 王少林,翟婉明.地震作用下高速列车-线路-桥梁系统动力响应[J].西南交通大学学报,2011(1): 56-62.
[4] 鞠彦忠,阎贵平,李永哲.低配筋铁路桥墩抗震性能的试验研究[J].铁道学报,2004(5):92-95.
[5] 李永哲. 钢筋混凝土桥墩弹塑性变形及塑性铰区特性研究[D].北京:北京交通大学,2004.
[6] 中华人民共和国住房和城乡建设部.GB50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社,2010.
[7] 中华人民共和国铁道部.GB50111-2006铁路工程抗震设计规范[S].北京:中国计划出版社,2009.
[8] 吕杨,徐龙河,李忠献,等.基于纤维模型的钢筋混凝土结构动力弹塑性分析[J].震害防御技术,2010(2):257-262.
[9] 胡聿贤. 地震工程学(第2版)[M].北京:地震出版社,2006.
[10] 王晓伟,叶爱君.大跨度斜拉桥地震反应分析谱分析中计算振型数研究[J]. 结构工程师,2011(4): 84-90.
(责任编辑:孙文彬)
Analysis of Dynamic Elastic-plastic Responses of High-speed Railway Bridge under Strong Earthquake
LIANG Sheng-jian
(Huai'an Traffic Holding Co., Ltd, Huai'an Jiangsu 223001, China)
In order to study the elastic-plastic responses of continuous girder bridge under strong earthquake, a finite element model of three-span continuous girder bridge was set up based on Midas Civil. Vibration characteristics of the model with rails and the model without rails were compared, and dynamic elastic-plastic responses of continuous girder bridge under different seismic load combinations were comparatively analyzed. The results show that the vibration characteristics of the two models with and without rails have obvious differences and the natural vibration period of the model with rails is longer, strong earthquake make the bottom of pier into the elastic plastic state, resulting in plastic hinge.
high-speed railway bridge; strong earthquake; vibration characteristic; elastic-plastic responses
2017-01-18
梁升建(1991-),男,山东聊城人,硕士,主要从事生命线工程抗震及工程项目管理研究。
U448.13
A
1009-7961(2017)03-0054-07

