弦支穹顶结构预应力优化设计方法综述
黄卫林,刘树堂
(广州大学土木工程学院,广州 510006)
弦支穹顶结构预应力优化设计方法综述
黄卫林,刘树堂
(广州大学土木工程学院,广州 510006)
最佳预应力是弦支穹顶设计的核心和关键问题。针对目前弦支穹顶结构没有统一的预应力设计方法,基于四种预应力设计准则总结了各类弦支穹顶结构预应力确定的方法。特别对于大跨度隔圈布索、椭圆弦支穹顶预应力设定的方法和步骤进行了阐述。评述了各类方法的优缺点及工程适用性,提出弦支穹顶最优预应力设计:必须考虑下部索杆布置优化、预应力值优化两个层次,为实际工程预应力设计提供参考依据和借鉴。
弦支穹顶结构;预应力优化;优化设计;布索优化
0 引言
弦支穹顶是单层网壳和索撑体系组合形成的大跨度预应力结构。预应力通过对上部单层球面网壳反向荷载有两个作用:① 降低上部单层网壳结构对周边构件的水平约束反力;② 降低撑杆内力峰值、控制结构的变形[1]。而过大的预应力,不仅不能改善结构的受力性能,而且会更加重了整个结构的负担、造成反向径向位移、施工难度明显增加。过小的预应力,不能完全表现其高效的结构优势和受力性能[2]。因此弦支穹顶结构设计的关键在于确定合适的预应力。由于弦支穹顶结构清晰的传力路径和结构造型的优势,一经提出就显示出广阔的应用和发展前景。目前弦支穹顶结构广泛用于大型的航站楼、综合体育场馆以及国际性会展中心等公共设施的屋盖中。标志性的工程有:聚会穹顶、2008奥运会羽毛球馆、济南奥体中心体育馆、常州体育馆等。
1 弦支穹顶结构预应力优化设计的研究现状
1.1 弦支穹顶结构预应力优化设计现状
确定弦支穹顶预应力大小的本质上就是预应力优化问题。而目前关于弦支穹顶结构优化设计的理论尚不完善,实际工程优化设计的经验也不足,特别是针对超大跨度实际工程的优化设计研究还属于空白[3]。弦支穹顶结构最优预应力设计需要考虑两个优化问题:一是下部索杆布置的优化;二是结构预应力的优化,这两个层次的优化是预应力分析的关键。文献 [4]指出弦支穹顶结构具有初始刚度、非线性特征不明显,可用线性叠加荷载的方法来分析受力。在弦支穹顶预应力设计研究方面:文献 [5]深入研究弦支穹顶屋盖选型、施工模拟、索杆体系的合理布置等关健性问题,探讨了预应力的大小确定的原则。董石麟等[6]以外荷载作用下各圈撑杆上节点Z向位移为零为原则,确定了各圈环索预应力的比值,为工程预应力比的确定提供参考。唐红等[7]提出了按预应力控制网壳变形的原则,对预应力进行设计。该方法具有简便实用,具有概念清晰,可应用于实际工程。除了设计准则之外,整个结构体系中构件的截面积、结构的构形的分布都是预应力设计的重要影响因数。
1.2 预应力设计的过程
值得注意的是索的预应力是在网壳的不同部位施加的,索力优化问题,目前还没有确定的方法。设计弦支结构预应力需要解决三个问题:①各圈索撑体系的整体自应力模态的确定;② 预应力分布的确定;③ 预应力水平的确定。对于第一个问题,利用应用关系及结构特定的形态可以简单确定。文献[8]采用ANSYS有限元软件分析了弦支穹顶结构的模态。陈志华等[9]以天津保税区商务中心为研究对象进行模态分析和地震响应研究,论述了预应力的设定理论;对于第二个、第三个问题也有大量文献进行了研究:文献 [10]指出确定合理预应力,需要引入弦支穹顶结构由于拉索预应力的三种状态:放样态、预应力平衡态、荷载态。最理想的结构状态是在预应力,自重以及荷载的共同作用下,结构的水平支座径向反力为零及撑杆的内力峰值最小。
1.3 预应力设计的基本方法
弦支穹顶结构预应力设计方法做了大量的研究:田国伟等[11]详细研究了弦支穹顶结构的预应力设计的方法,推导出计算撑杆预应力大小的具体公式,设定的环索预应力值较为可靠、准确。文献[12]将弦支穹顶结构的已有的预应力设方法总结为5种预应力设计、分析的方法:① 试算法 (要求经验);②基于力学平衡原理的简化公式 (计算量大);③ 局部分析法 (一定的精度);④ 遗传优化算法(应用不方便);⑤ ANSYS优化模块(有限元理论)。文献[13]基于力学原理提出了预应力设计公式,提出了加强外圈索力抵消水平位移。张明山等[14]提出的二级优化法采用遗传算法,迭代速度快,但每次只能优化单一目标,不能保证同时优化两级目标函数,陈志华等[15]详细研究了二阶段分析法预应力设计的计算理论,该方法可避免拉索松弛,从而清晰的反映了在荷载作用下杆件内力变化。
2 不同准则下预应力的优化设计
不同的拉索预应力设计准则,所得到的预应力水平以及预应力分布是不同的。所以预应力的设计准则可以作为预应力优化设计的一种方式。
2.1 基于等效节点荷载准则下预应力设计
基于等效节点荷载准则:各环索位置的撑杆轴压力与单层网壳上等效节点力相平衡以及减少最外环杆件对支座的水平推力为原则,亦称几何法[16]。几何法确定预应力的过程如下:
(1)环索预应力比确定:
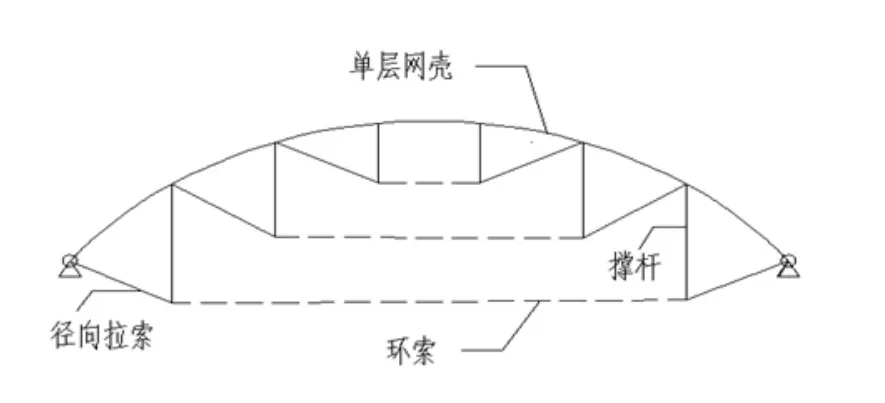
图1 弦支穹顶结构剖面图Fig.1 Sectional view of the suspen-dome structure
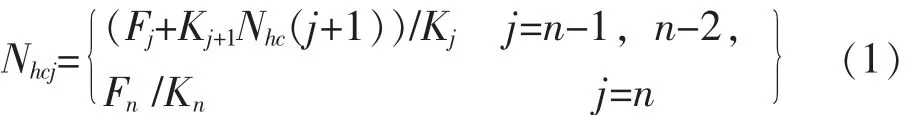
(2)确定预应力水平的方法:
如果单层网壳各等效节点荷载 已知,则根据公式可以得到的数值。这个值就是预应力平衡态的数值也是工程实际施加的预应力值。单层网壳的等效荷载可有节点所属的面积确定。由上述几何关系可以确定各圈预应力比和预应力。
该方法概念清晰,逻辑性推理性强,在实际工程的应用中具有普遍的意义。但几何法面临不得不面临3个问题:① 假定各圈水平投影的夹角相等,因实际结构水平投影夹角不等而造成计算误差。② 假定各圈水平投影的夹角不同,则重复计算各圈的平衡方程,计算量太大。③ 没有考虑内力的重分布,使得结构的位移和内力分布很不均匀;预应力结果需要张力补偿法再处理[17]。特别对于跨度大、间隔布置的结构甚至有些假定不可能得到满足。
2.2 基于初始建筑构形准则下预应力设计
基于初始建筑构形的准则[18]指出:在结构安装就位完成时的结构构形达到建筑设计规定的结构构形,该准则使得预应力分布的确定更为简便。
(1)预应力水平确定。
文献[19]推导荷载态结构端拉索设计预应力计算公式和位移表达式,满足风吸效应下环索不出现压力,不松弛。实际以预应力状态下结构中点的反拱位移公式与荷载状态下垂直位移公式相等导出的计算公式为准。
假设条件:① 完全刚性结构的上部的单层网壳;②单层网壳反向加载系统为下部的张拉体系;③预应力通过环索施加其中公式(1)中:
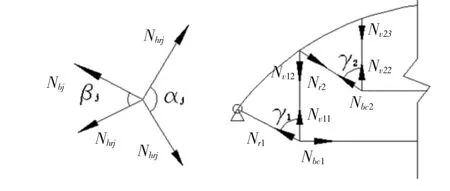
图2 预应力比值计算模型Fig.2 Prestressed ratio calculation model
(2)环索预应力比确定。
文献[20]研究了一种简单确定环索预应力分布的方法,如:假定第i圈环索范围内单层网壳荷载与第i到i+1环索之间上方内侧二分之一的网壳宽度荷载总和等于第i环撑杆总等效压力P(从内到外编号)。那么第i环每根撑杆的等效压力为P/n(其中n为该环撑杆的根数),各环索内力可利用下部索撑体系的平衡方程求解,最终求得预应力的比值。需要考虑结构的自重、屋面活载、恒载的作用来计算各圈撑杆等效压力P值。与几何法对比,该的方法思路简单、概念清晰以及方便使用,不需要做各圈的水平投影夹角相等以及不同环索处等效节点荷载大小相等的假设,能达到规程方法的优化程度。
2.3 基于水平支座反力的最小准则下预应力设计
基于水平支座反力最小的准则。而控制水平径向反力与控制水平径向位移本质上相同,该预应力设计准则研究最为广泛。
2.3.1 二级优化法预应力设计
弦支穹顶结构预应力优化设计方法之一的二级优化法采用了遗传算法。该方法设置了两个目标函数,第一个目标函数:即先以对周边构件的支座反力最小化为目标,确定下部各圈索杆径向斜索的预应力值,并将其求和得T。第二个目标函数:当预应力水平总和T确定后,以单层网壳杆件的最小轴向内力为目标,在各圈预应力水平总和T不变的基础上每圈索杆预应力进行重分布。如上所述采用二级优化求解策略,根据预应力重分布结果,调整的取值范围,直到得到预应力水平和预应力分布的合理取值为止[21]。二级优化法最大的特点就是两个目标函数在预应力优化过程中可能是矛盾的需要进行协调和折衷处理。
2.3.2 自平衡逐圈法确定预应力设计
自平衡逐圈确定预应力的方法是一动态控制预应力的新方法。其基本理论为:弦支穹顶结构体系的自平衡性和按内圈到外圈的顺序逐圈分析。
求解思路:假设荷载q作用下的弦支穹顶布置了3圈环索。在荷载q作用下,由内圈向外圈求解,根据结构自平衡的特点,子结构SS-1的水平径向反力H1,可确定内圈拉索的预应力P1。子结构SS-2(包括内圈和中圈两道索系)的水平径向反力H2由内圈和中圈拉索共同承担。P1以已确定,中圈预应力P2可确定,子结构SS-3在荷载q作用下产生的水平反力H3,而P1、P2已知,外圈预应力P3亦能确定,竖向反力V1、V2向外圈传递。V3由支座传递受力。至此,确定了环索预应水平及分布(3圈)。
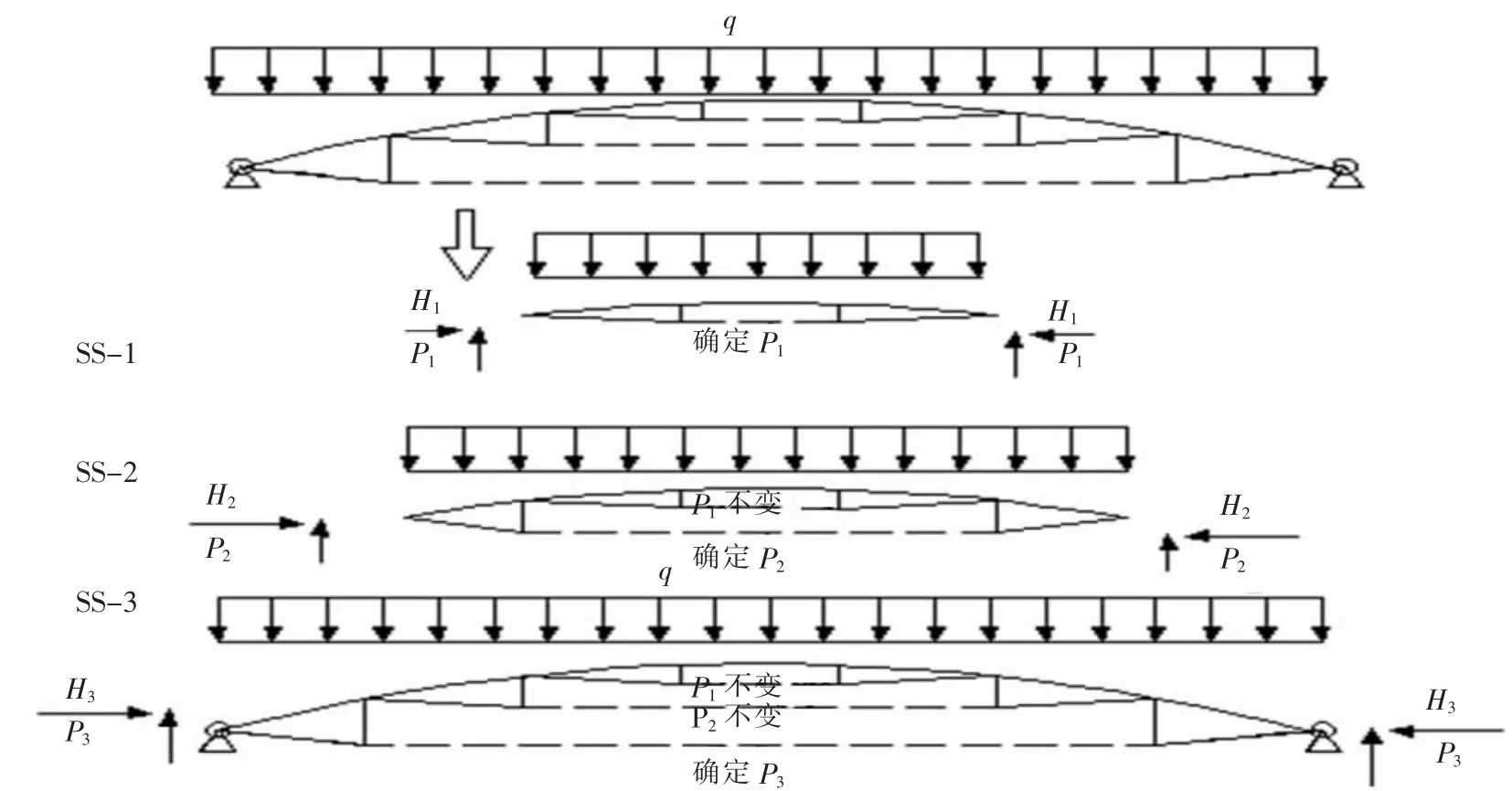
图3 自平衡体系求解图Fig.3 The solving graph for self-balancing system
自平衡逐圈确定法[22]最大的特点确定各圈环索预应力比由各圈的预应力值来确定。各圈拉索预应力是逐步求得的,而非同时确定。该方法预应力的确定必须是内圈到外圈的顺序,只有求解出内圈拉索预应力,才能获得外一圈拉索的预应力。求解预应力时必须进行内力分析,是一种动态控制预应力设计的方法。自平衡逐圈确定法概念明确、应用方便,既适用于椭圆形弦支穹顶,也适用于圆形弦支穹顶;所确定的预应力数值合理可行,能显著改善整体结构的受力性能。
2.3.3 刚性索法预应力设计
刚性索法预应力设计基本原理为:首先在有限元软件中建模,其次放大100倍索的弹性模量,设初应变为0,采用ANSYS作静力分析,得到预应力值,最后采用张力补偿法解决预应力损失等问题[23]。然后根据计算结果确定各圈预应力值和预应力比。
刚性索法考虑预应力是重分布,杆件受力均匀,预应力分布相对合理,弦支穹顶在跨度很大、间隔布索时,几何法不可用,可采用刚性索法。但采用刚性索法进行预应力设计的不足之处是:内部几圈索力较小,构件受力不均匀。加大局部节点荷载可改善这个缺点。局部调整的环索预应力可更好的控制内圈的节点位移,降低结构的变形。
2.3.4 基于平衡矩阵理论和最优化理论的预应力确定方法
(1)预应力水平确定。基于平衡矩阵理论的自应力模态和机构位移模态以及整体可行预应力理论确定弦支穹顶结构预应力。对于联方型弦支穹顶,整体可行预应力向量解是唯一的。
(2)预应力分布确定。弦支穹顶结构预应力分布由最优化理论确定。即在整体可行预应力确定后,预应力设计变量转化为预应力水平系数U值,求出预应力和预应力比。文献[24]利用最优化理论来确定各环之间预应力水平组合因子。基于力学平衡原理的简化公式的设计方法较试算法效率提高了很多,但该方法计算量较大。
2.3.5 整体预应力设计
(1)预应力水平的确定。确定整体预应力水平具体做法是:①环索索力为零,得不同荷载下支座水平位移-荷载图;②零外荷载时,得不同预应力水平下支座水平位移-荷载图;③基于实际节点荷载,双线性插值求解,该值为最优的水平[25]。该方法概念清晰,计算简单,但对于各圈相邻节点荷载不同的结构,得先处理才能计算。
(2)环索预应力分布的确定。确定整体预应力水平后,切向平衡法[26]确定各圈预应力比例,该方法可避免网壳 “外凸”,降低预应力损失。文献[27]指出当单层网壳层各节点所围合的空间在水平面上的投影面积非常接近时,预应力比值可设为n:n-1:n-2:…:1(由内向外编号)。文献[28]详细阐述了环索预应力比和预应力的确定方法,为预应力比值的工程应用提供参考,但参考的预应力比值不一定得到最优的预应力。
2.4 基于风吸效应环索松弛准则下预应力设计[29]
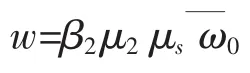
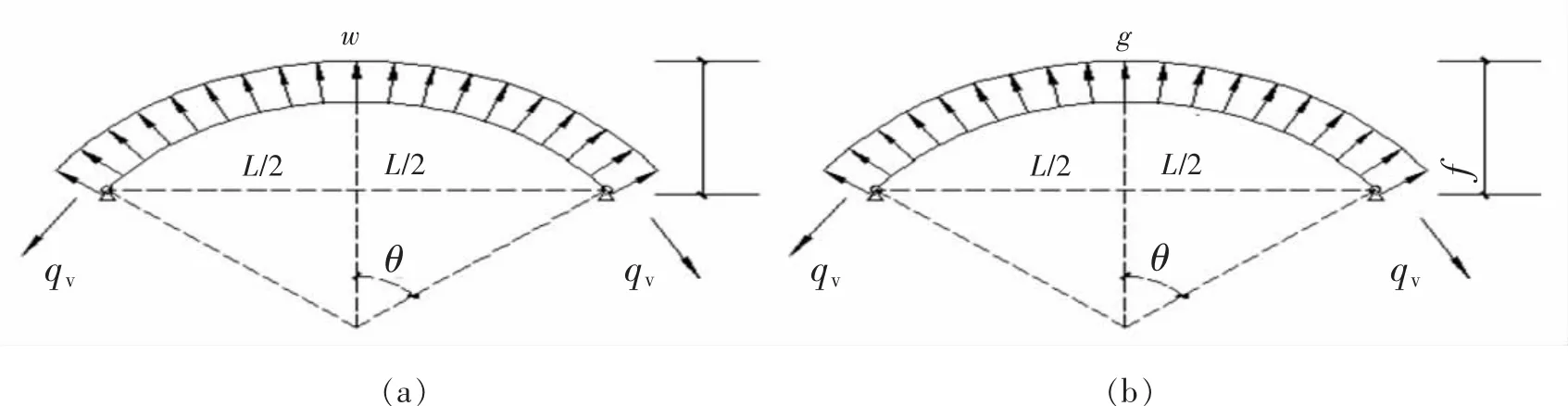
图4 均布风吸效应 (a)、自重效应 (b)Fig.4 Uniform air suction effect(a),deadweight effect(b)
求解公式如下:
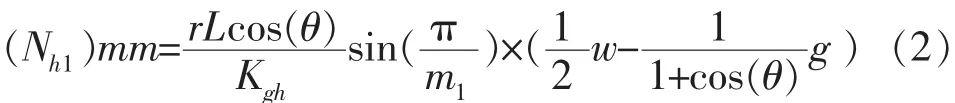
公式 (2)计算结果小于零则满足环索手拉状态,此时弦支穹顶整体的环索预应力已确定。弦支穹顶在风吸力作用研究方面:弦支穹顶结构中风荷载常常起主要甚至决定性作用。崔晓强等[31]指出风动效应强于地震作用。可见该结构为风敏感结构体系,对其预应力设计时必须考虑,否则该结构会失去预应力高性能的特性,必须保证环索不松弛,索内不出现压力,保证环索受拉特性。
3 下部索杆布置优化设计
弦支穹顶索杆体系的主要作用:一是减小结构对支座的水平推力,二是增大结构的稳定性能。索杆布置越多,整体稳定性越高,可见结构的稳定性与下部索杆中撑杆的布置数量与位置有较大的关系[25]。此外,下部索杆体系满布,并不能最好地改善结构的受力性能,应合理下部布置索杆体系。文献[27]指出:下部索杆的布置大大减小了上部网壳各环向、径向杆件轴力值,而且距离支座越近,轴力降低效果越明显。下部索撑体系圈数越多,结构各项性能的改善越明显。在索杆布置确定后,斜索的布置方式对结构的各项性能影响不大,撑杆高度对结构性能影响较大。结合施工难度与用钢量两方面,得出斜索的布置方式应以简单、实用即可,撑杆高度应取合理高度。总之,下部索杆体系的布置需要考虑结构受力性能与建筑功能、美观两方面考虑。首先从结构优化理论的角度分析,下部索撑体系的设置属于结构布局优化的范畴,而目前理论水平的限制,使得布索优化的建立数学模型进行优化布置还是相当困难的[22]。文献[32]研究了11种下部索杆布置对弦支弯顶结构静力性能与自振特性影响,为实际工程结构索杆布置的方式提供理论依据与参考。对于大跨度、间隔布索和撑杆的弦支穹顶分析时,文献[16]推导的预应力设定方法来确定预应力的方法将不再适用,无法控制上弦节点位移。可见下部索杆布置优化是弦支穹顶预应力设计时必须考虑的,其不仅对结构的静力、稳定性等各项受力性能的有较大影响,而且对预应力的确定也是直接影响的,显然弦支穹顶最优预应力的确定必须考虑下部索杆布置优化、预应力值优化两个层次。
4 结语
弦支穹顶预应力设计的方法目前还没有统一的确定方法,特别是对于大跨度、隔圈、椭圆弦支穹顶可参考的依据更少。
各类确定方法都有优缺点:几何法进行预应力设计,具有实用的意义,但不适用于跨度较大、隔圈布索的弦支穹顶结构,刚性索法由于考虑了结构内力重分布,使得预应力分布更均匀。通过局部加大内圈节点荷载的方法可更好的控制结构的变形。自平衡逐圈确定法适用于椭圆形、圆形弦支穹顶,该方法概念明确、应用方便,可以动态控制设计预应力。
弦支穹顶最优预应力的确定必须考虑下部索杆布置优化、预应力值优化两个层次。目前该结构预应力确定的方法较多的仅考虑预应力的优化,忽略了预应力和与结构布置的相互影响,以后可提出该方向确定预应力的相关理论,为工程提供参考。
[1]陈志华,刘红波,王小盾,等.弦支穹顶结构研究综述[J].建筑结构学报,2010(S1):210-215.
[2]郭佳民.弦支穹顶结构的理论分析与试验研究[D].杭州:浙江大学,2008.
[3]张爱林,刘学春.奥运羽毛球馆张弦穹顶基于整体稳定的优化设计[J].建筑结构,2007,02:1-5+26.
[4]K C,KANG W J,LAM H F,et al.Factors affecting the design and construction of lamella suspen-dome systems[J].J Constr Ste Res,2005,61(6):.
[5]姚 姝,范峰.K6型弦支穹顶结构的静力性能分析[J].建筑结构,2008(02):24-28
[6]董石麟,袁行飞,郭佳民,等.济南奥体中心体育馆弦支穹顶结构分析与试验研究[J].天津大学,2009:6.
[7]唐 红,蔡元奇.张弦式网壳结构中的拉索预应力值设计方法的应用研究[J].武汉大学学报(工学版),2006,02:119-122.
[8]YUAN X F,DONG S L.Nonlinear analysis and optimum design of cable domes[J].Eng Struct,2002,24(7):965-977.
[9]陈志华,张立平,李 阳,等.弦支穹顶结构实物动力特性研究[J].工程力学,2007,03:131-137.
[10]张国发.弦支穹顶结构施工控制理论分析与试验研究[D].杭州:浙江大学,2009.
[11]田国伟,刘金鹏,刘兴业,等.弦支穹顶结构中预应力的设定原则[A].天津大学建筑工程学院,2002:3.
[12]陈志华,刘红波,牛犇.弦支穹顶结构的工程应用[J].工业建筑,2010,08:42-48.
[13]KANG W J,CHEN Z H,HENG F L,et al.Analysis and design of the general and outmost-ringstiffed suspen-dome structures[J].Eng Struct,2003,25(13):1 685-1 695.
[14]张明山,包红泽,张志宏,等.弦支穹顶结构的预应力优化设计[J].空间结构,2004,03:26-30.
[15]陈志华,李 阳,康文江.联方型弦支穹顶研究[J].土木工程学报,2005,05:34-40.
[16]中国工程建筑标准化协会,预应力钢结构技术规程:CECS 2122006[S].北京:中国计划出版社,2006
[17]陈向荣,李小利,李海龙,等.联方凯威特型弦支穹顶结构预应力设定的探讨[J].四川建筑科学研究,2013,05:16-19.
[18]刘树堂.弦支穹顶结构尺寸优化设计的研究[J].建筑钢结构进展,2012,06:38-46.
[19]刘树堂.大跨张弦桁架结构尺寸优化设计研究[J].河南大学学报(自然科学版),2014,02:244-247.
[20]刘树堂.张弦桁架结构拉索设计预应力影响因素研究[J].广州大学学报(自然科学版),2011,06:62-67.
[21]刘谦.弦支穹顶结构的预应力优化设计[J].四川建材,2006,01:157-160.
[22]石开荣,郭正兴,罗 斌.椭圆形弦支穹顶结构的预应力确定方法研究[J].土木工程学报,2010,09:88-99.
[23]杨 波,戴国欣,聂诗东,等.倒圆角三角形弦支穹顶结构预应力优化[J].建筑结构,2010,05:100-103.
[24]张志宏,张明山,董石麟.平衡矩阵理论的探讨及一索杆梁杂交空间结构的静力和稳定性分析[J].工程力学,2005,06:7-14+20.
[25]刘学春.新型大跨度弦支穹顶结构体系创新研究与奥运工程应用[D].北京:北京工业大学,2010.
[26]付智强,高博青,张 瑞.弦支穹顶结构预应力设定方法探讨[J].天津:天津大学,2009:6.
[27]陈志华,冯振昌,秦亚丽,等.弦支穹顶静力性能的理论分析及实物加载试验[J].天津大学学报,2006,08:944-950.
[28]蔡建国,冯 健,涂展麒,等.弦支穹顶结构预应力设计及其抗震性能研究[J].四川大学学报(工程科学版),2009,04:70-75.
[29]CAO Q S,ZHANG Z Z.A simplified strategy for force finding analysis of suspen-domes[J].Eng Struct,2009,321.
[30] KANG W J.Analysis and design of the general and outmost-ringstiffed suspen-dome structures[J].Eng Struct,2003,25:13.
[31]崔晓强,郭彦林.弦支穹顶结构的抗震性能研究[J].地震工程与工程振动,2005,01:67-75.
[32]郭佳民.弦支穹顶结构的理论分析与试验研究[D].杭州:浙江大学,2008.
A Summary of Optimization Method of Prestressed Suspen-dome Structure
HUANG Weilin,LIU Shutang
(School of Civil Engineering,Guangzhou University,Guangzhou 510006,China)
The optimal prestress is the core and key problem of the design of string-supported dome.There is no unified design method of prestressing force for the current suspen-dome structure.Based on the four prestress design criteria,this paper summarizes the methods to determine the prestress of various suspender dome structures.In particular,the methods and steps of setting the prestressed force of large-span spacer cable and elliptical suspen-dome are described.The advantages and disadvantages of each method and the applicability of the method are discussed.The optimal prestress design of suspender dome is put forward:the lower strut layout optimization and the prestress value optimization two levels must be considered,which can provide reference for practical engineering prestress design.
Suspen-dome structure; Prestressoptimization; Optimization design; Tendon disposition optimization
TU399
:A
:1001-8662(2017)01-0029-06
10.13512/j.hndz.2017.01.005
黄卫林,刘树堂.弦支穹顶结构预应力优化设计方法综述[J].华南地震,2017,37(1):29-34.[HUANG Weilin,LIU Shutang.A Summary of Optimization Method of Prestressed Suspen-dome Structure[J].South china journal of seismology,2017,37(1):29-34.]
2016-05-26
黄卫林 (19-)
E-mail:1273448126@qq.com.

