错在哪里

数学园地

错在哪里

1 江苏省海州高级中学

冯善状(邮编：222023)

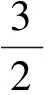
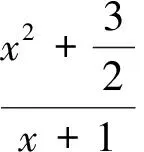
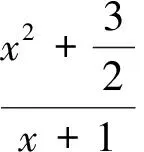
2 新疆生产建设兵团第二中学

张国治(邮编：830002)

甘肃省渭源县第三中学

兰建军(邮编：748200)

题目(金太阳教育研究院2017年《小题大做》第22页高考仿真卷九第11题)

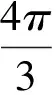
解析(该资料提供的标准解答)

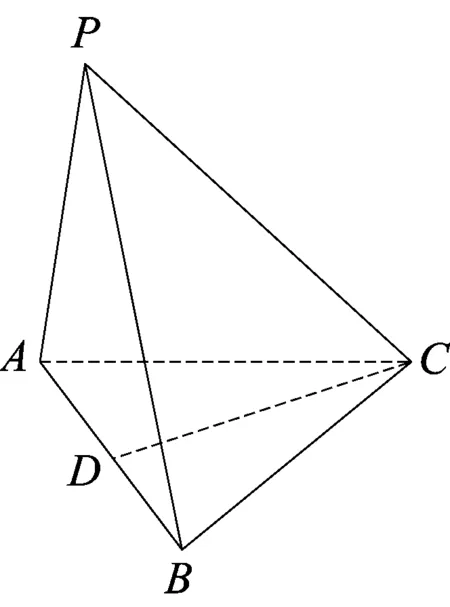
图1

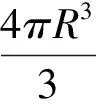
题目错了，错在哪里？

上述题目及解答似乎无懈可击，但却犯了一个致命的错误，即符合题意的四面体P-ABC是否存在？此题的作者在编拟试题时有心理上的“潜在假设”，即认为符合题意的四面体是存在的，但是本题中的四面体P-ABC并不存在，从而此题根本上是一个错题.

错误剖析1：

图2

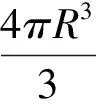
错误剖析2六正数如何能构成四面体六棱长？为此查询期刊，《六正数构成四面体六棱长的充要条件》一文(以下简称文[1])中给出如下结论：

图3

设a、a′、b、b′、c、c′为六个正数，则这六个正数构成四面体的充要条件是：F(a,a′,b,b′,c,c′)=a2a′2(b2+b′2+c2+c′2-a2-a′2)+b2b′2(c2+c′2+a2+c′2-b2-b′2)+c2c′2(a2+a′2+b2+b′2-c2-c′2)-(a2b2c2+a2b′2c′2+a′2b2c′2+a′2b′2c2)>0(其中a、a′;b、b′;c、c′各为四面体的一组对棱，如图3).

若将题目作如下修正，则不失为一道训练学生思维能力的一道好题.

试题修正：

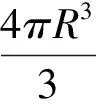
说明如图4，设球O的半径为R，若符合题意的四面体P-ABC存在等价于则四面体O-ABC必存在，由文[1]的结论可知，F(R,1,1,

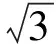
可见，对于题目的编制应遵循条件相容性原则，即题设条件之间不能互相矛盾.

此题较明显的错误是底面积的前后不同.事实上，通过正本清源发现更本质的错误在于根本忽视了六正数如何能构成四面体六棱长这一隐含条件.

总之，试题编拟过程中题目的条件对于推出结论是充分的，而有些条件不充分的题目，之所以存在，是由于编拟试题和解题时有心理上的“潜在假设”，或逻辑上的“以偏概全”.当然，在试题编拟过程中要特别注意隐含条件，题设条件不能与本系统的公理、定理、已知正确的结论等相矛盾，而且题设中的多个条件之间也不能互相矛盾.当然，解题环节中也需要“常回头看看”，养成良好的检查习惯.