一个不等式的应用举隅
2017-07-24 13:40:45安徽省霍邱县第一中学邮编237400
中学数学教学 2017年3期
安徽省霍邱县第一中学 (邮编:237400)
一个不等式的应用举隅
安徽省霍邱县第一中学冯克永(邮编:237400)
不等式ex≥x+1
(1)
(其中e=2.71828…是自然对数的底数(下同))等号当且仅当x=0时成立.
(来源:人教A版选修2-2第32页B组第1题第3小题:ex>x+1,x≠0).
证明作差构造函数f(x)=ex-x-1,则f′(x)=ex-1,由f′(x)=0得x=0.当x∈(-,0)时,f′(x)<0,当x∈(0,+)时,f′(x)>0.所以f(x)≥f(0),即ex≥x+1,等号当且仅当x=0时成立.
当x+1>0时,对不等式(1)两边取自然对数得ln(x+1)≤x,
(2)
等号当且仅当x=0时成立.
笔者经过研究发现,应用不等式(1)及其变形(2)可简便地证明含有ef(x),lnf(x)的不等式.
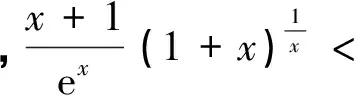
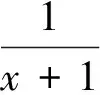
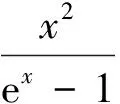

点评不等式是深刻认识函数的重要工具,二者结合是近几年高考命题的新热点.第(1)小题是常规的导数题易解决,第(2)小题利用常见不等式ex≥x+1及加法运算化整体为局部,再利用第(1)小题的结论,取a=2放缩传递是神来之笔,很值得回味.试题命制一般遵循设问之间的连贯性,在后问“山穷水尽”之时,前问(有时即使未解决,用其结论也可以)往往会带来“柳暗花明”之喜,这应引起我们的高度重视.
2017-03-19)
猜你喜欢
中学生理科应试(2024年3期)2024-06-26 07:54:45
初中生世界·七年级(2022年6期)2022-05-28 14:02:01
现代畜牧科技(2021年10期)2021-11-19 08:42:30
中国篆刻·书画教育(2019年9期)2019-12-02 13:49:27
中国篆刻·书画教育(2019年9期)2019-12-02 13:49:27
中学数学研究(广东)(2018年24期)2018-03-12 00:43:44
中国篆刻·书画教育(2018年2期)2018-03-07 18:05:47
高中数理化(2016年5期)2016-09-26 06:48:04
新闻传播(2016年1期)2016-07-12 09:24:51
中学生数理化·高二版(2016年2期)2016-05-30 07:50:39

