“五四模型”的火焰燃烧稳定性判定
陈荣保,曹子沛,肖本贤
(合肥工业大学电气与自动化工程学院,安徽 合肥 230009)
“五四模型”的火焰燃烧稳定性判定
陈荣保,曹子沛,肖本贤
(合肥工业大学电气与自动化工程学院,安徽 合肥 230009)
燃烧稳定性判定问题是锅炉燃烧状态自动监测中亟待解决的关键问题之一。为了实现自动化监测,并对燃烧的稳定程度进行量化判定,基于数字图像处理技术,从炉腔火焰图像中提取燃烧参数,建立燃烧参数数据库。基于多属性判定方法,生成区间数据样本决策库。在模糊推理中,为获取隶属度函数参数和模糊推理规则,提出了基于粗糙集简化样本决策库。按照决策属性离散化决策库中的条件属性,实现了属性简约和属性值简约,增加了网络训练样本参数的可靠性。结合模糊网络的逻辑推理性和神经网络的学习性、并行计算等优点,建立了用于燃烧诊断的T-S模糊神经网络模型。选择合适的模糊分割数,定义“五四模型”,建立基于“五四模型”的火焰燃烧稳定性判定模型,并进行仿真试验。对比训练前后的仿真图参数表明,该模型是可行的,并具有较好的试验效果。
燃烧稳定性; 火焰图像处理; 样本决策库; 隶属度函数; 粗糙集; 离散化; T-S模糊神经网络; 分割数; 五四模型
0 引言
火力发电是我国电力生产的主要方式。对于大型燃煤锅炉而言,燃烧的不稳定既不环保节能,又不安全可靠[1]。燃烧火焰是燃烧状态的最直接反映[2],目前大型电站锅炉所使用的火焰图像检测系统还需要人工现场观察,因此火焰图像燃烧稳定性判定一直都是锅炉自动监测中亟待解决的问题之一。科学地解决该问题对实现锅炉自动监测和安全运行具有实际意义[3]。
燃烧过程是一个剧烈变化的过程,为克服燃烧杂质带来的噪声影响[4],需要建立一个具有较好的泛化和容错能力的燃烧稳定性判定模型。模糊神经网络模型能够满足上述要求[5]。因此,本文提出基于Tagaki-Sugeno模糊神经网络的燃烧稳定性判定模型,建立“五四模型”,实现燃烧稳定性判定。
1 燃烧特性及样本参数选取
1.1 火焰图像的预处理
对燃烧特性进行分析是确定火焰图像监测算法的关键步骤,火焰图像可能受到了外界的干扰[6]。为了得到更加清晰、更加趋于现实的火焰特性,更是为了得到更加准确的火焰图像燃烧参数,本文需要对样本图像进行预处理。采用的预处理方法为文献[7]中所阐述的灰度化和中值滤波。
灰度化是将彩色图像作灰度处理,转化为灰度图像。根据RGB颜色空间与YUV颜色空间的对应变换关系,建立亮度Y与R(红)、G(绿)、B(蓝)颜色分量的对应关系Y=0.3R+0.59G+0.11B,计算各个像素点的亮度值Y,并将该亮度值信息作为灰度图像的灰度值。
中值滤波能够滤除火焰图像中的随机噪声,并且因其非线性特点,不对阶跃信号造成影响,从而不会造成图像模糊。中值滤波的数字表达式如式(1)所示。
g(x,y)=med{f(x-i,y-i)}i,j∈S
(1)
式中:g(x,y)、f(x,y)为图像数据矩阵的像素灰度值;S为滑动窗口范围。
1.2 燃烧样本参数的选取
采样摄像头摆放位置不佳,导致火焰图像圆形度不够理想。文献[7]~ 文献[11]采用火焰平均灰度、有效区平均灰度、高温区面积、圆形度、火焰质心偏移、火焰丰度等样本燃烧参数。综合考虑,本文选取火焰平均灰度、有效区平均灰度、火焰丰度、高温区面积率、质心偏移作为燃烧参数进行研究。这五个参数均是对火焰图像进行预处理后提取得到的。
火焰平均灰度表述了火焰能量高低和火焰辐射平均光强。在稳定燃烧的情况下,火焰脉动并不强烈,图像平均灰度波动变化较小;在不稳定燃烧的情况下,不稳定燃烧时火焰的剧烈脉动,图像平均灰度变化波动比较大。
火焰丰度,即火焰有效面积,表示火焰图像中火焰面积占整幅图像的比例,反映火焰的占满程度。由于炉腔内的环境因素,会引起火焰图像的波动,灰度值的变化和火焰有效面积的波动是脉动特性在图像上最为明显的表现。
高温面积率反映火焰完全燃烧区占火焰图像的面积。在火焰完全燃烧区内,煤粉燃烧充分,燃烧脉动和火焰面积波动剧烈,温度也是最高的。此高温区面积的变化最能反映炉腔内火焰燃烧稳定性。
质心偏移距离指的是火焰高温区的切圆质心与基准状态的质心偏移的距离。随着炉膛内煤粉投入状况和一、二次风量的变化,火焰运动是必然的,用图像中的火焰质心偏移来表示火焰的中心位置变化。如果炉膛内各燃烧器配风不当或个别燃烧器工作不正常,会造成火焰中心偏移和变形。
由于煤粉火焰脉动频率为10~30 Hz,火焰中心脉动频率为5~10 Hz[9]。为消除火焰脉动对燃烧稳定性判定的影响,对火焰视频的每5帧图像的火焰参数取最大值、最小值以及平均值,得到参数样本。这样每组样本数据至少包含一个火焰脉动,以此得到燃烧参数数据库。
2 基于模糊神经网络燃烧稳建模
基于T-S模型的燃烧稳定性判定结构图如图1所示。
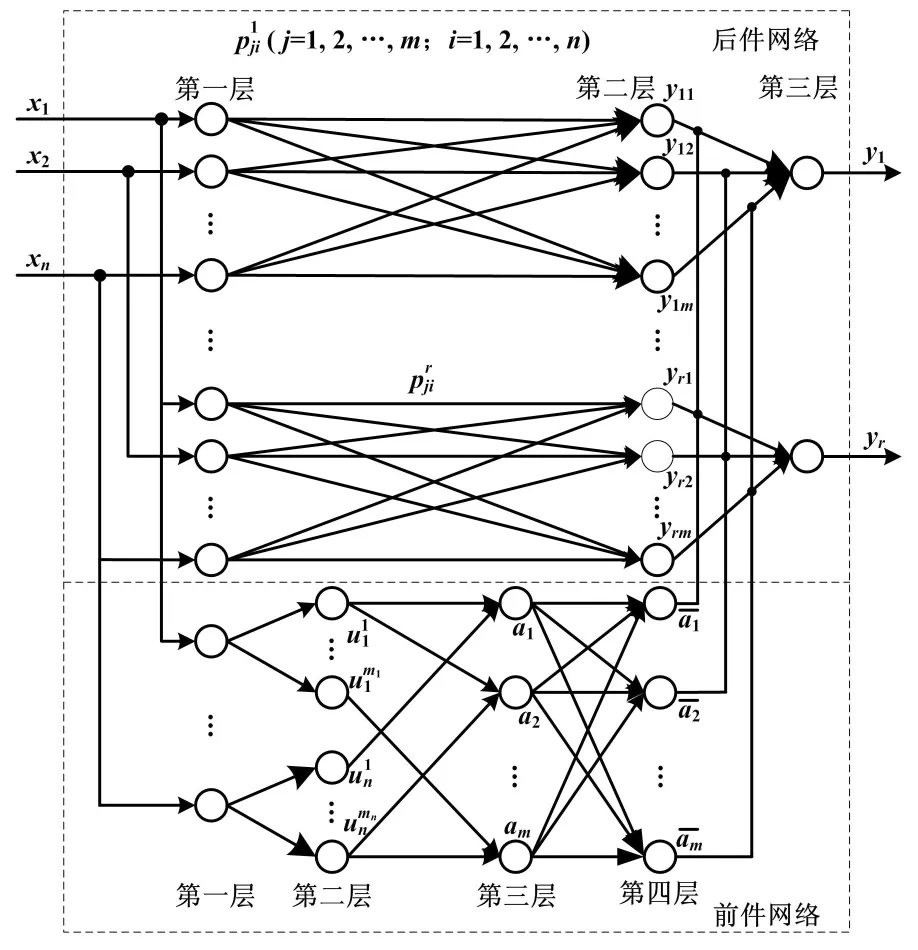
图1 基于T-S模型的燃烧稳定性判定结构图
图1中:网络结构分为前件网络与后件网络,匹配模糊规则的是前件网络[12];后件网络则用于产生模糊规则,确认模型最终输出结果。
神经网络输出的是燃烧稳定性,故本文构造的是MISO网络模型,有5个输入和1个输出。
前件网络组成结构为4层[13],如图1所示,第一层是输入层,它的各个节点直接和输入向量的各个分量xi连接,它起着将输入值x=[x1,x2,…,xN1]T传送到下一层的作用。该层的节点数N1取5。
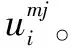
第三层是规则层,每个节点代表对应的模糊规则,它的作用是匹配模糊规则的前件,计算每条规则的适用度,如式(2)所示。
(2)
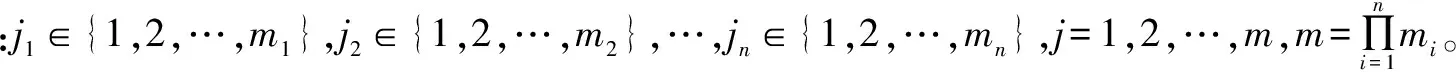
第四层是归一化计算,如式(3)所示,节点数N4=N3=m。
(3)
后件网络由γ个结构相同的并列子网络组成,每个子网络有一个输出量[14]。第一层为输入层,作用是传递输入变量到第二层。第二层有m个节点,节点分别代表着相应的规则,该层的作用会计算各个规则的后件。基于T-S模型的模糊神经网络分一阶线性网络模型和零阶网络模型,这里选用零阶网络模型,对稳定性输出进行定义:yi=k,k为稳定度。第三层是对系统输出进行计算,如式(4)所示。
(4)
由上式可得,各规则后件的加权和是yi,各个规则归一化后的适用度是其加权系数,也就是把前件网络的输出用作后件网络第三层的连接权值。
3 T-S模糊隶属度函数和规则获取
3.1 燃烧决策库生成
基于模糊神经网络燃烧稳定性判定燃烧规则及燃烧训练参数的选取,对燃烧稳定性判定有着重要的作用。如何选取有效的模糊推理规则和训练参数成为模糊神经网络燃烧稳定性判定不可回避的问题。本文就此问题,提出基于样本决策表提取规则库和训练样本。为了得到有效的样本数据库,本文选用文献[10]的基于区间数的多属性判定思想获取燃烧决策库,选定一组燃烧图像,组成样本集IS={S1,S2,…,Sn},并将其表示为一个四元组的信息系统IS=(S,A,V,f),A是非空有限属性集,A=C∪d={火焰平均灰度、有效区平均灰度、火焰丰度、高温区面积率、质心偏移,稳定性},C={c1,c2,c3,c4,c5}为条件属性,d为决策属性,V为属性值的集合,f→S×A表示条件属性映射的属性值集合。
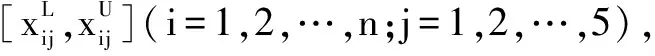
3.2 隶属度函数及燃烧规则库
由3.1节生成了样本决策表,但是决策表中样本燃烧参数是区间数,使得样本参数不能被直接处理,需要对其作离散化处理。离散化是为了实现规则提取和模糊初始隶属度函数参数的获取。本文选取文献[8]基于粗糙熵的区间数离散化算法,按照决策属性离散化决策表中的条件属性,没有改变决策表的相容性。本文的决策属性中有4个区间,故最终离散化的条件属性有4个样本区间,这样利于模糊神经网络初始的隶属度函数提取。基于模糊神经网络稳定性判定初始的隶属度函数的选取,对样本训练准确性及训练时间有很大的影响[15]。由于模糊隶属度函数的形状对网络性能影响不大,本文建立的模糊神经网络模型的隶属度函数是高斯函数。第i个条件属性的第j个模糊集合的隶属度函数如式(5)所示。
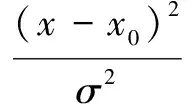
(5)
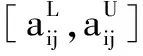
根据高斯函数的特性,当输入量x距离中心很近时,输入隶属于其他模糊量的隶属度通常小于0.5。本文取0.24,把它赋值给隶属度函数,就可以计算出初始标准差σ,这样每个条件属性有4个模糊集合。这里将其分别定义为“小”、“偏小”、“适中”、“大”。通过计算得到部分样本燃烧参数的模糊区间的隶属度函数中心值如表1所示。
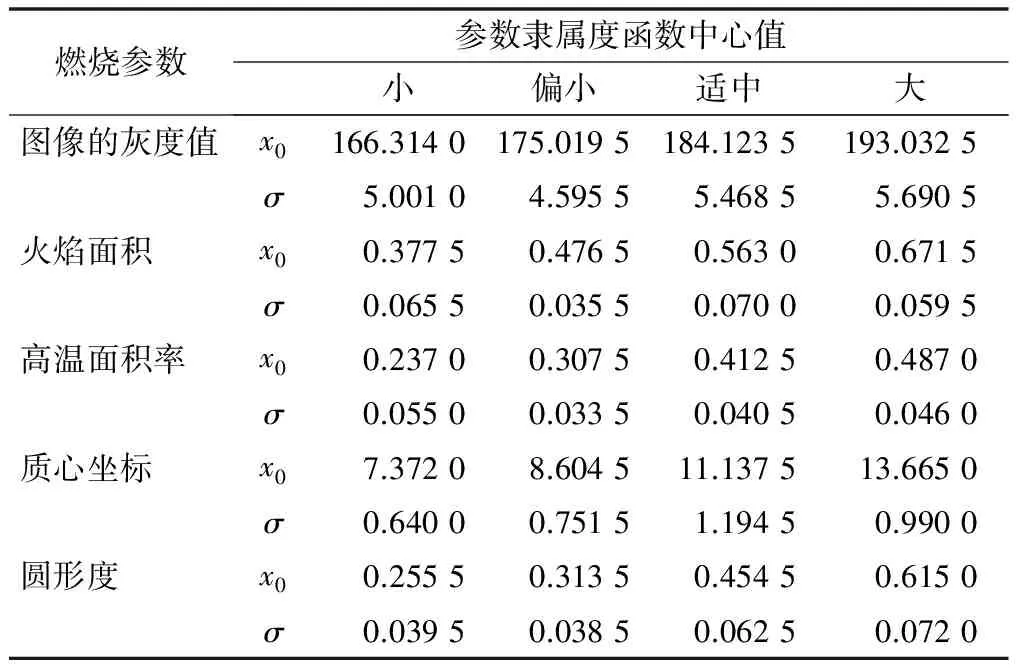
表1 隶属度函数中心值
火焰平均灰度的隶属度函数如图2所示。
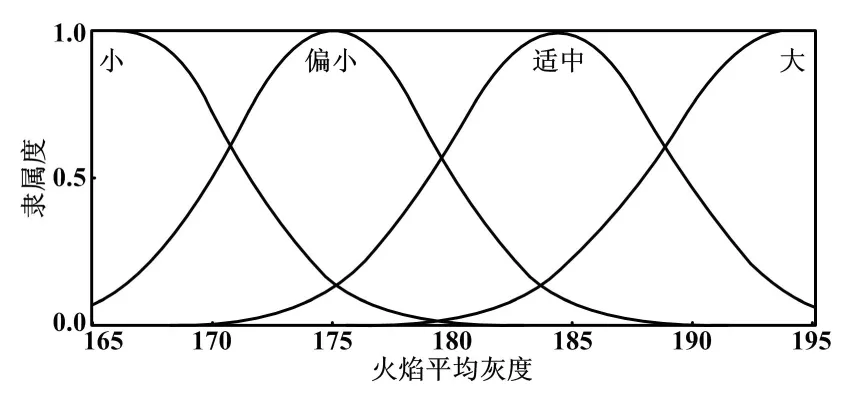
图2 火焰平均灰度的隶属度函数
火焰在不同状态下,状态变量参数是不一样的,例如火焰脉动用灰度值即可判定,其余几个参数并没有发挥很大的作用,其他燃烧在不同工况特征参数反应情况不同,故经粗糙熵离散化后的样本决策库并不是最简决策库。为了更显著地提高系统的训练效果,简化样本决策库。这里选用文献[11]中的基于粗糙集理论的规则提取方法简化和提取离散后的离散决策表。粗糙集可以处理不完整、多变量的数据,不需要关于数据的任何先验知识或额外的信息,可实现属性简约和属性值简约。经计算,最终有36条规则,则模糊控制规则可以表示为模糊推理的形式,例如选取一条已经提取的规则,如:
If(“图像灰度值”is“小”)and(“高温面积率”is“偏小”),then(“燃烧稳定性”is“一般稳定”)。
4 火焰燃烧稳定性判定仿真
4.1 T-S模糊神经网络建模与训练
本文构建的基于T-S模糊神经网络的燃烧稳定性判定模型,一共有5个输入变量、1个输出变量。输入变量分别是火焰平均灰度、火焰丰度、有效区平均灰度、高温区面积率和质心偏移。每个输入变量对应4个模糊化变量,将该模型定义为“五四模型”,其结构如图3所示。

图3 “五四模型”结构图
由于本文在之前已经确定了燃烧状态输入分量的模糊分割数,因此在训练和学习的过程中,把后件网络的连接权值、前件网络第二层节点隶属度函数的中心值以及宽度作为主要参数。本文建立的模糊神经网络模型步骤如下。
①建立初始FIS模型,增加ANFIS编辑器输入变量至5个,修改输入输出变量信息。
②编辑初始隶属度函数,根据表1所示的隶属度函数中心值及聚类中心,设定初始隶属度函数。
③根据3.2节获取的模糊推理规则,输入模糊规则域值,建立初始T-S模糊神经网络燃烧稳定性判定模型(“五四模型”)结构图。
④导入训练数据、训练模型,基于粗糙集得到训练样本2 000个和测试样本500个。
⑤训练完成后,将测试样本输入到模型中,并计算模型的准确率,用P表示,P=(模型输出经四舍五入与样本一致的离稳度)/(样本总数)×100%,表示为模型输出与样本一致的情况占总样本的比例。当模型准确率P满足要求时,该模型即可用来进行燃烧稳定性判定;否则重新训练和测试该模型,直至满足要求。
训练步数被设置为2 000步,图4为“五四模型”训练误差曲线。由图4可知,在模型训练2 000步左右时,误差接近为0。
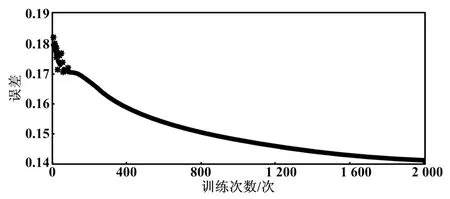
图4 “五四模型”训练误差曲线
4.2 火焰燃烧稳定性判定输出
对已经训练好的判定模型,本文选取500个测试样本参数,输入到所建立的神经网络模型中。燃烧特征参数训练前后隶属度函数对比如图5所示。
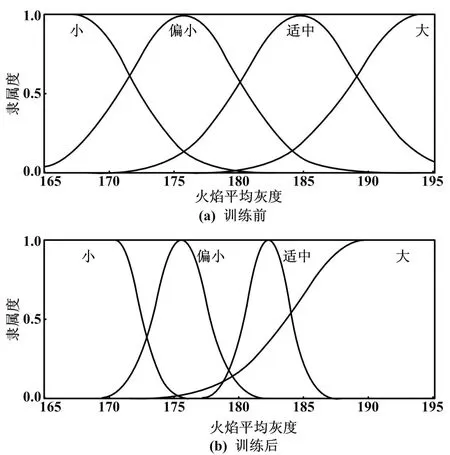
图5 隶属度函数对比图
经过计算,模型准确率为95.2%。火焰丰度、高温区面积率、质心偏移距离和有效区平均灰度的隶属度函数的变化情况同火焰平均灰度相似,故没有逐一列出。由图5可知,训练后的模糊隶属度发生了变化,相邻区间的交集减小,宽度减小,稳定性判定更为准确有效。因此利用基于T-S模糊神经网络的“五四模型”对燃烧稳定性进行判定是可行的,能适应工程要求。
5 结束语
燃烧稳定性判定是锅炉安全运营急需解决的问题,本文提出了基于“五四模型”的火焰燃烧稳定性判定模型,用于对炉腔火焰图像燃烧稳定性进行识别。模糊神经网络具有自适应性和自学习性,在燃烧稳定性判定时可通过网络学习来调整判别规则,以适应各种复杂燃烧状况。最后将获取的参数对搭建的模型进行训练和测试。通过样本测试数据表明,该判别方法是可行的,为锅炉燃烧稳定性判别建立了一个新的理论模型。
[1] 徐宝昌,张丁元,程亮.基于图像的火焰稳定性判别方法研究[J].计算机工程与应用,2012,48(9):168-171.
[2] 张清宇.火焰燃烧稳定性诊断方法研究[D].杭州:浙江大学,2004.
[3] KAMARTHI S V,PITTNER S. Accelerating neural network training using weight extrapolations[J]. Neural Networks,1999,12(9):1285-1299.
[4] SRINIVAS M,PATNAIK L M. Adaptive probabilities of crossover and mutation in genetic algorithms[J]. IEEE Transactions on Systems Man & Cybernetics,2002,24(4):656-667.
[5] 刘禾.基于火焰图像和模糊神经网络的锅炉燃烧稳定性判别[J].仪器仪表学报,2008,29(6):1280-1284.
[6] 安爱民,杨国强,张浩琛,等.基于T-S模糊决策的PMSG风电系统广义预测控制[J].自动化仪表,2016,37(9):1-5.
[7] 董喜梅,杨磊,崔浩,等.基于图像处理的火焰检测算法研究[J].后勤工程学院学报,2011,27(2):90-96.
[8] CHEN R B,FAN W T,BIAN J C,et al. Research on stability criterion of furnace flame combustion based on image processing[C]//International Conference on Control Engineering and Communication Technology,2012:568-572.
[9] CHEN R B,BIAN J C,MENG F H. Research on closed-loop control system based on image-signal processing of furnace flame[J]. Advanced Materials Research,2012,61(5):1095-1100.
[10]陈荣保,孟芳慧,肖本贤,等.基于区间数和多属性决策的燃烧稳定性研究[J].仪器仪表学报,2015,36(3):552-559.
[11]CHEN R B,MA W Y,XIAO B X,et al. Study on the parameter discretization algorithm of furnace flame image based on rough set theory[C]//2016 35th Chinese Control Conference(CCC),2016.
[12]TAKAGI T,SUGENO M. Fuzzy identification of systems and its applications to modelling and control [J]. IEEE Transaction on SMC,1985,15(1):116-118.
[13]张维杰,田建艳,王芳,等.改进型T-S模糊神经网络风电功率预测模型的研究[J].自动化仪表,2014,35(12):39-42.
[14]卜明玮,孙名松,周梦熊.基于T-S模型FNN的网络入侵检测方法研究[J].自动化技术与应用,2007,26(8):1-3.
[15]刘海,夏明波.T-S模糊神经网络及其在主动式集群中的应用[J].现代计算机(专业版),2007(4):66-68.
Flame Combustion Stability Determination Based on “5-4 Model”
CHEN Rongbao,CAO Zipei,XIAO Benxian
(School of Electrical and Automation Engineering,Hefei University of Technology,Hefei 230009,China)
Stability determination of combustion is one of the key issues to be solved in the automatic monitoring of boiler combustion state. For the purpose of automatic monitoring and quantizing the combustion stability degree,according to the digital image processing technology,the combustion parameters are extracted from flame images of furnace cavity and the database of combustion parameters is built. Based on multi-attribute determination method,the interval number sample decision library is generated. In fuzzy inference,for obtaining the membership function parameters and fuzzy rules,the simplified sample decision database is proposed based on rough set. According to the condition attributes of discretized decision database,the simplicity of attributes and their values are realized,and the reliability of sample parameters of network training is increased. Combining the logical inference of fuzzy network and the advantages of neural network,such as good learning ability,parallel computing,etc.,a T-S fuzzy neural network model is built to diagnose combustion. Appropriate number of fuzzy divisions is selected; and “5-4 Model” is defined; and the determination model of flame combustion stability is built based on “5-4 Model”; and simulation experiment is carried out. Contrasting the parameters of simulation diagrams before and after training,the results show that the model is feasible.
Combustion stability; Flame image processing; Sample decision database; Membership function; Rough set; Discretization; T-S fuzzy neural network; Number of divisions; 5-4 model
陈荣保(1960—),男,博士,副教授,主要从事DSP、图像建模、检测技术、智能仪表、过程控制的研究。 E-mail:crbwish@126.com。 曹子沛(通信作者),女,在读硕士研究生,主要从事图像建模和智能仪表的研究。E-mail:caozipei@163.com。
TH183;TP183
A
10.16086/j.cnki.issn1000-0380.201707008
修改稿收到日期:2017-01-12

