具有半正非线性项的一阶离散分数阶边值问题的正解

程伟，徐家发

(重庆师范大学数学科学学院，重庆401331)

具有半正非线性项的一阶离散分数阶边值问题的正解

程伟，徐家发

(重庆师范大学数学科学学院，重庆401331)

研究具有半正非线性项的一阶离散分数阶边值问题。借助与格林函数相关的不等式，在非线性项超线性、次线性增长的条件下，运用不动点指数获得该问题正解的存在性，推广和完善了已有的一些结果。

离散分数阶边值问题；不动点指数；正解；半正非线性项

近年来分数阶问题掀起了研究的热潮。数学家们研究发现运用分数阶模型能更精确地模拟现实问题，在分形和多孔介质中的弥散、电容理论、电解化学、半导体物理、湍流、凝聚态物理、黏弹性理论、生物数学及统计力学中有广泛应用。然而我们注意到，目前所涉及到的问题几乎都是微分方程，对于分数差分方程却鲜有问津。郑祖庥教授[1-2]指出：“对于分数微分方程来说，离散化或者问题提出时便是离散的分数差分方程是不可避免的。迄今只作为近似解计算的出发点，没有对分数差分方程的专门研究，因此，无论从理论还是应用的角度看，这都是极大的缺憾”。然而，近期已有许多学者致力于研究分数阶差分方程[2-10]，程金发在其专著[2]中系统总结了该方向的相关成果，为后续研究奠定了基础。

另一方面，运用微分方程刻画和模拟现实世界中的诸多实际问题，需要考虑大量不确定的物理变量、参数以及扰动因素等的影响。例如荷兰化学家Aris在研究化学反应时，发现一些惰性材料、 催化剂等对整个反应起到加速或抑制的作用，从而在所对应的微分方程中自然含有某个扰动项，即非线性项具有形式f(t,x)≥-M,M>0,这就是数学模型中的半正问题。该类问题来源于现实生活，所以对这些具体或抽象的变号非线性微分方程及系统模型中的数学问题的研究无疑具有现实背景和应用价值。

本文基于以上两个方面，运用不动点指数研究如下具有半正非线性项的离散分数阶边值问题正解的存在性：

(1)

其中Δν是一离散分数阶算子，0<ν<1,ν∈R,[0,T]Z=[0,T]∩Z且非线性项f满足：

(H1)f∈C([ν-1,ν+T-1]Zν-1×R+,R)且存在一正数使得

f(t,y)≥-M,∀(t,y)∈

[ν-1,ν+T-1]Zν-1×R+

其中Zν-1={ν-1,ν,…}。

1 基础知识及主要结论

首先给出离散分数阶计算的相关定义及基本知识，详细内容参见文献[2-3]。

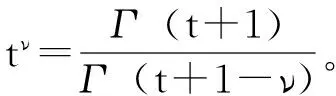
定义2 当ν>0时，函数f的ν阶和分定义为

并且当ν>0时，定义f的ν阶分数差分为

Δνf(t)=ΔNΔν-Nf(t)

其中t∈Na+ν,N是自然数且满足0≤N-1<ν≤N。

以下研究问题(1)的格林函数及其性质。定义G:[ν-1,ν+T-1]Zν-1×[0,T]Z→(0,+∞)如下：

G(t,s)=

(2)

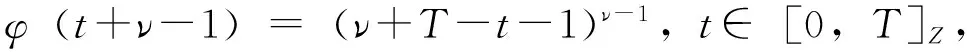
φ(t+ν-1)·φ(s+ν-1)≤

φ(t+ν-1)·φ(s+ν-1)

(4)

为了方便，令

令E是从[ν-1,ν+T-1]Zν-1到实数集的全体映射构成的集合，并在其上赋予通常的最大模范数则(E,‖·‖)是一Banach空间。考虑定义其上的锥K⊂E为

以下证明存在足够大的M1>0，当y∈K,‖y‖≥M1时，有

(5)

其中w是以下辅助问题的解

(6)

根据文[4]的讨论知，问题(6)的解可以表示为

(7)

从而可得

因此，若y∈K, 取

则对任意的[ν-1,ν+T-1]Zν-1, 当‖y‖≥M1时，有

为了获得问题(1)正解的存在性，需考虑如下

(8)

其中w由式(7)定义。容易证明：

(i) 若y和w分别是问题(8)和问题(6)的解，并且对任意的t∈[ν-1,ν+T-1]Zν-1，有(y-w)(t)≥0，则y(t)-w(t)是问题(1)的正解；

(ii) 若y是问题(1)的正解，则y(t)+w(t)是问题(8)的正解。因此，只需找寻问题(8)的且超过w的解。

定义算子A:E→E如下

max{y(s+ν-1)-w(s+ν-1),0})+M]

则根据Arzelà-Ascoli定理可得A是E上的一全连续算子，并且问题(8)解的存在性等价于算子A不动点的存在性。注意到式(3)，容易证明A(K)⊂K。

u≠Au+λu0,∀u∈∂Ω∩P,λ≥0

则i(A,Ω∩P,P)=0，其中i为锥P上的不动点指数。

u≠λAu,∀u∈∂Ω∩P,λ∈[0,1]

则i(A,Ω∩P,P)=1。

最后，列出本文使用的假设条件和主要结论。

(H3) 对任意的(t,y)∈[ν-1,ν+T-1]Zν-1×[0,M1],有

(H5) 对任意的(t,y)∈[ν-1,ν+T-1]Zν-1×[0,M1],有

其中,f*(t,y)=f(t+ν-1,max{y(t+ν-1)-w(t+ν-1),0})+M。

定理1 若条件(H1)-(H3)满足，则问题(1)至少有一个正解。

定理2 若条件(H1), (H4), (H5)满足，则问题(1)至少有一个正解。

2 主要结论的证明

令

Bρ={y∈E:‖y‖<ρ,ρ>0}

定理1的证明 根据第一部分的论述，仅需找寻范数超过M1的算子A的不动点。

第1步： 证明存在足够大的R>M1使得

y≠Ay+λy0,∀y∈∂BR∩K,λ≥0

(9)

其中y0∈K是一给定元素。事实上，若式(9)不成立，则存在y∈∂BR∩K,λ0≥0使得

y=Ay+λ0y0

由(H2)可知存在ε1>0,c1>0使得

∀(t,y)∈[ν-1,ν+T-1]Zν-1×R+

结合上述两式可得

在上式两端乘以φ*(t)，并在ν-1到ν+T-1上求和，注意到式(4)，有

从而由上式解得

另一方面，注意到y∈K，有

‖y‖φ(t+ν-1)≤

从而

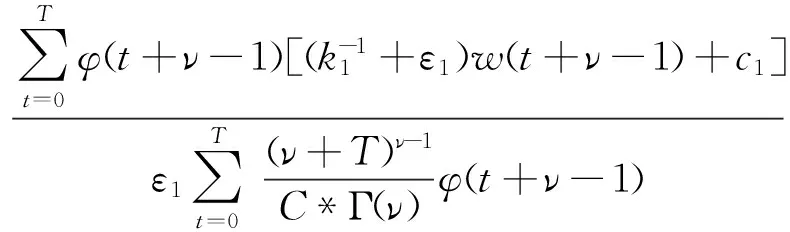
所以当R>max{M1,M2}时，式(9)成立, 从而根据引理1知

i(A,BR∩K,K)=0

(10)

第2步：证明

y≠λAy,∀y∈∂BM1∩K,λ∈[0,1]

(11)

若上式不成立，则存在y∈∂BM1∩K,λ0∈[0,1]使得y=λ0Ay，从而‖y‖≤‖Ay‖。 然而根据条件(H3)，有

这表明‖Ay‖<‖y‖=M1,y∈∂BM1∩K矛盾。从而式(11)成立。再由引理2知

i(A,BM1∩K,K)=1

(12)

结合式(10)和式(12)，有

定理2的证明

第1步： 证明存在足够大的R>M1，使得

y≠λAy,∀y∈∂BR∩K,λ∈[0,1]

(13)

否则的话，则存在y∈∂BR∩K,λ0∈[0,1]使得

y=λ0Ay

根据条件(H4)，存在ε2>0,c2>0使得

∀(t,y)∈[ν-1,ν+T-1]Zν-1×R+

综上两式可得

[y(s+ν-1)-w(s+ν-1)]+c2]≤

在上式两端乘以φ*(t)，并在ν-1到ν+T-1上求和，并运用式(4)，有

从而解得

另一方面，注意到y∈K,有

‖y‖φ(t+ν-1)≤

从而

所以当R>max{M1,M3}时，式(13)成立, 从而根据引理2知

i(A,BR∩K,K)=1

(14)

第2步：证明

y≠Ay+λy0,∀y∈∂BM1∩K,λ≥0

(15)

其中y0∈K是一给定元素。若上式不成立，则存在y∈∂BM1∩K,λ0≥0使得y=Ay+λ0y0，从而‖y‖=‖Ay+λ0y0‖≥‖Ay‖ 然而由条件(H6)知

这表明‖Ay‖>‖y‖=M1,y∈∂BM1∩K矛盾。从而式(15)成立。再由引理1知

i(A,BM1∩K,K)=0

(16)

结合式(14)和式(16),有

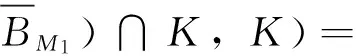
i(A,BR∩K,K)-i(A,BM1∩K,K)=

1-0=1≠0

[1] 郑祖庥. 分数微分方程的发展和应用[J]. 徐州师范大学学报(自然科学版), 2008, 26(2): 1-10.ZHENGZX.Onthedevelopmentsandapplicationsoffractionaldifferentialequations[J].JournalofXuzhouNormalUniversity(NaturalScienceEdition), 2008,26(2):1-10.

[2] 程金发. 分数阶差分方程理论[M]. 厦门: 厦门大学出版社, 2011.

[3]ATICIFM,ELOEPW.Atransformmethodindiscretefractionalcalculus[J].InternationalJournalofDifferenceEquations, 2007, 2(2): 165-176．

[4]GOODRICHCS.Onafirst-ordersemipositonediscretefractionalboundaryvalueproblem[J].ArchivderMathematik, 2012, 99(6): 509-518.

[5]GOODRICHCS.Ondiscretesequentialfractionalboundaryvalueproblems[J].JMathAnalAppl, 2012, 385(1): 111-124.

[6]FERREIRARAC.Existenceanduniquenessofsolutiontosomediscretefractionalboundaryvalueproblemsoforderlessthanone[J].JournalofDifferenceEquationsandApplications, 2013, 19(5): 1-7.

[7]LVZ,GONGY,CHENY.Multiplicityanduniquenessforaclassofdiscretefractionalboundaryvalueproblems[J].ApplicationsofMathematics, 2014, 59(6): 673-695.

[8] 王金华，向红军. 一类分数阶差分方程边值问题多重正解的存在性[J]. 高校应用数学学报，2016, 31(2): 167-175.WANGJH,XIANGHJ.Existenceofmultiplepositivesolutionsforaboundaryvalueproblemoffractionaldifferenceequation[J].AppliedMathematicsAJournalofChineseUniversities, 2016, 31(2) : 167-175.

[9] 王金华，向红军，赵育林. 一类非线性分数阶差分方程边值问题解的存在性及Ulam稳定性[J]. 中山大学学报(自然科学版), 2016, 55(2): 1-6.WANGJH,XIANGHJ,ZHAOYL.ExistenceandUlamstabilityofsolutionsforaboundaryvalueproblemofnonlinearfractionaldifferenceequation[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2016, 55(2): 1-6.

[10] 袁利国. 分数阶时滞广义Logistic方程解的研究[J]. 中山大学学报(自然科学版), 2014, 53(2): 44-48.YUANLG.Researchonsolutionsoffractional-ordergeneralizedlogisticequationwithdelay[J].ActaScientiarumNaturaliumUniversitatisSunyatseni, 2014, 53(2): 44-48.

[11] 杨志林. 非线性二阶常微分方程Robin问题的正解[J]. 青岛理工大学学报, 2013, 34(1): 5-15.YANGZL.PositivesolutionsoftheRobinproblemfornonlinearsecond-orderordinarydifferentialequations[J].JournalofQingdaoTechnologicalUniversity, 2013, 34(1): 5-15.

Positivesolutionsforafirst-orderdiscretefractionalboundaryvalueproblemwithsemipositonenonlinearity

CHENGWei,XUJiafa

(SchoolofMathematicalSciences,ChongqingNormalUniversity,Chongqing401331,China)

A first-order discrete fractional boundary value problem with semipositone nonlinearity is studied. By virtue of some inequalities associated with Green function, and using the fixed point index, the existence of positive solutions is obtained for the problem, with the nonlinearity grows both superlinearly and sublinearly. The results extend known results.

discrete fractional boundary value problem；fixed point index；positive solution；semipositone nonlinearity

10.13471/j.cnki.acta.snus.2017.04.005

2016-12-16 基金项目：国家自然科学基金(11601048)；重庆市基础与前沿研究计划资助项目(cstc2016jcyjA0181)；重庆市教委科学技术研究项目(KJ1703050)；重庆师范大学项目(15XLB011,16XYY24)

程伟(1985年生)，男；研究方向：微分方程、拓扑动力系统；E-mail: 1375415619@qq.com

徐家发(1986年生)，男；研究方向：微分方程、非线性泛函分析；E-mail：xujiafa292@sina.com

O

A

0529-6579(2017)04-0023-05