一种高精度机扫被动超视距雷达测向方法

岳帅英,付 林,顾毅君

(中国船舶重工集团公司第七二四研究所,南京211153)

一种高精度机扫被动超视距雷达测向方法

岳帅英,付 林,顾毅君

(中国船舶重工集团公司第七二四研究所,南京211153)

将最小方差估计法应用到机扫被动超视距雷达测向中,在特定应用条件下提高了测向精度。分析了被动截获信号的脉冲能量-空间分布特征,仿真研究了该方法的测向精度对天线调制、截获次数的依赖关系。仿真结果表明,针对低频段、低速运动的海上辐射源目标,采用最小方差估计法测向可获得比现有方法更高的测向精度。实验验证了其工程适用性。

被动超视距雷达;测向精度;最小方差估计;天线调制

0 引 言

高精度测向方法一直是雷达信号处理和数据处理领域的研究热点。针对不同体制雷达,人们发展出了各类测向方法,如单脉冲比幅测向、干涉仪测向、角度谱估计等。[1-6]与具有多功能和高测角精度的相控阵雷达相比,传统的机扫雷达因其成本优势仍然有其存在的价值。适用于宽频段、大辐射源运动速度范围的高精度机扫被动测向方法仍有待完善。本文探索一种针对舰载辐射源目标的高精度被动测向方法。

机扫雷达对截获的辐射源脉冲信号进行参数测量形成脉冲描述字(PDW)数据,再对其进行信号分选和目标融合处理得到高精度的辐射源方位信息。在保证雷达威力的条件下,被动雷达天线能够截获辐射源信号的波束宽度远远超过-3 dB波宽,甚至副瓣也可以接收到信号。如此宽的截获角度范围都能收到信号,测角误差将会很大。传统的最大信号法[2-4]、起止中间时刻法,测向精度较低而且存在较大的起伏,非常不利于工程应用。文献[7]提出的解方程法在截获次数不够多时能够得到比传统方法更高的测向精度,但要求被动雷达天线方向图形状与近似曲线匹配较好。本文从单程雷达方程出发分析了截获信号能量-角度的数学关系;从参数估计的角度,利用被动探测天线方向图信息和截获信号功率、角度观测值,估计目标真实方位,使截获信号功率随机误差均方根最小。仿真分析了该方法的测向精度与天线调制、单周期截获辐射源次数的关系,对比了该方法与其他现有方法的测向精度。结果表明,在探测低频段、低速运动辐射源时,最小方差估计测向法能够获得比其他方法更高的测向精度,并且测向精度在天线调制改变时起伏不大。

1 测向方法设计

1.1 截获信号的能量-角度分布规律

如图1所示,设被动雷达天线作扇扫,扫描中心为θc,范围为θR,角速度ωr;辐射源信号频率在被动接收频段范围内,辐射源真实方位为θ0,天线作环扫,扫描角速度为ωe;能够截获辐射源信号的被动天线波束宽度为△θb。θ(t)为t时刻被动雷达天线指向。

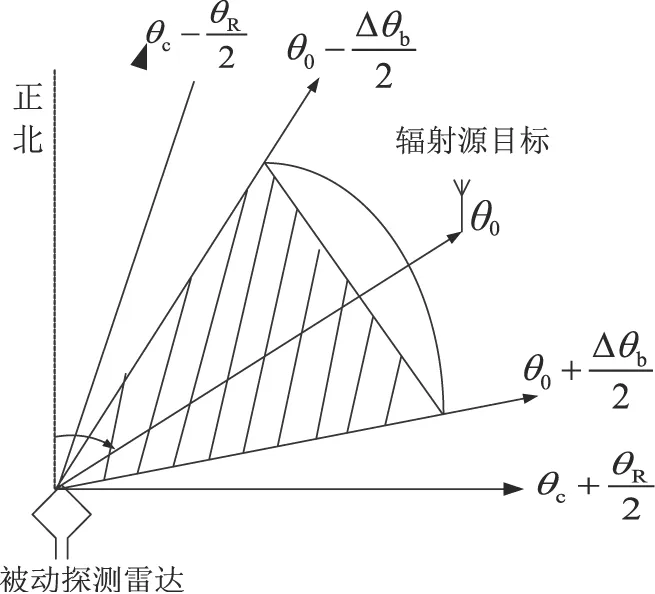
图1 被动雷达天线扫描示意图

建立如下单程雷达方程:

Ga≥Gate(dBW)

(1)

由于主要考察天线调制对截获的影响,忽略超视距条件下的对流层散射损耗衰落效应[5],大气传输损耗按照张氏模型取中值。辐射源(辐射频率f、发射功率Pt、天线增益Gt、传输距离R、传输损耗L)和被动雷达接收系统(天线增益Gr、接收机增益Ga、接收机门限Gate)一定时,△θb基本确定。

由式(1)知,天线方向图曲线决定了截获信号的能量-角度关系P(θ(t),θ0)。实际上,单次截获的脉冲信号的能量-角度分布符合目标天线方向图包络。当降低探测天线的转速使得单个被动扫描周期截获辐射源信号多次(多个辐射源天线周期)时,各次截获的脉冲信号的峰值能量-角度分布符合被动雷达天线方向图包络。

截获信号的角度-时间关系可以用窗函数理论[2-3]来描述。当雷达功率和辐射源位置确定时天线的调制形成了特定的窗函数关系,此时截获信号的角度-时间分布以被动天线往返扫描周期与辐射源天线周期的最小公倍数为周期重复。[7]这将导致单周期测角误差周期性分布。提高测向精度的途径之一是寻求合理的单周期测角方法来提高单周期测角精度并减小受天线调制的影响。

1.2 最小方差估计测向法

利用雷达截获信号的能量-角度分布规律可以测量辐射源方位。取单次截获脉冲中能量为峰值的PDW数据θ(t),式(1)可简化为

(2)

式中,f(θ)为被动雷达天线方向图包络函数;C包含辐射源发射功率、天线最大增益、传输损耗等,与角度无关。

对海超视距被动探测应用中,单个被动扫描周期内辐射源真实方位变化非常小,辐射源真实方位可视为未知常量。接收机噪声可以用N(0,σ2)的正态分布描述。因此,利用PDW数据可以通过最小方差估计求解辐射源真实方位。假设单周期截获目标M次,每次截获的峰值PDW的功率、方位观测值为yi、θi,则

(3)

其中,f为式(1)中的第1项,C为式(1)中的常数项,M值与被动天线波束宽度、被动天线扫描速率、辐射源天线扫描周期有关。实际工程中M值不能做到很大。令观测值yi与理论值的均方误差为

(4)

2 算法验证与分析

由于机扫雷达被动测向误差分布与天线调制紧密相关,许多测向方法,如起始终止法、质心法等[7]的精度,都会随天线调制改变而起伏。本节仿真分析了最小方差测向法的测向精度受天线调制的影响。

在其他参数不变、辐射源功率增大或者被动扫描角速度降低的条件下,单个被动扫描周期截获辐射源的次数将增加,原则上将改善测向精度。仿真分析了截获次数对最小方差估计法测向精度的影响。

假设被动雷达接收天线副瓣抑制效果良好,天线指向误差已校正,且考虑只有一个辐射源。在相同条件下,将本方法与最大信号法、质心法、解方程法进行对比。

2.1 仿真验证与分析

(1) 测向精度随天线调制的变化

通过改变双方天线起始指向、被动天线扫描中心或者被动雷达天线扇扫边界时间延迟等参数中的一项,可改变天线调制,最终改变截获辐射源脉冲信号的角度。

假设辐射源平台不运动,位于被动雷达威力和天线扫描范围之内,辐射源天线环扫周期Te=4s,被动雷达天线扇扫范围θR=22.5°,扫描周期TTr=45s。在某辐射源功率和探测距离下,被动截获波束宽度△θb≈6.5°,截获窗宽τTr≈13s,单个被动扫描周期可截获目标3～4次。以辐射源天线起始指向θin-e=63°为例,考察特定天线调制下的截获脉冲的能量-角度分布和各测向方法的误差,见图2。使辐射源天线起始指向θin-e在0°～360°范围内改变,其他参数不变,考察各θin-e下的测向结果(RDW方位)相对辐射源方位真值的均方根误差。针对每个θin-e仿真30～40个被动扫描周期,见图3。

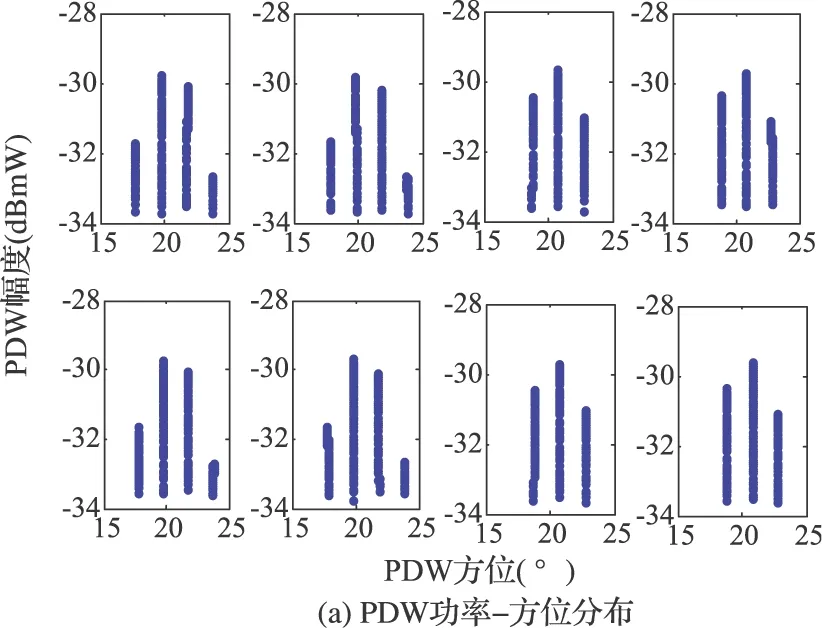
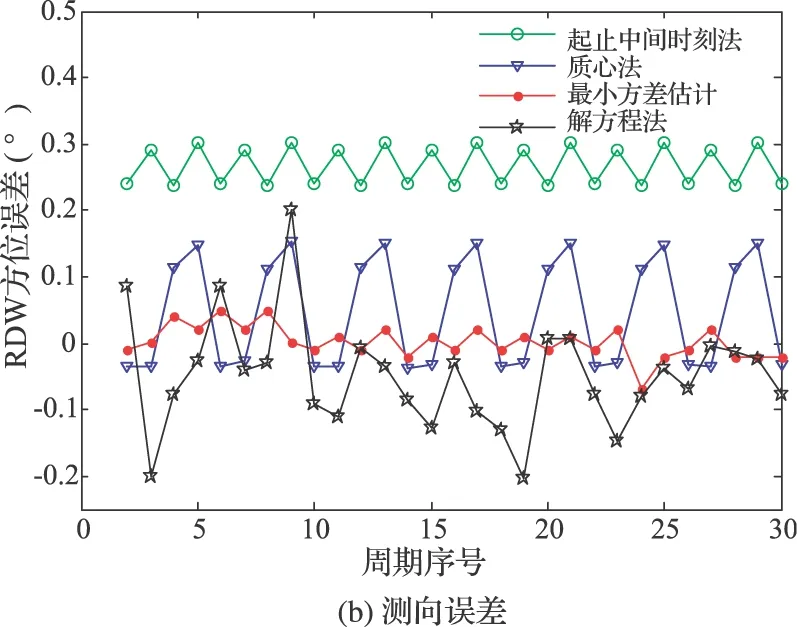
图2 PDW功率-方位分布与测向误差(辐射源天线起始指向63°)

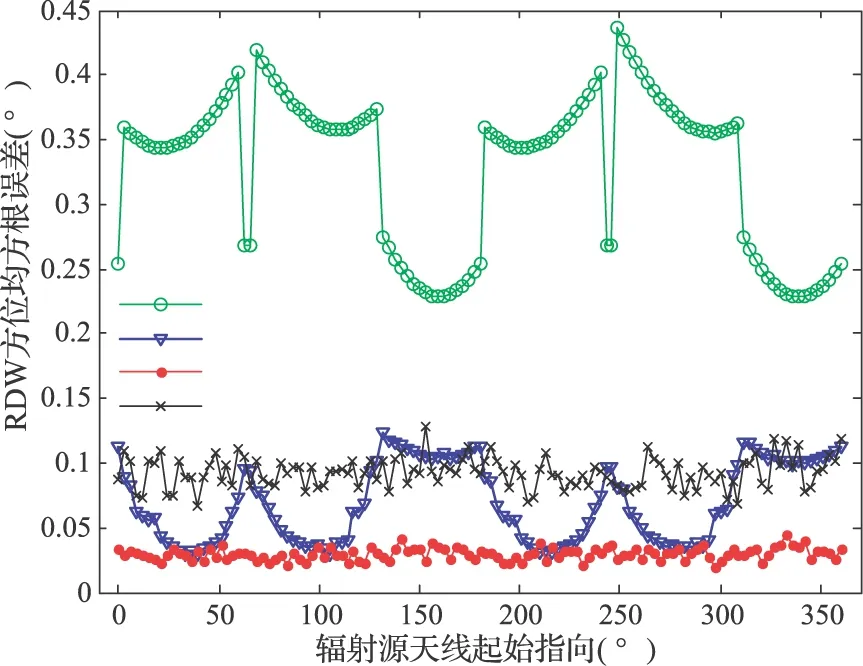
图3 测向精度随辐射源天线起始指向的变化

图2(a)为θin-e=63°时第2～9周期的PDW分布,图2(b)为最小方差估计法和其他方法的单周期测向误差。由于首、尾两个扫描周期被动天线不一定严格开始和结束于扫描边界,为避免数据不全导致测向精度降低,舍弃首、尾周期数据。图2(a)显示PDW能量-角度分布在相邻周期间不同。这是因为扫描中心与辐射源方位不重合,往返周期截获位置不同,并且PDW分布近似以4个被动扫描周期(照射窗和截获窗的最小公倍数)为周期重复。之所以为“近似”周期性重复,是因为仿真模拟了被动雷达天线扫描边界延时、真实雷达接收机内部噪声和雷达信号处理分机参数(到达时间、幅度等)测量误差。图2(b)中的RDW方位误差为单周期测向结果相对辐射源真实方位的误差。当前调制状态下,质心法的误差在周期间起伏最大,最小方差估计法误差起伏最小。图2(b)测向误差的周期性证实了图2(a)中PDW的“近似”周期性重复特性。

图3显示:(1)随着辐射源天线起始指向改变,信号截获角度周期性改变,测向精度亦周期性变化;(2)测向精度变化的方差依次是起止中间时刻法最大,质心法次之,最小方差估计测向法和解方程法则非常小。最小方差估计法利用观测数据通过后验估计真实辐射源方位,其受天线调制的影响应当与采样点数多少有关,采样点数越多,精度越高。解方程法由单周期截获的两次峰值PDW的功率和方位代入天线方向图近似曲线方程得到,原则上受天线调制影响非常小。

实际应用中,辐射源天线参数未知,相对不同批次的被动探测行为它是随机的。测向精度随天线调制改变显然不能满足高性能装备的指标要求。最小方差估计测向精度相对维持稳定,其军事应用价值显而易见。同样利用了被动天线方向图先验信息的解方程法,虽然测向精度随天线调制起伏也不明显变化,但在被动雷达天线方向图形状与近似曲线匹配度下降时误差将增大。此时应用最小方差估计法在一定程度上能避免该问题。

(2) 测向精度随截获次数的变化

设置被动扫描速率不变,增大辐射源功率使得单周期截获辐射源次数增加。针对每一种截获次数仿真考察测向精度随天线调制的变化,统计其均值和方差,结果见图4。其中单周期截获次数是指可能截获的最小次数Nmin。假设辐射源雷达天线环扫周期Te=4s,截获时间窗宽τTr=7.5s,其可能截获的最小次数Nmin=1 。

(4)

(a)

(b)

由于解方程法要求单周期至少截获2次,所以图4中截获次数为1时解方程法没有测向精度输出。图4显示,质心法和最小方差估计法的平均测向精度随着截获次数增多而提高,尤其质心法变化趋势最明显,解方程法则基本保持不变,起止中间时刻法测向精度与截获次数的影响关系不明显。最小方差估计法测向精度整体高于其他测向方法,截获达到4次及以上后,测向精度与质心法基本接近,略优于解方程法,并都明显优于起止中间时刻法。在工程应用中,雷达发射功率与威力范围是设计好的,降低被动雷达天线扫描速率可以获得更多截获次数,但过低的扫描速率将导致数据率下降,周期间积累效果变差,甚至无法积累。此外,低频段雷达波束宽度相对于高频段更宽,其他条件相同时能获得更多截获次数。

2.2 实验验证

对低频段配合辐射源进行了视距内机械扫描被动探测真实实验和测向算法验证。辐射源平台静止。在视距范围内的电磁传输可以不考虑对流层散射损耗。单个被动扫描周期截获辐射源信号3～4次。对采集数据进行频率分选、副瓣抑制、天线方向图系统误差校正、单周期测向,对比几种方法的单周期测向精度(测向结果的均方根误差),结果见图5。

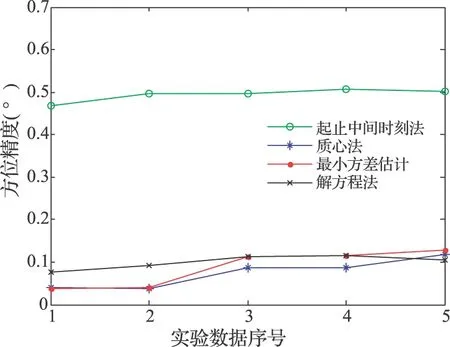
图5 对实测数据进行测向的精度

从上述实验结果可以发现:(1)该批实验数据测向精度非常高;(2)该频段下,最小方差估计法、质心法、解方程法测向精度相当,但都明显高于起止中间时刻法;(3)基本与仿真结果一致。分析其原因:(1)该批实验信号很强,单个被动扫描周期截获次数达到3～4次,用于测向已经足够多,并且电磁环境相对干净,多径效应也不明显;(2)实验中对该频段下的被动天线方向图主瓣进行曲线拟合,发现其与2次曲线匹配度高,所以解方程法的精度非常高。

3 结束语

本文以机扫被动超视距雷达截获信号分布特征为基础,提出了一种最小方差估计测向法,仿真验证了其测向精度受天线调制、被动雷达单个天线扫描周期截获次数的影响情况。结果表明:针对海上中低速运动目标进行被动测向,最小方差估计法的测向精度随着天线调制变化起伏较小,随着截获次数增大而提高;在截获次数较多的情况下该方法能获得比目前已有测向方法更高的单周期测向精度。因此,最小方差估计法比较适合针对低频段、中低速运动辐射源目标的被动探测。相应条件下的实验验证结果证实该方法的工程应用效果较好。

[1] 丁鹭飞,耿富录,陈建春.雷达原理 [M].4版.北京:电子工业出版社,2009:295-382.

[2] Richad G Wiley.电子情报(ELINT)——雷达信号截获与分析[M].吕跃广,等译.北京:电子工业出版社,2008:76.

[3] 唐永年.雷达对抗工程[M].北京:北京航空航天大学出版社,2012:212-266.

[4] David L Adamy.电子战进阶[M].朱松,王燕,姜道安,等译.北京:电子工业出版社,2009:155-193.

[5] 张明高.对流层散射传播[M].北京:电子工业出版社,2004.

[6] 王永良,陈辉,彭应宁,万群.角度谱估计理论与算法[M].北京:清华大学出版社,2004.

[7] 王西峰,岳帅英,顾毅君.机扫体制雷达超视距被动测向新方法研究[J].雷达与对抗,2015,35(4):11-14.

A high-precision direction-finding method for mechanically scanned passive OTH radar

YUE Shuai-ying, FU Lin, GU Yi-jun

(No.724 Research Institute of CSIC, Nanjing 211153)

The minimum variance estimation is applied in the direction finding of the mechanically scanned passive OTH radar to improve the direction-finding precision on the specific application conditions. The characteristics of the pulse energy-spatial distribution of the passive intercept signals are analyzed, and the impacts of the antenna modulation and the interception times on the direction-finding precision are discussed via the simulation. The simulation results indicate that the new method is superior to the conventional methods in direction-finding precision for slow moving and low frequency surface targets. Finally, the test results verify that the method is feasible in practical engineering application.

passive OTH radar; direction-finding precision; minimum variance estimation; antenna modulation

2016-10-08;

2016-11-23

岳帅英(1982-),女,高级工程师,博士,研究方向:雷达数据处理;付林(1975-),男,研究员,博士,研究方向:光学、雷达目标识别技术;顾毅君(1985-),女,工程师,硕士,研究方向:雷达系统工程。

TN953.3

A

1009-0401(2017)02-0001-04