构造对偶式 妙解六类题
蔡勇全
(四川省资阳市外国语实验学校,四川 资阳 641300)
构造对偶式 妙解六类题
蔡勇全
(四川省资阳市外国语实验学校,四川 资阳 641300)
对偶式是指形式相似并具有一定对称关系的两个数学式子.在数学解题过程中,如果能挖掘出题目中潜在的对称性,合理构造出相应的对偶式,再结合适当的加、减、乘等运算,往往能使问题获得巧妙的解决.
结构特征;构造;对偶式
有些数学问题,按常规思路寻求解答,常常由于繁琐的运算而极易出错,甚至思维一时受阻.这时若调整解题思路,根据题设条件或所求结论中某些式子的结构特征,联想并构造出能与之形成和与差、积与商、正与负、互为有理化因式、互为共轭因式、正弦与余弦、正切与余切、奇函数与偶函数等匹配类型的对偶式,然后将这两个对偶式通过合理的变换与运算,简捷高效地完成问题的解决,使陷入僵局的解答过程“拨云见日”.这样做,不仅可以极大地减少运算量,优化解题过程,起到化繁为简、化难为易的效果,而且可以较好地体现数学的对称美、奇异美、和谐美与统一美.本文结合实例介绍对偶式在解答几类数学问题时的妙用,旨在探索题型规律,揭示解题方法,供大家参考.
一、三角求值
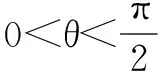
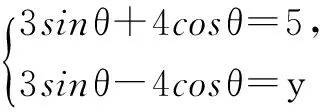
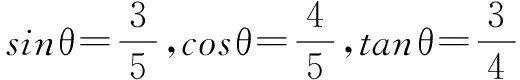
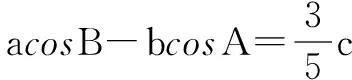
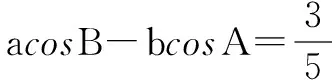
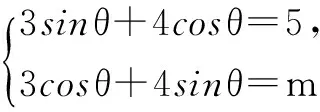
二、证明不等式或恒等式
1.证明不等式
例2 求证:2sin4x+3sin2xcos2x+5cos4x≤5.
证明 令A=2sin4x+3sin2xcos2x+5cos4x,B=2cos4x+3cos2xsin2x+5sin4x,则A+B=7(sin4x+cos4x)+6sin2xcos2x=7(sin2x+cos2x)2-8sin2x·cos2x=7-2sin22x=5+2cos22x①.
A-B=3(cos4x-sin4x)=3(cos2x-sin2x)=3cos2x②.
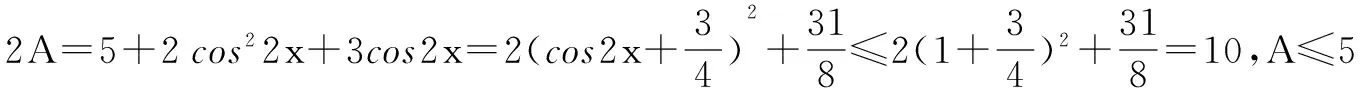
变式1 已知a,b,c,d∈R,a2+b2+c2+d2≤1,求证:(a+b)4+(a+c)4+(a+d)2+(b+c)4+(b+d)4+(c+d)4≤6.
证明 令A=(a+b)4+(a+c)4+(a+d)2+(b+c)4+(b+d)4+(c+d)4,再令B=(a-b)4+(a-c)4+(a-d)2+(b-c)4+(b-d)4+(c-d)4,A+B=6(a4+b4+c4+d4+2a2b2+2a2c2+2a2d2+2b2c2+2b2d2+2c2d2)=6(a2+b2+c2+d2)2≤6.
又B≥0,所以A≤6,即原不等式得证.
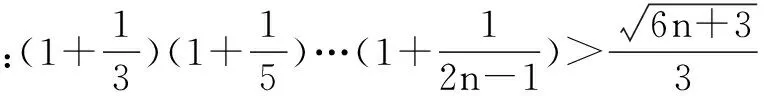
2.证明恒等式
例3 求证:sin3α·sin3α+cos3α·cos3α=cos32α.
证明 令m=sin3α·sinα·sin2α+cos3α·cosα·cos2α,且n=cos3α·cosα·sin2α+sin3α·sinα·cos2α,则m+n=cos2α,m-n=cos4α·cos2α,
所以2m=cos2α(1+cos4α)=2cos32α,m=cos32α,即原结论得证.
变式1 求证:cos2α+cos2β-2cosαcosβcos(α+β)=sin2(α+β).
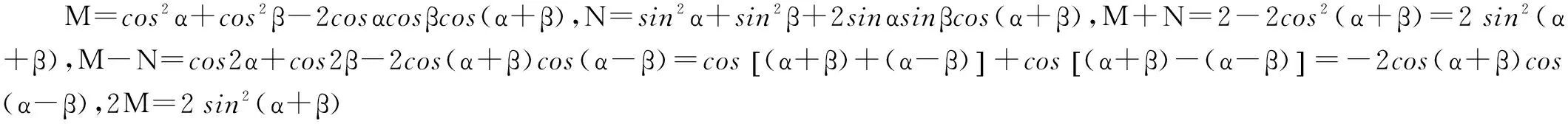
评注 从例3及其变式1可以看到,构造对偶式证明恒等式时,对于同一个式子,可以局部对偶创设其对偶式,其余部分不变.
三、求最值或取值范围
1.求最值
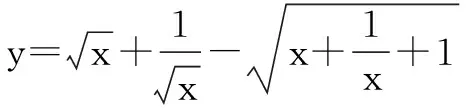
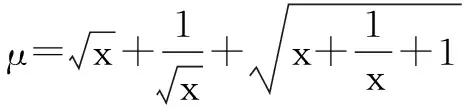
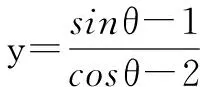
二、求取值范围
例5 已知实数x,y满足x2-3xy+y2=2,求x2+y2的取值范围.
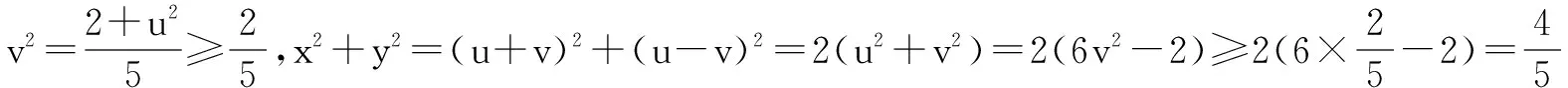
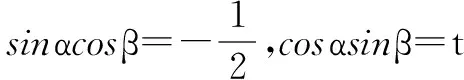
评注 对于例5的变式,题目中的两个条件式本是一组对偶式,而在解答过程中,通过逆用公式又得到了sin(α+β)与sin(α-β),从和与差的角度看,它们仍是一组对偶式,这正是解答本题的关键所在.
四、求和问题
1.函数中的求和问题
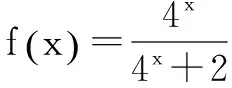
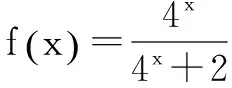
评注 从例6可以看到,构造对偶式解决函数中的求和问题时,可多次设出必要的对偶式,既体现个别(局部)性,又体现整体性.
2.二项展开式中的求和问题
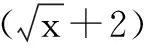
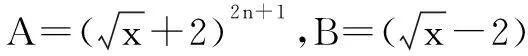
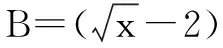
3.数列中的求和问题
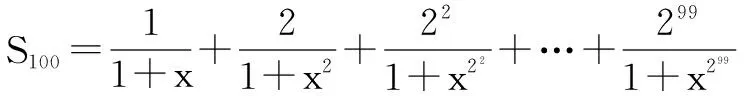
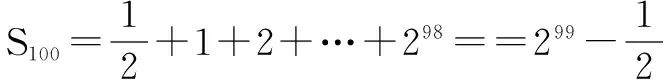
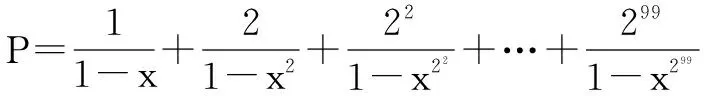
五、解方程
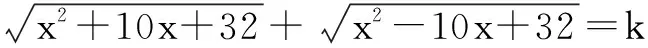
评注 从例9可以看到,对于无理方程的求解,是从和与差的视角来构造对偶式的;对于复数方程的求解,是从寻找共轭复数代数式的视角来构造对偶式的;对于三角方程的求解,是从正弦(切)对余弦(切)的角度来构造对偶式的.
六、求函数解析式
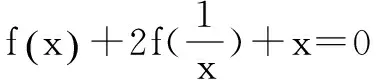
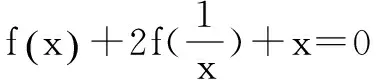
变式1 已知定义域为R的函数y=f(x)满足3f(1-x)-f(1+x)=2x+4,求函数y=f(x)的解析式.
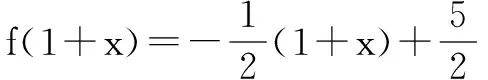
评注 若把上述变式中条件式左边改为“3f(-x)±f(x)”或“3f(a-x)±f(a+x)”,则构造对偶式的替换策略依然不会发生改变.对于变式4,其对偶构造思想体现在利用f(x)与g(x)的奇、偶性,构造出“f(x)+g(x)”与“f(x)-g(x)”这一组对偶式.
[1]蔡勇全.构造"辅助元"解题的十种策略[J].数理化解题研究,2016(5).
[2]蔡勇全.简化数学运算的若干策略[J].数学教学研究,2015(1).
[3]蔡勇全.从结构联想模型巧证不等式的着眼点[J].中学数学研究,2012(1).
[责任编辑:杨惠民]
2017-05-01
蔡勇全(1980.8-),男,四川省资阳市人,硕士,中学数学一级教师,从事数学教学.
G632
B
1008-0333(2017)16-0032-03

