空间动点轨迹问题的判断与确定

吕 涛

(广东省佛山市顺德区容山中学，广东 佛山 528303)



空间动点轨迹问题的判断与确定

吕 涛

(广东省佛山市顺德区容山中学，广东 佛山 528303)

立体几何是高考命题的重要部分，在近年的高考试题中，与立体几何交汇的一类轨迹问题不断涌现，是考生比较惧怕的一类难度较大的试题.本文力求把这些分散的问题集中起来，揭示了空间动点轨迹问题的本质，对这一类问题的解法给出了一个系统的归纳.

空间动点；轨迹问题；解题策略

《中学数学新课程标准》对学生的空间想象能力考查提出了更高要求：“能够想象几何图形的运动和变化情况”．正是这一高要求导致了近几年的高考试题或模拟试题中设置了许多与立体几何交汇的一类轨迹问题．笔者从全国高考试题和有关省市高考模拟试题中收集并归纳了这类题目，试图从解题策略上揭示题型规律，探索解题方法.

一、通过线面位置关系确定动点轨迹

例1 (2016年黄冈调考题) 平面α的斜线AB交α于点B，过定点A的动直线l与AB垂直，且交α于点C，则动点C的轨迹是( ).

A．一条直线 B．一个圆

C．一个椭圆 D．双曲线的一支

解 过点A作直线AB的垂面β有且只有一个，该平面β与平面α必相交(否则AB⊥β，α∥β⟹AB⊥α,与AB为α的斜线矛盾)于一条直线m，则直线m即为点C的轨迹，故选A．

例2 (2015北京模拟题)l1、l2是两条异面直线，在l1、l2之间有一平面α，与l1、l2都平行，且与l1、l2距离相等，求证：平面α上与l1、l2距离相等的点的轨迹是两条相交直线．

分析 先将空间几何的有关元素“集中”到平面α内，再利用平面几何知识即可顺利求解．

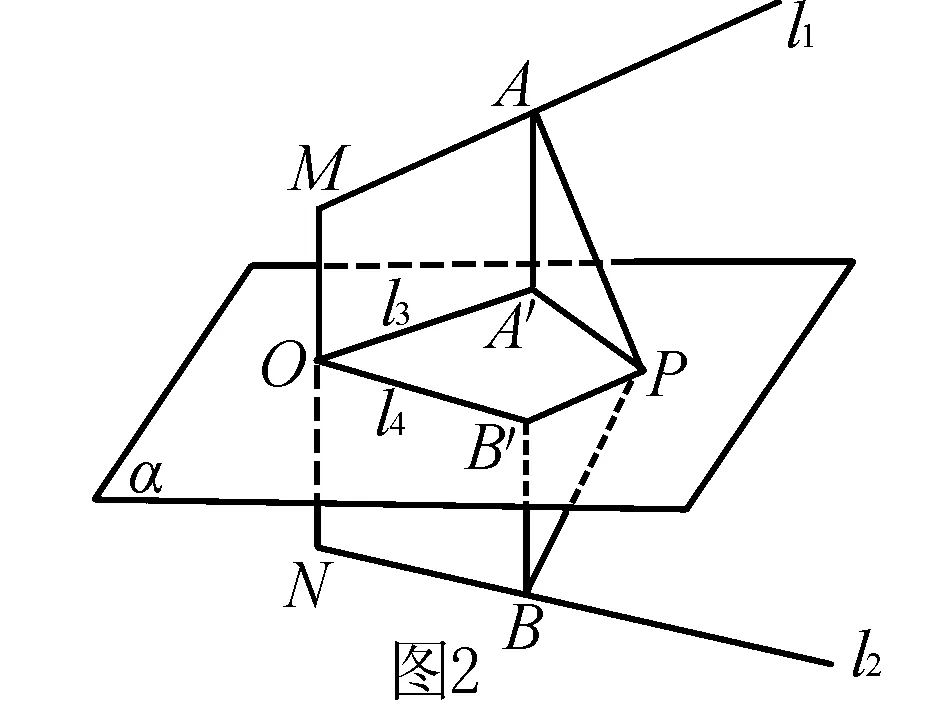
解 如图1，设MN为l1、l2的公垂线段，交平面α于点O．因为l1、l2与α平行且距离相等，所以点O为MN的中点，且MN⊥平面α．

设P为所求轨迹上的一点，则P到l1、l2的距离PA、PB相等．设MA、MO确定的平面与α的交线为l3，则l3必过O点．在此平面内作AA′⊥l3，则AA′⊥平面α，故PA′为PA在平面α内的射影．由l1∥l3得AP⊥OA′，根据三垂线定理的逆定理知，PA′⊥l3．再设NB、NO确定的平面与α的交线为l4，在此平面内作BB′⊥l4，同理可证PB′⊥l4(PB′为PB在平面α内的射影)．∵AA′=BB′，PA=PB，∴PA′=PB′．∴P点的轨迹是∠A′OB′及其外角的平分线．故平面α上与l1、l2距离相等的点的轨迹是两条相交直线．

点评 以上几例都是通过题目中的线面位置关系得出一些容易判定的等式，从而确定动点的轨迹，其基本策略就是将空间问题“平面化”．

二、利用曲线的定义确定动点的轨迹

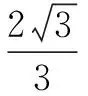
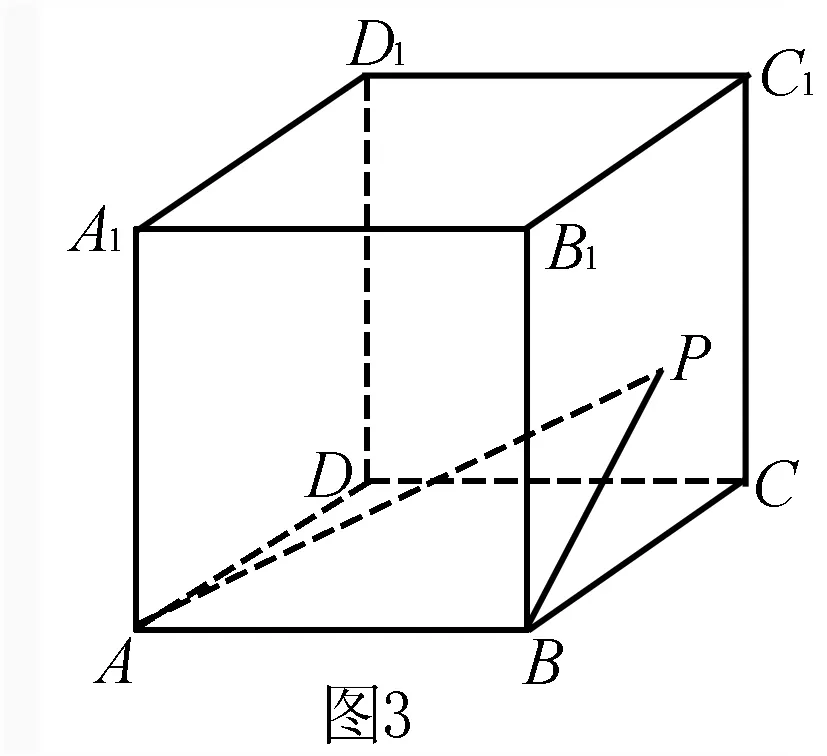
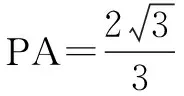
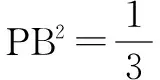
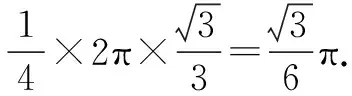
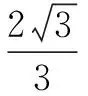
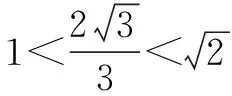
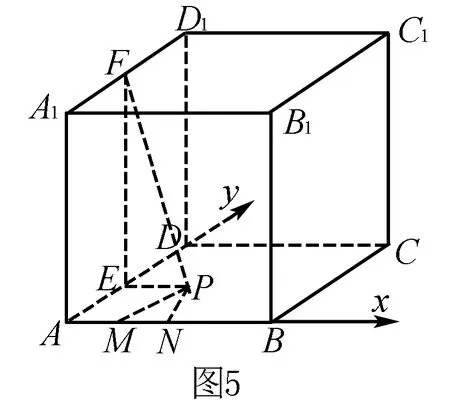
例4 如图3，在正方体ABCD-A1B1C1D1中，P是侧面BCC1B1内一动点，若P到直线BC与直线C1D1的距离相等，则动点P的轨迹所在的曲线是( ).

A.直线 B.圆

C.双曲线 D.抛物线

解 连结PC1，在正方体中，由D1C1⊥平面BCC1B1，得D1C1⊥PC1，即PC1是P到直线C1D1的距离．由题意，点P到直线BC与点C1的距离相等．故P点的轨迹是以C1为焦点，BC为准线的抛物线，选D．

变式1 把“P到直线BC与直线C1D1的距离相等”变为“P到直线BC与直线C1D1的距离之比为2∶1”，则动点P的轨迹所在曲线是椭圆．

变式2 把“P到直线BC与直线C1D1的距离相等”变为“P到直线BC与直线C1D1的距离之比为1∶2”，则动点P的轨迹所在曲线是双曲线．

点评 以上两例先仍然是由点、线、面的位置关系得出一些等式或不等式，再结合圆锥曲线的定义求解，它完全符合“在知识交汇点处命题”的高考命题原则．

三、通过建系设点转化为方程形式确定动点轨迹

A.抛物线 B.双曲线 C.椭圆 D.直线

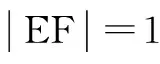
点评 对于复杂一些的空间图形中点的轨迹问题可先将有关问题转化到一个平面内，再建立平面直角坐标系，利用解析几何或代数的方法求出轨迹方程进行判断解决．

四、利用向量的方法确定动点轨迹

例7 (2016年深圳模拟)一定长线段AB的两个端点分别沿互相垂直的两条异面直线l、m运动，求它的中点的轨迹．

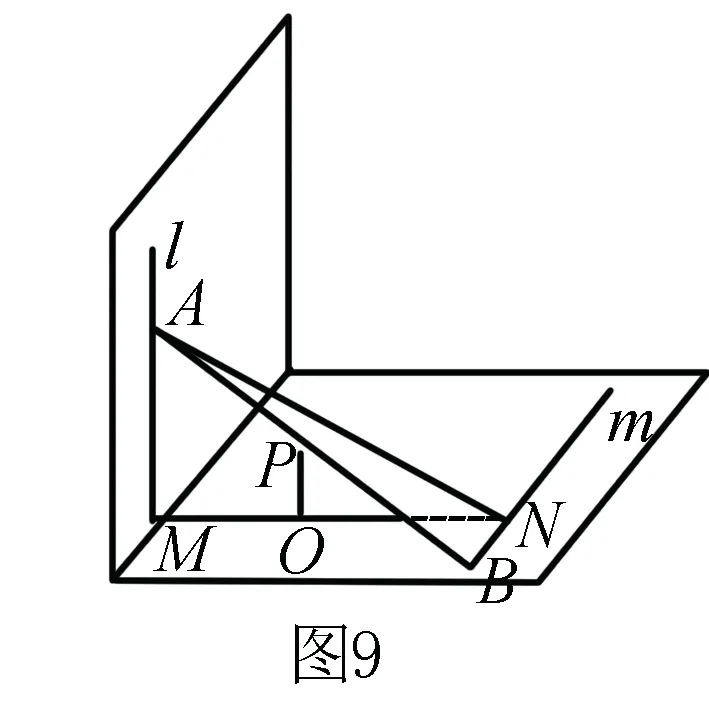
解 如图7，设MN为l、m的公垂线段，连结AN，则AM⊥MN，NB⊥MN．分别记MN、AB的中点为O、P，AB=a，MN=b，

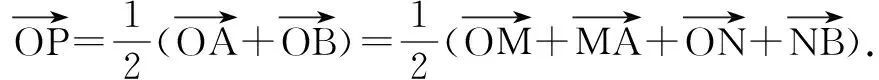
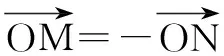
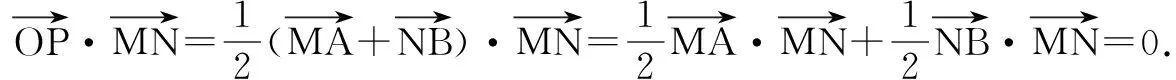
∴P点必在MN的垂直平分面上．

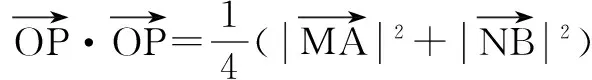
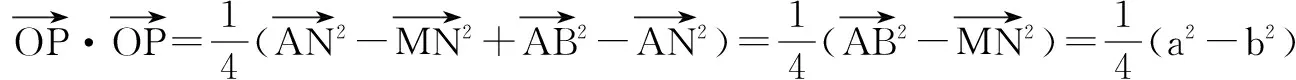
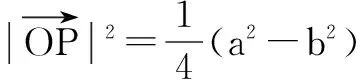
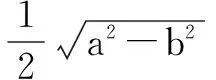
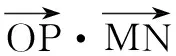
[1]王勇. 探求空间图形中的轨迹问题[J].考试(高考数学版) ,2007(2).

[2]唐永,徐秀. 聚焦“正方体”中的轨迹[J]. 中学数学,2005(07).

[责任编辑：杨惠民]

2017-05-01

吕涛(1977.10-),男，湖北当阳，大学本科，中学一级教师,从事高考研究.

G632

B

1008-0333(2017)16-0022-02