如何在高中数学教学中渗透数学思想

敬林森

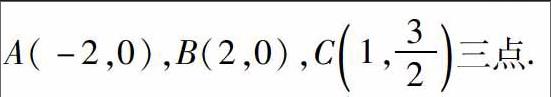
【摘要】数学思想是隐藏在数学知识体系中的无形知识，教师要通过解题向学生渗透这种思想，使学生可以在探究中形成自己的思维方式，逐步地掌握数学思想.本文主要探究了转化、分类讨论和数形结合思想的应用，以期提高学生的数学思维能力.

【关键词】高中数学；数学思想；转化；数形结合；分类讨论

常见的数学思想有转化、分类讨论和数形结合，教师要引导学生做题时多看、多想、多畫，重视学生的空间想象能力、逻辑思维能力、化归转化能力的提高.为了提高学生的数学思想意识，教师要在教学过程中点明数学思想；在试卷分析中渗透数学思想；在实践练习中运用数学思想，在无形中使数学思想可以融入学生的思维中，在润物细无声中提高学生的思维能力，掌握数学思想.

一、转化思想，转未知为已知

转化思想顾名思义就是把数学试题中的概念、公式或数量进行转化，通过已知条件和数据来求未知的数据.有些题目看似与所给条件没有任何关系，但是通过转化就会发现，所给条件正是求出未知数据的关键，只要注重使用转化思想就可以.学生要明确其中隐藏的知识规律，灵活转化，找到所给条件之间的联系，进而利用已知条件解决未知问题.例如，已知椭圆E的中心在坐标原点，焦点在坐标轴上，且经过

（Ⅰ）求椭圆E的方程；

（Ⅱ）若点D为椭圆E上不同于A，B的任意一点，F（-1，0），H（1，0），当△DFH内切圆的面积最大时，求△DFH内心的坐标.

解决第一问时，学生可以根据椭圆经过A，B，C三点，设方程为mx2+ny2=1，得到m，n的方程组，解出m，n得到椭圆方程；在解决第二问时，学生可以将△DFH内切圆的面积最大，转化为△DFH的面积最大，进而转化为点D的纵坐标的绝对值最大，此时D为椭圆短轴端点.这种转化的思想会让学生发现问题变得简单了很多，从而可以找到解题思路，在转化思想的引导下顺利地解题.计算中，学生会看到 ，

二、分类讨论，全面考虑问题

分类讨论是数学学习中的一种重要思想，二次函数、一元二次方程及一元二次不等式的综合应用，以及幂函数的图像及性质，都会涉及分类讨论思想.教师要引导学生全面地看问题，对知识分几种情况进行讨论，而不是单一地看问题.例如，试题：已知f（x）=x2+3x-5，x∈[t，t+1]，若f（x）的最小值为h（t），写出h（t）的表达式.解题中学生需注意：如图所示，函数图像的对称轴为x=-32，学生需要分几种情况来分别讨论，才能够完整地解决问题.

本题中对称轴的位置相对于区间的位置不同，就会有不同的答案.学生在分析中要把各种可能性都考虑到，同时还要对此类问题进行归纳总结，探究一般规律.学生要认识到在研究有关二次函数最值时，一般用分类讨论思想，一是对系数a进行讨论，二是要对对称轴进行讨论，在分类讨论中要遵循分类的原则：一是分类的标准要一致；二是分类时要做到不重不漏；三是能不分类的要尽量避免分类，绝不无原则地分类讨论.通过归纳，学生会更好地理解分类讨论的数学思想，进而在解题过程中灵活地应用.

三、数形结合，直观形象生动

数形结合会帮助学生更好地理解抽象的数学知识，变抽象为形象具体.在高中数学知识学习过程中，学生会发现函数知识、平面几何、立体几何、双曲线等等数学问题都可以采用数形结合的思想来解决问题.一边读题，一变化图，根据已知条件来绘图，简单直观地看到数量关系，可以更迅速快捷地解题.

总之，教师应对学生进行“授之以渔”的教学，多向学生传授数学思想和方法，引导学生学会分析数学知识规律，进而在解题过程中灵活地应用.教学中教师要善于结合试题，向学生渗透数学思想，使学生可以利用数学思想来顺利地解决问题，提高能力.