基于Kriging模型的快速拆装叶轮轮盘多目标优化设计

冀春俊 徐浩 孙琦 孙淼

（大连理工大学能源与动力学院）

基于Kriging模型的快速拆装叶轮轮盘多目标优化设计

冀春俊 徐浩 孙琦 孙淼

（大连理工大学能源与动力学院）

为了降低叶轮安装端面变形量以及减轻叶轮质量，对快速拆装形式的叶轮轮盘结构进行多目标优化设计，使用拉丁超立方试验设计和有限元分析生成初始样本数据并构造出Kriging近似模型，运用遗传算法对近似模型进行寻优。对优化后的参数值进行工程取整并进行有限元分析得出叶轮轮盘结构设计模型，最终优化结果显示叶轮质量减小了15%，叶轮摩擦端面轴向变形量降低了29%。优化后的叶轮模型可提高拉杆螺栓连接转子结构的可靠性。

快速拆装叶轮；优化设计；Kriging模型

0 引言

离心压缩机在石油、化工和造纸等国民生产领域中有着广泛应用。随着离心压缩机向着小流量、高速化方向发展，对叶轮提出越来越高的设计要求，叶轮结构设计的好坏直接影响着整个机组的可靠性[1]。在现代高性能叶轮设计中，优化设计是必不可少的工作，由于离心叶轮的叶片形状设计是在气动设计中完成，因此对叶轮形状设计主要针对轮盘。目前对离心叶轮进行结构优化主要是降低应力、减轻质量和整体变形量，此外对不同安装形式的叶轮其装配工艺的优化同样重要[2]，但是这些方面又存在相互制约的关系，因此有必要使用优化设计的方法来平衡设计之间的冲突。

Kriging模型的数学思想是在20世纪初随着经典统计学理论逐渐形成的，第一次成功运用是地质学家DanieKrige进行地质情况模拟及矿产分析。Kriging代理模型由线性回归部分和非参数部分组成，它较单个的参数化模型更具有灵活性，同时克服了非参数化模型处理高维数据而存在的局限性[3]。目前，Kriging模型作为一种有效的近似技术已经广泛应用在结构优化、多学科优化设计、航空设计等工程优化设计领域。

本文运用Kriging模型-遗传算法对某压缩机离心叶轮轮盘进行形状优化设计，选择叶轮质量和摩擦端面的轴向变形量最小为优化目标[4]，约束条件为叶轮最大应力和叶顶变形量。优化后的叶轮在叶轮应力和叶顶变形量符合要求的情况下质量得到减轻，摩擦端面变形量大幅减少，对整个转子运转的可靠性有着积极的影响。

1叶轮结构描述

快速拆装叶轮是利用一个两端带螺纹的拉杆来连接叶轮与轴，连接结构如图1所示。在安装过程中，先用液压工具将拉杆产生弹性变形拉长，然后拧紧锁紧螺母，在液压卸除后，将叶轮紧紧压在轴的端面上，从而产生非常大的摩擦力，这个摩擦力在整个转速范围内都能保证叶轮与轴不会发生松动[5]。当叶轮需要拆卸时，先用液压工具将拉杆拉长，然后松开锁紧螺母，卸除液压后叶轮可与轴分离，整个过程实现快速拆装。

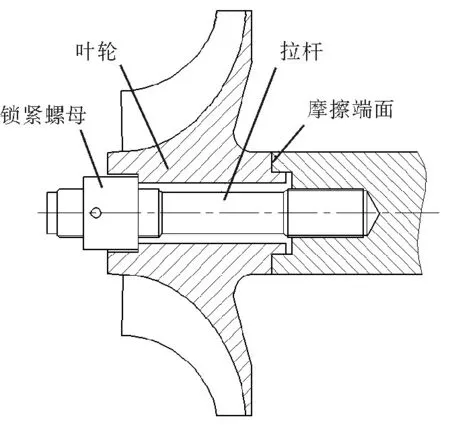
图1叶轮连接结构图Fig.1Impeller connecting structure

本文研究的叶轮为某单级高速直驱压缩机主要零件，叶轮通过拉杆螺栓直接与高速电机轴相连接，通过端面摩擦将电机扭矩传递给叶轮，叶轮由7A09铝合金加工而成，工作转速20 000r/min。在高速旋转时叶轮受到离心力的作用会产生一定的变形量，叶轮整体变形趋势为朝向进口方向。对于快速拆装形式的叶轮，摩擦端面的轴向变形会减弱螺栓预紧力造成接触面的分离，因此对此类结构形式的转子，叶轮合理的结构设计和拉杆螺栓预紧力的准确计算是保证整体结构安全可靠的关键。

2优化设计

2.1Kriging近似模型

Kriging模型是一种估计方差最小的无偏估计模型，能够很好地逼近具有非线性特征的复杂问题。在计算过程中，Kriging代理模型计算量小同时计算结果与高精度复杂模型接近，在优化设计中使用代理模型可以提高优化效率，降低计算成本[6]。

对选定p个训练样本空间

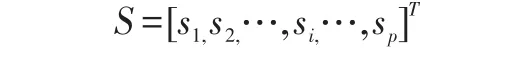
训练样本所对应的p个实际响应值向量

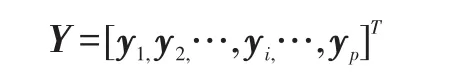
那么用Kriging代理模型来描述第i个训练样本的模拟响应向量ŷi(x)

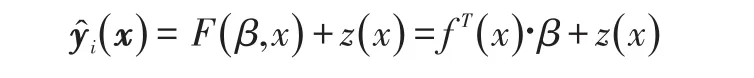
其中，F(β,x)为回归模型部分；z(x)是模型非参数部分相关函数；z(x)服从正态分布，其均值为0，方差σ2，训练样本点之间协方差

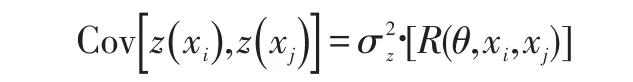
θ是高斯相关函数的关键参数，通过优化θ能够自适应调节设计点之间的相关性

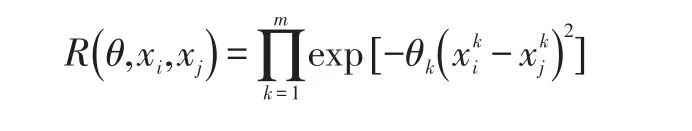
相关函数确定以后，就可以建立观测点的模拟响应值ŷ，关于待测点的表达式

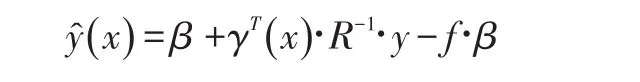
建立Kriging近似方程后，常用的近似模型检验方法有复相关系数（R2）、修正的复相关系数（adjustedR2）、均方根误差（RMSE）等。

2.2设计变量的选择

离心叶轮在不改变叶片形状只对轮盘进行优化时

的轮盘截面形状及设计参数如图2所示。

图2 轮盘结构优化设计参数Fig.2Design parameters of wheel structure

设计参数P1为轮盘靠近叶轮出口处厚度值，P1减小可降低叶轮惯性载荷，P1增大可改善叶根应力值。

设计参数P2为锥部斜线与垂直面夹角，P2对减轻叶轮质量，降低叶轮离心载荷，保证叶轮出口处刚度起到较重要作用。

设计参数P3为控制锥部位置的参数值，P3对叶轮应力以及质量有重要影响。

设计参数P4为轮盘背面锥部倒圆角，P4对改善叶轮应力分布，减轻质量，改善轮心处应力状况有一定作用，但是如果此处选择不当易形成高应力区。

设计参数P5为叶片根部倒圆角值，P5对叶根应力值有较大影响。

各设计参数相应的初值及取值范围如表1所示。

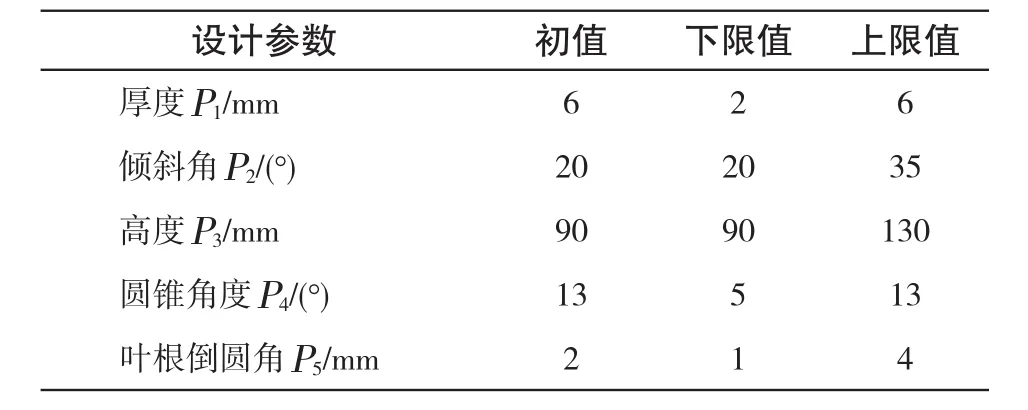
表1 设计参数变化表Tab.1Design parameter variation

2.3 优化过程

在对叶轮进行多目标优化时利用三维建模软件SolidWorks建立起叶轮关于设计变量的参数化模型，通过ANSYS Workbench平台与SolidWorks之间的连接接口实现数据传递。采用拉丁超立方进行试验设计并对试验点进行有限元分析从而得到一组样本点，利用样本数据建立起Kriging近似响应面模型。对模型精度进行分析，当构建的近似模型满足精度要求时采用遗传算法进行寻优得到Pareto最优解，对得到的最优解进行数值圆整处理，从而得到最终的叶轮优化形状。快速拆装叶轮轮盘结构多目标优化流程如图3所示。

图3 叶轮轮盘多目标优化流程图Fig.3Multi objective optimization process of impeller disc

由于叶轮叶片形状已经在气动设计中完成，因此，本文优化主要针对轮盘背部形状进行。对于拉杆装配连接的叶轮在高速状态下工作时，会出现摩擦端面距离变短的情况，这将减弱拉杆预紧力，造成叶轮与轴脱离，计算中应考虑叶轮摩擦端面的轴向变形量[7]。本文优化设计目标确定为叶轮整体质量最轻及叶轮摩擦端面的轴向变形量最小。

根据本文叶轮的安装形式，进行有限元分析时对叶轮与锁紧螺母连接的部位进行全约束，对叶轮摩擦端面处约束周向位移，对叶轮整体施加惯性载荷。由于叶轮形状具有周期对称性，本文叶轮叶片数13个，因此选取叶轮1/13扇区作为计算对象，叶轮单扇区三维模型及边界条件设置如图4所示。

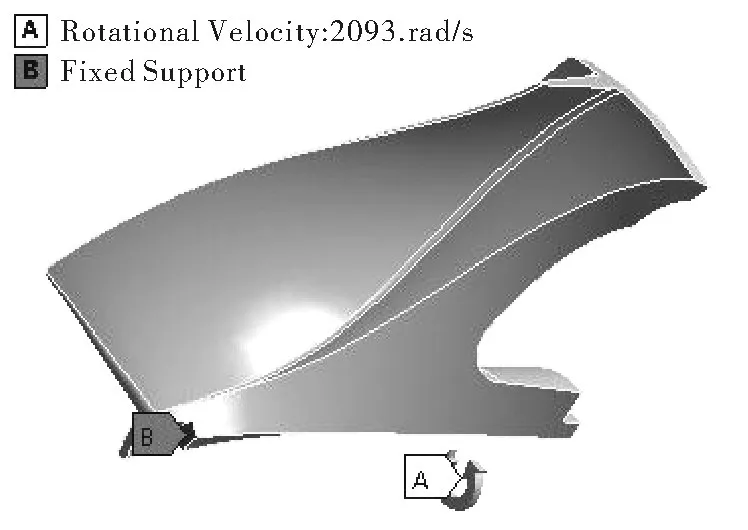
图4 叶轮三维计算模型及边界条件设置Fig.43D calculation model and boundary conditions of impeller

2.4 优化过程数学模型

优化设计问题的数学模型：

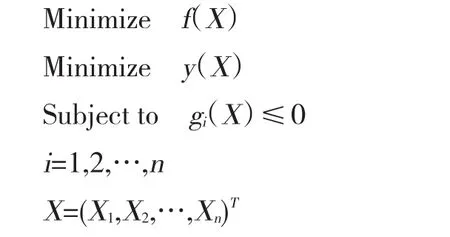
式中，f和y为目标函数；X为设计变量；gi为约束条件。

在本文中目标函数为叶轮质量和叶轮摩擦端面轴向变形量最小，约束函数为叶轮应力不超过材料许用应力值350MPa，叶顶轴向变形量不超过0.5mm。

3 叶轮轮盘多目标优化设计及结果分析

3.1 叶轮轮盘结构多目标优化

优化过程中常用的试验设计方法有中心复合设计、均与设计、正交设计和拉丁超立方设计等。本文采用拉丁超立方试验设计的方法对叶轮结构5个设计变量进行20次试验设计，在有限元分析模块中对这些试验样本进行计算，得到初始样本数据点。选择Kriging近似模型方法拟合样本数据，建立起近似响应面模型。

对于多目标优化问题在优化过程中会根据优化问题的目标函数构成一个适值函数，对一个或多个解构成种群进行评估分析，因此多目标优化得出的结果是多个最优解组成的集合，一般称为Pareto最优解。在Pareto最优解集中任意两个解不能直接对比其优劣性，如何再进行选择要看实际问题的需要[8]。

本文采用多目标遗传算法MOGA进行寻优，MOGA是基于NSGA-II（非支配排序遗传算法-Ⅱ）的一个变种。它支持多种目标和约束找到全局最优。一个迭代的多目标遗传算法，提供比筛选一个更精确的方法，非常适合用于计算全局最大最小值，同时可以规避局部最优的陷阱[9]。优化设计时设定初始种群数为1 000，最大迭代数为20，优化计算获取3个最优方案。

3.2 优化结果及分析

利用上述优化方法进行优化设计后得到3组优化方案，各方案参数结果及叶轮力学性能见表2和表格3。

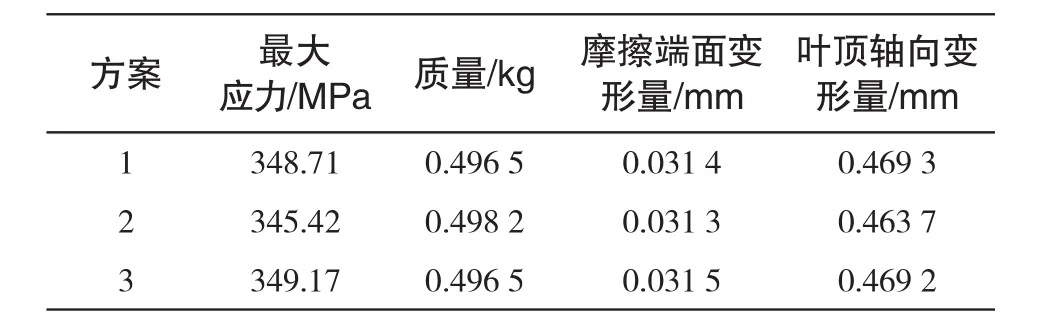
表3 叶轮轮盘结构多目标优化叶轮性能结果Tab.3Performance of multi objective optimization impeller disc structure

从表2和表3中可以看出3个优化方案数值比较接近，但优化后的参数值不能为工程所应用，从生产加工角度对优化方案中各参数进行数值圆整处理，并进行有限元分析从而得到最终优化方案的结果。对比最终优化方案与叶轮原始方案的设计参数和有限元计算结果如表4和表5所示。从表5可以看出最终方案与优化得到的3个方案结果相差不大，这种再次进行有限元分析的方法可以检验出本文构建的Kriging近似模型精度较好，满足真实情况。

表4 优化前后叶轮结构尺寸对比Tab.4Comparison of impeller structure size before and after optimization

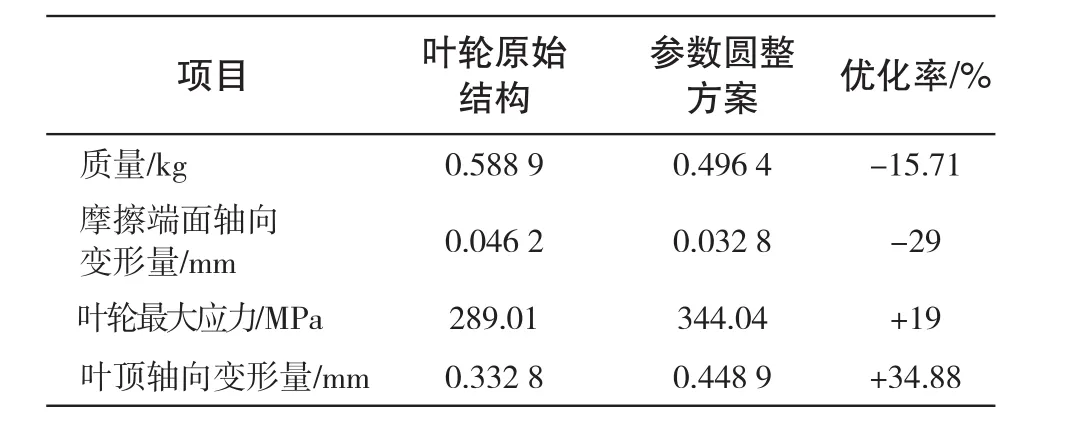
表5 叶轮优化前后结果对比Tab.5Comparison of results before and after optimization

由表5可以看出通过多目标优化设计后的叶轮单个通道的质量较原始叶轮单通道质量减轻了15.71%，实现了叶轮减重的目标。叶轮摩擦端面轴向变形量如图5，最大轴向变形量为0.032 8mm比原始结构减少29%，提高了工艺装配的稳定性，同时对拉杆预紧力设计提供了数值依据。

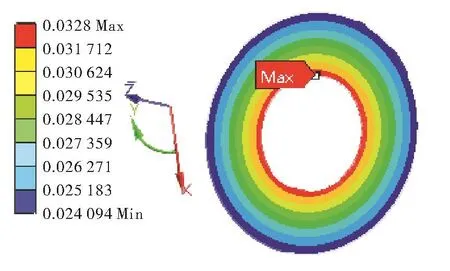
图5 摩擦端面轴向位移云图Fig.5Axial displacement contour of friction end-face

叶轮应力结果如图6，最大等效应力值为344MPa出现在叶片根部靠近出口位置，叶顶轴向变形量如图7，叶片顶部最大轴向变形量为0.448 9mm。叶轮最大

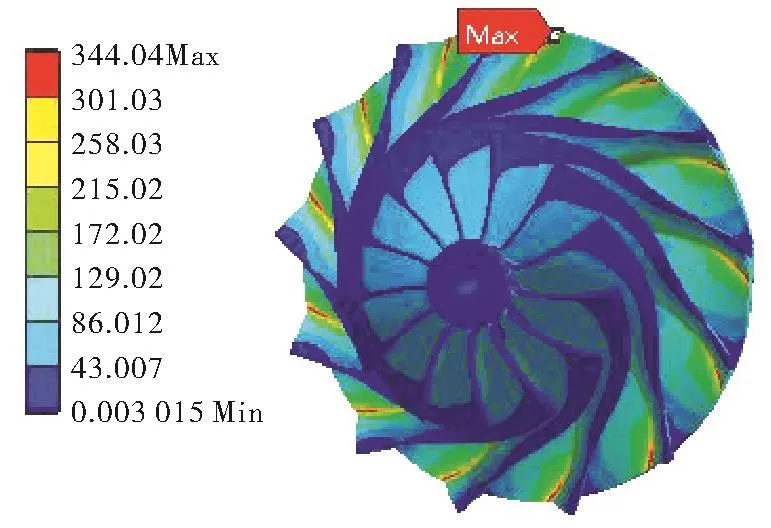
图6 优化后叶轮应力云图Fig.6Stress contour of optimized impeller

4 结论

本文对快速拆装这一结构形式的叶轮作为研究对象，提出叶轮质量和叶轮摩擦端面变形量为目标函数，叶轮最大应力和叶顶变形量为约束条件的多目标优化。优化过程为采用拉丁超立方进行试验设计获得样本点，通过样本点构造出Kriging近似响应面模型，对Kriging模型运用遗传算法进行优化。

通过Kriging模型-遗传算法优化的方法能有效减少设计样本点的选取数量，提高优化设计效率。对优化后的数值进行取整后得到最终优化方案，与原始结构相比优化后叶轮质量减小了15.71%，叶轮摩擦端面轴向变形量减小了29%。叶轮质量减小后在高速旋转状态下离心力减小，结构安全性得到提高。叶轮摩擦端面变形量减小对拉杆螺栓预紧力的影响变小，叶轮与轴接触面连接更加可靠。应力值和叶顶轴向变形量较叶轮原始结构均有所增大但都在约束范围内。

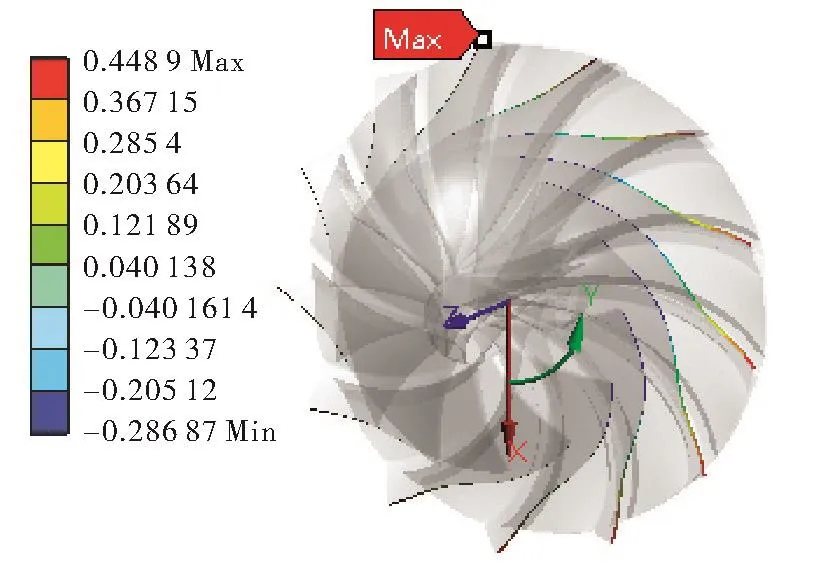
图7 叶顶轴向位移云图Fig.7Axial displacement contour of tip

[1]James M.Sorokes,MarkJ.Kuzdzal,张海界.离心压缩机的发展历程[J].风机技术,2011（3）：61-71.

[2]王睿,王跃方.通风机转子过盈装配松脱转速数值分析[J].风机技术,2017（1）：38-42.

[3]赖喜涛,温卫东,冯大俊.基于Kriging模型的离心叶轮结构优化设计[J].沈阳航空航天大学学报,2014（4）：17-22.

[4]冀春俊,高亚威,孙琦，等.基于ANSYS的离心风机叶轮结构优化研究[J].风机技术,2016（6）：49-52.

[5]冀春俊,仵忠浩,张晨阳,等.一种离心式风机及用于连接其叶轮和转轴的连接装置[P].黑龙江：CN104929975A,2015.

[6]李飞.代理模型预测研究及其在叶轮机械中的应用[D].大连理工大学,2014.

[7]关振群,罗阳军,王学军,等.离心式叶轮三维参数化形状优化设计方法[J].机械强度,2006（6）：833-838.

[8]唐明裴,阎贵平.结构灵敏度分析及计算方法概述[J].中国铁道科学,2003（1）：76-81.

[9]陈国栋.基于代理模型的多目标优化方法及其在车身设计中的应用[D].湖南大学,2012.

Multi-objective Structure Optimization of a Fast Disassembling Connection Impeller Disk Based on Kriging Model

Chun-jun JiHao XuQi SunMiao Sun
(School of energy and Power Engineering,Dalian University of Technology)

In order to improve the installation reliability and reduce the weight of impeller,a multi-objective optimization method was used for the fast disassembling connection impeller disk structure.The initial sampling data was obtained and a Kriging model was constructed by a latin hypercube sampling design and a finite element method.A genetic algorithm was applied for global optimization.The optimized design parameters were obtained by a finite element analysis for the impeller wheel structure.After the optimization,the weight of impeller was decreased by 15%,the axial deformation of the impeller friction section was decreased by 49%.The optimized impeller model can improve the reliability of the rod bolt which connects the rotor structure.

fast disassembling connection impeller，optimal design，Kriging model

TH452；TK05

1006-8155-(2017)03-0044-05

A

10.16492/j.fjjs.2017.03.0008

2016-12-20辽宁大连116024