麻灰纱中色纤维混合模型运用

程 璐，马崇启，王玉娟，刘建勇

(天津工业大学 纺织学院，天津 300387)



麻灰纱中色纤维混合模型运用

程 璐，马崇启，王玉娟，刘建勇

(天津工业大学 纺织学院，天津 300387)

针对目前大部分色纺企业仍然依靠有经验的配色人员进行人工配色，存在配色效率低、配色精度差等问题，提出运用反向传播(BP)神经网络的方法对色纺纱的黑白纤维混合配色进行预测，并与使用Datacolor MATCH系统模拟染料配色方法和基于颜色混合模型中的Kubelka-Munk双常数理论的配色方法对黑白纤维混合配色的结果进行对比。结果表明：上述3种方法均可对麻灰纱的黑白纤维混合配色进行有效的预测，配方的相对误差基本控制在7.36%之内，且配方样品与标准样品的色差小于1；比较而言，3种黑白纤维混合配色的预测模型中，基于BP神经网络的配色方法适用性及精度最佳，配方的相对误差最高，为3.08%。

麻灰纱；配色方法；模型；Kubelka-Munk双常数理论

在染整行业，染料的配色无论在理论上还是实际应用方面，都有着几十年的发展历史，技术也相对成熟。然而，色纤维的颜色混合模型主要是参照颜色混合理论，包括Kubelka-Munk双常数理论模型[1]、Friele模型[2]和Stearns-Noechel模型[3]。之前研究发现，三者在色纤维混合配色方面的平均CIELAB色差分别为1.6、2.7、2.4[4-5]，色差最小效果最好的明显是Kubelka-Munk双常数理论模型，但在实际应用方面还存在一定的问题。国内的理论研究主要是在以上理论的基础上进行算法改进[6]，在应用方面的研究报道不多。目前，国内大多数色纺纱行业的配色仍然依靠人工进行，大大地降低了该产品的生产效率，同时也阻碍了色纺纱技术的进步。本文研究主要从黑色纤维与白色纤维的混合着手分析混合模型，试图用颜色混合模型以及新的数学的方法进行黑白纤维的配色，为计算机配色提供一定的理论基础。

1 麻灰纱样品的制备与测试

1.1 实验原料及仪器

将黑色粘胶纤维与白色粘胶纤维通过不同比例进行混纺，其中基础数据中黑色纤维比例范围在0～100%之间，共制备32组样品，如表1所示。

实验仪器：XFH型小和毛机、DSCa-01型数字式梳棉试验机、DSDr-01型数字式并条机、DSRo-01型数字式细纱试验机、Y381A型摇黑板机、Datacolor SF600型分光光度仪。

1.2 制样方法

采用摇黑板机将纱线缠绕制成纱板，纱线板的规格为6 cm×22 cm。将样品缠绕在纱线板不但减少了纺制成织物的工作量，而且颜色值不受织物的组织结构、厚度等参数的影响；另外，细纱板与纤维网、纤维条和粗纱相比，可更好地反映混色纱的色彩效果。

表1 混色纤维比例Tab.1 Proportion of blended fibers

1.3 测色方法

使用Datacolor公司生产的Datacolor SF600分光光度仪进行测色，选择大孔径、10°视角、不包含镜面光泽、100%紫外线滤光，在D65标准光源下进行测量，每个样品测量8次，每次测量移动样品的位置并且旋转90°，最后记录该色样的35个反射率值(波长范围为360～700 nm，记录间隔为10 nm)以及三刺激值(X、Y、Z)。

2 Datacolor MATCH软件配色

2.1 数据库的建立

参照染料配色的原理，将混纺纱的反射率等颜色值保存在Datacolor公司研发的Datacolor MATCH系统中，建立一组浓度梯度数据库供配色时使用。为确保实验的准确性，选取9组混色样品，如表2所示。不同混色样的反射率曲线如图1所示。在此基础上依据数据库，使用测配色系统对混色样品进行测色并且计算出混色样品的配方。

表2 Datacolor MATCH配色系统基础数据库Tab.2 Database used by Datacolor MATCH system

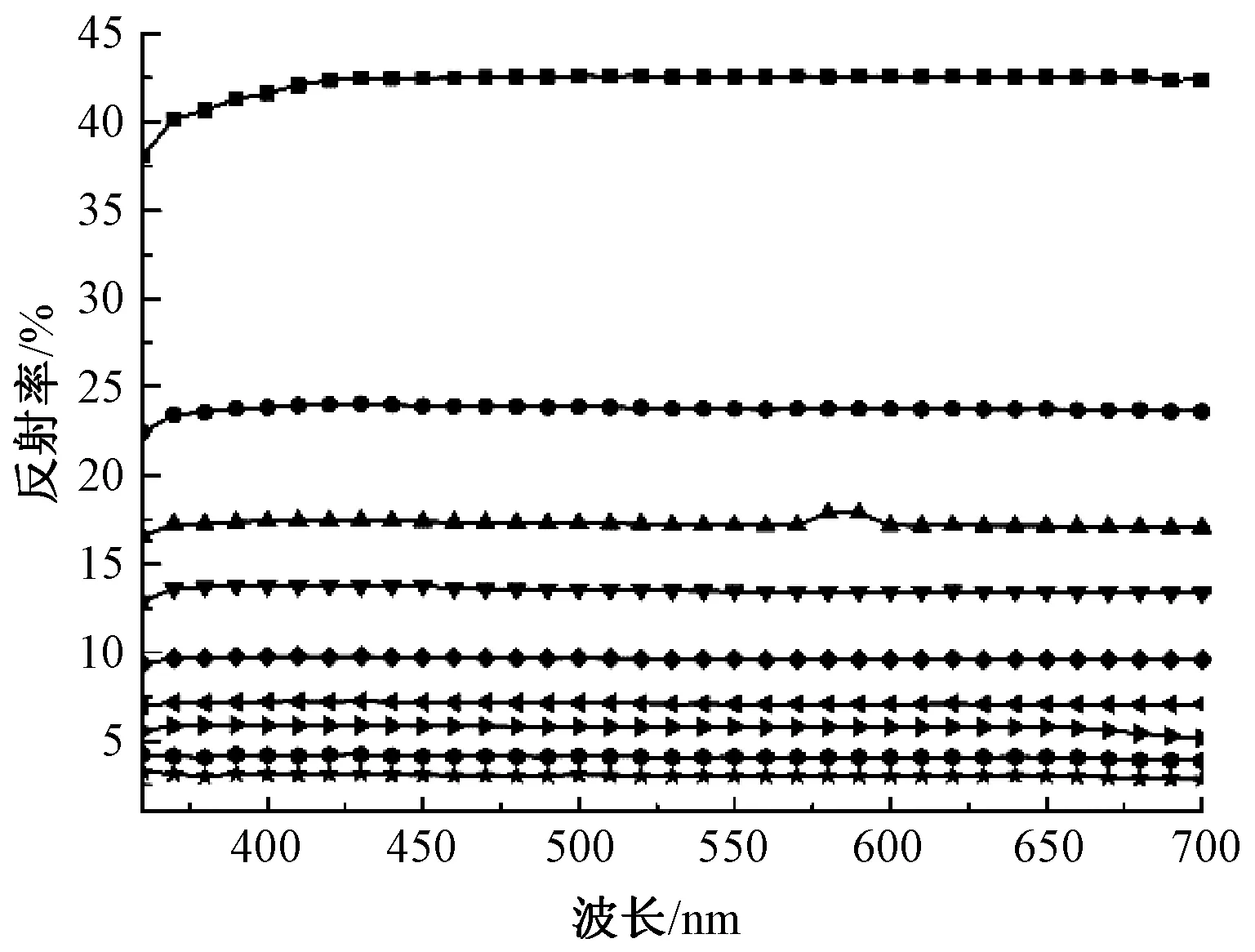
注：图中曲线由下至上依次为试样4、7、9、14、17、21、24、27、31。图1 麻灰纱不同黑色纤维比例的纱线反射率Fig.1 Reflectance of gray yarns containing different proportions of black fibers

2.2 实验结果

通过测试若干组样品的颜色参数值，Datacolor MATCH软件内部给出的配方如表3所示。

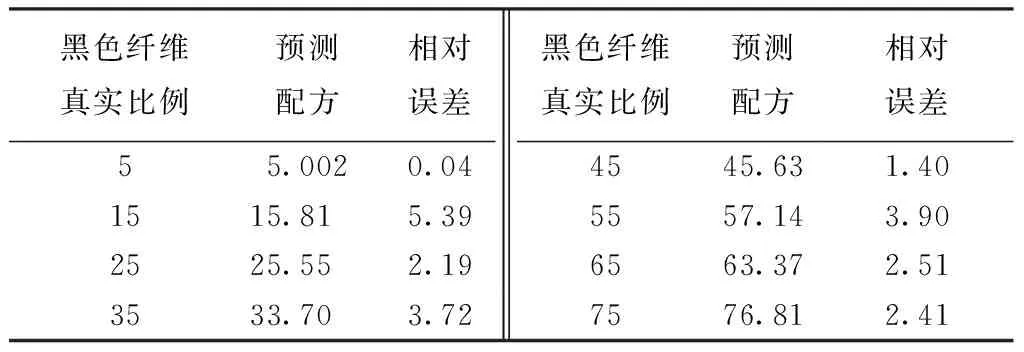
表3 Datacolor MATCH软件配色结果Tab.3 Prediction formula provided by Datacolor MATCH %

由表3可知，该软件在计算麻灰纱的配色方面有较好的结果，其黑色纤维的配色误差控制在0～5.39%范围内，说明该软件在2种纤维混合的配色方面有一定的适应性，即染料的混合配色模型和有色纤维混合配色模型在一定程度上都适用于Kubelka-Munk理论模型。

3 Kubelka-Munk双常数理论预测配方

3.1 Kubelka-Munk双常数理论

本文使用Kubelka-Munk双常数理论对黑白粘胶纤维混合进行研究，并且结合最小二乘法计算单色纤维配比，从而实现全光谱匹配。下面简要介绍Kubelka-Munk理论[7]。

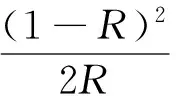
(1)

式中：R为某样品在不同波长下的反射率，%；K/S为有色纤维的吸收系数与散射系数的比值。

根据Kubelka-Munk双常数理论：

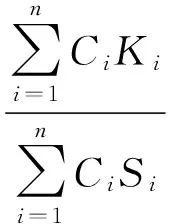
(2)

式中：(K/S)m为混色纱线的K/S值；Ci为第i种单色纤维的质量比例；Ki为第i种单色纤维的吸收系数；Si为第i种单色纤维的散射系数；n为混色纤维的颜色数量。

若是2种纤维混合，则：

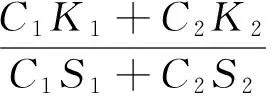
(3)

将方程进行移项整理：

-C1K1-C2K2+C1S1(K/S)m+C2S2(K/S)m=0

(4)

式中：K1、K2分别为白色粘胶纤维和黑色粘胶纤维的吸收系数；S1、S2分别为白色粘胶纤维和黑色粘胶纤维的散射系数；C1、C2分别为在混色纱线中白色粘胶纤维和黑色粘胶纤维所占的质量比例。式(4)中有K1、K2、S1、S24个变量，在理论上有4个方程便可求出此解，但为得到更加精确的解，取方程数大于4，并且采用最小二乘法求出方程的逼近解，即单色纤维吸收系数K和单色纤维散射系数S，然后根据求得的K、S值和样品的K/S值反推，求得样品的配方[8]。

3.2 实验结果

当使用式(4)并结合最小二乘法计算单色纤维的吸收系数和散射系数时，方程数量的不同和单色纤维所占质量比的不同都有可能影响最终计算结果。为得到更加精确的结果，本方程选取尽可能多的比例求解，同时这些比例可覆盖较大的范围，因此基础数据库采用的白色粘胶纤维与黑色粘胶纤维的质量比分别为10∶0、9∶1、8∶2、7∶3、6∶4、5∶5、4∶6、3∶7、2∶8、1∶9、0∶10，利用这11组麻灰纱先求出黑色纤维与白色纤维的K、S值，然后再次根据已知混色纱线的K/S值和单色纤维的K、S值，反推出几组麻灰纱的配方，结果如表4所示。

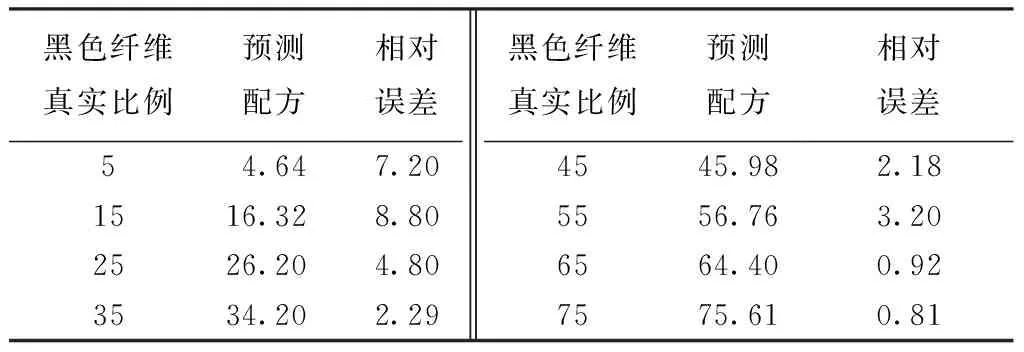
表4 基于Kubelka-Munk双常数理论预测配方Tab.4 Prediction formula based on Kubelka-Munk two constant theory %

从表4数据可知，当黑色粘胶纤维所占的比例为15%时，通过模型计算出的黑色粘胶纤维所占比例差异较大。为保证配方的准确性，从表3中选取相对误差最大的一组麻灰纱，即黑色粘胶纤维质量比例为15%时，依据预测配方纺制黑色粘胶纤维与白色纤维比例为16.32∶83.68的纱线，然后与黑色粘胶纤维为15%的样品进行对比求色差，其CIELAB总色差为0.65，小于1，色差在可接受范围内[9]。故认为此方法在2种色纤维混纺方面得到很好的配方结果，且该方法可拟合出单色纤维的吸收系数和散射系数，从而实现3种及3种以上色纤维的混合配色。

4 基于BP神经网络的麻灰纱配色

现阶段已有学者将神经网络应用到不同彩色空间之间的颜色转换，并提出了适用于色彩匹配的方法[10]。本文提出建立3层BP神经网络模型实现麻灰纱的配色，来探索并验证该数学模型在色纺纱配色中的实用价值。此模型在MatLab软件中实现，其中BP神经网络结构模型的设计如图2所示，图中Xi、Yi、Zi为试样的三刺激值。

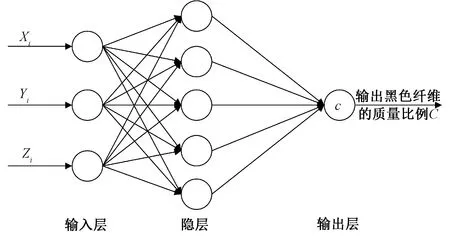
图2 BP神经网络的结构模型Fig.2 Structure model of BP neural network

4.1 网络的训练过程

4.1.1 输入层与输出层设计

输入层的选择可为样品在不同波长下的反射率或者样品的三刺激值等，因为考虑到样品的有限性，本文选择样品的三刺激值Xi、Yi、Zi，即输入层的神经元数为3，网络训练数据选取27组不同比例混纺的麻灰纱的三刺激值，黑色粘胶纤维的质量比例从0～100%，并进行归一化处理。

隐层的确定依据如下。

1)利用经验公式确定初始的隐层神经元数[11]，进行网络训练以及测试。

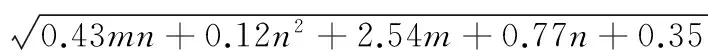
(5)

式中：s为隐层节点数；n为输出层节点数；m为输入层节点数。

2)结合MatLab试运算。在这里n=1,m=3,代入式(5)计算，将计算值四舍五入取整后，得到隐层的初始节点数为4。但在实际应用中往往节点数要多于4[12]，经过MatLab实验测试，当隐层节点数为5时，其实际值与预测值之间的相关系数最大，于是最终确定隐层节点数为5。输出层为单色纤维所占的比例，即设定为1，因此可建立3-5-1的BP神经网络模型。

4.1.2 模型训练过程

将经过归一化处理的数据进行网络训练，设计训练步长为20 000，学习速率为0.001，允许误差为0.000 1，其训练过程曲线如图3所示。由于BP神经网络在批量处理训练时易陷入局部最小且学习过程振荡，所以需要在调整权值阈值时引入动量因子[13]。

图3 BP神经网络训练误差曲线Fig.3 BP neural network training error curve

4.2 预测结果

首先，测试网络训练的正确性。对27个样本27×3个三刺激值进行网络训练，训练迭代次数为20 000，实现网络收敛，其输出值(Y)与目标值(T)的回归曲线(Y=0.99T+0.001 9)如图4所示，与斜率为1的直线Y=T基本重合，说明线性关系较好。

然后，测试BP神经网络泛化的能力。提取没有参与训练过程的另外5组样品的三刺激值进行预测，得到对应的预测值。通过多次的反复训练，选出预测结果最优时对应的权值阈值，将其保存，进而预测最终的配方，并与以上几种配色方法计算的结果进行对比，其预测结果如表5所示。

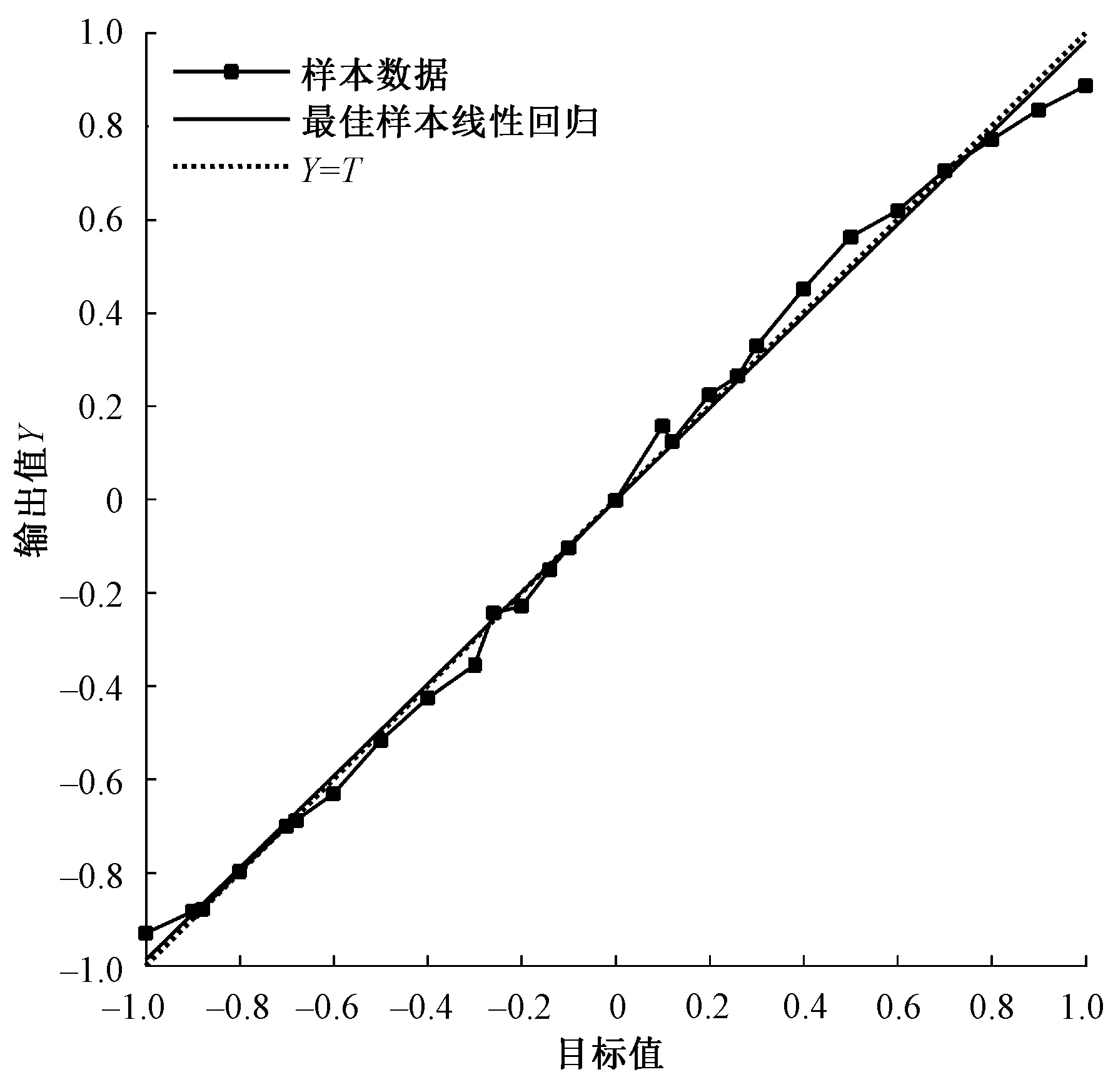
图4 BP神经网络训练输出值与目标值回归曲线Fig.4 Regression curve between BP neural network training output value and target value

由表5数据可知，相比于其他的配色方法，神经网络模型预测法在2种纤维混合所纺纱线方面得 到了较好的预测结果，可满足配色需求，且方法便捷，对于3种及3种以上的色纤维的混合也有着可观的应用前景，并且随着训练数据库的增加，网络训练精度会随之增大，预测准确度将随之增大，是一种具有长远应用价值的数学方法。但是，这种数学方法也存在一定的提升空间，比如学习过程常常发生振荡，收敛速度较缓慢，结合其他算法对神经网络进行改性也不失为一种解决途径。

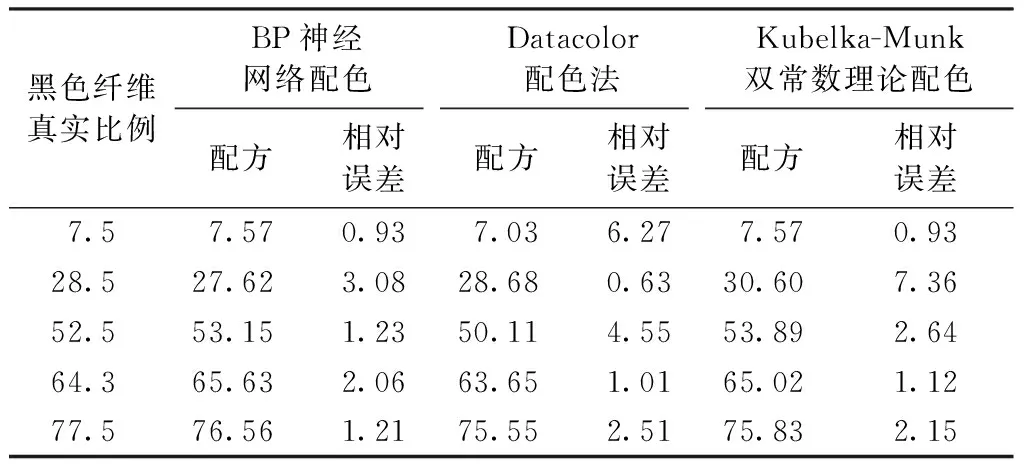
表5 几种不同预测方法的配色结果Tab.5 Predicted results of several different color matching methods %

为更直接地表征以上几种方法配色的精确性，从以上几种方法给出的配色结果中，选取相对误差较大的组合，按照配方制作样品，使用Datacolor测色仪对标准样和纺样测色对比CIELAB总色差和CMC(2∶1)色差，结果如表6所示。

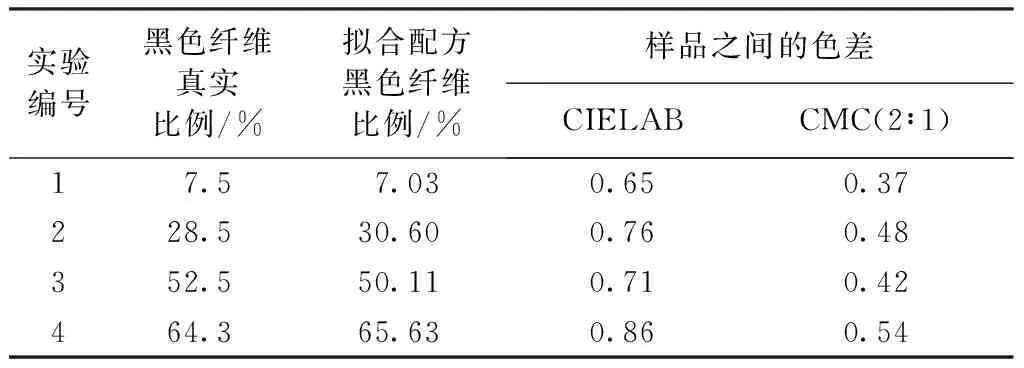
表6 预测配方与标样的色差Tab.6 Color differences between samples and formula

标准样品与配方样品的色差一方面源于算法内部的误差，另一方面是由于实验操作带来的误差。但整体来说，色差在可接受范围之内，除小比例色纺纱的配色较难控制之外，通过进一步地严格控制实验操作，可基本满足企业的生产需要。

5 结 论

在2种色纤维的混合方面，BP神经网络、Datacolor配色和Kubelka-Munk双常数配色方法均能得到很好的应用，但是，也有区别之处，比如说Datacolor配色系统能模拟染料的配色对2种纤维混合进行配色，在多种彩色纤维的混合方面适用性有待进一步的验证，但从另一方面验证了色纤维混合的理论模型与色料的混合模型存在相似之处；基于Kubelka-Munk理论的最小二乘法误差较大，但是由于该方法能拟合出单纤维的吸收系数和散射系数值，可实现多种纤维的混合配色；而基于BP神经网络的配色方法适用性及精度最好，并且具有较广的应用前景，值得进一步的深入研究。

FZXB

[1] AMIRSHAHI S H.Applying the Kubelka-Munk equation to explain the color of blends from pre-colored fibers[J].Textile Research Journal, 1994, 64 (6):357-364.

[2] PHILIPS-INVERNIZZI B,DUPONT D, CAZE C. Formulation of colored fiber blends from Friele′s theoretical model[J]. Color Research and Application,2001,27(3):191-198.

[3] LI Rong,SONG Yang, GU Feng.Color matching for fiber blend based on Stearns-Noechel model[J]. Journal of Donghua University, 2006, 4(23):17-20.

[4] DOMINICK A Burlone.Theoretical and practical aspects of selected fiber blend color formulation functions[J]. Color Research and Application, 2007,9(4):213-219.

[5] DAVIDSO H R, TAYLOR M.Prediction of the color of fiber blends[J]. Journal of the Optical Society of America, 1965,55(1):96-100.

[6] 车江宁,陈东辉,周志华.混色纤维/天然色棉配色范围探讨[J].纺织学报,2004,25(1):15-17. CHE Jiangning, CHEN Donghui, ZHOU Zhihua. Mixed color fiber/natural color cotton color range study[J]. Journal of Textile Research, 2004,1(25): 15-17.

[7] YANG Hongying, ZHU Sukang, PAN Ning. On the Kubelka-Munk single-constant/two-constant theories[J]. Textile Research Journal,2010,80(3): 263-270.

[8] 许佳艳.涤棉双组份纤维混合计算机辅助配色的研究[D].杭州:浙江理工大学,2013. XU Jiayan. The study on computer aid matching for colored fiber blends of polyester and cotton[D].Hangzhou:Zhejiang Sci-Tech University,2013.

[9] 徐锦龙.有色纤维色差的测定方法[J].合成纤维工业,1993,16(5):42-45. XU Jinlong. Measurement of colour difference of colored fiber[J].Synthetic Fiber Industry,1993,16(5):42-45.

[10] USUI S, YARI Y,NAKAUCHI S.Neural networks for device-independent digital color imaging[J]. Information Sciences, 2000,123(1):115-125.

[11] 李莉, 张秉森. 基于BP神经网络的织物染色计算机配色方法研究[J]. 系统仿真技术, 2006, 2(4):217-220. LI Li, ZHANG Bingsen. Research on color matching in textile dyeing based on BP neural network[J]. System Simulation Technology,2006,2(4):217-220.

[12] 王巍娟.基于隐层改进的BP网络在织物染色配色中的应用研究[D].青岛:青岛大学,2009:34-36. WANG Weijuan. Research on application of BP neural networks in computer color matching for textile dyeing based on hidden layer improvement[D]. Qingdao: Qingdao University, 2009:34-36.

[13] 熊峰,龙红叶,胡晓梅,等. 动量因子BP神经网络算法在设备故障预测中的应用[J].制造业自动化,2011,33(12):13-16. XIONG Feng, LONG Hongye, HU Xiaomei, et al. The application of predicting the device status using the momentum divisor ANN algorithm[J]. Manufacturing Automation,2011,33(12):13-16.

Application of colored fiber mixed models in gray spun yarn

CHENG Lu, MA Chongqi, WANG Yujuan, LIU Jianyong

(SchoolofTextiles,TianjinPolytechnicUniversity,Tianjin300387,China)

At present, most of color spinning enterprises still rely on experienced color matching persons for color matching, and some problems such as low color matching efficiency and poor accuracy still exist in the production. In order to solve these problems, back propogation(BP) neural network method was proposed to predict black and white fiber color matching in comparison with the prediction results using the Datacolor MATCH system simulation method and color mixing based model Kubelka-Munk two-constant theory. The above-mentioned three methods were all determined to be effective in predicting color mixing of black fiber and white fiber in gray spun yarns. The relative errors were controlled within 7.36%, and the color differences between formula and standard samples were less than 1. It is found that the matching method based on BP neural network shows the optimal applicability and accuracy, and the relative error is below 3.08%.

gray spun yarn; color matching method; model; Kubelka-Munk two-constant theory

10.13475/j.fzxb.20160605605

2016-06-22

2017-03-29

国家重点研发计划专题(2016YFB0302801-03)

程璐(1993—)，女，硕士生。主要研究方向为色纺纱计算机配色技术。马崇启，通信作者，E-mail:tjmcq@tjpu.edu.cn。

TS 104.5

A