基于向量自回归模型的舰船维修价格波动预警机制

杜军岗， 黄 栋， 叶卫民

(海军工程大学 装备经济管理系, 武汉 430033)

基于向量自回归模型的舰船维修价格波动预警机制

杜军岗， 黄 栋， 叶卫民

(海军工程大学 装备经济管理系, 武汉 430033)

针对舰船维修价格管理计划性较强和宏观经济环境复杂多变的矛盾，在对舰船维修价格波动预警机制分析的基础上，选取了舰船维修价格波动预警指标，设置了警限，建立了舰船维修价格波动预警指标体系。基于样本数据相关性、平稳性和协整性检验分析结果，引入非平稳时间序列建模方法，建立了舰船维修价格波动的向量自回归预警模型，借助Granger因果关系检验、脉冲响应函数分析对模型进行动态分析，并优化了预警模型。最后，基于优化模型预测舰船维修价格波动趋势，进行了预警分析。

舰船维修价格；波动预警；向量自回归模型

在市场经济条件下，舰船维修价格受社会价格水平变化影响较大。舰船维修价格指数则是反映不同时期舰船维修价格水平的变化方向、趋势和程度的经济指标，它只能反映舰船维修价格的历史变化，并不能对未来舰船维修价格的趋势进行预测分析。舰船维修保障工作既要实行严格的计划管理制度，又面临复杂多变的宏观经济环境。随着军民融合深度发展不断推进，民营修船企业参与舰船维修工作会更加频繁，舰船维修价格的市场化特征将越来越显著，届时舰船维修价格计划管理与宏观市场价格的波动性这对矛盾将更加突出。这不仅对舰船维修任务本身的安排提出更高要求，同时也对相关经费计划安排的预见性与科学性提出更高要求。因此，有必要结合舰船维修价格波动特点进行价格预警机制研究。

1 舰船维修价格波动预警机制分析

预警机制是指能灵敏、准确地昭示预警目标前兆，并能及时提供警示的机构、制度、信息、方法、举措等构成的预警系统，其作用在于超前反馈、及时布置、提高管理的效率。简单来说，预警机制就是根据警兆指标的客观数据，用预警模型的形式分析、反映出警情指标的状况。

近年来，随着舰船战技指标的大幅提高，其系统复杂性越来越强，加之社会价格水平波动频繁，使得舰船维修价格受多种因素的交错影响，但也表现出一定的变化规律性[1]。从已有研究来看，舰船维修价格波动与宏观价格水平之间存在着显著的相关性。在这种情况下，维修价格波动预警有其可行性和必要性，对提高舰船装备维修保障效益具有十分重要的意义。

舰船维修价格波动预警机制就是通过选择和建立预警指标体系，找出舰船维修价格指数和与其联系紧密的宏观价格指数的相互联系，分析并预测舰船维修价格指数变化规律，以预测舰船维修价格未来发展趋势，提升舰船维修计划的科学性和有效性。建立舰船维修价格预警机制要坚持科学性、实用性和可操作性原则，以及规范与实证分析相结合原则。

目前，关于舰船维修价格波动预警的研究很少，但其他领域中关于预警机制的研究成果对本文有很好的借鉴意义。如黄继鸿等[2]采用了景气指数法、基于概率模式分类法、判别式分析法和人工神经网络预警方法来对经济形势进行预测，并分别以预警指标的选择、针对不同的经济对象选择合适的预警方法、预警警限的动态确定论述了需要注意的问题；李莉[3]从分析影响石油价格的相关因素入手，构建了我国石油进口价格预警指标体系，建立了一套符合我国石油进口价格现状的监测预警系统，从而对石油价格的未来区间走势进行预测和报警；王道冠[4]通过对国内外房地产预警系统历史、现状的深入研究，对房地产预警系统基本方法的详细讨论，并在理论研究的基础上建立一套关于房地产预警系统的指标体系；尹贻金[5]13在研究羊毛价格预警机制时，按照明确警情、寻找警源、分析警兆、预报警度的4个步骤展开研究，采用机器学习方法，建立了羊毛价格预警模型。

从以上预警机制研究文献来看，目前进行价格波动预警的方法主要有3种：专家经验判断方法、计量经济模型方法和机器学习方法。根据建立舰船维修价格预警机制的原则，针对舰船维修价格数据的小样本特点，本文首先基于专家经验判断方法建立舰船维修价格波动预警指标体系，然后采用计量经济模型方法，建立舰船维修价格指数与预警指标体系之间的计量经济模型，以此开展舰船维修价格波动预警机制研究。

作为一种非结构化的计量经济模型，向量自回归(Vector Auto Regression,VAR)模型常用于预测相互联系的时间序列系统及分析随机扰动对变量系统的动态影响。该模型回避了结构化模型的要求，能更好地发掘时间序列变量间的影响关系，被广泛应用于实证研究中。其模型的数学表达式为[6]

Yt=A1Yt-1+A2Yt-2+…+

ApYt-p+BXt+εt

(1)

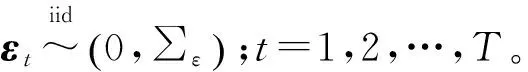
在VAR模型基础上，可进行变量间的Granger因果关系检验[7-8]及脉冲响应函数分析[9]，以对变量之间的影响关系进行动态分析。

2 舰船维修价格波动预警指标体系

2.1 预警指标变量的选取

当舰船维修价格波动发生时，维修价格指数会随之变化，因此本文选取舰船维修价格指数(Ship Maintenance Price Index, SMI)为警情指标。舰船维修价格指数指的是舰船维修的“价格变化”[10]，在选取警兆指标变量时要选择对舰船维修价格变化影响较大的因素。在舰船维修价格中，材料费和工时费占维修价格比重最大，两者合计占75%～80%。因此，选择居民消费价格指数(Consumer Price Index, CPI)、工业品出厂价格指数(Product Price Index, PPI)和职工平均货币工资指数(Staff Average Salaries Index, SASI)作为警兆指标变量[11-12]。为了简便、直观，使不同质的数据具有可比性，本文采用定基指数形式，样本区间为1994—2016年，以1994年数据为基期，如表1所示。

表1 舰船维修价格波动预警系统各指标数据

2.2 预警警限的制定

在预警警限制定的过程中，一般要遵循多数原则[5]18：它建立在对舰船维修历史长期定性分析基础之上，并假定多数年份的维修价格指数波动总体情况稳定。在表2中给出了1994—2016年舰船维修价格指数每年的变化率。

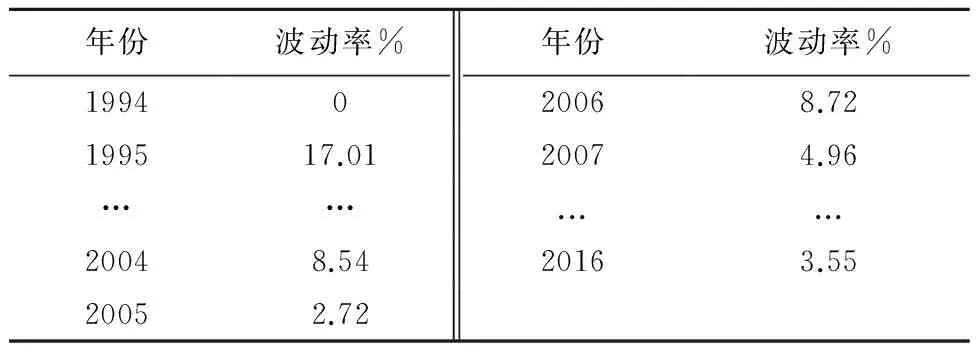
表2 舰船维修价格指数变化情况

表2中，舰船维修价格指数变化率在[0，5%)区间的有10个年份，该区间属于合理影响，为无警区间；[5%，10%)区间为轻警警限，有4个年份处于轻警区间；[10%，15%)区间为中警警限，2个年份处于中警区间内；[15%，20%)区间为重警警限，7个年份处于重警区间内；20%(含)以上为巨警警限，有1个年份处于重警区间内。其中，无警状态代表舰船维修价格运行平稳，预期价格与现行价格基本持平；轻警状态代表舰船维修价格运行基本平稳，预期价格与现行价格差异较小，可以适当进行价格调整；中警状态代表舰船维修价格运行波动较大，预期价格与现行价格差异较大，需要按照实际情况进行价格调整；重警状态代表舰船维修价格运行波动很大，预期价格与现行价格差异很大，需要进行较大的价格调整；巨警状态代表舰船维修价格运行极不稳定，预期价格与现行价格差异极大，需要进行大幅价格调整。

2.3 舰船维修价格预警机制指标体系结构

通过对警兆指标变量数据进行分析和归纳，按照指标的层次关系，构造舰船维修价格预警指标的体系结构，如图1所示。

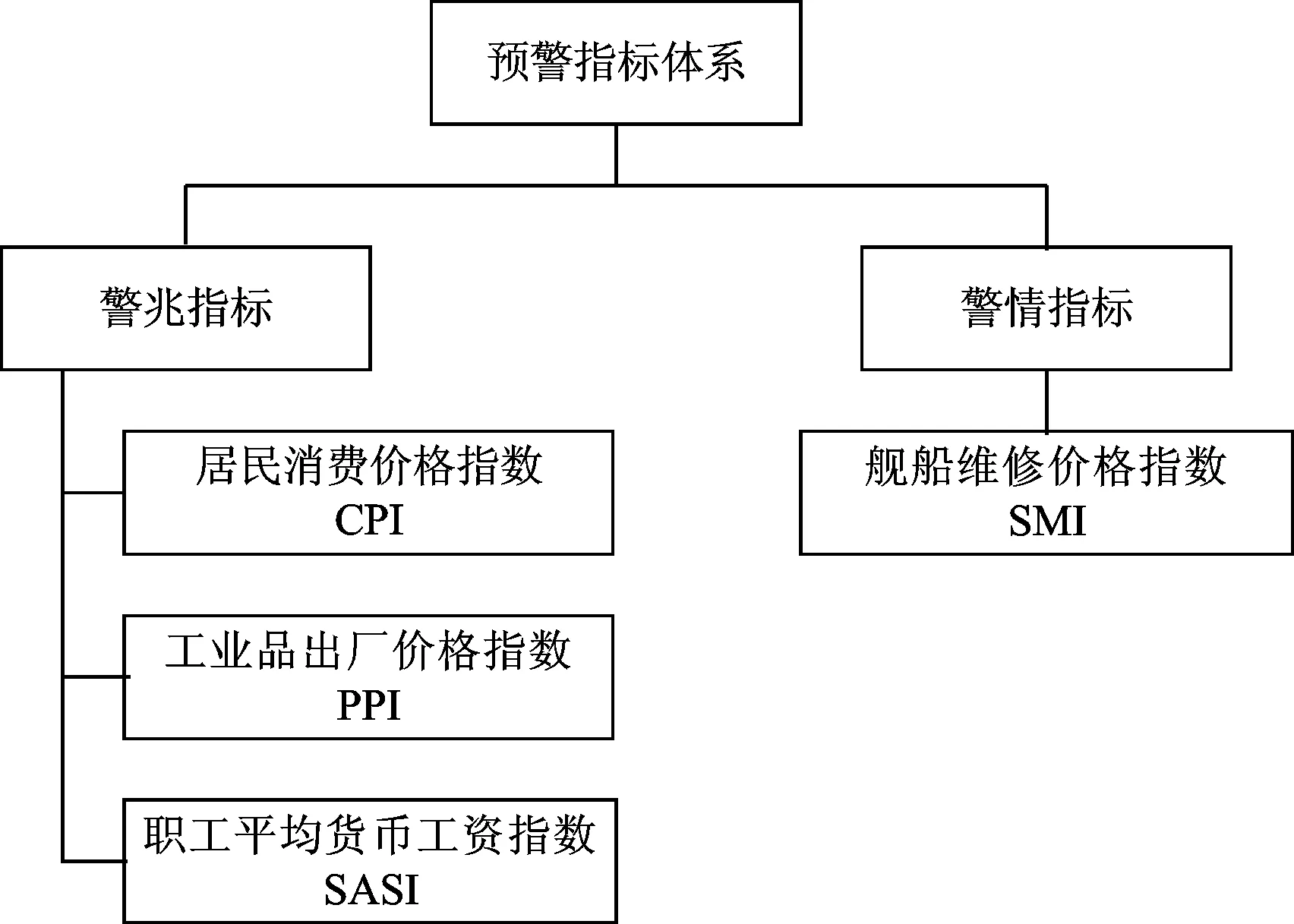
图1 价格预警指标体系

3 舰船维修价格预警模型的构建

3.1 变量相关性及数据形态检验

在预警模型构建前，本文对舰船维修价格预警指标体系中各变量(SMI、CPI、PPI和SASI)，取自然对数得到LNSMI、LNCPI、LNPPI和LNSASI作为研究对象，以免在建模过程中出现异方差现象。

3.1.1 相关性检验

本文通过计算LNSMI、LNCPI、LNPPI和LNSASI样本数据的相关系数，发现4种变量之间的相关性很强。

3.1.2 平稳性检验

为进一步确定具有较强相关性的时间序列之间的内在联系，需要进行序列之间的协整检验，以验证各时间序列变量之间是否存在长期均衡关系。如果存在，则可建立各变量间的VAR模型。

在开始检验之前，为避免伪回归现象出现，则需要进行变量的平稳性检验，这也是协整检验的前提。

本文对变量的平稳性检验采用了单位根(Augmented Dickey-Fuller test，ADF)的检验方法[13]。通过观察4种时间序列的变化趋势，本文采用含有常数项和时间趋势项的检验形式。对其差分序列，选择含有常数项而不含时间趋势项的检验形式。为保证残差值非自相关，检验过程中滞后期的选择采用赤池信息准则(Akaike’s Information Criterion，AIC)。结果表明：LNSMI、LNCPI、LNPPI和LNSASI都是I(1)的，说明这些时间序列经过一阶差分后是平稳的。

3.1.3 协整性检验

LNSMI、LNCPI、LNPPI和LNSASI属于同阶序列，通过了平稳性检验，可以进行协整性检验。本文待检验变量数为4，宜采用Johansen检验方法进行协整研究。结果表明:在95%的置信水平上，4种时间序列间存在协整关系的假设成立，存在长期均衡关系，具有共同的变化趋势。基于此，可以对4种时间序列变量建立VAR模型，研究四者的动态影响关系。

3.2 基于VAR的舰船维修价格波动预警模型及优化

本文采用协整系统主要表现形式之一的向量自回归模型(VAR)，对LNSMI、LNCPI、LNPPI和LNSASI之间关系进行建模分析。下面对VAR模型构建及其优化过程进行详细分析。

3.2.1 VAR模型的构建

1) 滞后阶数的选取。综合考虑Log Likelihood(LogL)、Likelihood Ratio(LR)、Final Prediction Error (FPE)、AIC和Hannan-Quinn(HQ)等检验标准，确定最佳滞后阶数为2。

2) 模型的建立。根据以上分析，建立滞后阶数为2的VAR模型。结果如表3所示。

表3 VAR模型各参数及方程检验结果(“C”下方横线以下为检验项)

从表3中结果来看，LNSMI方程拟合效果达到较高水平。

3.2.2 各指数对舰船维修价格指数的影响机制分析

基于前文构建的VAR模型，运用Granger因果关系检验和脉冲响应函数分析方法，分析价格指数与舰船维修价格指数间的影响关系，以及受到价格指数变化冲击时，舰船维修价格指数的动态变化规律。

1) Granger因果关系检验。以舰船维修价格指数为因变量，其他指数为自变量，对舰船维修价格指数与价格指数间Granger因果关系进行检验。检验结果表明:在取95%概率的置信水平上，LNCPI、LNPPI和LNSASI对LNSMI的综合解释能力均较显著，能够引起舰船维修价格指数波动。

2) 脉冲响应函数分析。Granger因果关系检验结果表明:LNCPI、LNPPI和LNSASI能够引起LNSMI发生变化。经分析发现，当分别给LNCPI、LNPPI和LNSASI一个冲击后，对舰船维修价格指数的影响结果略有差异。其中，LNCPI对LNSMI的影响滞后1期，LNPPI对LNSMI的影响滞后1～2期，LNSASI对LNSMI的影响滞后1～2期，之后趋于稳定。

3.2.3 舰船维修价格波动预警VAR模型的优化

综合考虑Granger因果关系检验和脉冲响应函数分析的结果，对VAR模型中LNSMI方程进行优化。结果如表4所示。

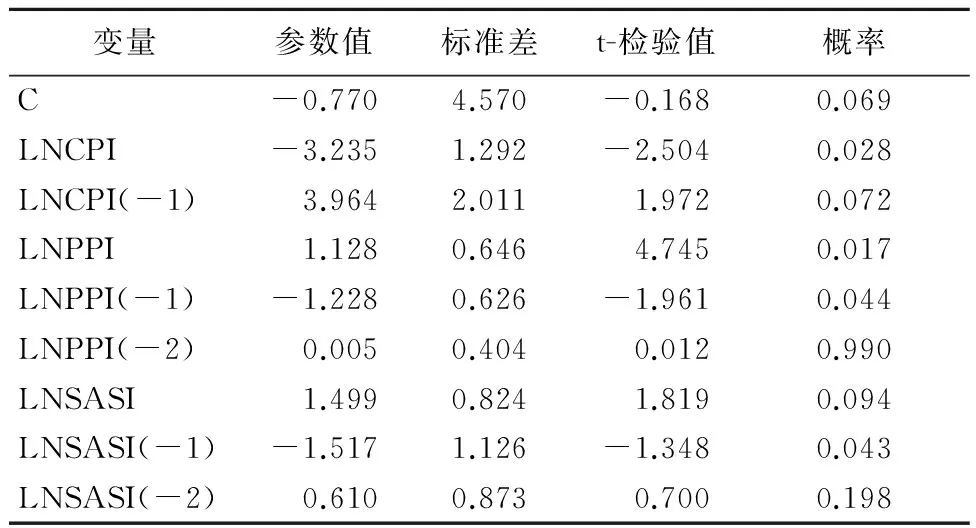
表4 LNSMI模型Eviews统计分析结果

检验结果发现，该模型的R-squared为0.990，说明拟合效果很好。根据t-检验结果，在95%的置信水平下，有6个系数是显著的，分别为C、LNCPI、LNCPI(-1)、LNPPI、LNPPI(-1)和LNSASI(-1)，对其他数据予以剔除，再次建立模型分析，以提高建模的有效性，结果如表5所示。

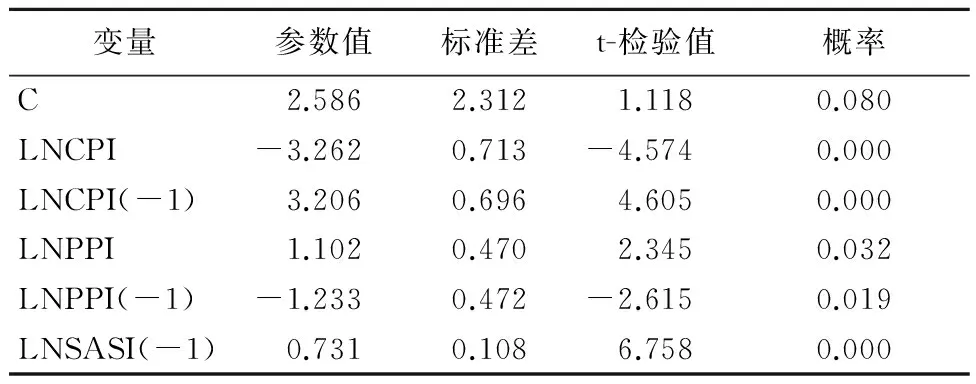
表5 优化的LNSMI模型Eviews统计分析结果

观察优化之后的模型，R-squared为0.992，拟合优度仍然处于显著水平，而且t-检验效果较之前有很大提升，置信度在95%的水平以上，建模结果可以使用。所得模型如下：

YLNSMI=2.586-3.262×XLNCPI+

3.206×XLNCPI(-1)+1.102×XLNPPI-

1.233×XLNPPI(-1)+0.731×XLNSASI(-1)

(2)

3.3 舰船维修价格波动预警应用

基于上述构建的优化模型，预测2017年舰船维修价格指数，以便更好地阐述和分析舰船维修价格指数的预测问题，并为预警系统提供数据资料，确定其所处的预警区间，得出预警结论。

在预测之前，首先需要收集数据。分析式(2)，需要的数据有2016和2017年CPI和PPI值，2016年职工平均货币工资指数值。其中，部分数据已知。由于2017年CPI和PPI未知，需要根据以前年度数据对其预测。由于2016-11至2017-02的CPI分别达到102.3、102.1、102.5和100.8，PPI分别达到103.3、105.5、106.9和107.8，已经出现上涨趋势，因此本文假设2017年CPI和PPI分别为103和106。将它转换为定基指数及自然对数形式之后与其他已知数据共同代入模型，即可预测出2017年舰船维修价格指数预测值的自然对数形式，再经过转化后就可以得出2017年舰船维修价格指数预测值。

下面为计算的具体过程：

YLNSMI(2017)=2.586-3.262×5.252+

3.206×5.222+1.102×5.238-

1.233×5.190+0.731×7.261=6.877

将以上所得自然对数形式值转化为舰船维修价格指数定基指数形式为969.713，即为2017年舰船维修价格指数预测值，转换为环比指数为119.973，其波动率达到了19.973%。

考虑多数原则条件下警限划分区间，得出2017年舰船维修价格预测值处于重警区间，预期价格波动较大，需要进行较大的价格调整。

4 结 束 语

本文基于VAR模型对舰船维修价格波动预警机制进行了研究，建立了舰船维修价格波动预警指标体系，通过1994—2016年的样本构建了预警模型并进行了相关实证检验和分析，最后利用脉冲响应函数分析结果，对舰船维修价格波动预警模型进行了优化。结果表明：CPI、PPI和职工平均货币工资指数是舰船维修价格波动的Granger原因，并且这种影响具有一定的时滞性；根据优化模型对2017年舰船维修价格波动进行预警分析，发现其波动率较大，达到了重警区间，需要对舰船维修价格进行较大调整，以防出现费用风险问题。舰船维修工作一方面有较大的计划性，另一方面面临复杂多变的宏观经济环境，必须加强对舰船维修价格波动的预警，本文方法对处理该问题提供了一种解决思路。

References)

[1]杜军岗，魏汝祥，刘宝平．基于PSO优化LS-SVM的小样本非线性协整关系检验研究[J]．系统工程理论与实践，2014，34(9)：2322-2331．

[2] 黄继鸿，雷战波，凌越．经济预警法研究综述[J]．系统工程，2003，21(3)：52-63．

[3] 李莉．我国石油进口价格风险预警机制研究[D]．南充：西南石油大学，2006：40-48．

[4] 王道冠．从政府角度研究房地产住宅价格预警体系：以赣州为例[D]．赣州：江西理工大学，2011：7-17．

[5] 尹贻金．中国羊毛价格预警机制研究[D]．吉林：吉林农业大学，2012：12-18．

[6] SIMS C A．Macroeconomics and reality[J]．Econometrica，1980(48)：41-48．

[7] ENGLE R F, GRANGER C W J. Cointegration and error correction representation[J]. Estimation and Testing Econometrica, 1987(55)：251-276．

[8] 庞皓．计量经济学[M]．北京：科学出版社，2012：329-332．

[9] 高铁梅．计量经济分析方法与建模[M]．北京：清华大学出版社，2006：249-284．

[10] 杜军岗，魏汝祥，刘宝平．技术进步对舰船维修费影响的Hedonic模型研究[J]．统计与决策，2012，28(6)：141-145．

[11] 杜军岗，魏汝祥．基于VAR的物价对舰船维修工时费率影响的动态计量分析[J]．海军工程大学学报，2012，24(2)：98-103．

[12] 杜军岗，黄栋，梁新．舰船维修Hedonic价格指数模型的构建[J]．海军工程大学学报，2016，26(5)：34-39．

[13] 李子奈，潘文卿．计量经济学[M]．北京：高等教育出版社，2005：320-336．

(编辑：李江涛)

Research on the Early Warning Mechanism upon Ship Maintenance Price Fluctuation Based on VAR Model

DU Jungang, HUANG Dong, YE Weimin

(Department of Equipment Economics and Management， Naval University of Engineering， Wuhan 430033， China)

In light of the conflict between the strong plan of ship maintenance price management and the complication of macro-economic environment, this paper establishes ship maintenance price fluctuation early warning index system after the early warning index selection and the warning limits setup, on the basis of the analysis of the ship maintenance price fluctuation early warning mechanism. The analysis result is tested based on the pertinence, stationarity and cointegration of the sample data. With the introduction of the non-stationary time series modeling, the vector autoregression(VAR)model of ship maintenance price fluctuation early warning mechanism is built, and then the Granger causality test, impulse response function analysis are used for the dynamic analysis of the VAR model. Hence, the VAR model gets optimized. Finally, the ship maintenance price fluctuation early warning model is used to predict the future ship maintenance price fluctuation, and to provide the early warning analysis.

ship maintenance price; fluctuation early warning; vector autoregression (VAR)model

2017-03-13

海军工程大学自然科学基金资助项目(HGDQNEQJJ15018)；海军工程大学科研发展基金资助项目(2016108)

杜军岗(1984—)，男，讲师，博士，主要研究方向为装备经济管理。

F270

2095-3828(2017)03-0057-05

A DOI 10.3783/j.issn.2095-3828.2017.03.010