高光谱影像的近邻加权拉普拉斯降维方法
路 易, 郭 静, 于少波
(1. 装备学院 研究生管理大队, 北京 101416; 2. 装备学院 复杂电子系统仿真实验室, 北京 101416)
高光谱影像的近邻加权拉普拉斯降维方法
路 易1, 郭 静2, 于少波1
(1. 装备学院 研究生管理大队, 北京 101416; 2. 装备学院 复杂电子系统仿真实验室, 北京 101416)
针对高光谱影像数据中存在信息冗余和非线性结构的现象,以及数据分布不均匀时拉普拉斯特征映射近邻点选择不恰当的问题,提出了一种基于Cam加权距离的拉普拉斯改进算法,用于高光谱影像数据降维以压缩数据量并提高分类精度。首先对波段分组去除奇异波段,然后用基于Cam加权距离的拉普拉斯特征映射算法对剩余数据降维,最后将结果输入最小距离分类器进行高光谱影像分类。通过Indiana Pines数据集进行验证,实验结果表明:与线性降维主成分分析法和非线性降维拉普拉斯特征映射相比,基于Cam加权距离的拉普拉斯特征映射算法分类精度更高。
Cam加权距离;拉普拉斯特征映射;非线性降维;波段选择
高光谱图像数据包括地物的二维空间信息和光谱波段信息,具有“图像立方体”的形式和结构。高光谱图像数据量大、数据冗余严重、谱间相关性强,为得到精确的分类结果,分类前对高光谱图像数据进行降维处理尤为重要。高光谱数据降维方法主要分为2类:特征选择和特征提取。高光谱图像的特征选择是波段组合优化问题,即选择出信息量较大、相关性较小、类别可分性较好的波段组合。与特征选择相比,特征提取是对原始高光谱数据进行数学变换,然后选取变换后的前n个特征作为降维之后的n个成分,实现数据降维[1]。
特征提取可以挖掘原始数据的隐含信息,可分为线性特征提取和非线性特征提取。主成分分析法(PrincipalComponentAnalysis,PCA)[2]和最大噪声分离变换(MaximumNoiseFraction,MNF)是目前应用广泛的线性特征提取方法。但实际上,在高光谱图像数据的同类地物中和类间都存在非线性特性,在光谱维上尤为明显。如果用传统的线性模型对高光谱图像进行处理无疑会丢失有用的信息。近年来,非线性流形学习方法在高光谱降维取得一定成果。常用的流形学习算法主要包括等距映射[3]、局部线性嵌入[4]、拉普拉斯特征映射(LE)[5]、局部切空间排列算法[6]等。拉普拉斯特征映射方法与线性方法PCA和非线性的其他流形学习方法相比,在低维流形保持能力、抵抗噪声能力、处理稀疏数据能力以及算法计算复杂度上都有一定的优势。但在参数选择、邻域计算、大尺度应用等方面仍需进一步研究。提出基于Cam加权距离的拉普拉斯特征映射,即在邻域计算上做出了改进。具体做法为:用Cam加权距离替代拉普拉斯特征映射构建邻域时所用的欧氏距离。
本文先通过相关系数矩阵对原始数据进行波段选择,再分别用主成分分析法、拉普拉斯特征映射和基于Cam加权距离的拉普拉斯进行降维,将降维后的结果输入最小距离分类器进行高光谱图像分类,比较各方法的总体分类精度和计算时间,实验结果表明:基于Cam加权距离的拉普拉斯可以得到更好的效果。
1 高光谱影像降维
首先对高光谱影像原始数据进行波段选择,在这一过程中用到了自动子空间划分的相关理论。自动子空间划分是高光谱影像常用到的特征选择方法。本文用此方法先去除原始数据中少量的奇异波段,然后对剩下的数据进行非线性降维。本文提出的基于Cam加权距离的拉普拉斯降维方法是在拉普拉斯特征映射算法上进行了改进。拉普拉斯特征映射是近年来应用到高光谱影像的非线性特征提取方法[7]。
1.1 自动子空间划分
自动子空间划分(Auto-SubspacePartition,ASP)方法通过定义波段相关系数矩阵及其近邻可传递相关矢量,将高光谱数据空间划分为适合的数据子空间。这种划分方法有着充分的理论依据,反映了数据的局部特性[8]。在对高光谱影像进行波段选择时,根据高光谱影像具有相邻谱段相关性强的特点,通常用此方法结合波段指数寻找最佳波段。本文提出了在特征提取前首先对原始数据所有波段进行分组,依据式(1)去除相关性极小的奇异波段,然后再进行特征提取的改进方案。
(1)

1.2 拉普拉斯特征提取方法

1) 计算像素点xi和xj的欧氏距离,构建邻域图G。当xj是xi邻域k中的点时,xi与xj之间存在边长为两者欧氏距离的无向边。
2) 计算G每条边的权重,得到权重矩阵W。两像素点间的权重系数
(2)
式中,σ2为径向基核函数的方差。如果xj不是xi邻域k中的点,则wij=0。
3) 通过极小化目标函数计算低维嵌入坐标Y。目标函数为
E(Y)=∑ij(yi-yj)2wij
(3)

4∑ijyiyjwij=2yTLy
(4)
为求得唯一流形坐标,附加条件yTDy=1,于是
Ly=λDy
(5)
降维后的数据为除0外的d个特征值对应的特征向量。
2 基于Cam加权距离的拉普拉斯降维
当起始的样本数量较少或样本数据不是标准正态分布时,基于欧氏距离来选取邻域的方法并不能很好地构建邻域信息。目前已有实验证明高光谱数据空间存在非高斯分布结构[9],并且在高光谱影像空间中,每类样本数据量多少不一。因此,在高光谱影像处理中直接应用基于欧氏距离的传统k近邻方法效果不佳。 传统k近邻方法选择最近的k个样本,可能出现信息的冗余以及重要信息的丢失,如图1所示。实线区域内为k近邻方法选择的点,对于不均匀的分布k近邻选择的点都集中在一侧,导致信息冗余且另一侧信息丢失,因此这些近邻点不能很好地重构中心点。为此,本文用基于Cam加权距离的拉普拉斯方法对高光谱数据进行降维,该方法可更合理地构造出样本点的邻接信息,使得高光谱数据的低维流形更准确的表达原始高维信息。
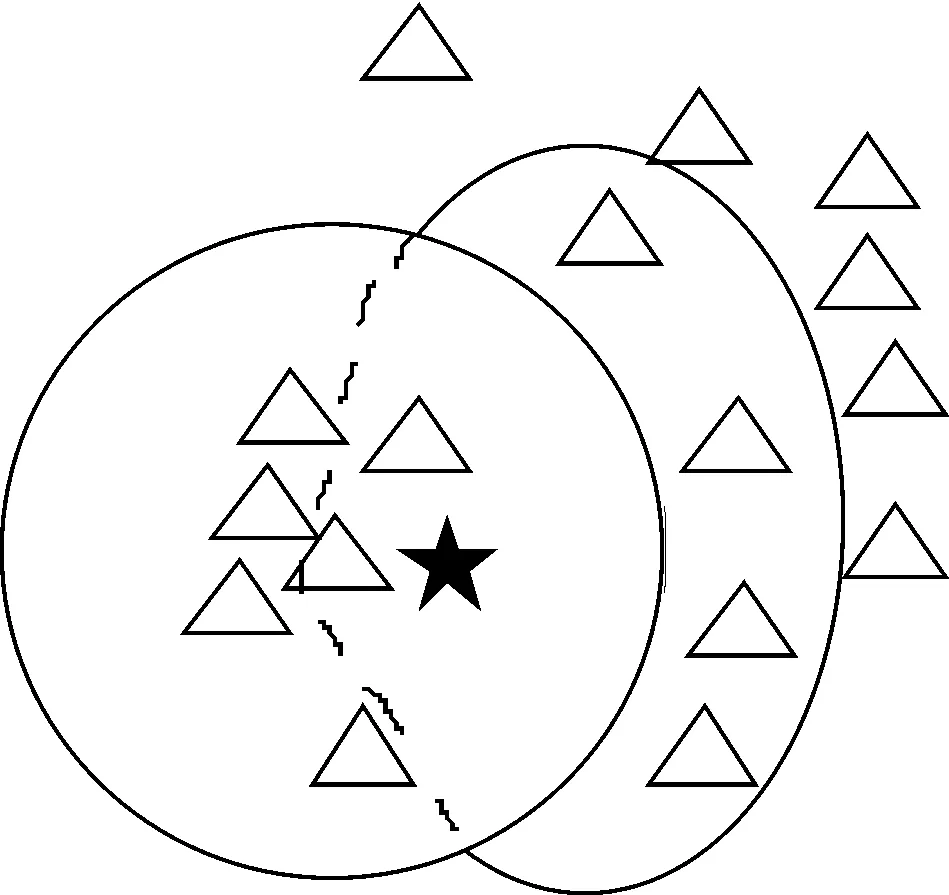
图1 欧氏距离(实线)和加权距离(虚线)
2.1Cam分布
随机向量X定义为
(6)
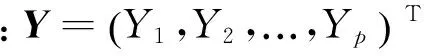
2.2 加权距离
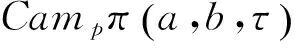

(7)
式中,a,b,τ为待估计参数。
2.3 参数估计
Y服从标准正态分布,其概率密度函数为
(8)

(9)
那么
E(X)=c1bτ
(10)
E(‖X‖)=c2a
(11)
式中,c1,c2为常量。
(12)
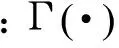
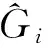
(13)
(14)
于是得到
(15)
将以上计算的Cam加权距离替代拉普拉斯特征提取中的欧式距离,可以解决数据分布不均的问题,从而更好地对高光谱数据降维。
2.4 本文降维方法步骤
本文提出的高光谱影像数据降维方法将特征选择和特征提取结合,流程如图2所示。具体方法步骤为:
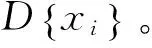
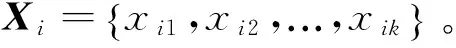
7) 由式(3)~式(5)计算低维嵌入坐标Y。
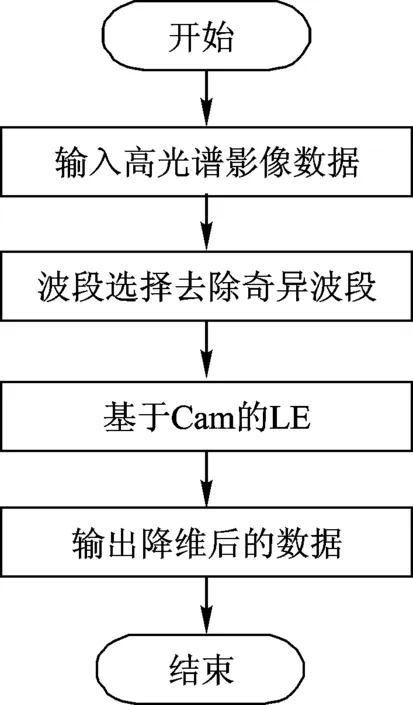
图2 本文降维方法流程
3 实 验
3.1 实验数据
实验数据集为由成像光谱仪AVIRIS获取的美国印第安纳州某农林混合实验场(IndianaPines)高光谱图像。波长范围为0.4 ~ 2.5μm,空间分辨率为25m,空间大小为145×145个像素点,从原始220个波段中去除水汽吸收波段和低信噪比波段([104~108],[150~163],220)后,保留了其中200个波段进行数据处理。数据集中共有16类地物。IndianaPines单一波段图如图3所示。

图3 Indiana Pines单一波段图
3.2 实验结果
对有200个波段的IndianaPines数据进行波段选择,计算相关系数矩阵。去除相关系数小于0.2的波段,剩余184个波段。首先对有184个波段的高光谱图像用最小距离法进行分类,总体分类精度(OverallAccuracy,OA)为84.99%,比直接用200个波段进行分类提高1.1%。说明此时有效去除了16个奇异波段。接着对含有184个波段的高光谱数据进行实验,分为用PCA、LE和基于Cam权重的LE进行降维,将降维后的结果输入最小距离分类器比较实验结果。
图4为PCA、LE和Cam-LE分别将184个波段的高光谱数据降到不同维数下的总体分类精度条形图。表1为对IndianaPines图像分类的运行时间和总体分类精度对照表。表1的第一行为对原始数据200个波段进行分类的总体分类精度与运行时间。其余的是对波段选择后的184个波段继续进行降维并分类的总体分类精度和运行时间。图、表显示的结果均为各方法参数调到分类结果最优情况下的实验结果。
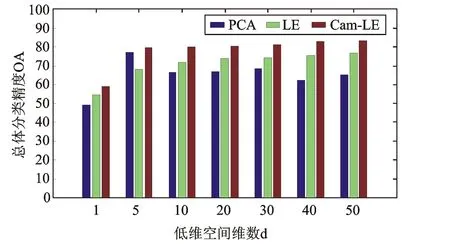
图4 PCA、LE和Cam-LE不同维数下的总体分类精度OA
实验结果显示:用PCA降到5维时,总体分类精度最高;且全过程的运行时间为9.11s,与流形学习方法相比时间最少。但在无先验知识的情况下不能直接选择出最佳维数。本文用LE进行降维时,近邻k选为9分类精度最高。用不加改进的拉普拉斯方法降维,只在降到5维时分类精度低于PCA降维后的精度,在其他维数下分类精度整体高于PCA降维后的分类精度,且随着维数增加精度呈上升趋势。LE在计算时间上高于PCA,计算时间与近邻数k有关。当k一定时,随着维数增加计算时间也逐渐增加。用基于Cam加权距离的拉普拉斯降维选取k为12时分类精度最高,分类效果较好。但因为基于图构建近邻并且需要在k近邻基础上调整近邻点,所以计算时间最长。

表1 不同维数下总体分类精度和运行时间
图5为分别用PCA、LE和Cam-LE降维后维数不超过50时,分类精度最高的分类图像。图5a)、图5c)、图5e)为理想分类结果,图5b)、图5d)、图5f)为实验分类结果,每次实验均随机分配颜色进行分类。图5a)和图5b)为用PCA降到5维时进行分类的分类图像,总体分类精度为77.34%。图5c)和图5d)为用LE降到50维时进行分类的分类图像,选取k为9,此时总体分类精度为76.65%。图5e)和图5f)为用Cam-LE降到50维时进行分类的分类图像,选取k为12,此时总体分类精度为83.54%。由图像可以明显看出第三组,即用改进后的拉普拉斯降维然后进行分类的效果最好。

a) 理想分类结果 b) PCA分类
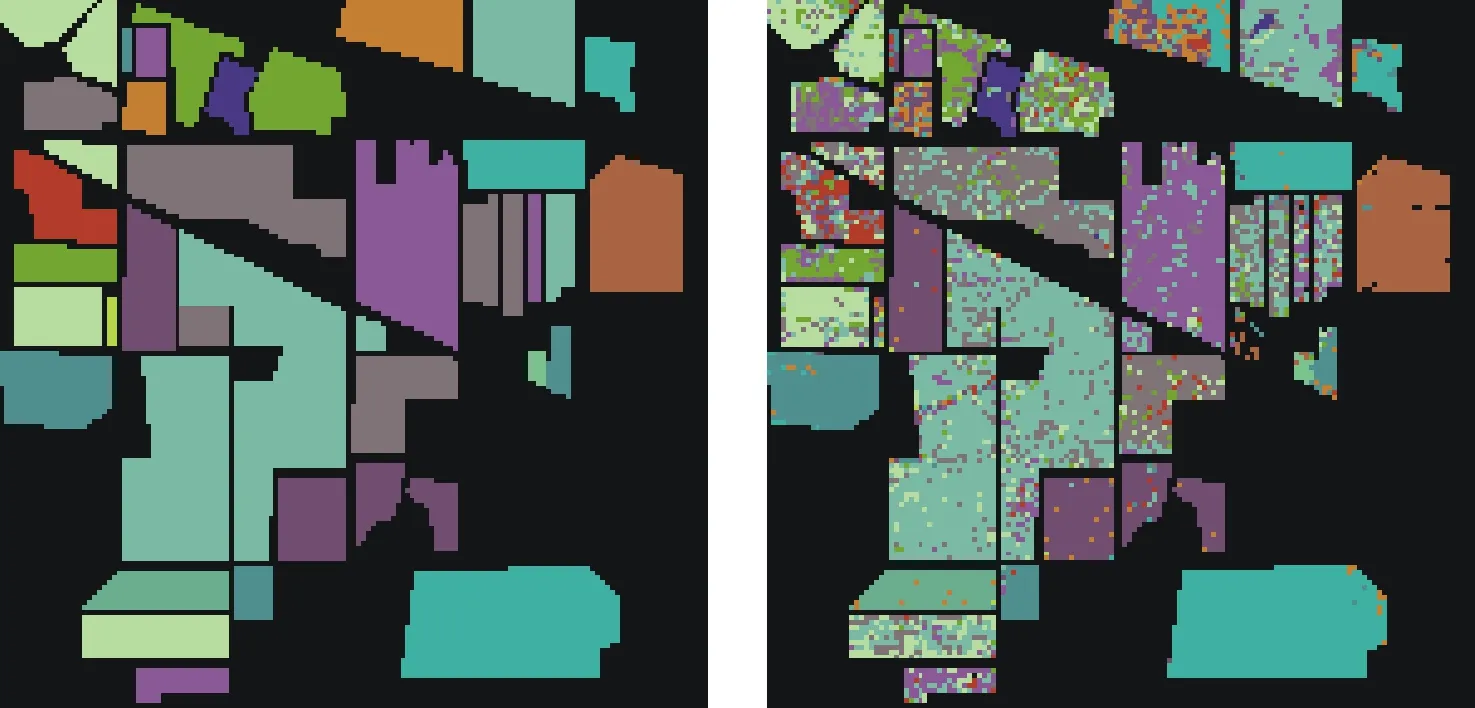
c) 理想分类结果 d) LE分类
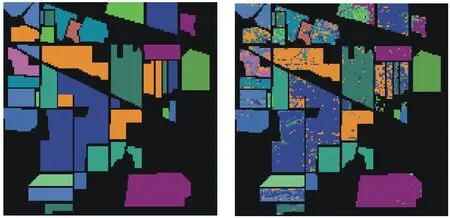
e) 理想分类结果 f) Cam-LE分类 图5 PCA、LE、Cam-LE分类图
4 结 束 语
本文提出基于Cam加权距离的拉普拉斯高光谱图像降维方法,结合最小距离分类器用IndianaPines数据集进行分类实验,并与传统的线性降维PCA和非线性流形学习降维LE算法比较。结果证明:先进行波段选择可以去除奇异波段,提高分类精度;基于Cam加权距离的拉普拉斯降维在分类精度上优于传统线性PCA和非线性的流形学习降维LE;在计算时间上基于Cam加权距离的拉普拉斯与PCA和LE相比存在劣势,但与不降维直接进行分类相比,在分类精度基本持平的情况下,计算时间更少。在本文方法基础上,加入高光谱空间信息或利用各类标签进行半监督拉普拉斯改进是下一步研究的方向。
)
[1]张兵.高光谱图像处理与信息提取前沿[J].遥感学报,2016,20(5):1062-1090.
[2]JIA X,RICHARDS J A.Segmented principal components transformation for efficient hyperspectral remote sensing image display and classification[J].IEEE Trans.Geoscience and Remote Sensing,1999,37(1):538-542.
[3]杜培军,王小美,谭琨,等.利用流形学习进行高光谱遥感影像的降维与特征提取[J].武汉大学学报(信息科学版),2011,36(2):148-152.
[4]刘嘉敏,罗甫林,黄鸿,等.应用相关近邻局部线性嵌入算法的高光谱遥感影像分类[J].光学精密工程,2014,22(6):1668-1676.
[5]孙伟伟,刘春,李巍岳.联合改进拉普拉斯特征映射和k-近邻分类器的高光谱影像分类[J].武汉大学学报(信息科学版),2015,40(9):1151-1156.
[6]SUN W,HALEVY A,BENEDETTO J J,et al.Nonlinear dimensionality reduction via the ENH-LTSA method for hyperspectral image classification[J].Selected Topics in Applied Earth Observations & Remote Sensing IEEE Journal of,2014,7(2):375-388.
[7]钱进,邓喀中,范洪冬.基于拉普拉斯特征映射高光谱遥感影像降维及其分类[J].遥感信息,2012,27(5):3-7.
[8]苏红军,杜培军,盛业华.高光谱影像波段选择算法研究[J].计算机应用研究,2008,25(4):1093-1096.
[9]路威.面向目标探测的高光谱影像特征提取与分类技术研究[D].郑州:中国人民解放军信息工程大学,2005:7.
[10]ZHOU C Y,CHEN Y Q.Improving nearest neighbor classification with cam weighted distance[J].Pattern Recognition,2006,39(4):635-645.
(编辑:李江涛)
Dimensionality Reduction for Hyperspectral Images Based on Cam Weighted Distance Laplacian Eigenmap
LU Yi1, GUO Jing2, YU Shaobo1
(1. Department of Graduate Management, Equipment Academy, Beijing 101416, China; 2. Science and Technology on Complex Electronic System Simulation Laboratory, Equipment Academy, Beijing 101416, China)
In consideration of the information redundancy and intrinsic nonlinearities, and the irrelevancy of Laplacian Eigenmap k-nearest neighbor selected for the uneven distribution of hyperspectral image data, this paper presents an improved LE algorithm based on Cam weighted distance for hyperspectral image dimensionality reduction to compact feature representation and improve the accuracy of classification. First, the band is grouped for the removal of singular band, then the Cam weighted distance Laplacian Eigenmap is used to reduce the remaining data dimension, and finally, the results are put into the minimum distance classifier for hyperspectral image classification. By verification with the Indiana Pines data set, the experimental results show that compared with linear dimensionality reduction method of PCA and nonlinear method of LE, Cam weighted distance Laplacian Eigenmap algorithm gets higher classification accuracy.
Cam weighted distance; Laplacian eigenmap (LE); nonlinear dimensionality reduction; band selection
2017-04-17
部委级资助项目
路 易(1992—),女,硕士研究生,主要研究方向为高光谱遥感。luyi9246@163.com
TP701
2095-3828(2017)03-0027-05
A DOI 10.3783/j.issn.2095-3828.2017.03.005

