基于深度神经网络的高光谱遥感影像分类方法研究

朱 江， 胡华全， 范雯琦

(1. 装备学院 研究生管理大队, 北京 101416； 2. 装备学院 复杂电子系统仿真实验室, 北京 101416； 3. 北京跟踪与通信技术研究所, 北京 100094)

基于深度神经网络的高光谱遥感影像分类方法研究

朱 江1， 胡华全2， 范雯琦3

(1. 装备学院 研究生管理大队, 北京 101416； 2. 装备学院 复杂电子系统仿真实验室, 北京 101416； 3. 北京跟踪与通信技术研究所, 北京 100094)

分类是高光谱遥感影像处理中最为重要的一部分。针对现有影像分类方法存在预处理复杂、高维特征提取困难、分类不够精确等缺陷，提出一种基于深度神经网络的高光谱遥感影像分类算法。算法首先采用最大噪声分数来降低特征空间维度，然后将自动编码器与softmax多项逻辑回归分类器组合成含有多隐藏层的神经网络，对高光谱遥感影像进行非监督型深度特征提取与分类。实验结果表明：与传统的基于线性支持向量机分类方法相比，本算法可提取更高级的表达特征，并在较短的处理时间内实现较好的影像分类精度。

高光谱遥感；影像分类；深层神经网络；自动编码器；最大噪声分数

高光谱遥感是通过光谱成像仪(imaging spectrometer)将光谱信息引入遥感成像中去的多维度空间-光谱信息感知技术[1]。由于低空间分辨率导致混合像元现象、波段间高相似性导致Hughes现象、端元与光谱不对应导致数据结构高度非线性等原因，使得高光谱影像分类一直都是具有挑战性的热点问题，众多科研人员设计了多种不同类型的分类方法[2]。文献[3]将分类器根据设计方法异同划分为：监督类方法、非监督类方法、半监督类方法、混合类方法、集成类方法和多分类器融合方法6类。文献[4]根据参与分类过程的特征类型及其描述不同，将分类器方法划分为：光谱域特征分类、空间-光谱特征分类及多特征混合分类算法3类。本文则基于高光谱影像的统计特性，根据是否引入有标签训练样本将分类器简单划分为监督类方法、半监督类方法和非监督类方法。

顾名思义，监督型分类方法通过训练具有明确标识的像元来获得最优模型，再利用该模型将全部像元映射到对应输出，并对其结果进行简单判断从而达到分类目的，主要方法包括：基于支持向量机(Support Vector Machine,SVM)的分类[5]、基于核方法的分类[6]、基于统计模型的最大似然分类[7]和基于稀疏表示的分类[8]。半监督型分类方法利用少量已标记像元和大量未标记像元训练样本来构建有效的分类器，从而降低高光谱遥感影像分类中“不适定”问题的影响。其主要方法包括：自训练分类[9]、合作训练分类[10]、基于生成模型分类[11]、基于低密度分离分类[12]和基于图的分类[13]等。相较于前2类方法，非监督型分类方法不需要任何标签样本或先验知识，易于处理与实现，常见方法包括K均值聚类[14]和NLTV(Nonlocal Total Variation)法[15]。

深度神经网络通过构建多隐藏层的神经元联结从而提取目标高维数据的深度特征，自2006年Hinton提出后被广泛用于分类当中[16]。对深度神经网络的训练可分为前段所述的监督型和非监督型。但当深度神经网络通过监督型方式进行训练时会面临以下问题：(1) 实际中标签数据稀缺，难以方便获得；(2) 求解高度非凸优化问题时会存在大量局部极值；(3) 使用梯度下降法时会发生弥散问题。因此，本文提出一种基于非监督型多隐藏层的自动编码器深度神经网络算法：首先，通过最大噪声分数(Maximum Noise Fraction，MNF)降低频谱波段数量，去除冗余相似信息；然后，采用不需要标签样本的多隐藏层自动编码器对影像进行深度特征提取，并在训练完成后使用误差反向传播(error Back Propagation，BP)方法进行参数微调以避免局部极值；最后，借助softmax逻辑回归分类器完成影像分类。

1 MNF方法和自动编码器基本原理

1.1 MNF方法

高光谱遥感成像可以同时收集地物的二维空间信息和一维光谱信息，进而生成高光谱分辨率全波段连续的遥感影像。较高光谱分辨率的最大好处就是根据光谱信息可以更加精确的对地物进行分类识别。如图1所示，不同波段下的高光谱影像组合成一个数据立方体，每一幅影像中像元记录的信息是其对应瞬时视场(Instantaneous Field of View，IFOV)内地物的辐射信息，每个像元在不同波段中的辐射信息组成了一个连续光谱曲线。然而，由于在狭窄带宽中存在数百个频带，且相邻频带之间具有高相关性，导致了信息冗余与高维数据处理困难等问题，还会产生Hughes现象。因此在分类之前需要对高光谱影像进行降维预处理，即对高维度影像信息用低维度数据来简化表征，在降低数据量的同时优化地物的特征提取。

图1 高光谱遥感成像示意图

MNF变换是一种简便高效的高光谱影像降维方法，基本原理是通过正交线性变换将所有波段的数据投影到新的特征空间中使彼此互不相关，并按照各影像质量由大到小排列各成分，这里影像质量的衡量标准是信噪比(Signal to Noise Ratios，SNR)

(1)

式中：ai为变换矩阵中的第i个变换分量；N为噪声矩阵；Y=S+N为影像矩阵，S为信号矩阵；ΓN为噪声N的协方差矩阵；ΓY为影像Y的协方差矩阵。如果对ai标准化，则式(1)可转换成如下最优化问题

(2)

通过转换后就可以利用Lagrange乘数法来求解上式。

相比较于基于信息量排列的主成分分析(PrincipalComponentsAnalysis，PCA)降维方法，MNF变换可以有效克服当影像噪声分布不均衡或噪声协方差大于信号协方差时，基于信息量排列的PCA方法可能出现的、影像质量随着主成分的增大而增大的情况。

1.2 自动编码器

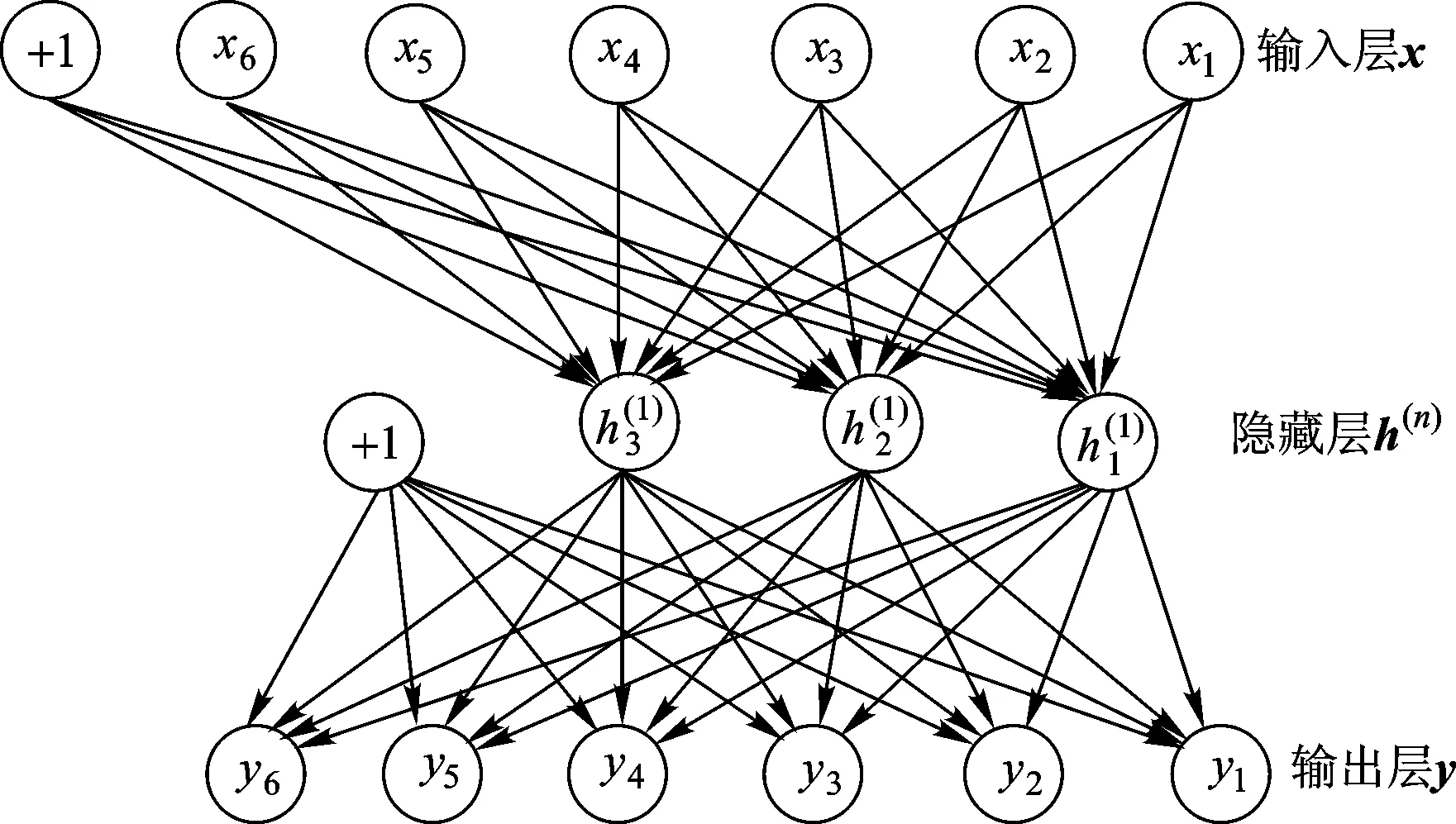
图2 自动编码器的基本结构

由图2可知，自动编码器通过对输入的数据进行非线性变换，最终使得x≈y。图2中自动编码器的基本结构在数学上可以表示为

(3)

(4)

(5)

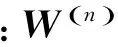
(6)

(7)

(8)

式中，∂为学习速率，设置它的主要目的是避免目标函数陷入局部极小。

2 算法设计

首先，根据式(2)使用MNF方法对高光谱影像数据进行预处理，在降低原始影像频谱波段数量的同时保留主要数据的特征信息。接下来，构建自动编码器。为了降低所设计的深度神经网络的复杂性，减少需要训练的网络参数，令编码器的每一层都具有相同的权重

W(1)=W(2)=…=W(n)=W

(9)

为了提升神经网络的学习能力，达到“深度”学习的目的，增加隐藏层层数显然要比直接增加隐藏层神经元数量更加有效。因此，在本算法中设计了含有多隐藏层的神经网络模型对影像特征进行提取与分类，即每次训练一层的隐藏节点，训练时将前一隐藏层的输出作为本层的输入，而本隐藏层的输出则作为后一层的输入。隐藏层层数根据实际影像数据来决定，这里先令n=1，根据式(3)～式(5)可得到h(1)和y的表达式

(10)

(11)

(12)

接下来，定义交叉熵代价函数

(13)

式中，m为被选取数据大小。则式中的损失函数可以表达成

(14)

式中，s为输入数据的大小。

为了简化式(10)和式(11)，将其重新写成

(15)

(16)

(17)

(18)

(19)

(20)

(21)

将上式全部代入到式(7)和式(8)中，可以得到

(22)

(23)

(24)

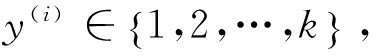
softmax(x) =P(y(i)=l|x,W,b) =

e(Wx+bl )∑je(Wx + bj )

(25)

最后用BP方法对softmax进行微调，直到模型的预测结果达到一个预期的准确率。整个算法设计可以概括为“预训练+微调”的结构，先对每一层的各参数进行预训练获得本层的局部较优解，然后再将这些局部较优的结果综合起来进行微调，进而寻求整个网络的最优设置。具体算法的设计步骤如下：

步骤1 根据式(2)对原始数据进行MNF变换，降低冗余波段数量。

步骤4 根据式(25)对softmax多项逻辑回归分类器进行训练，得到预分类结果。

步骤5 使用BP方法对深度神经网络模型进行微调，更新模型参数。重复步骤3和步骤4，直到网络模型的配置达到最优。

3 实验结果

a) 理想的地物分类结果 b) 基于线性SVM方法的地物分类结果 c) 基于本算法的地物分类结果图5 Indian Pines影像数据分类结果

3.1 实验测试集

为了验证本文算法的有效性，实验选取了国际上广泛使用的标准高光谱测试集Indian Pines和测试集Italy Pavia。其中，Indian Pines测试集为1992年6月由机载AVIRIS光谱成像仪在美国印第安纳州西北部地区的印第安松树林上空拍摄，影像大小为145 × 145像素，几何空间分辨率为20 m。在波长为0.4～2.5 μm的范围内有220个波段，本次实验去除了其中的20个包含强噪声和水汽吸收的波段，即104～108、150～163和220波段。该测试集共包括草地、作物和建筑在内的16种地物。其中，第170波段的真实影像如图3所示。

图3 Indian Pines第170波段真实影像数据

Italy Pavia测试集为帕维亚大学使用ROSIS光谱成像仪，在帕维亚市的西北方位上空拍摄的。影像大小为610 × 610像素，几何空间分辨率为20 m。在波长为0.43～0.86 μm的范围内有115个波段，本次实验去除了其中的12个包含强噪声和水汽吸收的波段。该测试集共包括公路、树木和屋顶在内的9种地物。其中，第13波段的真实影像如图4所示。

图4 Indian Pines第170波段的真实影像数据

3.2 实验结果与分析

目前，在高光谱影像分类算法中应用最为广泛的是基于SVM的机器学习方法，该方法原理简单且特别是在高维模式识别中性能优秀[18]。因此，这里采用基于线性SVM的分类方法与本文算法进行对比。此外，实验所用的计算机硬件环境为Intel Core i7-4600U，CPU 2.69G，显卡Intel(R) HD，软件环境为Windows10(64bit)，编程软件MATLAB 2014b。

由于整个测试集中的像素数量庞大，因此这里随机选取了20%的样本用于训练，剩余80%的数据用于测试。深度神经网络中层数和神经元数目的选取根据具体测试集来确定，针对Indian Pines测试集，如算法设计中所述设置深度神经网包含1个输入层，2个隐藏层和1个输出层。选取各层神经元个数分别为180、120、120、16。设置学习速率∂=0.05，预训练80次，微调200次。最终分类结果如图5所示。针对ItalyPavia测试集，如算法设计中所述设置深度神经网包含1个输入层，4个隐藏层和1个输出层。选取各层神经元个数分别为90、70、70、70、70、9。设置学习速率∂=0.05，预训练80次，微调200次。最终分类结果如图6所示。

对上述2个测试集经过重复10次实验后本算法的平均分类准确度分别为90.54%和88.44%，线性SVM的平均分类准确度分别为79.22%和76.61%。此外，线性SVM方法处理数据平均花费时间分别为32.5s和40.5s，而本算法处理数据平均所用时间仅分别为15.2s和17.2s。但是，可以看出本算法在2种地物的交界处还存在较多分类错误的问题。综上可知，在高光谱影像分类技术中引入深层神经网络模型可以有效提高地物分类精度。

a) 理想的地物分类结果 b) 基于线性SVM方法的地物分类结果 c) 基于本算法的地物分类结果图6 Italy Pavia影像数据分类结果

4 结 束 语

本文针对现有高光谱影像分类方法存在的不足，提出一种基于深度神经网络的高光谱遥感影像空谱联合分类算法。该算法具有以下优点：(1) 在预处理中引入MNF方法降低原始数据的波段维数，提高了计算处理速度；(2) 构建自动编码器与softmax逻辑回归分类器组合成多隐藏层神经网络，可以更好地进行特征深度提取与地物精准分类。实验结果表明：本算法在对高光谱影像处理中，无论是地物分类精度还是时间消耗上均优于传统SVM分类方法，证明了算法的有效性和优越性。

下一步将尝试对其他特征更复杂的影像进行分类从而验证算法的普适性，针对大规模的高光谱遥感影像进行切割分块处理。此外，还准备将本算法与其他分类方法相结合，组合成一个多分类器系统，从而达到比单一分类器更好的分类精度。

)

[1]PRASAD S,CHANUSSOT J,FOWLER J E,et al.Introduction to the issue on advances in hyperspectral data processing and analysis[J].IEEE Journal of Selected Topics in Signal Processing,2015,9(6):961-963.

[2]PLAZA A,BIOUCAS-DIAS J M,SIMIC A,et al.Foreword to the special issue on hyperspectral image and signal processing[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2012,5(2):347-353.

[3]CHUTIA D,BHATTACHARYYA D K,SARMA K,et al.Hyperspectral remote sensing classifications:a perspective survey[J].Transactions in GIS,2015,20(4):463-490.

[4]张兵.高光谱图像处理与信息提取前沿[J].遥感学报,2016(5):1062-1090.

[5]MELGANI F,BRUZZONE L.Classification of hyperspectral remote sensing images with support vector machines[J].IEEE Transactions on geoscience and remote sensing,2004,42(8):1778-1790.

[6]BUI D T,TUAN T A,KLEMPE H,et al.Spatial prediction models for shallow landslide hazards:a comparative assessment of the efficacy of support vector machines,artificial neural networks,kernel logistic regression,and logistic model tree[J].Landslides,2016,13(2):361-378.

[7]RICHARDS J A.Remote sensing digital image analysis:an introduction[M].Berlin:Springer,2013： 47-50.

[8]WRIGHT J,MA Y,MAIRAL J,et al.Sparse representation for computer vision and pattern recognition[J].Proceedings of the IEEE,2010,98(6):1031-1044.

[10]ZHANG H,LI J,HUANG Y,et al.A nonlocal weighted joint sparse representation classification method for hyperspectral imagery[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2014,7(6):2056-2065.

[11]JACKSON Q,LANDGREBE D A.Adaptive Bayesian contextual classification based on Markov random fields[J].IEEE Transactions on Geoscience and Remote Sensing,2002,40(11):2454-2463.

[12]CHI M,BRUZZONE L.Semisupervised classification of hyperspectral images by SVMs optimized in the primal[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(6):1870-1880.

[13]CAMPS-VALLS G,MARSHEVA T V B,ZHOU D.Semi-supervised graph-based hyperspectral image classification[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(10):3044-3054.

[14]JAIN A K.Data clustering:50 years beyond K-means[J].Pattern Recognition Letters,2010,31(8):651-666.

[15]ZHU W,CHAYES V,TIARD A,et al.Unsupervised classification in hyperspectral imagery with nonlocal total variation and primal-dual hybrid gradient algorithm[J].IEEE Transactions on Geoscience & Remote Sensing,2017,55(5):1-13.

[16]HINTON G E,SALAKHUTDINOV R.Reducing the dimensionality of data with neural networks[J].Science,2006,313(5786):504-507.

[17]CHEN Y,LIN Z,ZHAO X,et al.Deep learning-based classification of hyperspectral data[J].IEEE Journal of Selected topics in applied earth observations and remote sensing,2014,7(6):2094-2107.

[18]WU Y,YANG X,PLAZA A,et al.Approximate computing of remotely sensed data:SVM hyperspectral image classification as a case study[J].IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing,2016,9(12):5806-5818.

(编辑：李江涛)

Research on Hyperspectral Remote Sensing Image Classification Based on Deep Neural Networks

ZHU Jiang1， HU Huaquan2， FAN Wenqi3

(1.Department of Graduate Management,Equipment Academy,Beijing 101416,China； 2.Science and Technology on Complex Electronic System Simulation Laboratory,Equipment Academy,Beijing 101416,China； 3.Beijing Institute of Tracking and Telecommunications Technology,Beijing 100094,China)

Classification is the most important part of hyperspectral remote sensing image processing. With view to the setbacks of complex preprocessing, difficult extraction of high-dimensional features and not accurate classification existing in the current classification method, the paper raises an algorithm of hyperspectral remote sensing image classification based on deep neural networks. This algorithm first uses the maximum noise fraction to reduce the feature space dimension, then combines the auto-encoders and the multinomial logistic regression classifier sofemax into a neural networks with multiple hidden layers, to extract and classify the unsupervised deep features of hyperspectral remote sensing images. Experiments show that, in comparison with the traditional linear support vector machine (SVM) classification method, it can extract more advanced expression features and realize better image classification accuracy in a shorter processing time.

hyperspectral remote sensing; image classification; deep neural network; auto-encoder; maximum noise fraction

2017-04-17

部委级资助项目

朱 江(1990—)，男，博士研究生，主要研究方向为高光谱影像处理。nudt1990@gmail.com

TP701

2095-3828(2017)03-0014-07

A DOI 10.3783/j.issn.2095-3828.2017.03.003