实施初中数学课堂有效教学“五法”
邓汉才
【摘要】 实施有效的课堂教学,是教育教学的核心,是提高教育质量和教学效率的关键。本文从依据学生个性差异制定目标、塑原知识产生过程实现内化、以思维节点激发兴趣、合理分组进行有效交流、一题多变培养创新能力这五个方法来探讨如何实施有效课堂教学,使学生整体素质提高和个性特长得到发挥,增创班级学习的有效性。
【关键词】 目标 内化 兴趣 交流 能力
【中图分类号】 G633.6 【文献标识码】 A 【文章编号】 1992-7711(2017)05-050-01
0
课堂教学,是学生在教师的组织、指导和帮助下,承载人类知识财富,开发知能,完善人格,提高综合素质的主渠道。教师是导演,学生是演员。有效教学是指通过一段时间的符合一定教学规律的教学活动后,学生获得了预期的进步和发展,实现了教学目标和促进学生内在的发展与全面发展。
一、依据学生个性差异制定目标
根据学生个性差异而制定教学目标,突显分层教育,是素质教育的要求。素质教育,就是差异教育。学生是发展中的人,是在差异中发展的人。我们教师的责任在于发现学生的差异,尊重学生的差异,并在差异的基础上发展学生。
现代学习理论指出,促进学生学习和发展才是有效教学的根本目的,也是衡量教学活动的有效性的唯一标准。由于“每一个孩子都有一个独特的,独一无二的世界”每个学生存在着身体、个性、基础、智能等方面的差异。因此,制订教学目标时,既要有整体性,使学生和谐,全面发展,又要让不同学习层次的学生得到不同的发展;在教学中,对不同差异的学生,設置不同的教学目标来组织教学。
二、塑原知识产生过程实现内化
知识是他人实践的结果,是人类的结晶。数学课堂教学不仅要让学生学习知识和经验,而且更要以学生发展为本,倡导学生主动参与、乐于研究、勤于动手,让学生认识和体验人类创造知识的过程,将他人的结果转化为自己亲身实践的体验,把他人的经验和智慧,通过自身的感悟和践行,转化为自己的资源和精神能量。这样,才能够在教学中实现知识对学生而言的由“外”向“内”的真正转化。
三、以思维节点激发兴趣
兴趣是最好的老师。瑞士教育家皮亚杰说:“所有智力的工作都要依赖于兴趣 ”。学习兴趣是学生学习的根本动力和内驱力,学生对所学知识一旦产生兴趣,就会产生一种对知识的好奇与渴望,就想探究其中的奥妙,就会自发地去学习。激发学生的学习兴趣是使学生更好地掌握所学知识的重要途径,也是提高课堂教学效率的重要手段之一。
数学是人类思维的体操,数学活动的本质是学生数学思维活动。人们学习数学是从日常生活经验开始的,并在生活中渐渐养成了生活思维的习惯性。学生在学习数学时,需要养成数学思维习惯的时候,还保留着生活的思维。课堂教学中,要密切注意学生思维活动,吸引学生学习的注意力,启迪学生展开思维,更加深入关注学生自发地去发现,鼓动学生大胆地提出自己学习的新见解,归纳出结论或感悟出规律,以生活思维和数学思维的节点为突破口,激发学生的兴趣。
四、合理分组进行有效交流
合理分组,是根据学生学习成绩、能力、兴趣不同,按“组间同质,组内异质”的原则编组,组内设正副助教。“组内异质”为小组成员内部互相帮助提供了前提,而“组间同质”又为各小组间公平竞争提供了保证。
有效交流,可集思广益,互相启发,加深理解,提高认识,激发学习热情,重在“有效”。 首先,在展示体验中激发互相交际的欲望;其次,在交流体验中分享表现乐趣;再次,在自说体验中感悟数学之理。关注学生在课堂中学习的行为表现,尤为重视师生、生生间的有效互动,积极拓宽学生的活动空间,丰富课堂教学的组织形式。开展师生合作学习,使教学和谐发展,将教师的导和学生的学贯穿在教学之中,使学生亲身体验与探究。
五、一题多变培养创新能力
创新是一个民族的灵魂,是一个国家兴旺发达的不竭动力。数学是开发学生智力的一门学科,也是培养学生创新能力的基础课程。在数学教学中要使数学知识本身逻辑系统和学生认知规律的相互作用下,能上下、左右、前后各个方向整合,纵向分化,横向综合,使各部分知识纵横联系,相互促进,广中求深。发展思维能力是培养能力的核心,培养创新思维,就要让学生“大胆求异”。我们以变化题目的条件,或变化题目的结论,或条件和结论同时变化等形式培养学生,可加深对题目之间规律的认识,开创学生的思维。因此,在教学中我们要做好以下三变:
1.变化题目的条件
如在两个圆的位置关系中,有多种情况,但反映到某类题目中,却可以得到许多相同的结论,这对研究有关的问题是很有益的。
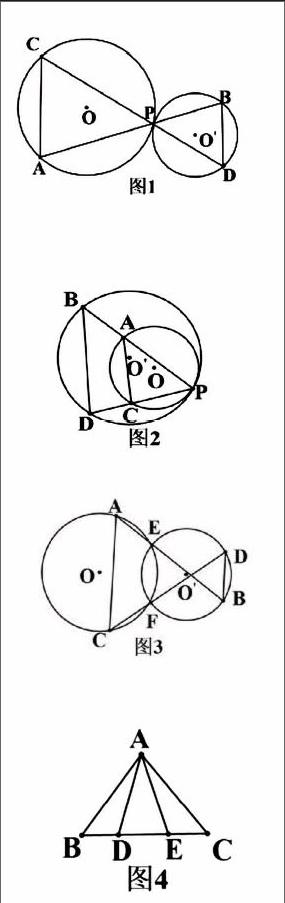
例1 已知:如图1,☉O和☉O′外
切于P,过P作两条直线AB与CD,分别
交☉O于A,C;交☉O′于B,C.
求证:AC//BD.
例2 已知:如图2,☉O和☉O′内切
于点P,过P点做两条直线PAB和PCD,分
别交☉O于A,C;交☉O′于B,D.
求证:AC//BD.
例3 已知:如图3,☉O和☉O′相交
于E,F 分别作直线AB,CD,交☉O
于A,C,交☉O′于B,D.
求证:AC//BD.
2.变化题目的结论
例4 如图4,点D,E在ABC的BC
上,AB=AC,AD=AE.
求证:BD=CE.
可变化为:(1)上题已知条件不变,
求证:BAD=CAE.(2)上题已知条件不变,求证:BE=CD.
3.条件和结论同时变化
例 化简■(a<3).
可将它变成:(1)填空:当■=a-3时,a的取值范围是 。
(2)选择:当a≤5时,化简■结果是( )
(A)a-5 (B)5-a
(C)5+a (D)以上都不对
(3)化简■(x<0) ;(4)化简■(a<6)
(5)化简■(a≥2)
总之,五个有效课堂教学方法,既关注到整体学生素质的提高,又使不同层面学生得到不同发展,实现了知识由“外”向“内”转化,激发了学生的学习兴趣,培养了学生自主学习、合作学习的好习惯和创新思维能力,是提高数学教学质量的好途径。

