基于信号共振稀疏分解和最大相关峭度解卷积的齿轮箱故障诊断

何 群 郭源耕 王 霄,2 任宗浩 李继猛

1.燕山大学电气工程学院,秦皇岛,0660042.秦皇岛港股份有限公司第六港务分公司，秦皇岛，066004



基于信号共振稀疏分解和最大相关峭度解卷积的齿轮箱故障诊断

何 群1郭源耕1王 霄1,2任宗浩1李继猛1

1.燕山大学电气工程学院,秦皇岛,0660042.秦皇岛港股份有限公司第六港务分公司，秦皇岛，066004

当齿轮箱内旋转零件发生故障时，其振动信号中的故障脉冲成分易被箱体中其他旋转部件的谐波信号和背景噪声所淹没，故障特征难以被有效提取。针对这一问题，提出了基于信号共振稀疏分解和最大相关峭度解卷积的故障诊断方法。该方法首先通过信号共振稀疏分解将信号中的低共振冲击成分从谐波分量和噪声中分离，然后对低共振分量进行最大相关峭度解卷积计算，进一步突出低共振分量中的周期脉冲成分，最后通过包络谱分析进行故障诊断。算法仿真、实验分析和工程应用结果表明,该方法能够有效提取强噪声信号中的周期性冲击成分，凸显故障特征，从而提供准确可靠的诊断结果。

齿轮箱；故障诊断；信号共振稀疏分解；最大相关峭度解卷积；冲击特征提取

0 引言

齿轮箱作为广泛应用于机械设备中的传动部件，在动力和旋转运动的传递过程中发挥着至关重要的作用。近年来,随着机械设备不断向高负载、高转速的方向发展，人们对齿轮箱可靠性提出了更高要求。齿轮箱是由轴、轴承和齿轮等旋转零件构成的整体，其工作过程中产生的振动信号包含了丰富的运行状态信息。齿轮箱运行时振动信号以谐波为主，当它某一部件损坏时振动信号的故障特征多以周期性脉冲形式体现[1-2]，这些周期性脉冲可以作为旋转零件是否存在故障的评判标准。在工程实际中，对于齿轮箱振动信号的采集要根据被测物的实际情况放置测点，采集到的信号往往会受到其他结构的影响，故障脉冲常常淹没于谐波信号和背景噪声中，故障特征难以被提取出来，因此如何从复杂的振动信号中提取周期性脉冲信息是齿轮箱故障诊断的关键。

针对该问题，很多学者进行了深入研究，提出了多种的解决方法。文献[3]利用经验模态分解(EMD)方法将复杂的多分量振动信号自适应分解成若干个本征模态分量(IMF)，然后从IMF中提取故障特征；为确定由故障引起的共振调制边频带，文献[4]提出了共振解调结合小波包系数熵阈值降噪的综合算法；文献[5]将线调频小波路径追踪算法与阶比循环平稳解调方法相结合，实现了变转速下轴承故障的检测；文献[6]利用信号共振稀疏分解和能量算子解调相结合的方法，将信号分解为高、低共振分量，进一步用Teager能量算子对不同分量下的信号进行解调分析，实现齿轮箱复合故障诊断；文献[7]通过角域重采样的方式将变转速信号变换为恒定转速信号，然后运用最大相关峭度解卷积方法实现了变转速下的轴承早期故障诊断；文献[8]将相关峭度为评价指标，实现了基于自适应随机共振和稀疏编码算法的齿轮故障诊断。

信号共振稀疏分解(RB-SSD)方法最早由SELESNICK提出[9]。该方法通过品质因子可调小波变换分别建立高低共振分量的稀疏表示，再利用形态学分析方法建立稀疏分解的目标函数，并通过分裂增广拉格朗日收缩算法，将信号中的瞬态冲击成分和持续振动成分进行分离。当齿轮箱故障发生时，故障信息往往以周期性脉冲形式体现在振动信号中，信号共振稀疏分解理论上能够有效地将振动信号中的谐波成分和冲击成分进行分离，使故障脉冲得以凸显[10]，然而齿轮箱结构复杂，故障信号中谐波和噪声干扰强烈，RB-SSD方法中仅通过单一的小波字典无法有效地对其进行分解，低共振分量中仍会混有干扰成分。最大相关峭度解卷积(MCKD)方法由MCDONALD等[11]提出，该方法考虑到信号中冲击成分的周期性，以相关峭度最大化为目标，剔除无关成分，从而有效地突出当前解卷周期下的连续脉冲序列。本文针对受背景噪声和谐波干扰强烈的周期性脉冲信号难以提取的问题，提出了基于信号共振稀疏分解和最大相关峭度解卷积的故障诊断方法。

1 齿轮箱冲击故障特征提取方法

1.1 信号共振稀疏分解

信号共振稀疏分解理论根据品质因子Q值的高低对信号中的谐波成分和脉冲成分进行分离，使故障脉冲得以凸显。品质因子Q可用来定义信号共振属性的高低，高共振信号频率聚集性好，Q值较高；低共振信号的时间聚集性好，Q值较低。瞬态的冲击信号为宽带信号，具有低的品质因子；持续振荡的周期信号为窄带信号，具有高的品质因子[12]。

假定观测信号x可表示为两个信号x1、x2的叠加，即

x=x1+x2x,x1,x2∈RN

(1)

则信号x1、x2可以通过具有低相关性的基函数库或框架S1、S2进行表示，信号共振稀疏分解方法中S1、S2分别由高/低品质因子可调的小波滤波器组组成[12]。信号分解过程中的目标函数为

(2)

其中，W1、W2分别为信号x1、x2在框架S1、S2下的变换系数；正则化参数λ1、λ2的取值分别影响高共振分量和低共振分量的能量分配，单独增大其中一个λ值，会使其对应分量的能量减小，而同时增大λ1、λ2的值会使残余信号的能量增大。

(3)

1.2 最大相关峭度解卷积

峭度是一种能够反映冲击变量分布特性的数值统计量，可有效地反映振动信号的分布特性，对冲击信号尤为敏感，但是峭度指标无法有效地提取特定的周期成分[13]。相关峭度指标是在峭度基础上提取出的概念，相关峭度的表达式为

(4)

式中，y为原始信号；N为信号长度；M为周期偏移数；T为冲击周期。

从式(4)中可以看出，相关谱峭度的定义引进了周期参数T，充分地考虑了信号中冲击成分的连续性，能更准确地衡量信号中的周期脉冲成分。

假设信号y是一个连续脉冲，x是冲击信号经过周围环境和路径传输后采集到的实测响应信号，那么上述过程可以由下式表示：

x=h*y+e

(5)

为了便于分析，暂时不考虑噪声e的干扰，则输入xn信号的解卷积过程为

(6)

式中，L为有限脉冲响应(FIR)滤波器的长度；Fk为FIR滤波器的系数。

在解卷积过程中以相关峭度最大化作为评定指标，则算法的目标函数为

(7)

优化问题的求解等价于求解方程

(8)

将通过式(8)得到的滤波器代入式(6)，便得到了以相关峭度最大为目标的解卷积结果，其结果充分考虑了信号的周期性，使周期为T的脉冲信号能够被有效提取。

1.3 算法流程

在强背景噪声下，信号共振稀疏分解方法分离出的低共振分量中会混有较强的无关冲击成分。相关峭度充分考虑到信号中冲击成分的周期性，能够有效地突出信号中的周期性脉冲成分。在本文中，通过引入最大相关峭度解卷积的方法对低共振脉冲分量进行进一步处理，根据先验信息对周期T进行设定，实现低共振分量中周期脉冲信号的提取。算法流程如下：

(1)运用RB -SSD方法对原始振动信号进行分析得到高共振分量和低共振分量，剔除信号中高共振谐波分量的影响，使脉冲成分集中体现于低共振分量中。

(2)通过MCKD方法处理RB -SSD分解后得到的低共振分量，使分量中的周期性脉冲信号得以凸显。最大相关峭度解卷积方法中的相关参数根据齿轮箱的结构参数和采样频率等信息确定。

(3)对MCKD处理后的低共振分量进行包络解调分析，根据包络谱诊断齿轮箱故障。

2 仿真信号分析

为验证本方法的有效性，模拟被谐波干扰和背景噪声淹没的周期性故障信号，建立如下仿真信号：

(9)

其中，h(t)为故障冲击成分，由i个幅值B=1的脉冲构成(图1a)，其衰减系数C为-1000，共振系数fn为2000，冲击间隔T1为0.02 s，即故障频率为50 Hz；s(t)为谐波干扰(图1b)，由幅值A1=A2=1，频率f1=450 Hz，f2=1200 Hz的正弦信号叠加而成，用以模拟齿轮箱中多种谐波信号；n(t)为高斯白噪声。

故障仿真信号x(t)由上述3种信号叠加而成。由下式计算信噪比：

(10)

式中，n2(n)为噪声的能量。

计算可得故障冲击h(t)相对于信号中的其他成分的信噪比为-11 dB。信号采样频率为10 000 Hz，采样点数为1024。信号波形如图1c所示。

(a)脉冲信号

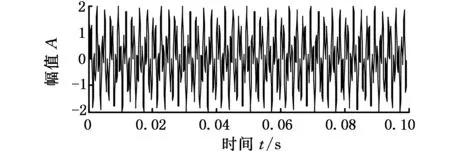
(b)正弦信号

(c)合成信号图1 仿真信号时域波形Fig.1 Waveforms of simulation signal

从合成信号的时域图谱中可以发现，冲击成分完全被淹没，无法从时域信号中辨别故障信息。对仿真信号x(t)作Hilbert变换并计算其包络谱，如图2所示，发现包络谱中峰值频率为752 Hz，约为谐波信号f2与f1的差值，图2所示的包络谱低频部分未出现冲击信号相关的频率或其倍频成分。

图2 仿真信号包络谱Fig.2 Hilbert envelope spectrum of simulation signal

为了实现原始信号中周期性脉冲的增强提取，首先对信号x(t)进行信号共振稀疏分解。将信号分解为包含谐波成分的高共振分量和包含脉冲信号成分的低共振分量，结果如图3所示。图3a和图3b分别代表信号中的高共振谐波成分和低共振脉冲成分，可见谐波成分被有效地从原始信号中分离出来，但是低共振信号中冲击成分的周期性并未体现，难以通过低共振分量对故障进行判断。

(a)高共振分量

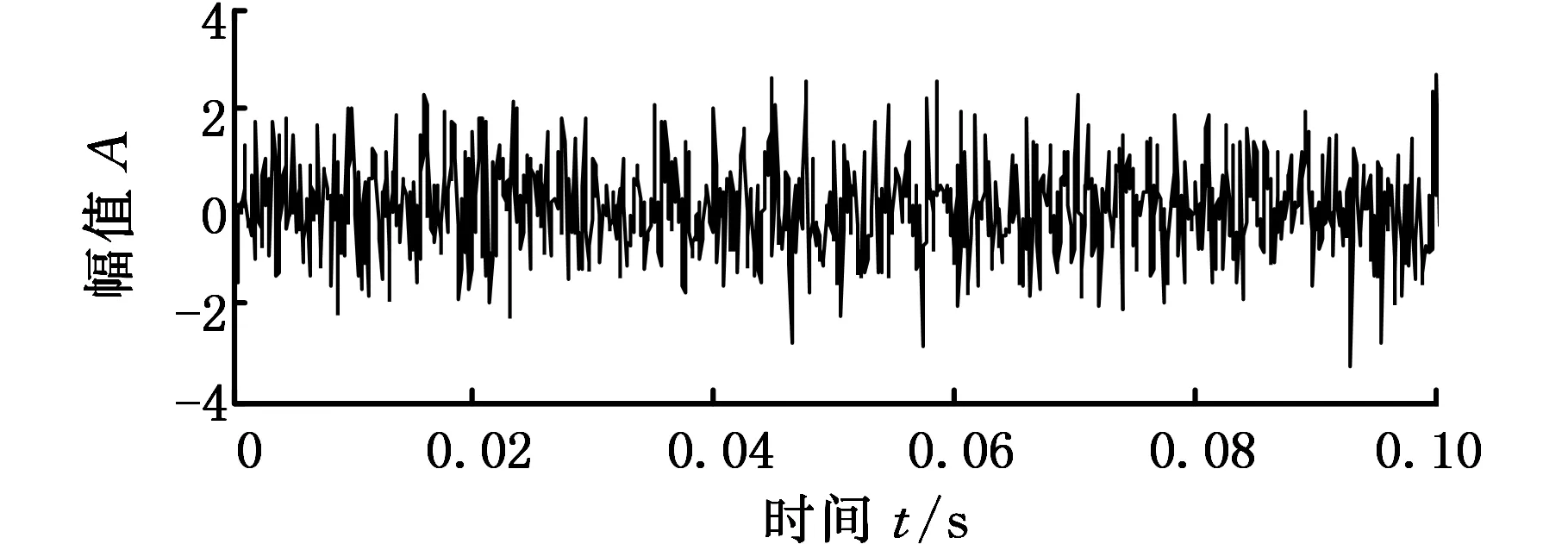
(b)低共振分量图3 信号共振稀疏分解结果Fig.3 Results of the simulation signal analyzed using the RB-SSD method

为了凸显低共振分量中的周期脉冲成分，采用最大相关峭度解卷积方法对低共振分量进行进周期解卷。解卷积参数周期根据被测对象的转频和采样频率计算得到T=200。解卷积结果如图4所示，可以明显看出，低共振分量中明显出现了周期近似为0.02 s的冲击序列，与仿真信号中频率为50 Hz脉冲序列相符，仿真结果表明该方法能够有效地提取信号中的周期性冲击成分。

图4 低共振分量解卷积结果Fig.4 The result of low-resonance analyzed using the MCKD method

3 实验分析

利用齿轮箱故障实验数据来验证所提出的故障诊断方法。数据从实验室的风电动力传动实验台测得，如图5所示，该实验台由变频器、电动机、齿轮箱、发电机和电力负载箱组成，主要用于模拟风电动力传动系统的运行。电动机产生的转速经齿轮箱加速后作用于后续的发电设备，所产生的电能由负载箱消耗。齿轮箱结构如图6所示，采用减速箱倒置的方法来模拟风电机组中的增速齿轮箱，齿轮箱中存在如轴、齿轮、轴承等多个旋转零件，均会产生谐波信号。实验时，对高速轴上齿轮的某一齿进行切除，去掉齿宽的1/3来模拟断齿故障。振动传感器垂直放置于靠近高速轴的箱体上，用以采集高速轴径向的振动信号。高速轴输入转速为300 r/min，信号采样频率为5000 Hz，采样点数为4096。

图5 实验平台Fig.5 The test stand

图6 齿轮箱内部结构Fig.6 The structure of the gearbox

齿轮箱断齿故障信号如图7a所示，故障特征被完全掩盖，无法直接识别故障。采用本文所提出的方法首先对信号进行信号共振稀疏分解，对齿轮箱振动信号中由旋转部件产生的谐波和周期性故障脉冲进行分离，得到图7b和图7c所示的高共振分量和低共振分量。其中低共振分量包含大量的冲击成分，但整体的规律性脉冲成分并不明显，不能作为故障诊断的依据。

随后进一步对低共振分量进行最大相关峭度解卷积处理，相关参数T通过齿轮箱结构计算出的转频信息结合采样频率得到，T=1002，解卷积结果如图8a所示。从图8a中可以明显看到周期近似为0.203 s的冲击序列，经计算得到其频率为4.95 Hz，接近高速轴转频，与高速轴齿轮故障的特征频率相符。作为对比，相同参数下传统的MCKD处理结果如图8b所示，可以发现处理结果中并未出现明显的周期性脉冲，无法根据检测结果给出明确的诊断结论。实验结果证明,采用所提方法通过谐波信号和冲击信号的分离和对周期性脉冲的增强提取，能够实现齿轮箱断齿故障的有效准确检测。

(a)原始信号

(b)高共振分量

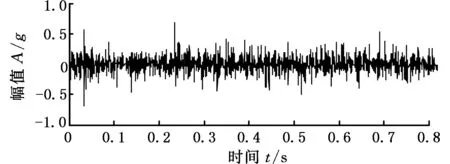
(c)低共振分量图7 断齿故障信号共振稀疏分解处理结果Fig.7 Results of the vibration signal analyzed using the RB-SSD method

(a)低共振分量MCKD结果

(b)传统MCKD结果图8 断齿故障解卷积处理结果Fig.8 Results of the signal analyze using the MCKD method

4 工程应用

风能作为一种可再生能源近年来发展迅速，但是由于风力发电设备长期运行于偏僻环境中，设备更换成本巨大，从而对风力发电设备的安全性检测提出了更高的要求。齿轮箱作为风力发电设备中重要的动力传动装置，工作环境恶劣，容易发生故障，严重影响风机的运行。为避免风机发生重大事故，实现风力发电机齿轮箱早期故障识别与诊断具有重大的意义。

振动信号来源于某风力发电机组在线检测信号，风机内部机构由异步发电机和一级行星齿轮箱构成。采用加速度振动传感器对风机进行检测，分别放置在发电机前后轴承、主轴前后轴承、齿轮箱输入端和输出端，采样频率为12.8 kHz。

对测得振动信号的初步分析发现，齿轮箱输出端轴承的振动幅值对比其他测点较大，随之对其进行进一步分析。轴承型号为6324，通过转速计测得该风机的工作转速约为1500 r/min。根据转速信息和轴承型号计算得到轴承的相关故障特征频率，见表1。

表1 转速为1500 r/min的6324轴承故障特征频率Tab.1 Fault features of the bearing 6324 at 1500 r/min

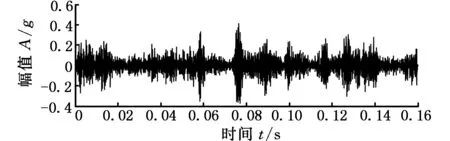
图9为齿轮箱输出端振动信号时域波形。由于风机结构复杂，振动信号中包含系统中大量的谐波成分,加之运行环境恶劣、背景噪声强烈，故障特征信息被完全淹没。在图10所示的Hilbert包络谱中，也只出现了25 Hz左右的转频，并未出现故障相关信息。

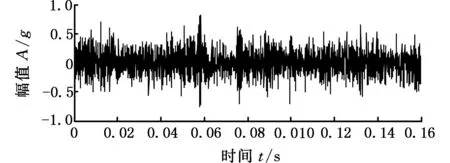
图9 振动信号时域波形Fig.9 The waveform of the vibration signal

图10 振动信号包络谱Fig.10 The Hilbert envelope spectrum of the vibration signal

采用所提方法对信号进行分析，首先对原始信号进行信号共振稀疏分解去除信号中的谐波干扰和噪声成分，结果如图11所示。可以看出，低共振分量中包含大量的微弱冲击成分，但难以清晰辨别故障特征。 根据转速和采样频率等相关信息，分别选择周期T为106、161和221，对不同的MCKD结果进行筛选，经对比后发现，T=106时脉冲的提取效果明显。如图12a所示，经过本文方法处理后的信号时域波形中可以明显地看到等间隔的冲击序列，冲击周期约为0.0082 s；其Hilbert包络谱如图12b所示，清晰地出现了118.8 Hz频率及其倍频成分，与轴承内圈特征频率相符，实现了轴承故障特征的提取。作为对比，图13给出了相同参数下未经RB-SSD处理的MCKD结果，可以发现相比于本文方法，MCKD方法周期性脉冲提取效果并不显著，无规律可循，无法根据检测结果给出明确的诊断结论。

(a)高共振分量

(b)低共振分量图11 信号共振稀疏分解结果Fig.11 Results of the vibration signal analyzed using the RB-SSD method

(a)低共振分量解卷积结果

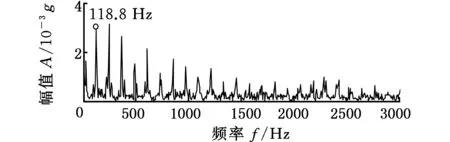
(b)处理结果包络谱图12 低共振分量解卷积结果Fig.12 Results of the vibration signal analyzed using the proposed method

图13 传统MCKD检测结果Fig.13 The result of the vibration signal analyzed using the original MCKD method

5 结 论

(1)当齿轮箱振动信号存在周期性脉冲时，预示箱体内有旋转零件发生故障，但是由于强烈谐波干扰和背景噪声的存在，周期性脉冲信号不易察觉。

(2)针对RB -SSD算法小波字典单一，对含有多种谐波成分的故障信号分解效果不理想的问题，本文将MCKD方法与之结合，实现低共振分量中周期信号的增强提取。

(3)RB -SSD和MCKD方法结合，对振动信号的采集位置要求降低，能够有效提取振动信号被谐波和噪声淹没的微弱周期性冲击成分。

(4)实验和工程应用实例表明，该方法提取齿轮箱故障信号中的周期冲击成分效果明显，为齿轮箱故障诊断提供了一种有效的解决方法。

[1] 褚福磊. 机械故障诊断中的现代信号处理方法[M].北京：科学出版社, 2009:165-170. CHU Fulei. Mechanical Fault Diagnosis of Modern Signal Processing Methods[M]. Beijing: Science Press Pub.,2009:165-170.

[2] YUAN J, HE Z, ZI Y. Gear Fault Detection Using Customized Multiwavelet Lifting Schemes[J]. Mechanical Systems & Signal Processing,2010,24(5):1509-1528.

[3] 武哲, 杨绍普,刘永强. 基于多元经验模态分解的旋转机械早期故障诊断方法[J]. 仪器仪表学报,2016,32(2):241-248. WU Zhe, YANG Shaopu, LIU Yongqiang. Rotating Machinery Early Fault Diagnosis Method Based on Multivariate Empirical Mode Decomposition[J]. Chinese Journal of Scientific Instrument, 2016,32(2):241-248.

[4] 崔玲丽, 康晨晖, 张建宇,等. 基于时延相关及小波包系数熵阈值的增强型共振解调方法[J]. 机械工程学报, 2010,46(20):53-57. CUI Lingli, KANG Chenhui, ZHANG Jianyu, et al. Enhanced Resonance Demodulation Based on the Delayed Correlation and Entropy Threshold of Wavelet Packet Coefficients[J]. Journal of Mechanical Engineering, 2010,46(20):53-57.

[5] 徐亚军, 于德介, 刘坚. 基于线调频小波路径追踪阶比循环平稳解调的滚动轴承故障诊断[J]. 航空动力学报, 2013,28(11):2600-2608. XU Yajun, YU Dejie, LIU Jian. Fault Diagnosis of Roller Bearings Based on Chirplet Path Pursuit and Order Cyclostationary Demodulation[J]. Journal of Aerospace Power, 2013,28(11):2600-2608.

[6] 张文义, 于德介, 陈向民. 齿轮箱复合故障诊断的信号共振分量能量算子解调方法[J]. 振动工程学报, 2015,28(1):148-155. ZHANG Wenyi, YU Dejie, CHEN Xiangmin. Energy Operator Demodulating of Signal’s Resonance Components for the Compound Fault Diagnosis of Gearbox[J]. Journal of Vibration Engineering, 2015,28(1):148-155.

[7] 任学平, 张玉皓, 邢义通,等. 基于角域级联最大相关峭度反褶积的滚动轴承早期故障诊断[J]. 仪器仪表学报, 2015,36(9):2104-2111. REN Xueping, ZHANG Yuhao, XING Yitong, et al. Rolling Bearing Early Fault Diagnosis Based on Angular Domain Cascade Maximum Correlation Kurtosis Deconvolution[J]. Chinese Journal of Scientific Instrument,2015,36(9):2104-2111.

[8] 李继猛,张金凤,张云刚,等. 基于自适应随机共振和稀疏编码收缩算法的齿轮故障诊断方法[J]. 中国机械工程,2016,27(13):1796-1801. LI Jimeng，ZHANG Jinfeng，ZHANG Yungang, et al. Fault Diagnosis of Gears Based on Adaptive Stochastic Resonance and Sparse Code Shrinkage Algorithm [J]. China Mechanical Engineering, 2016,27(13):1796-1801.

[9] SELESNICK I W. Resonance-based Signal Decomposition: a New Sparsity-enabled Signal Analysis Method[J]. Signal Processing, 2011,91(12):2793-2809.

[10] 陈向民, 于德介, 李蓉. 基于信号共振稀疏分解与重分配小波尺度谱的转子碰摩故障诊断方法[J]. 振动与冲击,2013,33(13):27-33. CHEN Xiangmin, YU Dejie, LI Rong. Rub-impact Diagnosis of Rotors with Resonance-based Sparse Signal Decomposition and Reassigned Wavelet Scalogram [J].Journal of Vibration & Shock,2013,32(13):27-33.

[11] MCDONALD G L, ZHAO Q, ZUO M J. Maximum Correlated Kurtosis Deconvolution and Application on Gear Tooth Chip Fault Detection[J]. Mechanical Systems & Signal Processing, 2012,33(1):237-255.

[12] SELESNICK I W. Wavelet Transform with TunableQ-factor[J]. Signal Processing IEEE Transactions on, 2011,59(8):3560-3575.

[13] 张永祥, 王孝霖, 张帅,等. 基于奇异值分解和相关峭度的滚动轴承故障诊断方法研究[J]. 振动与冲击, 2014,33(11):167-171. ZHANG Yongxiang, WANG Xiaolin, ZHANG Shuai, et al. Rolling Element Bearing Fault Diagnosis Based on singular Value Decomposition and Correlated Kurtosis[J].Journal of Vibration & Shock, 2014,33(11):167-171.

(编辑 袁兴玲)

Gearbox Fault Diagnosis Based on RB-SSD and MCKD

HE Qun1GUO Yuangeng1WANG Xiao1,2REN Zonghao1LI Jimeng1

1.School of Electrical Engineering, Yanshan University, Qinhuangdao,Hebei,066004 2.The Sixth Branch of Qinhuangdao Port Co., Ltd., Qinhuangdao,Hebei,066004

When a rotating part of the gearbox failed, the periodic fault impulse components in the vibration signals were easily submerged by the harmonic components and the strong background noises, thus leading to the challenging difficulties in the fault feature extractions. To address this issue, a new fault diagnosis method was proposed based on RB-SSD and MCKD herein. Firstly, the low-resonance components of the signals were separated from the harmonic components and the noises using RB-SSD method, and then the MCKD method was employed to the low-resonance components to further highlight the periodic impulse components. Finally, the envelope spectrum analysis was performed to diagnose the faults. The evaluation results from simulations, experiments and engineering applications demonstrate that the proposed method may extract effectively and highlight the periodic fault impulse components from noisy vibration signals, thus providing accurate and reliable diagnosis results.

gearbox; fault diagnosis; resonance-based sparse signal decomposition(RB-SSD); maximum correlated kurtosis deconvolution(MCKD); impulse feature extraction

2017-02-13

国家自然科学基金资助项目(51505415)；河北省自然科学基金资助项目(F2016203421)

TH113；TP206.3

10.3969/j.issn.1004-132X.2017.13.003

何 群，男，1969年生。燕山大学电气工程学院副教授。主要研究方向为风力发电机并网技术、故障诊断等。E-mail：hq@ysu.edu.cn。郭源耕，男，1991年生。燕山大学电气工程学院硕士研究生。王 霄，男，1982年生。燕山大学电气工程学院博士研究生，秦皇岛港股份有限公司第六港务分公司高级工程师。任宗浩，男，1991年生。燕山大学电气工程学院硕士研究生。李继猛，男，1984年生。燕山大学电气工程学院讲师。