雷诺数对增升装置流动特性影响的计算研究 Ⅰ
——气动力特性和汇流边界层
刘亦鹏 高云海 王继明 郭传亮 焦仁山 / LIU Yipeng GAO Yunhai WANG Jiming GUO Chuanliang JIAO Renshan(. 上海飞机设计研究院,上海 00; . 中国航空工业空气动力研究院,哈尔滨 5000)(. Shanghai Aircraft Design and Research Institute, Shanghai 00,China; . Chinese Aerodynamics Research Institute of Aeronautics, Haerbin 5000, China)
雷诺数对增升装置流动特性影响的计算研究 Ⅰ
——气动力特性和汇流边界层
刘亦鹏1高云海1王继明1郭传亮1焦仁山2/
LIU Yipeng1GAO Yunhai1WANG Jiming1GUO Chuanliang1JIAO Renshan2
(1. 上海飞机设计研究院,上海 201210; 2. 中国航空工业空气动力研究院,哈尔滨 150001)
(1. Shanghai Aircraft Design and Research Institute, Shanghai 201210,China; 2. Chinese Aerodynamics Research Institute of Aeronautics, Haerbin 150001, China)
在1×106~30×106的雷诺数范围内,马赫数为0.197的情况下,使用数值计算方法研究了雷诺数对NHLP-2D翼型的气动力特性和流动特性的影响。建立的数值模型考虑了汇流边界层的网格处理,与已有试验和计算结果对比分析表明本数值模型可信。计算结果表明,当雷诺数大于1.5×107时,雷诺数对气动力系数的影响明显减小,且小迎角下气动力随雷诺数呈线性变化趋势。汇流边界层高度随雷诺数增大而降低,缝翼和主翼产生的尾迹强度随雷诺数的增大而减弱,同时尾迹宽度逐渐减小。在高雷诺数下,襟翼尾缘处仍存在较强的缝翼尾迹,说明尾迹/边界层的相互融合作用随雷诺数增大而减小。本文为后续雷诺数对缝道流动特性的影响研究提供了基础。
增升装置;雷诺数;汇流边界层;数值模拟
0 引言
增升减阻对民用飞机设计具有重要意义,民用飞机增升主要通过增升装置设计来实现。增升装置高升力构型的几何形状较为复杂,流动会产生很强的尾迹/边界层干扰。因此,高升力系统空气动力特性的研究一直是民机研究的前沿课题。高升力外形数值计算中必须能捕获流动的典型特征,图1[1]给出了二维三段翼型绕流中可能呈现的各种流动物理现象,它们都是在流体力学中令人困扰并难以解决的复杂流动现象,要正确求解每一项都很困难,而要综合各项在一起求解更是一项难以应付的工作[2]。缝隙的黏性流动使每个翼段都生成各自的尾迹,它们既对下游翼段吸力峰值提供阻尼而减弱分离的可能,又与下翼段的边界层相互作用,形成汇流边界层而增加分离的倾向。因此,高升力多段翼型流动计算必须综合考虑无黏流动与有黏流动的不同影响,以寻求最佳的缝隙尺寸[3]。
由于高升力多段翼型流动的复杂性,基于CFD方法的高效准确数值模拟研究一直在进行。Brune和Mamsters[4]认为,诸如网格生成,分离流的湍流模拟,层流向湍流的过度等方面在二维问题的模拟计算得到充分验证后,才可以进一步尝试将相应的方法向三维问题推广。Smith[2]的研究表明,在二维情况得到验证的方法,一般在三维问题中仍能够保持较好的精度。除了诸如展向流动、飞机部件间的黏性干扰等个别情况,二维CFD方法对高升力问题的求解都能够起到基础作用。从实用角度而言,二维CFD分析对于理解高升力多段翼型流动特性随雷诺数和几何外形的变化也是非常有帮助的[2]。
国内学者对高升力构型的气动力随雷诺数的变化规律开展过一些研究。文献[5] 在中等雷诺数条件下,用试验的方法研究了GAW-1两段翼型缝道参数随雷诺数变化的规律。研究发现,雷诺数在1×106~2×106范围内,缝道宽度随雷诺数增大而减小,ΔGap=-0.00154cΔRe。然而,这种规律是建立在变来流速度基础上的变雷诺数试验,因此试验结果不可避免地包含了马赫数的影响。而更加关注的问题是当马赫数不变时,流动特性随雷诺数的变化规律,进而探索一个根本问题,即在雷诺数较低的风洞试验条件下得到的最优高升力构型,在飞行雷诺数条件下是否还是最优构型;或是,针对某种高升力构型,至少应进行多大雷诺数的风洞试验,才能将得到的风洞试验结果有效地外推至飞行雷诺数的结果。因此,本文将在定马赫数条件下研究雷诺数对气动力、压力分布、汇流边界层、缝道流动特性的影响。由于篇幅所限,雷诺数对缝道流动特性的影响将在后续文章《雷诺数对增升装置流动特性影响的计算研究Ⅱ——缝道流动特性》中进行详细分析。
1 研究对象
用于研究的多段翼型应当是接近真实飞机的翼型,其绕流应当较为复杂,包括流动分离、尾迹和边界层干扰等现象。该翼型应当有可信的风洞试验数据,以便和计算结果进行比较。基于这样的考虑,本文采用已被广泛研究的NHLP-2D翼型的L1 T2构型[6]。作为英国National High-Lift Programme项目中的一部分,该翼型于1970年代早期在BAC风洞进行过试验。基于BAC风洞具有高精度的二元流场特征,试验数据达到了较高的精度,有利于验证计算。使用文献[6]给出的坐标点,通过样条曲线重构翼型,如图2所示。
有关该翼型试验数据来源于文献[7]中的Case 2。包括翼型的升力系数、阻力系数,表面压力分布,以及垂直于翼型表面的总压分布等,这些数据被广泛地应用于CFD方法验证分析。
2 计算方法
本文采用商业CFD软件求解NHLP-2D翼型的绕流。控制方程使用二维可压缩雷诺平均N-S方程,使用有限体积法离散控制方程。湍流模型使用了SSTk-ω模型[8]和SA模型[9],并比较了两种湍流模型对计算结果的影响。翼型表面为无滑移绝热壁面条件,流场边界使用压力远场边界条件。计算残差收敛精度小于10-7。
3 计算网格和边界条件
Rumsey[1]指出,阻力系数对于远场边界较为敏感。为更好模拟尾迹区域的流动,正确地计算阻力,远场边界应至少置于50c处(c为翼型弦长)[10-11],甚至50c~60c[12]。本文计算远场边界选为60c。表面网格密度,本文选取0.2%c。对于翼型后缘厚度为0.7%c~1%c,网格密度为0.03%c,节点数为20~30个。对于尾迹区,以及尾迹和边界层相互作用的区域,文献[13]指出应使用均一化的细网格进行处理,但其只在翼型下游的水平方向上进行了尾迹区的划分(如文献[13]中图5所示)。显然,这种尾迹区的网格策略更加适合特定迎角的情况,对于本文涉及的变迎角情况,一个扇形的尾迹区更加合理,本文尾迹区网格如图3所示。
边界层布置30个节点,增长率1.2,第一层网格高度由下式给出[13]:

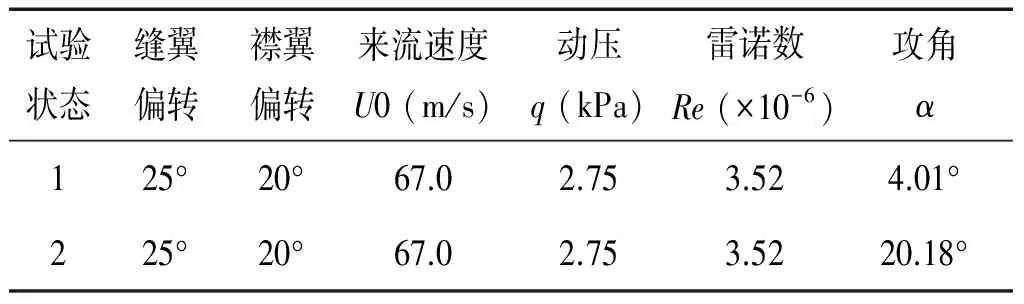
表1 用于计算验证的NHLP-2D试验状态[7]
4 计算结果与分析
4.1 计算结果与文献结果的对比
使用建立的细网格计算了翼型的气动力特性,比较了SST和SA两种湍流模型,离散格式均为二阶迎风格式。图4~图6分别给出了本文计算得到的NHLP-2D翼型升力系数、阻力系数、俯仰力矩系数和已有试验结果、已有计算结果的对比。可以看出,SA模型较SST模型的计算结果更接近于试验值,适于计算高升力构型,说明本文采用计算模型计算翼型的气动力特性可行。
本文针对α=4.01°和α=20.18°情况下,计算了SST、SA两种湍流模型和一阶、二阶离散格式对翼型表面压力系数Cp分布的影响,如图7、图8所示。对于二阶精度,SST模型和SA模型计算结果基本一致,都与试验结果吻合较好,当α=20.18°时,SA模型在主翼吸力峰处略高于SST模型,更加接近试验值。当α=20.18°时,一阶精度的湍流模型均与试验值偏差较大。离散精度对Cp分布影响较大,湍流模型对Cp影响很小,在相同的离散精度下,SST模型和SA模型计算结果基本一致。综上,二阶精度的SA模型计算准度最好。
图9、图10给出了二阶精度的SA模型与文献[15]和文献[14]计算的压力分布的对比,在缝翼和襟翼处,本文计算结果与试验值更加接近,主翼前缘吸力峰处文献结果稍好于本文结果。总体而言,本文计算得到的Cp略好于文献结果。
风洞试验中测量了垂直于翼型表面曲线的总压系数(Cptot)分布,测量位置为位于主翼上的x/c=0.35,位于襟翼上的x/c=0.91,x/c=1.066(50%襟翼弦向),x/c=1.214(襟翼后缘),如图11所示。通过比较这些位置的总压系数分布,可以分析后缘尾迹与当地边界层的混合现象。
图12~图15分别给出了计算得到的α=4.01°和20.18°时翼型表面Cptot与试验结果、文献计算结果的对比。当α=4.01°时,x/c=0.35处的试验结果表明,此处的缝翼产生的尾迹宽度较窄,且强度很弱,二阶计算格式得到的尾迹仍然较强,一阶格式得到的尾迹较二阶格式弱,且显示出更强的尾迹和边界层混合效果,这和文献[15]的结论相同。x/c=0.91,x/c=1.066,x/c=1.214处的Cptot分布表明,二阶精度的SST模型给出了最强的主翼尾迹,二阶精度的SA模型和试验结果最接近。图13给出了与文献[15]计算结果对比,在4个弦向位置上,文献[15]都预测了一个更强的缝翼尾迹,与试验结果偏差较大,而本文计算结果给出了更弱的缝翼尾迹,在50%的襟翼弦长处,缝翼尾迹基本消失,和试验结果更加吻合,说明本文的计算模型更好得预测了尾迹和边界层的混合过程。
图14给出了当α=20.18°时的Cptot,两种湍流模型的一阶离散格式均与试验结果产生了很大偏离,二阶精度更接近于试验结果。在襟翼上表面,计算结果成功捕捉了缝翼和主翼的尾迹,尾迹强度预测较好,高度略低于试验值。总体而言,对于缝翼和主翼尾迹位置预测上,二阶精度的SA模型好于SST模型。图15给出了与文献[14]计算结果的对比,在x/c=0.35、1.214处,本文给出的缝翼尾迹、主翼边界层厚度、主翼尾迹好于文献计算结果。x/c=0.91处,二者计算准度相当。x/c=1.066处,在尾迹位置上,文献[14]在缝翼尾迹上层和主翼尾迹下层与试验值吻合更好,在尾迹强度上,本文预测结果更接近于试验值。在整个汇流边界层的外围,来流基本不受边界层和尾迹的干扰,Cptot应该趋近于1,本研究结果和试验结果均体现了这一趋势,而文献计算结果与试验结果有一定偏差。
综上,Cptot曲线的对比分析表明,二阶精度的SA模型可较为准确地预测汇流边界层的总压分布。
4.2 雷诺数对多段翼型气动力特性的影响
本节使用二阶离散格式的SA湍流模型研究雷诺数对多段翼型的宏观流动特征和汇流边界层区域的影响。图16给出了α=4.01°和20.18°时,雷诺数对升力系数、阻力系数、俯仰力矩系数的影响。雷诺数增大,汇流边界层厚度降低,从而增大了翼型的有效弯度,升力系数随雷诺数增加而增大。阻力系数和俯仰力矩系数随雷诺数增加而减小。当雷诺数增大时,气动力系数对雷诺数的导数减小(如图17所示),雷诺数影响减弱。对比图中的两条曲线,可以看出高迎角下的雷诺数效应大于低迎角下的。当雷诺数大于1.5×107时,气动力对雷诺数的导数明显减小,且小迎角下的导数基本不变,说明气动力随雷诺数呈线性变化趋势。
图18~图20给出了当M=0.197,α=20.18°时,雷诺数对压力分布的影响。对于缝翼,上表面前缘吸力峰随雷诺数增高而增大,下表面存在稳定的分离涡,该区域随雷诺数变化很小。对于主翼,上表面速度较高,前缘吸力峰随雷诺数增高而增大,驻点位于下表面(如图21所示),且流速较低,该区域Cp随雷诺数变化很小。襟翼压力分布随雷诺数变化规律和主翼类似。
雷诺数对汇流边界层内总压系数分布的影响较为复杂,如图22~图25所示。总体而言,整个汇流边界层高度随雷诺数的增大而降低。图22、图23表明,随着雷诺数的增大,缝翼产生的尾迹在主翼上表面减弱,主翼边界层高度降低。对于襟翼上表面和襟翼后缘处,主翼产生的尾迹强度随雷诺数的增高而减弱,且尾迹宽度逐渐减小。主翼边界层外侧的Cptot与缝翼尾迹核心的Cptot的差值随雷诺数的增大而增加,说明雷诺数增高降低了尾迹的强度,同时尾迹和边界层的混合效应也随之降低。
5 结论
本文在1×106~30×106的雷诺数范围内,马赫数为0.197的情况下,使用数值方法研究了雷诺数对NHLP-2D翼型L1 T2构型的气动力特性和汇流边界层流动特性的影响。与已有试验结果的对比分析表明,二阶迎风格式的SA湍流模型计算得到的气动力特性、翼型表面Cp分布、汇流边界层内的总压系数分布和试验结果吻合较好,说明建立的数值模型可信,可用于评估雷诺数对二元增升装置流动特性的影响。
本文计算表明,升力系数随雷诺数增加而增大,阻力系数和俯仰力矩系数随雷诺数增加而减小。当雷诺数大于1.5×107时,雷诺数对气动力的影响明显减小。Cp分布表明,三段翼型的上表面前缘吸力峰均随雷诺数增高而增大。翼型下表面的稳定分离涡区域和驻点区域的Cp分布基本不随雷诺数变化。汇流边界层内的总压系数分布表明,缝翼和主翼产生的尾迹强度随雷诺数的增大而减弱,同时尾迹宽度逐渐减小,主翼、襟翼边界层高度降低。汇流边界层内的尾迹/边界层的相互混合作用随雷诺数增大而减小。本文计算采用的方法、网格处理及计算边界的选取为后续雷诺数对缝道流动特性的影响研究提供了基础。
[1] Christopher L. Rumsey, Susan X. Ying. Prediction of high lift: Review of present CFD capability [J]. Progress in Aerospace Sciences, 2002, 38: 145-180.
[2] 朱自强, 陈迎春, 吴宗成, 陈泽民. 高升力系统外形的数值模拟计算. 航空学报, 2005, 26(3), 257-262.
[3] Smith A M O. High lift aerodynamics [J]. J Aircraft, 1975, 12(6):501-530.
[4] Brune G.W. and Mamsters J. H.. Computational Aerodynamics Applied to High-Lift Systems [J]. Applied Computational Aerodynamics, Progress in Aeronautics and Astronautics, Vol. 125, 1990, Henne, P.A., Ed.
[5] 张弓. 多段翼型缝道流动的相似准则研究[D]. 西安:西北工业大学, 2007.
[6] Ian G. Fejtek. CFD 96 Computer Code Validation Challenge—multiple Element Airfoil[C]. CFD96, the Forth Annual Conference of the CFD Society of Canada, 1996.
[7] Burt M. A selection of experimental test cases for the validation of CFD codes: Chapter 5-summaries of the test cases [R]. AGARD AR-303 vol. 1, 1994, August: 55-133.
[8] Menter F. R.. Two-Equation Eddy-Viscosity Turbulence Models for Engineering Applications[J]. AIAA Journal, 1994, 32(8): 1598-1605.
[9] Spalart P., Allmaras S.. A one-equation turbulence model for aerodynamic flows[R]. Technical Report AIAA-92-0439, American Institute of Aeronautics and Astronautics, 1992.
[10] Larsson T. Separated and high lift flows over single and multi-element airfoils [C]. Proceedings ICAS 19th congress, Vol.3, 1994. 2505-2518.
[11] Cao H V, Kusunose K, Spalart P R, et al. Study of wind tunnel wall interference for multi-element airfoils using a Navier-Stokes code[C]. AIAA 94-1933, 1994.
[12] João Alves de O. Neto, Carlos B. Júnior, Darci Cavali, and João Luiz F. Azevedo. Aerodynamic study of high-lift device configurations for take-off and landing conditions[C]. 25th International Congress of the Aeronautical Sciences.
[13] Anutosh Moitra. Issues in 2-D high-lift CFD analysis: a review[C]. AIAA 2003-4072.
[14] Christopher L. Rumsey, Thoms B. GaTski, Susan X. Ying and Arild Bertelrud. Prediction of high-lift flow using turbulent closure models[C]. AIAA 97-2260.
[15] Joseph H. Morrison. Numerical study of turbulence model predictions for the MD 30P/30N and NHLP-2D three-element high lift configurations[R]. NASA/CR-1998-208967.
Calculation Research on the Effect of Reynolds Number on the High Lift Device Flow Characteristcs I—Aerodynamic Characteristics and Confluent Boundary Layer
The aerodynamic characteristics and confluent boundary layer of NHLP-2D air foil are studied within the Reynolds number range from 1×106to 30×106and Mach number 0.197 by numerical simulation. Mesh scheme in the confluent boundary layer is carefully developed in the numerical model. Comparison with the existing test data and numerical data shows the model of present study is reliable. The Reynolds number effect on aerodynamic coefficient is obviously decreased whenReis larger than 1.5×107. And areodynamic coefficient shows a linear variation with Reynolds number for small angle of attack. As increasing Reynolds number, the thickness of confluent boudary layer decreases, and the wake intensity of slat and main element decreases. The width of wake also decreases as increasing Reynolds number. The slat wake remains strong at the trailing edge of flap at high Reynolds number which implies the interaction between wake and boundary layer decreases with the increasement of Reynolds number. The present study provides foundation for the subsequent research on the effect of Reynolds number on the slot flow.
high lift device; Reynolds number; confluent boundary layer; numerical simulation
10.19416/j.cnki.1674-9804.2017.02.006
航空科学基金项目,编号:No.2015324003.
V211.74
A
刘亦鹏 男,博士,高工。主要研究方向:数值风洞技术;E-mail: 17301791030@163.com
高云海 男,硕士,助工。主要研究方向: 数值风洞技术;E-mail: gaoyunhai@comac.cc
郭传亮 男,硕士,高工。主要研究方向:风洞试验及气动数据修正分析;E-mail: guochuanliang@comac.cc
王继明 男,硕士,高工。主要研究方向:风洞试验及气动数据修正分析;E-mail: wangjiming@comac.cc
焦仁山 男,硕士,高工。主要研究方向:风洞试验技术;E-mail: caria_jiao@126.com

