复值函数的导数及其应用
□陈 欢
(陕西国际商贸学院基础部 陕西 咸阳 712046)
复值函数的导数及其应用
□陈 欢
(陕西国际商贸学院基础部 陕西 咸阳 712046)
本文研究了复值函数的分析性质,提出了复值函数单侧导数的概念。给出了复值复合函数的求导法则。证明了复值函数在一点可导必连续。给出复值函数在求解中的应用例子。
复值函数;复合复值函数;复值函数单侧导数;复值复合函数的导数
1 复值函数的概念
根据实值函数的概念,引入复值函数的概念与复合复值函数如下:
定义1.1[3]设y=φ(t)和y=ψ(t)是区间[α,b]上的实函数,是虚数单位. 如果对于区间[α,b]中的每一个实数t,有唯一复数z(t)=φ(t)+iψ(t)与它对应,则称在区间[α,b]上给定了一个复值函数,记作z=z(t),tє[α, b].
定义1.2(复合复值函数)设有一个复值函数w=f(u)与实函数u=φ(t)
w=f(u),uєD⊂R,
u=φ(t),tєE⊂R,uєR
记E*={t|φ(t)єD}∩E。若E*不为空,则对每一个t єE*,可通过实值函数u=φ(t)对应D内唯一的一个值u,而u又是通过复值函数f(u)对应唯一的一个值w。这就确定了一个定义在E*上的复值函数,它以t为自变量,w为因变量,记作
w=f[φ(t)],tєE*或w=(f ◦φ)(t),tєE*
称为复值函数f(u)和实值函数φ(t)的复合函数。并称f(u)为外函数,φ(t)为内函数,u为中间变量。复值函数f(u)和实值函数φ(t)的复合运算也可记为f ◦φ。
定义1.3 设z(t)=φ(t)+iψ(t)是定义在区间α≤t≤b上的复值函数,若φ(t)和ψ(t)均是α≤t≤b上的有界函数,则称z=z(t)是α≤t≤b上的有界复值函数。
2 复值函数的导数
定义2.1(在一点可导) 设复值函数z=z(t)在区间[α,b]的某个邻域U(t0)上有定义,若极限

存在,则称复值函数z=z(t)在t0处可导,并称该极限为复值函数z=z(t)在点t0处的导数,记作z'(t0)或者dz(t0) /dt。
定义2.2(单侧导数)设复值函数z=z(t)在区间[α, b]上一点t0的某右邻域[t0,t0+δ]上有定义,若右极限

存在,则称该极限值为z=z(t)在点t0的右导数,记作z'+(t0)。
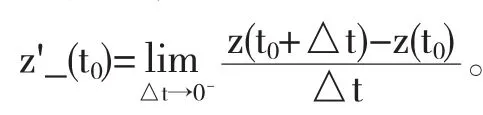
右导数和左导数统称为单侧导数。
定义2.3(在区间上可导) 如果复值函数z=z(t)在区间[α,b]上每一点都可导,且在α点存在右导数,在b点存在左导数,那么就称复值函数z=z(t)在区间[α,b]上可导。
设z1(t),z2(t)是定义在区间α≤t≤b上的可导复值函数,c是复值常数,容易验证下列复值函数的求导法则[3]:类似的,可定义左导数

3 复值复合函数的导数
定理4.1 设实函数u=r(t)在点t0可导,复值函数g=z(u)在点u0=r(t0)可导,则复值复合函数(z ◦r)(t)在t0可导,且
(z ◦r)'(t0)=z'(u0)r'(t0)=z'(r(t0))r'(t0)
定理4.2 复值函数z=z(t)在t0处可导,则它在t0处连续。
例4.1 讨论复值函数z(t)=1/t2+iet在t=1的连续性。
解 因为实函数φ(t)=1/t2和实函数ψ(t)=et在t=1处均是可导的,所以z(t)=1/t2+iet在t=1处可导,根据定理3.4可知z(t)=1/t2+iet在t=1的连续性。
结束语
本文首先引入复值函数的概念,给出了复值函数连续、单侧导数的概念以及复值复合函数的求导法则。可导性是复值函数的一个重要性质,本文还给出了复值函数在一点可导必连续,具有重要的应用价值。
[1]王高雄,周之铭,朱思铭,王寿松.常微分方程.第三版.北京:高等教育出版社,2006.
1004-7026(2017)10-0126-01
O174.1
A
10.16675/j.cnki.cn14-1065/f.2017.10.091
陕西国际商贸学院校级项目(SMXY201642)。
陈欢(1989-),女,陕西汉中人,硕士,助教,从事小波分析的研究。

