带可积时滞的非线性中立型微分方程的h-渐近稳定性

黄明辉

（广州华夏职业学院基础部，广东广州510935）

带可积时滞的非线性中立型微分方程的h-渐近稳定性

黄明辉

（广州华夏职业学院基础部，广东广州510935）

采用Krasnoselskii不动点定理证明带可积时滞的非线性中立型微分方程零解的h-渐近稳定性.进一步推广了Pinto and Sepulveda的定理，并提供了一个例子加以说明所得的结果.

h-渐近稳定；large contraction；非线性

近来，不动点理论已经成为时滞微分方程的稳定性和周期性研究的主要工具之一［1-6］.重要研究非线性中立型微分方程：

其中a（t），g（t），yi（t）和g（t,x,y）在各自定义的区间中是连续的.方程（1）的特殊形式近年来引起了许多研究者的注意［2-3,5］.本文采用Krasnoselskii不动点定理研究方程（1）零解的h-渐近稳定性，并推广Pinto and Sepulveda［3］的结论.

1 预备知识

设时滞函数di，di（t）=1-yi（t）≥0,i=1,2可以是有界或无界的时滞.定义：

考虑初始闭区间[p（τ），τ]（若p（τ）=-∞则[-∞，τ]）.对于初始条件，方程（1）为一个自然的矢量空间：BC（τ）={φ∶[p（τ），τ]→R|φ是一个有界连续函数}.

引理1x（t）=x（t,τ,φ）方程（1）的一个解当且仅当：

证方程（1）的形式重新表示为：

2 主要结果及证明

方程（1）x'（t）=a（t）x3（t）+b（t）x'（y1（t））+g（t,x（t）,x（y2（t）））中，g（t,0,0）=0,yi（t）≤t,i=1,2,t∈R.设σ∈（0，1）和Di（t）,Mi（t）=R→R+,i=1,2,定义：

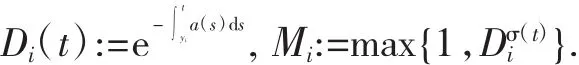
假设：（H1）（1）函数a∶R→R，满足∶

（2）y1和B=是连续可积的，yi:=R+→R是连续且：

（H2）（1）g是连续函数，x1，x2，y1，y2∈R.ε＞0，存在δ＞0和λ:R→R+，当x1-x2,y1-y2＜δ，有：

同时，存在非减连续函数v:R+→R+使得：

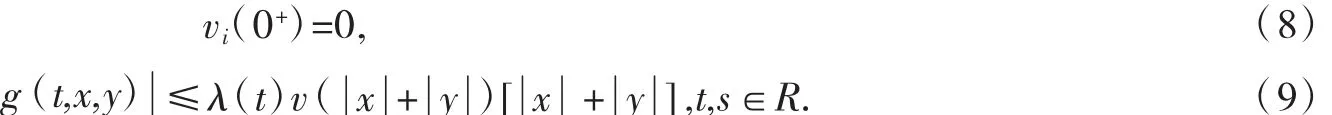
（H3）（1）对0＜σ＜1，λ和M2满足：

（2）假设：

（H4）假设：

定理1如果（H1），（H2），（H3）和（H4）成立，则方程（1）的零解是hσ-渐近稳定的，即存在σ＞0，对‖φ‖＜δ，有：

其中c=（1+‖B‖）eL(1-σ)，L是方程（4）中给定的.

显然PS⊂B.定义算子Γ1,Γ2：

下面证明Γ1S⊂S.对∀x∈S，由方程（8）、（9）和（13），选择足够小的δ，得：

因此Γ1S⊂S.下面证明Γ1是完全连续的.先证Γ1的连续性.设η＞0，由方程（7）可得，存在δ＞0，使得当x,y∈S及‖x-y‖＜δ，有：

由（H3）可得，Γ1x（t）-Γ1y（t） ＜η.

进一步证明，Γ1S在每一个紧区间上是等连续的.对x∈S，由方程（8）、（9）和（13）以及h（1u）在每个紧集都是正连续可得，对∀ε＞0，存在δ＞0，使得当t-v＜δ，有：

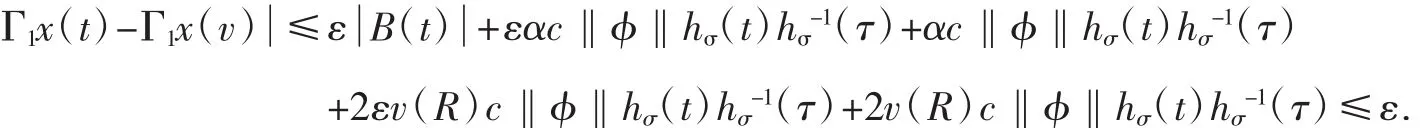
其中R=2c‖φ‖‖hσ‖.因此Γ1x在每个区间[τ,τ+n]上是等连续的以及Γ1S⊂S，故Γ1是紧算子.接下来证明，存在一个δ＞0，使得对∀x,y∈S=S（δ）,‖φ‖≤δ,有Γ1x+Γ2y∈S，即B中的一个非空凸紧集S，使得PS⊂S.

对于（H2）中的假设v，存在δ＞0，使得对‖φ‖≤δ，对x,y∈S，由方程（4）、（12）和（13）得：

所以，对∀x,y∈S,‖φ‖≤δ，选取足够小的δ，由（H3）和（H4）得：

H在上确界范数中是一个large contraction，其证明可见文献［2］.接着证明Γ2在S上是一个large contraction.对∀x,y∈S,x≠y，有‖Hx-Hy‖≤‖x-y‖.因此，由方程（4）得：

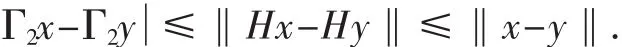
用同样的方法，存在δ∈（0,1），可证Γ2x-Γ2y≤δ‖x-y‖.及对∀ε＞0，有：

3 范例

为了说明文中的结论，下面给出中立型微分方程：

对t≥τ≥0以及初始条件x（t）=φ（t）,t≤τ.上面的中立型微分方程与（2）的形式相同，其中对给定常数β的条件，将结果应用到方程（14）可得：

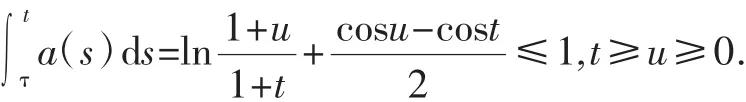
显然（H1）成立.由于：

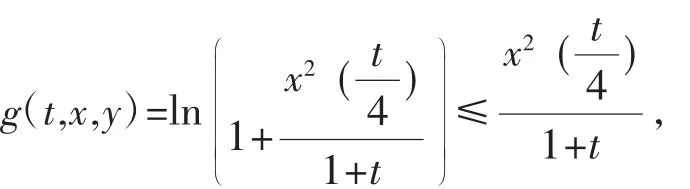
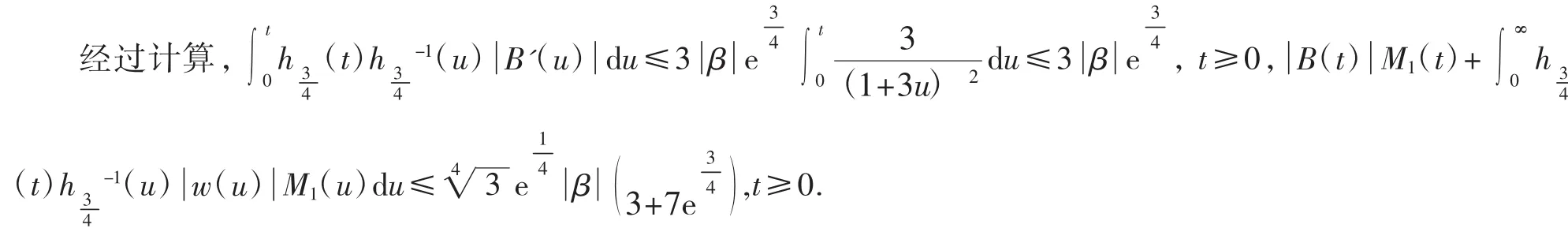
如果：

由（15）和（16）得：

4 结论

本文采用Krasnoselskii不动点定理研究非线性中立型微分方程的h-渐近稳定性，将文献中的线性项进一步推广成，并给出范例加以说明.对于文中的非线性项可推广成更一般的非线性项，只需改变或增加一些条件,依然能证明非线性中立型微分方程的h-渐近稳定性.

［1］Burton T A.Liapunov functionals,fixed points,and stability by Krasnoselskii’s theorem[J].Nonlinear Studies,2002,9(2):181-190.

［2］Burton T A.Stability by fixed point theory for functional differential Equations[M].New York:Dover Publications,2006.

［3］Manuel Pinto,Daniel Sepúlveda.H-asymptotic stability by fixed point in neutral nonlinear differential equations with delay[J].Nonlinear Analysis,2011,74(4)：3926-3933.

［4］Raffoul Y N.Positive periodic solutions in neutral nonlinear differentral equations[J].J Qual Theory Diff Equa，2007（16）：1-10.

［5］Ernest Yankson.Existence of periodic solutions for totally nonlinear neutral differential equations with functional delay[J].Opuscula Mathematica,2012，3(32):617-627.

H-asymptotic Stability by Fixed Point in Nonlinear Neutral Differential Equations with Functional Delay

HUANG Ming-hui
（Department of Basic,Guangzhou Huaxia Technical College,Guangzhou 510935,Guangdong,China）

In this article,it used a variant of Krasnoselskii's fixed point theorem to obtain h-asymptotic stability results about the zero solution of nonlinear neutral differential equations with functional delay.The results promoted the thermo of Pinto and Sepulveda and provided an example that illustrates the results.

h-asymptotic stability;large contraction;nonlinear

0175.14

A

1007-5348（2017）06-0011-05

（责任编辑：邵晓军）

2017-03-16

广东省自然科学基金（2015A030310390）.

黄明辉（1988-），男，广东从化人，广州华夏职业学院基础部讲师，硕士；研究方向：微分动力系统.