具有分布式时滞与一步随机时滞系统的滤波

赵忠义，邹 磊，宋保业

(山东科技大学 电气与自动化工程学院, 山东 青岛 266590)

赵忠义，邹 磊，宋保业

(山东科技大学 电气与自动化工程学院, 山东 青岛 266590)

近年来，由传感器、执行器、控制器与滤波器通过网络构成的网络化系统以其成本低、设计灵活、易于扩展、便于维护等优点受到了越来越多的关注，逐步成为控制界及工业界的研究热点[1-2]。在网络化系统中，被控对象通过网络与控制器、滤波器等部件相连接。由于网络带宽有限等因素的影响，数据在传输过程中会产生时滞现象，并且该现象的发生具有随机性，使得要研究的网络化系统不再是确定性的，而成为随机系统[3-7]。

1 问题描述

考虑一类带有分布式时滞的离散时间系统：

(1)

其中:x(k)∈Rn为状态向量，y(k)∈Rq为输出向量，z(k)∈Rl为待估计的信号，ω(k)∈Rp为能量有界的外部扰动，ψ(k)为x(k)的初值函数，A、Ad、B、C、D、L表示具有适当维数的常数矩阵，常数τj≥0(j=1,2,…,d)。

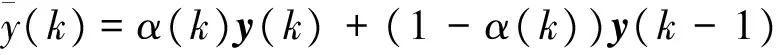
(2)

其中，随机变量α(k)服从Bernoulli分布，即

Prob{α(k)=1}=E{α(k)}=ρ，Prob{α(k)=0}=E{1-α(k)}=1-ρ。

(3)

ρ∈[0,1]为已知的常数。

考虑如下滤波器：

(4)

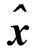
定义：

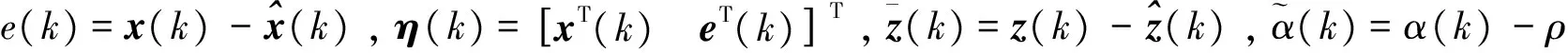
(5)

由式(1)、式(4)可得滤波误差系统模型：

(6)

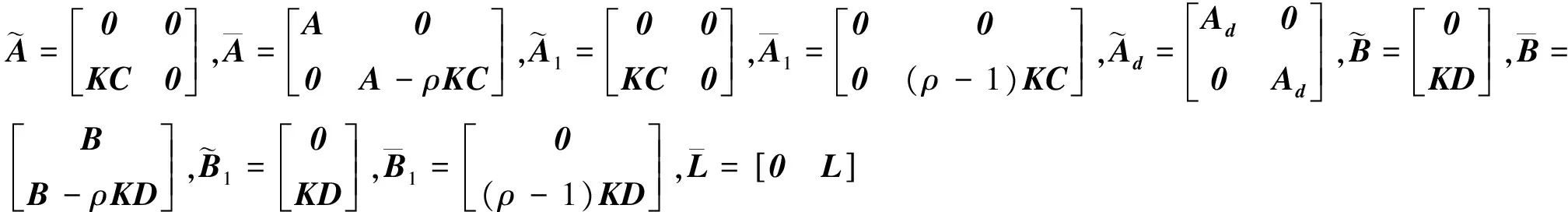
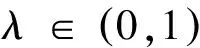
(7)

对任意η(0)∈R2n，k∈Z+成立，则称滤波误差系统(6)是均方指数稳定的。

定义2[9]对于给定的常数γ>0及非零的ω(k)，若滤波误差系统(6)均方指数稳定，且在零初始条件下，

(8)

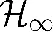
2 主要结果

首先引入需要使用的两个引理。

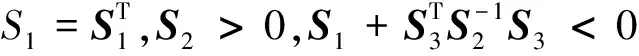
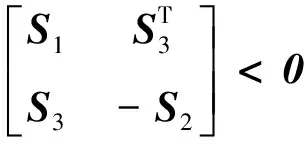
引理2[11]设M为n阶正定矩阵，xi∈Rn，常数ai≥0(i=1,2,…,d)，则有：

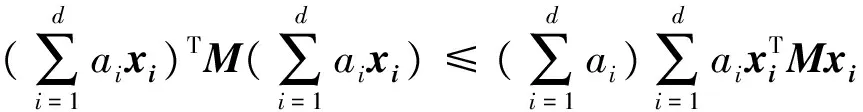
(9)

定理1 给定滤波器参数K及常数γ>0，如果存在矩阵P>0，Q>0，R>0，使得

(10)

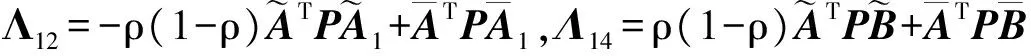
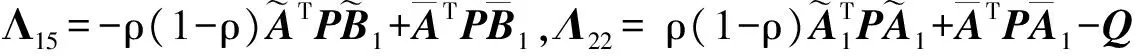
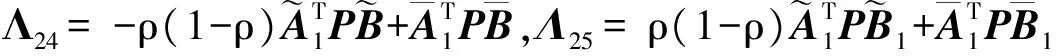
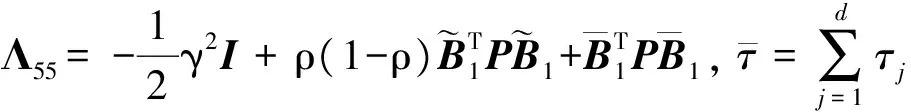
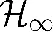
(11)

证明：对滤波误差系统(6)构造李亚普诺夫函数

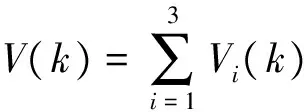
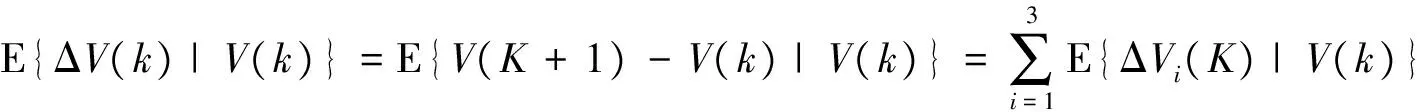
(12)

E{ΔV1(k)|V(k)}=ηT(k)Qη(k)-ηT(k-1)Qη(k-1)。

(13)

根据引理2可得

(14)

E{ΔV3(k)|V(k)}

= E{ηT(k+ 1)Pη(j+ 1)-ηT(k)Pη(k)|V(k)}

(15)

令

(16)

(17)

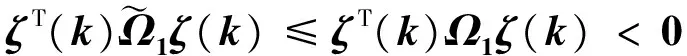
(18)

由文献[3]的定理1可以证明系统均方指数稳定。

(19)

在零初始条件下，考虑如下性能指标：

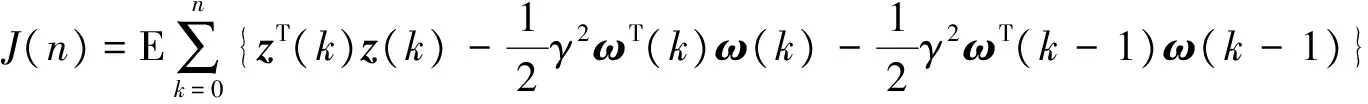
-E{V(n+1)}-E{V(0)}

(20)

根据定理1，由Ω<0可得J(n)<0，又因为

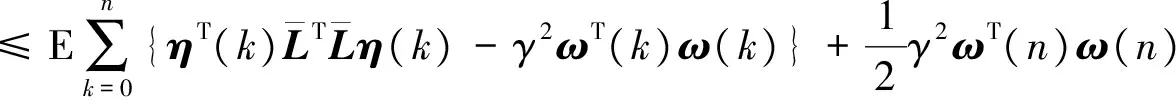
(21)

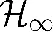
定理2 给定常数γ>0，如果存在矩阵P=diag{P1,P2}>0，Q>0，R>0，Z使得

(22)

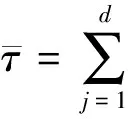
3 仿真算例

考虑具有以下参数的系统：

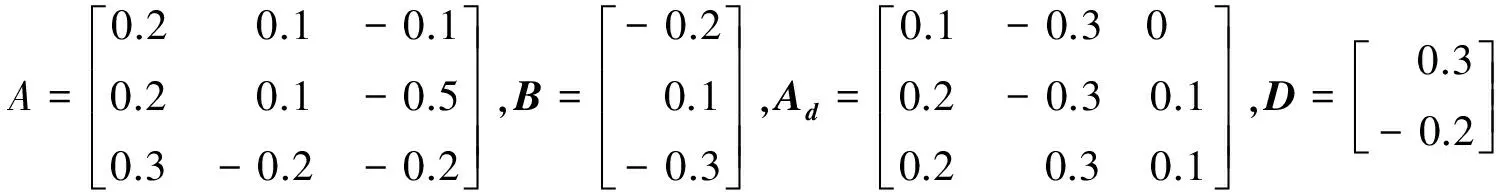
(23)

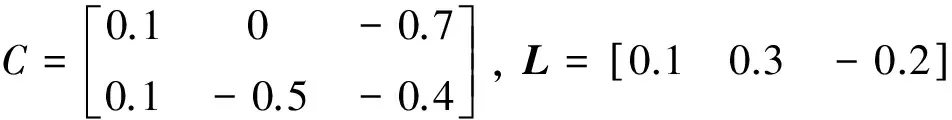
(24)

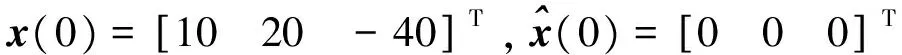
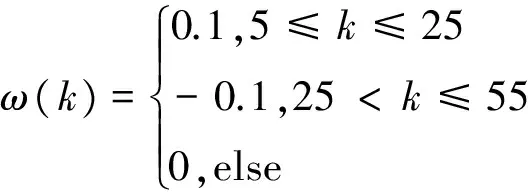
(25)

(26)

图1 z(k)与的状态轨迹Fig.

通过增大时滞d的值，得到当d=5时，定理2给出的线性矩阵不等式已经没有可行解，由此验证了对时滞对于系统的影响的分析。

仿真结果如图1所示：k≥10时，估计值已接近真实值；k≥40时，估计误差达到0。由此验证了滤波误差系统均方稳定。

4 结论

[1]WALSH G C,YE H.Scheduling of networked control systems[J].IEEE Control Systems Magazine,2001,21(1):57-65.

[2]DONG H,WANG Z,GAO H.Robust filtering for a class of nonlinear networked systems with multiple stochastic communication delays and packet dropouts[J].IEEE Transactions on Signal Processing,2010,58(4):1957-1966.

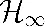
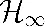
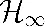
[6]WEI G,WANG Z,SHU H.Robust filtering with stochastic nonlinearities and multiple missing measurements[J].Automatica,2009,45(3):836-841.

[10]BOYD S P,GHAOUI E L,FERON E,et al.Linear matrix inequalities in system and control theory[M].Philadelphia:Society for Industrial and Applied Mathematics,1994.

[11]LIU Y,WANG Z,LIANG J,et al.Synchronization and state estimation for discrete-time complex networks with distributed delays[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B (Cybernetics),2008,38(5):1314-1325.

[15]俞立.鲁棒控制—线性矩阵不等式处理方法[M].北京：清华大学出版社，2002.

(责任编辑：吕海亮)

ZHAO Zhongyi,ZOU Lei,SONG Baoye

(College of Electrical Engineering and Automation, Shandong University ofScience and Technology, Qingdao, Shandong 266590, China)

2017-04-08

中国博士后科学基金项目(2016M600547)；山东省高等学校科研计划项目(J14LN34)

赵忠义(1994—),男，山东泰安人，硕士研究生，从事网络化控制和滤波研究.E-mail:15764246411@163.com 邹 磊(1987—)，男，江西新余人，博士后，研究方向为网络化系统的控制及滤波等，本文通信作者. E-mail:zoulei_cup@gmail.com 宋保业(1982—)，男，山东青岛人，讲师，博士，研究方向为智能控制及其应用.

TP273

A

1672-3767(2017)04-0101-07

10.16452/j.cnki.sdkjzk.2017.04.015