流出系数故障对三容水箱系统的影响

张 丹,刘 洋

(1.山东科技大学 数学与系统科学学院,山东 青岛 266590;2.山东科技大学 电气与自动化工程学院,山东 青岛 266590)

流出系数故障对三容水箱系统的影响

张 丹1,刘 洋2

(1.山东科技大学 数学与系统科学学院,山东 青岛 266590;2.山东科技大学 电气与自动化工程学院,山东 青岛 266590)

研究了三容水箱中流出系数故障对系统稳定性的影响，流出系数的变化直接影响了一步转移矩阵的稳定性，进而影响了系统的整体性能。首先，通过建立三容水箱的模型，得出了系数矩阵与流出系数的关系，然后通过仿真模拟，得到了各个流出系数对系数矩阵特征值的影响的仿真图。最终根据仿真图分析了流出系数故障对三容水箱系统稳定性的影响。

三容水箱系统；流出系数；故障诊断

随着现代科技的发展，故障诊断与容错控制在现代工业中的应用越来越广泛。工业生产中如果出现某些故障，不仅会影响生产进度，而且可能诱发大量安全隐患[1]。在工业过程中，系统的稳定性与安全性非常重要，不仅能保障操作人员的人身安全，也可提高生产效率和经济效益[2]。故障检测技术对系统的输入输出进行监测分析，判断是否有故障发生，是实现故障分离、故障估计和容错控制的必要前提。在过去的十多年里，故障诊断与容错控制技术快速发展，取得了大量研究成果[3]。

三容水箱系统是典型的过程控制实验设备之一，被广泛应用于国内外大学和实验室，它不仅可以作为液位过程控制的实验设备，也可应用于故障诊断研究中[4]。三容水箱是典型的非线性、延时对象，具有很好的代表性，通过对三容水箱系统的稳定性进行研究，可以模拟工业生产过程中对液位、流量参数进行测量、控制，观察其变化特征，从而使三容水箱成为过程控制教学、实验和研究的理想实验平台[5-6]。

流出系数定义为实际流量与理论流量的比值，是三容水箱建模中的一个重要参数，许多研究均围绕这个参数展开[7]。随着工业对流量测量精确度的要求越来越高，对三容水箱流出系数变化影响的研究引起关注，在实际系统中流出系数的标称值与真实值之间存在一定误差。因此，研究流出系数对三容水箱中系数矩阵的影响是非常重要的[8]。

线性系统是最基本的一类动态系统，其研究在于认识和避免线性系统中可能发生的有害运动行为[9]，对其稳定性研究非常重要。三容水箱系统在工作点附近线性化之后，流出系数的变化会直接影响一步转移矩阵的稳定性，进而极大地影响系统性能。

本文针对三容水箱的实验平台，构造其机理模型，该模型物理意义明了、准确度高、适应性强，可为后续分析建立数学基础和保障；并通过流出系数故障对三容水箱系统的影响进行讨论，深入探究这一重要参数在系统动态演化中所起的作用。

1 系统建模

1.1 三容水箱系统建模

对于连续时刻t，用hi代表Ti的液位高度(i=1,3,2)，在h1>h3>h2假设下，由广义的Torricel法则可得如下非线性系统：

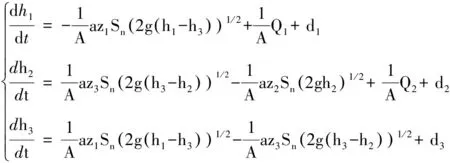
(1)

对i=1,2，3,azi∈(0,1)为水箱Ti的流出系数，di为打水过程中液面波动及其他扰动的等效，m3/s，实验过程中由人工设置；Q1,Q2分别为水泵1和水泵2的进水量，m3/s；H为箱截面积，m2；Sn为连接管道的截面积，m2；g为重力加速度，m/s2。

引入如下变量：

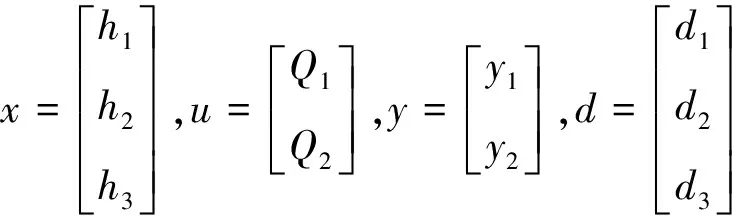
(2)

式中，x∈R3为系统状态，u∈R2为控制输入，y∈R2为测量输出，d∈R3为扰动信号。

系统参数为：

(3)

定义向量为：

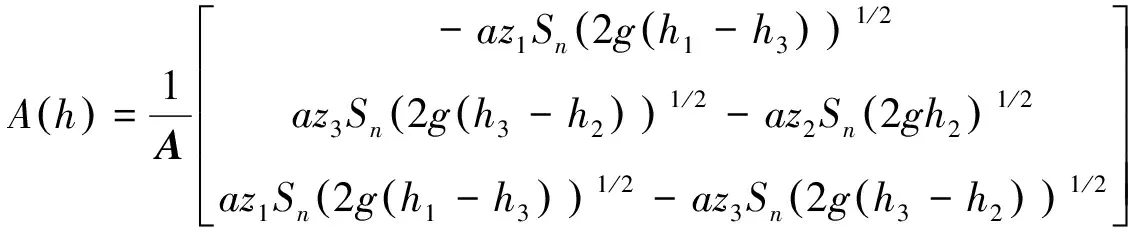
(4)

定义矩阵为：

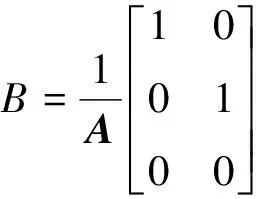
(5)

至此建模完成。

1.2 线性化求解

利用输入Q1=38×10-6m3/s,Q2=18×10-6m3/s，得到系统的稳定工作点为：

h1=0.413 5 m,h2=0.177 7 m,h3=0.295 8 m

以下用泰勒公式对系统在工作点处线性化，将公式：

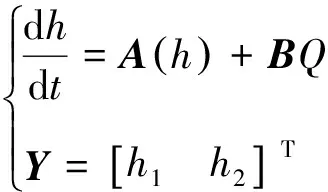
(6)

表示的非线性系统围绕工作点线性化后的线性系统可以表示为：

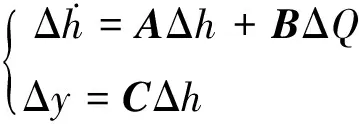
(7)

系数矩阵为：

(8)

根据三容水箱的数学模型，利用泰勒公式的线性化求解，对系数矩阵进行化简与整理，得出未知参量为流出系数az的系数矩阵，因此需要分析流出系数的变化对系数矩阵稳定性的影响，从而得出系数矩阵的稳定范围。接下来，通过仿真验证来研究在不同环境下，不同az的变化对于系数矩阵A的特征值和稳定性的影响。

2 仿真验证

2.1 假设验证

定义在h1>h3>h2前提下，分别通过对az1,az2,az3取值变化来分析系数矩阵A稳定性的影响。

2.1.1 az1对矩阵A的影响变化

把az1看为变量，代入所对应的相关参数值得：

(9)

接下来研究流出系数az1对系数矩阵A稳定性的影响。矩阵A的特征方程为：

=λ3+0.074 2λ2+(1.101 43×10-4az1+9.922×10-5)λ+2.073 69×10-5az1。

(10)

用MATLAB仿真得到图1。可看出随着流出系数取值的变化，各个特征值也随之改变，当流出系数取值越接近于1，一步转移矩阵的特征值离虚轴越来越远，系数矩阵的稳定性也随之变化。

2.1.2 az2对矩阵A的影响变化

通过对az2取值分析，并代入所对应的相关参数值得：

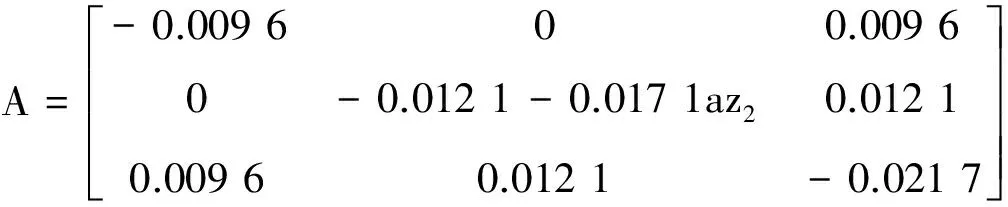
(11)

研究带有未知参量az2的系数矩阵A稳定性，先计算出矩阵A的特征方程为：

=λ3+(0.043 4+0.017 1az2)λ2+(0.031 6+0.017 1az2)λ-0.005 8×10-5+0.198 6×10-5az2。

通过计算可以求得矩阵A带有未知参量az2的特征值和特征向量，并改变未知参量的取值观察其特征值的变化，然后通过特征值的变化范围来观察系数矩阵的稳定性。

对于变量az2进行赋值，找到系数矩阵最稳定时az2的取值点。用MATLAB仿真得到图2。

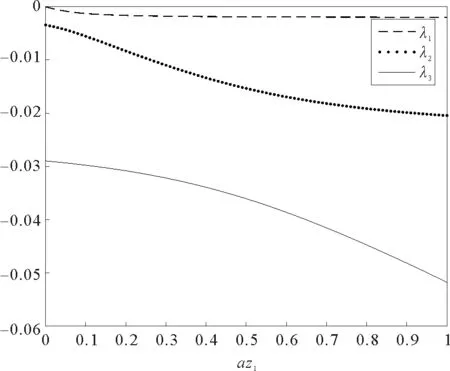
图1 流出系数az1对矩阵A特征值的影响Fig.1 Influence of outflow coefficient az1on the eigenvalues of matrix A

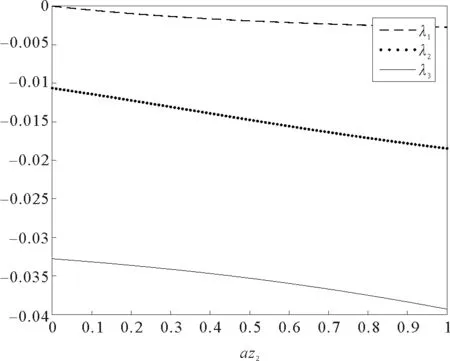
图2 流出系数az2对矩阵A特征值的影响Fig.2 Influence of outflow coefficient az2on the eigenvalues matrix A

通过仿真图可看出，当az2的取值越大时，一步转移矩阵特征值越远离虚轴，系数矩阵越稳定，从而得到流出系数与系数矩阵的稳定性关系。

2.1.3az3对矩阵A的影响变化

定义az3为变量，带入所对应的相关参数值得：

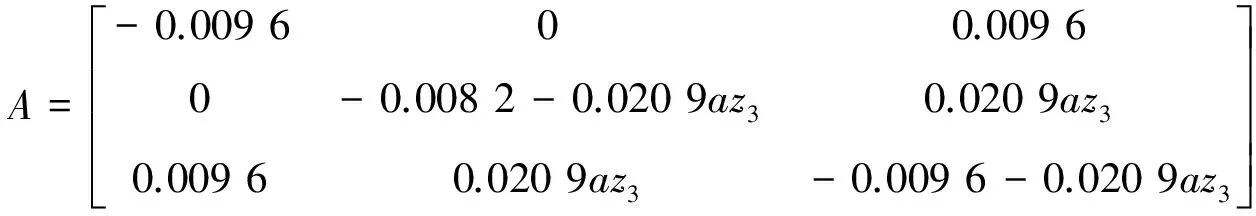
(12)

进而研究流出系数az3对系数矩阵A稳定性的影响。对于矩阵A，其特征方程有

(13)

通过求解矩阵A的特征值和特征向量，并研究流出系数az3的变化，观察系数矩阵的稳定性。用MATLAB来做仿真图，如图3。

图3 流出系数az3对矩阵A特征值的影响Fig.3 Influence of outflow coefficient az3on the eigenvalues of matrix A

根据图3可以看出，对于流出系数az3，当取值越接近于1时，特征值离虚轴越远，系数矩阵也越稳定。

因此，通过三容水箱的系统建模，得出系数矩阵与流出系数的关系式；通过定义三容水箱的3个液位高度，通过3组仿真实验，均得出同一结论：当流出系数的取值越接近于1时，一步转移矩阵特征值离虚轴越远，系数矩阵越稳定。

2.2 对比验证

根据定义的3个液位高度进行3组仿真实验，得出流出系数对三容水箱系统稳定性的影响，接下来通过改变三容水箱系统的稳定工作点，验证以上结论的正确性。因此，在h2>h3>h1条件下，选取一组数据对比验证。根据流出系数az1的取值变化，分析不同液位高度下，流出系数的大小对系数矩阵稳定性的影响。

取得系统的稳定工作点为：h1=0.167 6 m,h2=0.421 5 m,h3=0.285 4 m 。

(14)

由广义的Torricelli法则可得如下非线性系统：

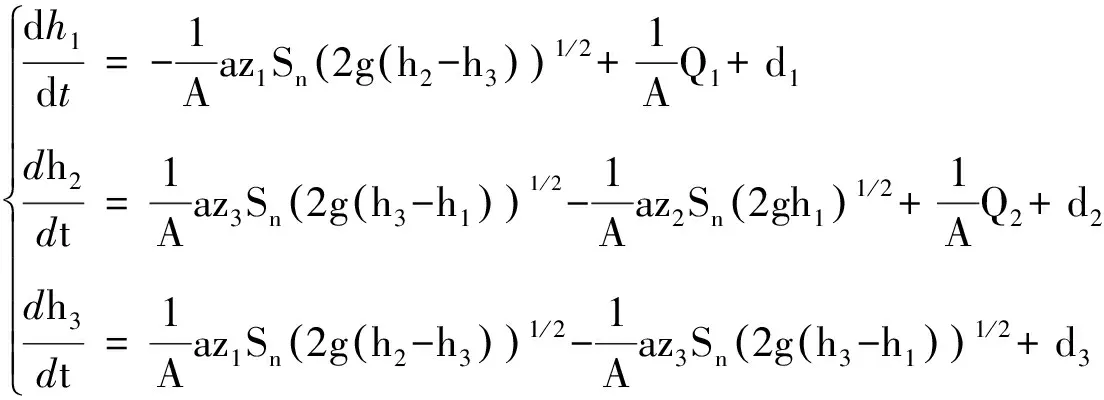
(15)

所对应的系数矩阵为：

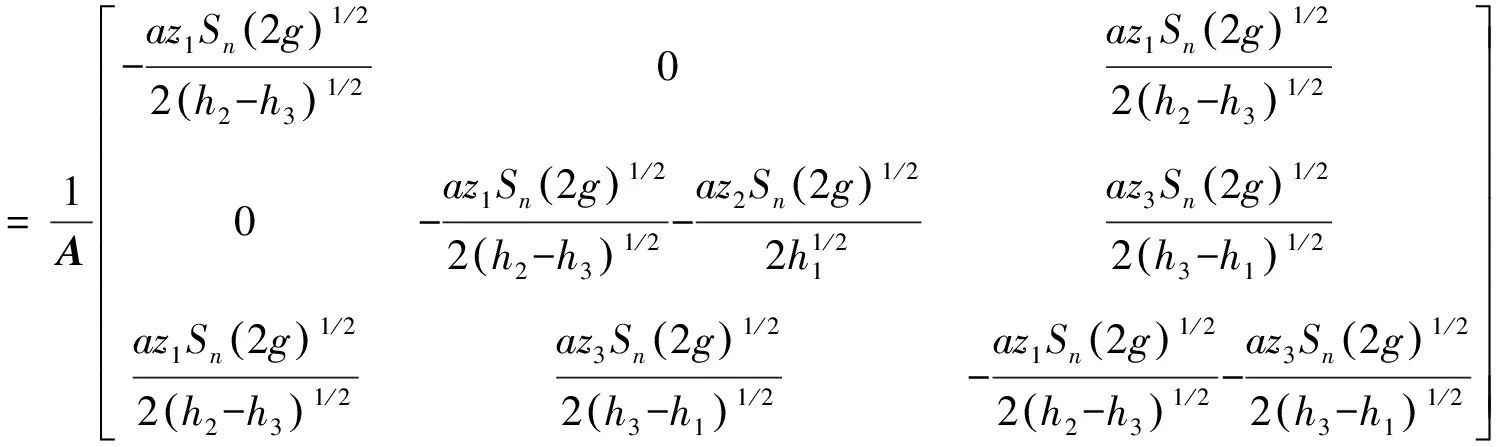
(16)

对于一步转移矩阵A定义az1为变量，代入相应的已知参量值，可得到：

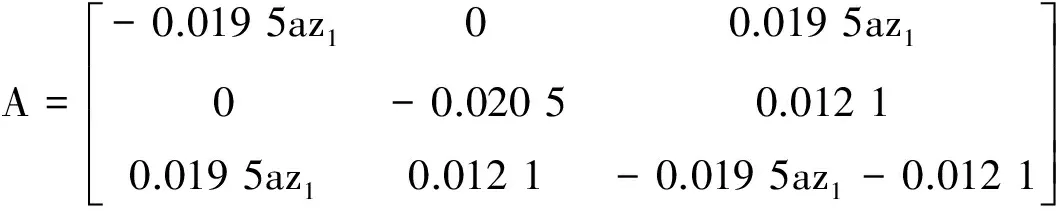
(17)

求矩阵A的特征方程为：

=λ3+(0.039 0az1+0.032 6)λ2+(0.001 0az1+0.000 1)λ+0.019 8×10-4az1。

(18)

用MATLAB计算其特征值和特征向量，并得到仿真图4。

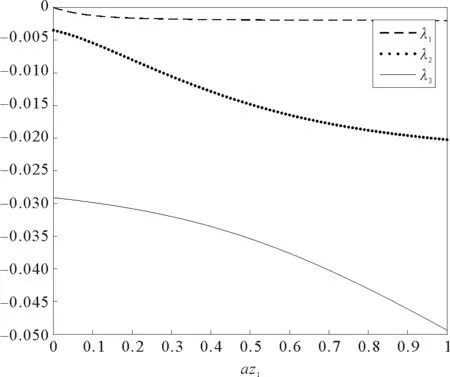
图4 流出系数az1对矩阵A特征值的影响Fig.4 Influence of outflow coefficient az1on the eigenvalues of matrix A

与图1对比可得出，改变系统工作的稳定点并不影响流出系数对系统稳定性的影响，随着流出系数取值的不断增大，系数矩阵也越来越稳定。

对于流出系数az2,az3也有相同的结论，在此，不一一列举。

因此，通过改变系统的稳定点进行两组数据对比验证，得出同一结论：流出系数影响系数矩阵的稳定性，随着流出系数的不断增大，一步转移矩阵特征值离虚轴越来越远，系数矩阵越来越稳定。

3 结论

本文利用三容水箱的系统建模得到一个关于流出系数为未知参量的系数矩阵，分析流出系数对三容水箱稳定性的影响。通过对流出系数的取值变化来观察系数矩阵稳定性的变化范围，并且运用MATLAB仿真分析各个流出系数对系数矩阵稳定性的影响，然后通过改变三容水箱的液位高度来对比验证此实验结果的准确性，最后由多组仿真实验得到了同一结论，随着流出系数取值的增大系数矩阵越稳定。

[1]周东华，刘洋，何潇.闭环系统故障诊断技术综述[J].自动化学报，2013,39(11):1933-1943. ZHOU Donghua,LIU Yang,HE Xiao.Review on fault diagnosis techniques for closed-loop systems[J].Acta Automatica Sinica,2013,39(11):1933-1943.

[2]王德军，李元春.故障诊断与容错控制方法研究[D].长春：吉林大学，2004.

[3]周东华，叶银忠.现代故障诊断与容错控制[M].北京：清华大学出版社，2000.

[4]徐国旺.三容水箱系统故障诊断算法研究[D].哈尔滨：哈尔滨工业大学，2008.

[5]李智，赵子先.基于模糊PID的三容水箱液位控制[D].呼和浩特：内蒙古大学，2007.

[6]赵科，王生铁，张计科.三容水箱的机理建模[J].控制工程，2006,13(6)：521-524. ZHAO Ke,WANG Shengtie,ZHANG Jike.Mechanism modeling of three-tank[J].Control Engineering of China,2006,13 (6):521-524.

[7]徐英，吴经纬，杨会峰，等.内锥流量计流出系数预测方法研究[J].计算力学学报，2009,26(5)：727-733. XU Ying,WU Jingwei,YANG Huifeng,et al.Study on prediction method of outflow coefficient of inner cone flowmeter[J].Chinese Journal of Computational Mechanics,2009,26(5):727-733.

[8]翟秀真，童复来，高立忠.孔板流出系数研究[J].计量技术，1997(6)：37-39. ZHAI Xiuzhen,TONG Fulai,GAO Lizhong.Study on outflow coefficient of orifice plate[J].Measurement Technique,1997 (6):37-39.

[9]郑大钟.线性系统理论[M].北京：清华大学出版社，2002.

(责任编辑：高丽华)

Influences of Outflow Coefficient Failure on Three-tank Systems

ZHANG Dan1,LIU Yang2

(1.College of Mathematics and Systems Science,Shandong University of Science andTechnology,Qingdao,Shandong 266590,China;2.College of Electrical Engineering and Automation,Shandong University of Science andTechnology,Qingdao,Shandong 266590,China)

In this paper, the influences of outflow coefficient failure on the stability of three-tank systems were studied. The changes of the outflow coefficients would directly affect the stability of the one-step transmission matrix and in turn the system performance. First, the relationship between the coefficient matrix and the outflow coefficients was obtained by establishing the model of the three-tank system. Then the simulation figures of the influences of each outflow coefficient on the eigenvalue of the coefficient matrix were obtained. Finally, the influences of the outflow coefficients on the stability of the three-tank system were analyzed based on the simulation results.

three-tank systems (TTSs);outflow coefficient;fault diagnosis

2017-04-14

中国博士后科学基金项目(2016M600546)；青岛市博士后研究人员应用研究项目(2016112)；山东科技大学研究生科技创新项目(SDKDYC170354)

张 丹(1993—)，女，山东寿光人，硕士研究生，主要从事故障检测与诊断方面的研究.E-mail:zdcyndi@163.com 刘 洋(1988—)，男，辽宁海城人，博士后，主要从事最优滤波、闭环系统、故障检测与诊断的研究，本文通信作者.E-mail:lianinliyan@163.com

TQ35

A

1672-3767(2017)04-0066-07

10.16452/j.cnki.sdkjzk.2017.04.010