基于粒子群优化算法的分数阶PID控制器设计
赵华东,宋保业,张建胜,许 琳
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
基于粒子群优化算法的分数阶PID控制器设计
赵华东,宋保业,张建胜,许 琳
(山东科技大学 电气与自动化工程学院,山东 青岛 266590)
分数阶PID控制器具有可变的微分和积分阶次,通过调整控制器参数可以获得更好的控制性能。本文基于粒子群优化算法设计分数阶PID控制器。首先介绍分数阶PID和粒子群优化算法,然后给出分数阶PID控制系统结构、分数阶微积分算子的近似算法和分数阶PID控制器设计的仿真流程,最后通过MATLAB/Simulink对算例进行控制器设计仿真。仿真结果表明,通过粒子群寻优能够获得满意的分数阶PID控制器参数,满足对控制性能的要求。
粒子群优化;分数阶控制器;比例-积分-微分
PID(比例-积分-微分, proportional-integral-derivative)控制器是目前工业生产中应用最广泛的控制器,而近年来发展起来的分数阶PID控制器在经典PID控制器基础上增加了两个可调参数,从而可以在原有PID控制器基础上进一步优化控制性能、提高控制品质,其适用对象包括分数阶系统和整数阶系统[1]。
近年来,大量的启发式智能优化算法被用于PID控制器参数整定和分数阶PID控制器设计,如文献[2]提出基于改进遗传算法的分数阶PID控制器,显著优化系统性能并提高了系统鲁棒性。文献[3]提出一种基于改进蜂群算法的分数阶PID控制器设计方法,新算法能够扩大搜索范围避免陷入局部极小点,从而获得最优的控制器参数。此外,禁忌搜索算法[4]、差分进化算法[5]、粒子群优化算法[6]等也被用于分数阶PID控制器设计。
本文基于粒子群优化(particle swarm optimization,PSO)算法给出一种分数阶PID控制器设计的MATLAB/Simulink仿真方法。首先介绍分数阶PID控制器和粒子群优化算法,然后给出基于粒子群优化算法的分数阶PID控制器设计方法和仿真流程,最后通过算例比较验证设计结果的优越性。
1 分数阶PID控制器
分数阶微积分是经典微积分的一般化,其微积分阶次从整数扩展到非整数,包括任意实数甚至复数[7]。分数阶微积分的定义有多种形式,其中Grunwald-Letnikov(GL)分数阶微积分定义和Riemann-Liouville(RL)分数阶微积分定义是最常用的两种,并且可以证明在实际物理系统和工程应用中,两者是完全等效的[8]。对连续可导函数f(t)的r阶Grunwald-Letnikov微积分定义如下[9]:

(1)

(2)
其中,n-1 (3) 其中,L{·}表示拉普拉斯变换,s为拉普拉斯算子。 分数阶动态系统可用如下的分数阶微分方程描述: anDαny(t)+an-1Dαn-1y(t)+……+a0Dα0y(t) =bmDβmu(t)+bm-1Dβm-1u(t)+…+b0Dβ0u(t), (4) (5) 图1 分数阶控制系统框图Fig.1 Block diagram of fractional-order control system 单输入单输出分数阶控制系统的框图如图1所示。其中,r为给定值,y为被控对象输出值,e为两者的偏差,分数阶PID控制器即根据偏差e调整控制器输出u。分数阶PID控制器的微分方程表达式为: u(t)=Kpe(t)+KiD-αe(t)+KdDβe(t), (6) 其相应的控制器传递函数为: (7) 其中,Kp、Ki、Kd分别为比例、积分和微分增益,α和β分别为积分和微分阶数。当α和β为1时,分数阶PID控制器退化为经典的整数PID控制器。与整数阶PID控制器相比,分数阶PID控制器中积分和微分的阶次可不为1,从而为控制器设计增加了两个可调参数,使得分数阶PID控制器与整数阶PID控制器相比达到更好的控制性能指标。 粒子群优化算法是由Kennedy和Eberhart提出的一种模拟鸟群或鱼群群体行为的启发式智能优化算法[10],目前已经被广泛地应用于各类优化问题的求解。粒子群优化算法定义了一组与优化问题相关的粒子,每一个粒子是待优化问题的一个可行解,其维数与优化问题可行解的维数相同。粒子群优化算法根据各个粒子的历史最优解和粒子群中的全局最优解迭代更新每一个粒子的飞行速度,并进而更新粒子位置,最终得到优化问题的最优解。粒子群优化算法的速度更新方程和位置更新方程如下: vi(k+1)=wvi(k)+c1r1(pi(k)-xi(k))+c2r2(pg(k)-xg(k)); (8) xi(k+1)=xi(k)+vi(k+1) 。 (9) 其中,w为惯性权系数,vi(k)和xi(k)分别为粒子i在第k代的速度和位置,pi(k)和pg(k)分别为粒子i的历史最优位置和当前代粒子群中的全局最优位置,常数c1和c2称为加速系数,r1和r2为[0,1]中均匀分布的随机数。 目前,众多学者提出了一系列改进的PSO算法。如Shi等[11]提出了惯性权系数线性降低的PSO-LDIW算法,其惯性权系数的计算方法为 (10)其中,kmax为最大迭代次数。Ratnaweera等[12]提出了具有时变加速系数的PSO-TVAC算法,其加速系数计算如下 (11) (12) Clerk[13]为提高算法的搜索性能提出了具有压缩因子的PSO-CK算法等。此外,除了对PSO算法中的参数选择提出改进方法之外,结合多种辅助操作的混杂PSO算法也是学者们关注的研究方向[14-16]。 本文使用MATLAB/Simulink仿真,基于粒子群优化算法设计分数阶PID控制器。由于MATLAB目前尚没有正式推出面向分数阶系统仿真的工具箱,因此分数阶PID控制器首先近似为整数阶系统,然后可按照整数阶系统搭建仿真环境,系统仿真框图如图2所示。 图2 分数阶PID控制系统Fig.2 Fractional-order PID control system 在仿真过程中,本文使用Oustaloup 近似化方法对分数阶PID控制器中的微积分算子进行近似。设待近似的微积分算子为sγ,拟合频率段为(ωb,ωh),则可以构造出一个近似sγ的频域滤波器如下[9]: (13) (14) (15) (16) 本文的粒子群优化算法中的粒子为5维,各维分别为Kp、Ki、Kd、α、β。优化过程中最大迭代次数为100,种群规模为20,按照式(10)~(12)计算惯性权系数和加速系数,分数阶PID控制器设计的仿真流程如图3所示。 为验证本文的分数阶PID控制器设计方法的有效性,以下使用文献[17]中的两个典型算例,采用平方偏差积分(square deviation integral, ISE)、时间平方偏差积分(time squared deviation integral, ITSE)、绝对偏差积分(absolute deviation integral, IAE)和时间绝对偏差积分(time absolute deviation integral,ITAE)4种性能指标设计分数阶PID控制器并进行比较。 图3 分数阶PID控制器设计仿真流程Fig.3 Simulation flowchart of fractional-order PID controller design 例1 高阶被控对象的传递函数为: (17) 文献[17]中给出的控制器为: C(s)=0.741 3(1+0.186 9/s1.310 6) 。 (18) 根据文献[18]基于误差的最优控制器设计程序,对例1进行整数阶PID参数寻优,得到的控制器为: (19) 本文采用4种性能指标(ITSE、ITAE、ISE、IAE)得到的分数阶PID控制器参数如表1所示,图4给出了各控制器的阶跃响应,表2给出了相应控制器的性能指标。 由以上仿真结果可见,采用本文给出的参数优化方法所得到的系统阶跃响应的超调量均不超过10%,远远小于采用文献[17]和[18]方法得到的超调量;同时,除基于ISE指标的调节时间略大外,其余控制器性能指标均优于文献[17]和[18]中的设计方法;这说明本文给出的分数阶PID控制器设计方法比现有方法具有更好的性能。 表1 例1分数阶PID控制器参数Tab.1 Parameters of fractional-order PID controllers of exampe 1 图4 例1各控制器的阶跃响应Fig.4 Step response of controllers in Example 1表2 例1各控制器的性能指标Tab.2 Performance indexes of controllers in Exampe 1 超调量M/%调节时间ts/s峰值时间tp/s上升时间tr/sITSE7.46.7895.8124.593ITAE1.66.7168.4687.575ISE9.811.096.4625.024IAE3.95.3026.9685.832文献[17]22.427.4813.57.958文献[18]34.910.056.9664.856 例2 带时滞被控对象的传递函数为: (20) 文献[17]中给出的控制器为: (21) 根据文献[18]中基于误差的最优控制器设计程序,对例2进行整数阶PID参数寻优,得到的控制器为: (22) 本文采用四种性能指标(ITSE、ITAE、ISE、IAE)得到的分数阶PID控制器参数如表3所示,图5给出了各控制器的阶跃响应,表4给出了相应控制器的性能指标。由以上仿真结果可见,对含有时滞的被控对象,采用本文给出的参数优化方法能够克服文献[17]和[18]中方法的缺陷,所得到的系统阶跃响应具有更优越的性能。 表3 例2分数阶PID控制器参数Tab.3 Parameters of fractional-order PID controllers of Example 2 图5 例2各控制器的阶跃响应Fig.5 Step response of controllers in Example 2表4 例2各控制器的性能指标Tab.4 Performance indexes of controllers in Example 2 超调量M/%调节时间ts/s峰值时间tp/s上升时间tr/sITSE2.13.3214.1653.702ITAE2.43.4658.5113.938ISE33.5096.4294.247IAE2.63.3024.2913.646文献[17]45.233.9710.826.563文献[18]2912.855.1923.873 从仿真结果来看,本文给出的基于粒子群优化算法的分数阶PID控制器设计方法在4种性能指标下均能够得到较好的控制器参数,阶跃响应具有响应速度快、超调量小、稳定时间短的特点,与文献[17]及文献[18]中的设计方法相比能够实现更好的控制性能。 给出了一种基于粒子群优化算法的分数阶PID控制器设计方法,获得的控制器参数能够实现更好的控制性能,并对两个算例通过MATLAB/Simulink仿真验证了设计方法的有效性。本文可作为基于智能优化方法的分数阶PID控制器设计的一般框架,通过修改所使用的智能优化方法,可验证新算法性能并进行比较。在此基础上,将进一步研究自适应的分数阶PID控制器设计方法及数字分数阶PID控制器设计及其应用等。参考文献: [1]CHEN Y Q,PETRAS I,XUE D.Fractional order control:A tutorial[C]//American Control Conference,Missouri:IEEE Press,2009:1397-1441. [2]陈超波,胡莉,马颖,等.一种改进式遗传算法优化分数阶PID控制器[J].西安工业大学学报,2016,36(6):510-516. CHEN Chaobo,HU Li,MA Ying,et al.Improved genetic algorithm for optimal fractional-order PID controller[J].Journal of Xi’an Institute of Technology,2016,36(6):510-516. [3]ZHANG D L,TANG Y G,GUAN X P.Optimum design of fractional order PID controller for an AVR system using an improved artificial bee colony algorithm[J].Acta Automatica Sinica,2014,40(5):973-980. [4]ATES A,YEROGLU C.Optimal fractional order PID design via Tabu Search based algorithm[J].ISA Transactions,2016,60:109-118. [5]MOHARAM A,EL-HOSSEINI M A,ALI H A.Design of optimal PID controller using hybrid differential evolution and particle swarm optimization with an aging leading and challengers[M].North-holland:Elsevier Science Publisher B.V,2016,38:727-737. [6]LIU X.Optimization design on fractional order PID controller based on adaptive particle swarm optimization algorithm[J].Nonlinear Dynamics,2016,84(1):379-386. [7]CHEN Y Q,VINAGRE B M.A new IIR-type digital fractional order differentiator[J].Signal Processing,2003,83(11):2359-2365. [8]VINAGRE B M,PODLUBNY I,HERNANDEZ A,et al.Some approximations of fractional order operators used in control theory and applications[J].Fractional Calculus & Applied Analysis,2000,3(3):231-248. [9]MONJE C A,CHEN Y Q,VINAGRE B M,et al.Fractional-order systems and controls[M].London:Springer Press,2010. [10]KENNEDY J,EBERHART R.Particle swarm optimization[C]//IEEE International Conference on Neural Networks,Perth:IEEE Press,2002,4:1942-1948. [11]SHI Y,EBERHART R.Modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation Proceeding,Alaska:IEEE Press,1998:69-73. [12]RATNAWEERA A,HALGAMUGE S K,WATSON H C.Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients[J].IEEE Transactions on Evolutionary Computation,2004,8:240-255. [13]CLERC M,KENNEDY J.The particle swarm:Explosion,stability,and convergence in a multi-dimensional complex space[J].IEEE Transactions on Evolutionary Computation,2002,6(1):58-73. [14]ANDREWS P S.An investigation into mutation operators for particle swarm optimization[C]//Proceedings of IEEE Congress on Evolutionary Computation,Vancourer:IEEE Press,2006:1044-1045. [15]MENDES R,KENNEDY J,NEVES J.The fully informed particle swarm:Simpler,maybe better[J].IEEE Transactions on Evolutionary Computation,2004,8(3):204-210. [16]ZHANG W J,XIE X F.DEPSO:Hybrid particle swarm with differential evolution operator[C]// Proceedings of IEEE International Conference on Systems,Man,and Cybernetics,Washington:IEEE Press,2004:997-1006. [17]王春阳,李明秋,姜淑华,等.分数阶控制系统设计[M].北京:国防工业出版社,2014. [18]薛定宇,陈阳泉.控制数学问题的MATLAB求解[M].北京:清华大学出版社,2007. (责任编辑:高丽华) Fractional-order PID Controller Design Based on PSO Algorithm ZHAO Huadong,SONG Baoye,ZHANG Jiansheng,XU Lin (College of Electrical Engineering and Automation,Shandong University ofScience and Technology,Qingdao,Shandong 266590,China) The performances of the fractional-order PID controller could be advanced by adjusting two of the variable parameters, i.e. differential order and integral order. This paper is concerned with the design of fractional-order PID controller based on particle swarm optimization. Firstly, the fractional-order PID controller and particle swarm optimization were introduced respectively. Then the structure of the fractional-order PID controller, the approximation algorithm of the fractional-order differ-integral operator, and the simulation flowchart of the fractional-order PID controller design were presented. In the end, the controller design was simulated for the examples by MATLAB/Simulink. The simulation results show that with particle swarm optimization, the satisfying fractional-order PID controller parameter could be obtained to achieve better control performances. particle swarm optimization;fractional-order controller;PID(proportional-integral-derivative) 2017-03-22 山东省高等学校科技计划项目(J14LN34) 赵华东(1991—),男,山东泰安人,硕士研究生,主要从事分数阶控制理论与应用的研究. 宋保业(1982—),男,山东青岛人,博士,讲师,主要从事智能优化算法、移动机器人控制的研究,本文通信作者.E-mail:songbaoye@gmail.com TP273 A 1672-3767(2017)04-0060-06 10.16452/j.cnki.sdkjzk.2017.04.009

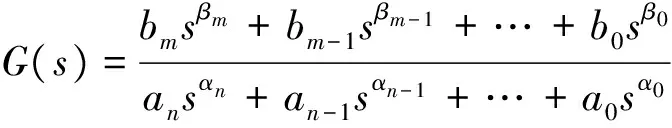


2 粒子群优化算法



3 分数阶PID控制器设计



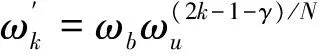













4 结论

