高校学生成绩及教师教学效果SAS统计分析
董小刚, 佟知真, 王纯杰, 李纯净, 张倩倩
(长春工业大学 基础科学学院, 吉林 长春 130012)
高校学生成绩及教师教学效果SAS统计分析
董小刚, 佟知真, 王纯杰*, 李纯净, 张倩倩
(长春工业大学 基础科学学院, 吉林 长春 130012)
以某高校同一学期不同专业学生期末考试成绩作为参考数据,利用多元统计方法进行分析,使用SAS宏程序对学生成绩进行批量处理并对教师教学效果进行评价。
主成分分析; 因子分析; 聚类分析; 典型相关分析; SAS
0 引 言
高等教育规模迅速扩大,使我们在较短时间内迅速提升了我国人力资源的开发水平,推动经济社会的持续快速发展,也带动了综合国力与国际竞争力的持续提高,使我国在未来国际的科技、教育与人才竞争中抢占了有利位置。满足了广大人民群众想要接受到好的教育的迫切愿望,有力地促进了教育的公平公正。
就目前的高校管理来看,特别是对于学生的考试试卷的管理工作中,普遍都存在着不能对试卷成绩数据合理分析与利用的问题[1]。简而言之,考试本身是一种检验教学效果与质量的重要方法,而成绩所能反应出来的信息不仅仅是显示在简单的层面上,需要对它进行更深入的理性分析,找到各方面的成效与得失以及影响学生成绩的相关因素。帮助教师及时地发现教学中存在的一些问题及薄弱环节,使教师可以及时地调整教学方案与内容,更好地指导教师在教学中的工作。
1 模型介绍
1.1 主成分分析法[2]
主成分分析是数学上对数据降维的一种方法。其基本思想是设法将原来众多的具有一定相关性的指标x1,x2,…,xp(p个指标)重新组合成一组较少个数的互不相关的综合指标Fm来代替原来的指标。
主成分分析的具体步骤如下:
1)计算相关系数矩阵;
2)求出相关系数矩阵的特征值以及相应的正交化单位特征向量;
3)选择主成分;
4)计算主成分得分。
1.2 因子分析法
因子分析法就是从研究变量内部相关的依赖关系出发,把一些具有错综复杂关系的变量归结为少数几个综合因子的一种多变量统计分析方法。这样可以对原始的数据进行分类归并,将相关比较密切的变量分别归类,归纳出多个综合性指标,这些综合指标互不相关,即它们所综合的信息互相不重叠。这些综合指标就成为因子或公共因子。
因子分析法的基本思想是将观测变量进行分类,将相关性较高,即联系比较紧密的分在同一类中,而不同类变量之间的相关性则较低,那么每一类变量实际上就代表了一个基本结构,即公共因子。对于所研究的问题就是试图用最少个数不可测的所谓公共因子的线性函数与特殊因子之和来描述原来观测的每一分量。这样能相对容易地以较少的几个因子反映原资料的大部分信息,从而达到浓缩数据,以小见大,抓住问题本质和核心的目的。
因子分析法的核心是对若干个综合指标进行因子分析并提取公共因子,再以每个因子的方差贡献率作为权数与该因子的得分乘数之和构造得分函数。因子分析法的数学表示为:X=AF+B,即:
模型中,X=(x1,x2,x3,…,xp)是可观测随机向量,即原始观测变量。
F=(f1,f2,…,fk)是X=(x1,x2,…,xp)的公共因子,即各个原观测变量的表达式中共同出现的因子,是相互独立的、不可观测的理论变量。B=(β1,β2,…,βp)是X=(x1,x2,…,xp)的特殊因子,是不能被前k个公共因子包含的部分,这种因子也是不可观测的。各特殊因子之间以及特殊因子与所有公共因子之间都是相互独立的。
1.3 聚类分析[3]
聚类分析方法是按样品(或变量)的数据特征把相似的样品或(变量)倾向于分在同一类中,把不相似的样品(或变量)倾向于分在不同类中。聚类分析根据分类对象不同分为Q型和R型聚类分析。距离和相似系数这两个概念反映了样品(或变量)之间的相似程度。相似程度越高,一般两个样品之间的距离就越小。系统聚类法是最常用的一种聚类方法,常用的系统聚类法有最短距离法、最长距离法、中间距离法、类平均法、重心法、离差平方和法、可变法、可变类平均法等。在许多应用中,类平均法和离差平方和法的聚类效果相对较好。
1.4 典型相关分析
典型相关分析(Canonical Calcorrelation Analysis)就是利用综合变量对之间的相关关系来反映两组指标之间的整体相关性的多元统计分析方法。它的基本原理是:为了从总体上把握两组指标之间的相关关系,分别在两组变量中提取有代表性的两个综合变量U1和V1(分别为两个变量组中各变量的线性组合),利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性。
2 实证分析
2.1 数据及变量情况
文中数据来源为某高校2014级学生2014-2015学年第一学期期末考试成绩。数据真实可靠,其中有54 077个观测数据和18个变量。
2.2 教师教学效果分析
文中以数学老师为例进行分析。对原始数据进行处理,其中x1~x12分别代表平均值、中位数、最高分、最低分、90分以上人数、80~90分人数、70~80分人数、60~70分人数、40~60分人数、40分以下人数、平均课时数及所教学生人数。
2.2.1 主成分分析
对经过插补处理后的数据标准化[4-5],之后对数据进行主成分分析。SAS程序如下:
proc princomp data=work.b
out=out1 outstat=stat1 prefix=z; /*对数据进行主成分分析*/
var x1-x12;
run;
proc print data=out1;
title 'outpur:out1';
run;
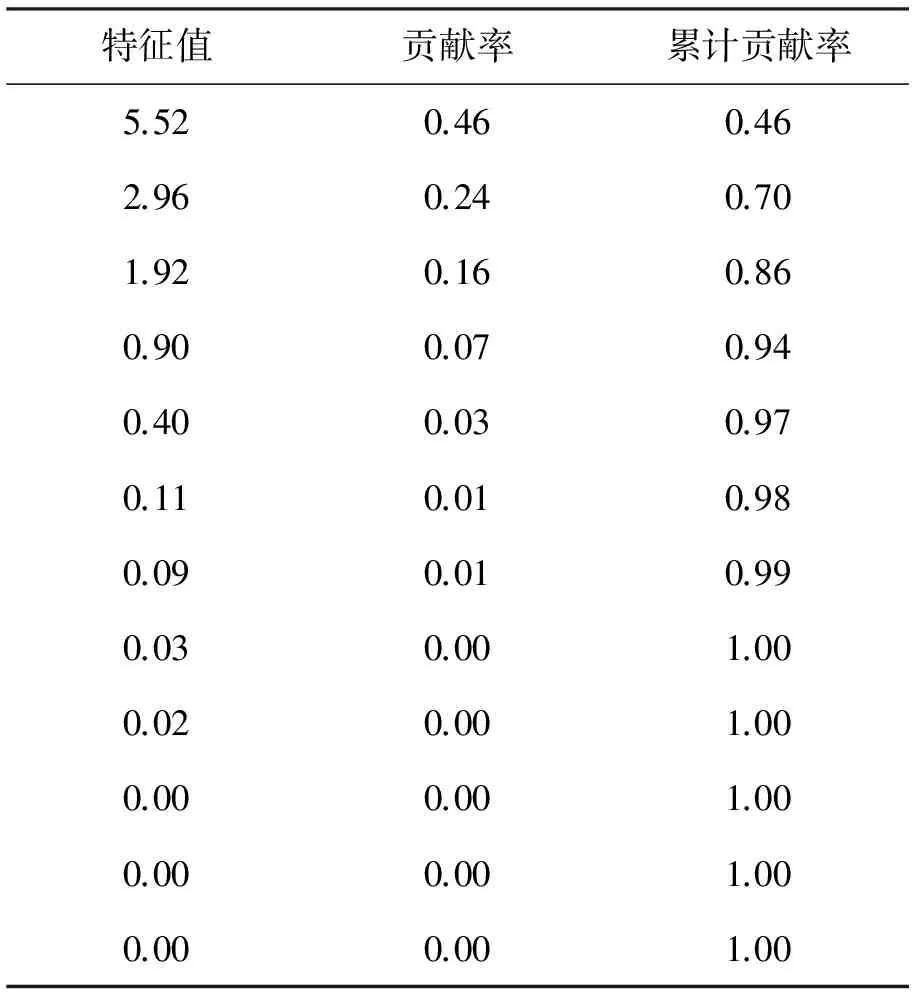
表1 特征值、贡献率、累计贡献率
由累计贡献率可知,只需要取前3个主成分即可。通过观察可知第一主成分中各个变量的系数都为正值,且大小相差不多,我们认为第一主成分值代表了对全部变量的一个综合信息的呈现。其中,x6得分最多,说明该教师所教学生综合成绩最好。主成分分析方法和计算方法如下:
第一主成分:
z1= 0.25x1+0.27x2+0.33x3+0.11x4+
0.39x5+0.4x6+0.3x7+0.15x8+
0.23x9+0.18x10+0.24x11+0.38x12
第二主成分:
z2= -0.458x1-0.425 3x2-0.214x3-
0.151 4x4-0.066x5-0.053 2x6+
0.200 7x7+0.481 1x8+0.146x9+
0.411 4x10+0.163x11+0.210 6x12
第二主成分的大小则主要取决于x1、x2、x8和x10,它们分别为平均值、中位数、60~70分成绩的人数和成绩在40分以下的人数。并且前两个变量的系数为负值,当平均值及中位数越高时,第二主成分的值相对越低,而60~70分与40分以下的人数越多,第二主成分值越高,我们可以就此理解为这是一个负向相关的主成分,即平均成绩越低、低分人数越多时,该名教师的第二主成分值越高。
第三主成分:
z3= -0.021 4x1-0.131 7x2-0.314x3+
0.564 5x4+0.139 4x5+0.154x6+
0.002 8x7+0.247 2x8+0.239 2x9-
0.312 2x10-0.533 3x11+0.145 7x12
第三主成分的大小通过观察可知主要取决于x3、x4、x10和x11,它们分别为最高分、最低分、40分以下人数和平均课时数。当最高分越低而最低分越高时,第三主成分越高,这可以理解为该名教师所教学生的分数差距较少。40分以下人数越少,第三主成分分数越多这一点也可体现出当学生成绩主要分布于中等、学生高分和低分差距越不明显,第三主成分得分越高,则可以将第三主成分看作是表明学生成绩均匀程度的一个主成分。
在第一主成分中,得分越高说明该教师所教学生综合成绩越好,第二主成分得分越高说明该教师所教学生平均成绩低,低分学生多;第三主成分得分越高说明该教师的学生成绩水平越接近,班级总体成绩越均匀。
2.2.2 因子分析
对标准化后的数学教师信息再进行因子分析。文中使用的因子旋转方法[6]是最大方差正交旋转法。SAS程序如下:
proc factor data=b1 rotate=varimax reorder SCORE OUTSTAT=OUTF; /*进行因子分析*/
var x1-x12;
run;
proc score data=b1 score = outf out= outs;
run;
proc sort data=outs;
by descending Factor1 ;run;
proc print data=outs;run;

表2 因子载荷表
旋转后的因子载荷在通过最大方差正交旋转后,得到了12个指标在3个因子上的新的因子载荷。通过观察可以看出,因子F1支配的指标有x5、x6、x7、x8、x9和x12,它们代表的是各分数段人数和总人数,我们将它理解成成绩分布因子,因子F2支配的指标是x1、x2和x3,它代表的是平均成绩因子;因子F3支配的指标是x4、x10和x11。
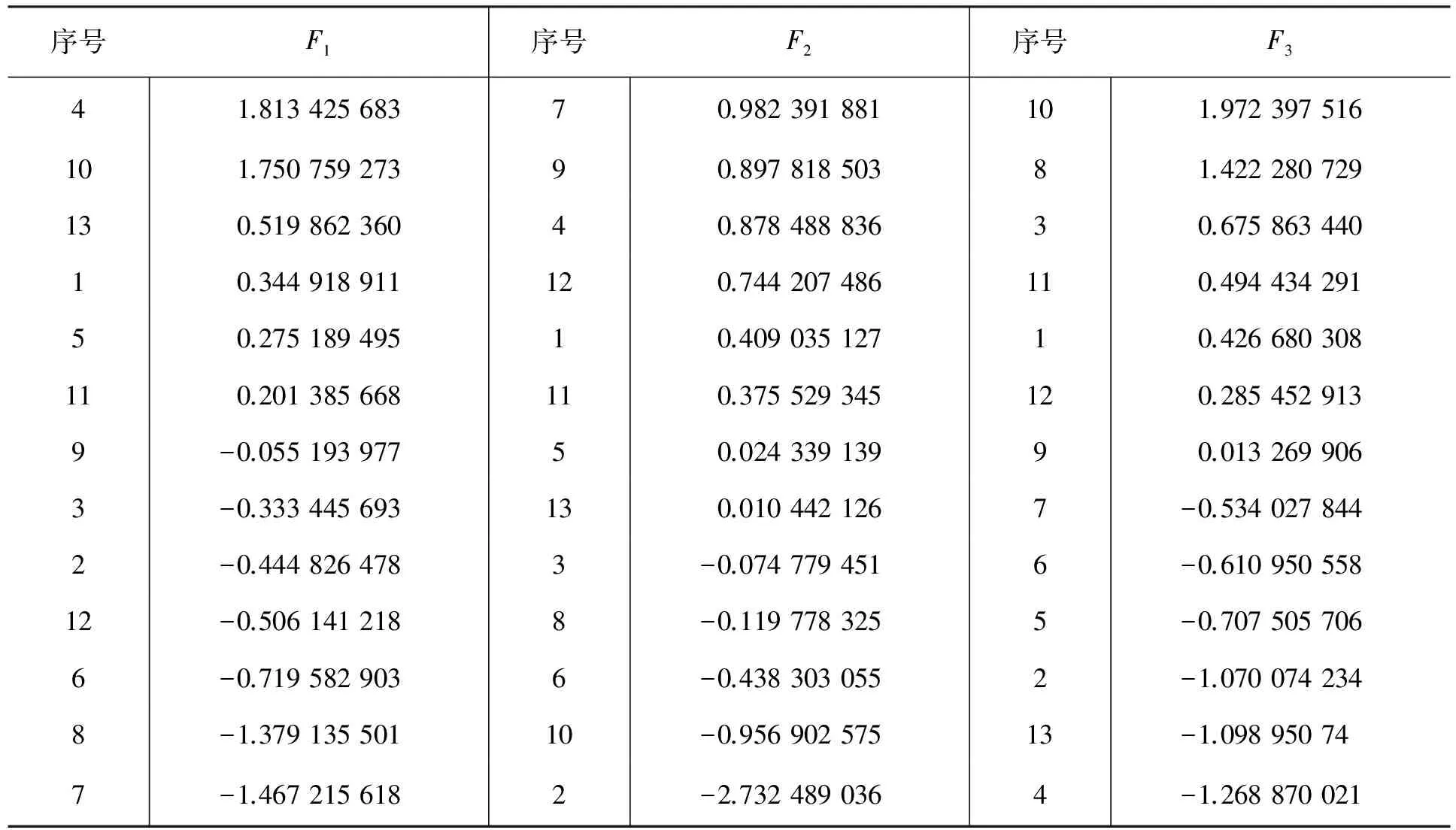
表3 整理后因子得分排序
由整理出的因子得分排序表可以看出,4号教师的F1得分最高,意味着他的学生成绩分布最均匀,其他老师按得分依次排列;7号教师的F2得分最高,这就意味着他所教学生的平均值中位数等指标值最高,意味着他的学生总体平均成绩最好;而对于F3,我们可以看出10号教师的得分值最高,也就意味着他的学生中低分成绩的人数较多。
2.2.3 聚类分析
对标准化后的教师信息数据进行聚类分析[7]。文中选取重心法和最小值法两种方法同时进行分析,并比较分析结果。聚类分析SAS程序如下:
proc cluster data=b1 method=sin pseudo; /*进行聚类分析*/
id tno;
proc tree horizontal;
id tno;
proc cluster data=b1 method=cen pseudo;
id tno;
proc tree horizontal;
id tno;
run;
教师分类两种树状图如图1所示。
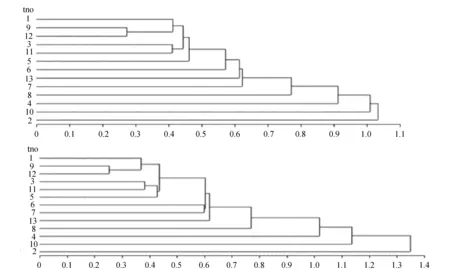
图1 教师分类两种树状图
由图1可大致将数学老师分成3个类别:第一类是第1、3、5、9、11和12号教师,第二类是第6、7和13号教师,最后一类是第2、4、8和10号教师。
2.3 学生成绩分析
2.3.1 对班级和科目进行多因素的方差分析[8]
选取一个学院里考试科目相同的所有学生成绩,按照班级进行分类。由数据可知,我们选取了4个班级共计132人11科的考试成绩。科目分别为:大学生计算机基础、大学外语、高等数学、军事技能训练、军事理论、思想道德修养与法律基础、体育、无机化学、无机实验、心理健康教育和学科概论。我们用x1~x11分别代表这11个学科。对数据进行多因素的方差分析时,选择使用SAS软件中的GLM过程步,在使用GLM过程进行方差分析时,各语句和ANOVA过程基本一致。
datayhuasheng; /*建立数据集*/
inputabgrade@@;
cards;
1 1 66
1 1 80
1 1 87
1 1 75
1 1 89
1 1 76
1 1 75
. . .
. . .
4 11 80
4 11 80
4 11 70
4 11 80
;
%macrocalc(xueyuan,am,bm); /*对数据进行多因素方差分析*/
procglmdata=&xueyuan;
class&am&bm;
modelgrade=&am&bm;
run;
%mendcalc;
%letxueyuan=yhuasheng;
%letam=a;
%letbm=b;
%calc(yhuasheng,a,b)

表4 总体方差分析

表5 方差分析
因为方差分析F=30.51,P<0.000 1,可见拒绝原假设H0,说明模型具有统计意义。对于a,F=4.83,P=0.002 4,可见拒绝原假设H0,说明不同班级对学生成绩具有显著性差异。对于b,F=38.21,P≤0.000 1,可见拒绝原假设H0,说明不同科目对学生也具有显著性的统计意义。可以看出,以班级学生的平均成绩进行方差分析时,班级间的差异性并不明显,只有对班级内每个学生的成绩进行分析时,才能看出班级间的显著性差异,这说明了学生个体间的差异性较大,平均成绩不能完全代表这个班级的综合信息。
2.3.2 对同一专业学生成绩进行因子分析
对班级内学生成绩进行因子分析时,选用的数据是某班级34名同学全部11科(科目同2.3.1)的成绩,共有374个数据。仍然用x1~x11分别代表这11个学科。程序[9]SAS如下:
%macrocalc(yxueyuan,hxueyuan,fm2,fm1407,fs1407,xm1,xm11); /*对数据进行因子分析*/
procstandarddata=sasuser.&yxueyuan;
out=&hxueyuanmean=0std=1;
var&xm1-&xm11;
run;
procfactordata=&hxueyuanrotate=varimaxreorderSCOREOUTSTAT=out&fm2;
var&xm1-&xm11;
run;
procscoredata=&hxueyuanscore=out&fm1407out=out&sm1407;
run;
%mendcalc;
%letyxueyuan=yhuasheng;
%lethxueyuan=hhuasheng;
%letfm2=f2;
%letfm1407=f1407;
%letsm1407=s1407;
%letxm1=x1;
%letxm11=x11;
%calc(yhuasheng,hhuasheng,f2,f1407,s1407,x1,x11)
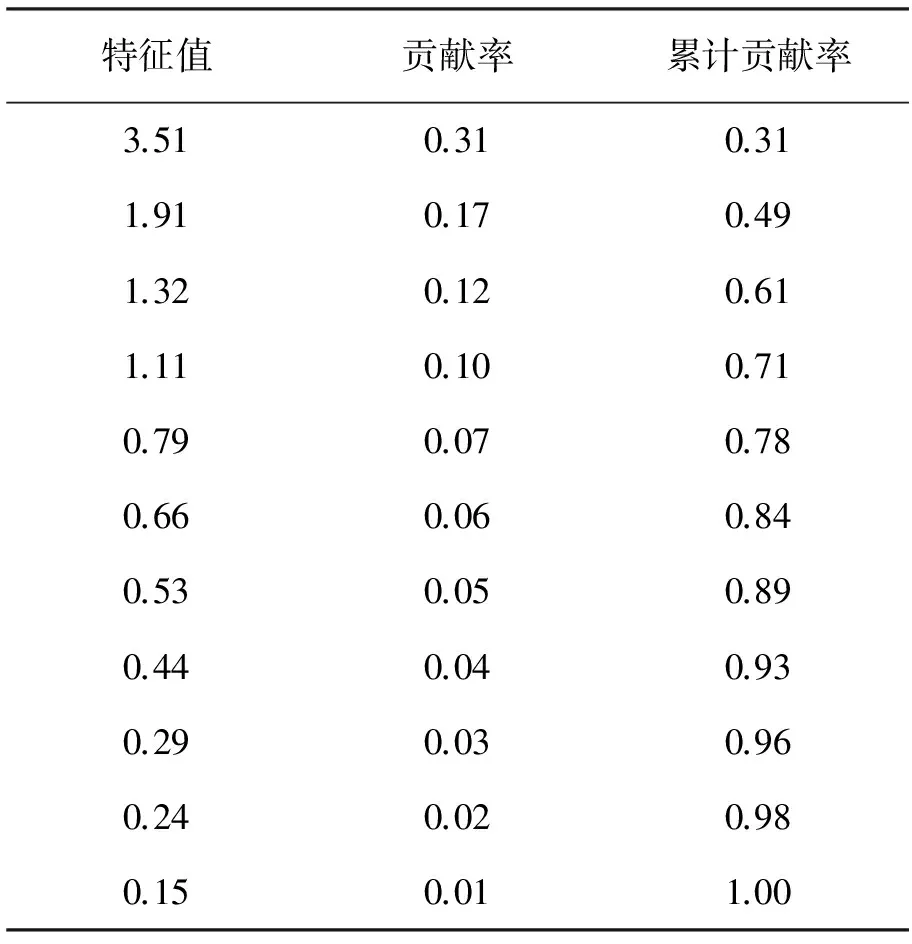
表6 特征值、贡献率、累计贡献率
因此,我们选取前4个因子进行分析。输出的因子载荷见表7, 通过观察分析可以看出,因子F1支配的指标有x1、x2、x3、x5、x8和x11,分别是大学生计算机基础、大学外语、高等数学、军事理论、无机化学和学科概论,它们是理论型课程,所以我们把F1称作是理论型因子;因子F2支配的指标是x4和x9,分别是军事技能训练和无机实验,是需要动手实践的两门课程,因此,把F2称作是动手能力因子;因子F3支配的指标是x7和x10,分别是体育和心理健康教育,他们都是个人综合素质层面上的指标,所以我们认为F3是个人综合因子;因子F4支配的是x11,代表的是思想道德修养和法律基础,它代表的是政治思想因子。
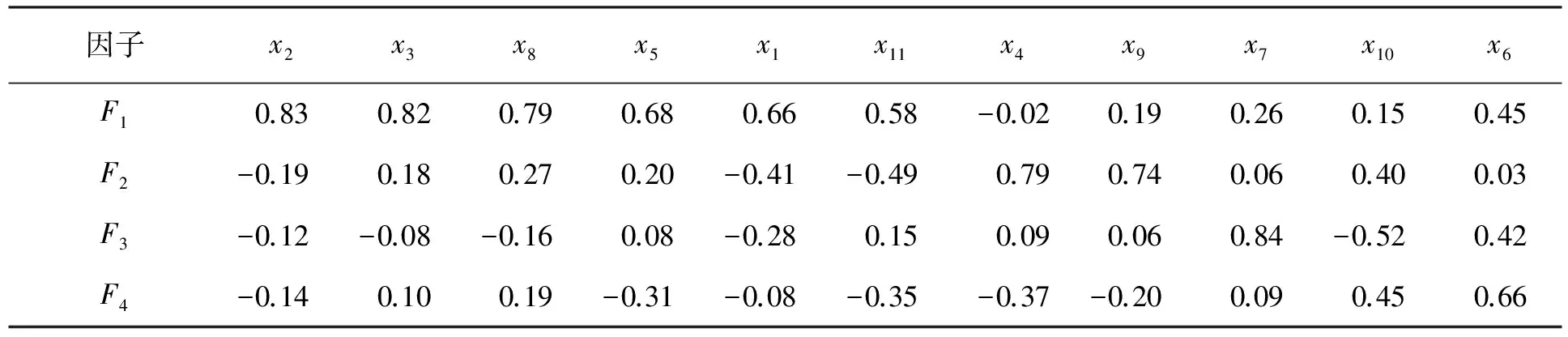
表7 因子载荷表
由整理出的因子得分排序表可以看出,F1得分高低意味着理论型课程成绩的好坏;F2得分的高低意味着动手实践能力的强弱;F3得分的高低代表着个人综合的身心素质的高低;F4得分的高低代表着政治思想的高低。
2.3.3 对学科间相关性进行典型相关分析[10]
从实际角度出发,我们知道不同专业的学生所学基础课程是大体相同的,但所学专业知识不尽相同。有些同学喜欢专业知识,有的同学却对基础性理论知识感兴趣。于是,针对同一专业的学生进行专业学科与基础学科成绩的典型相关分析,来判断两种性质的学科间是否存在某些相关性。
选取某年级4个班的132名学生成绩进行分析,其中专业课为:无机化学x8、无机实验x9和学科概论x11;公共课为:大学生计算机基础x1、大学外语x2、高等数学x3、军事技能训练x4、军事理论x5、思想道德修养与法律基础x6、体育x7和心理健康教育x10。
我们对4个班的总成绩进行典型相关分析。其中变量x8、x9和x11一组,其余变量为一组。SAS程序[11]如下:
%macro calc(dxueyuan,dgonggong,dzhuanye); /*对数据进行典型相关分析*/
proc cancorr all data=sasuser.&dxueyuan
vprefix=&dgonggong vname='公共课'
wprefix=&dzhuanye vname='专业课';
var x1-x7 x10;
with x8 x9 x11;
run;
%mend calc;
%let dxueyuan=dhuasheng;
%let dgonggong=gonggong;
%let dzhuanye=zhuanye;
%calc(dhuasheng,gonggong,zhuanye)
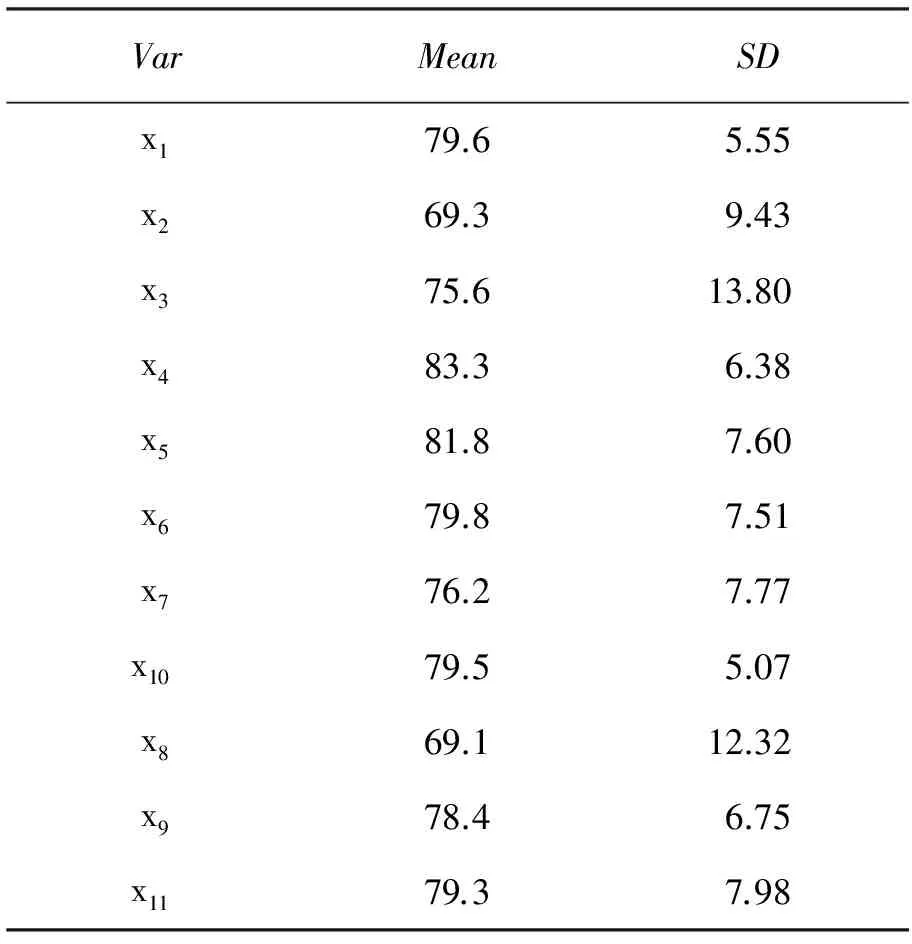
表8 均值和标准偏差
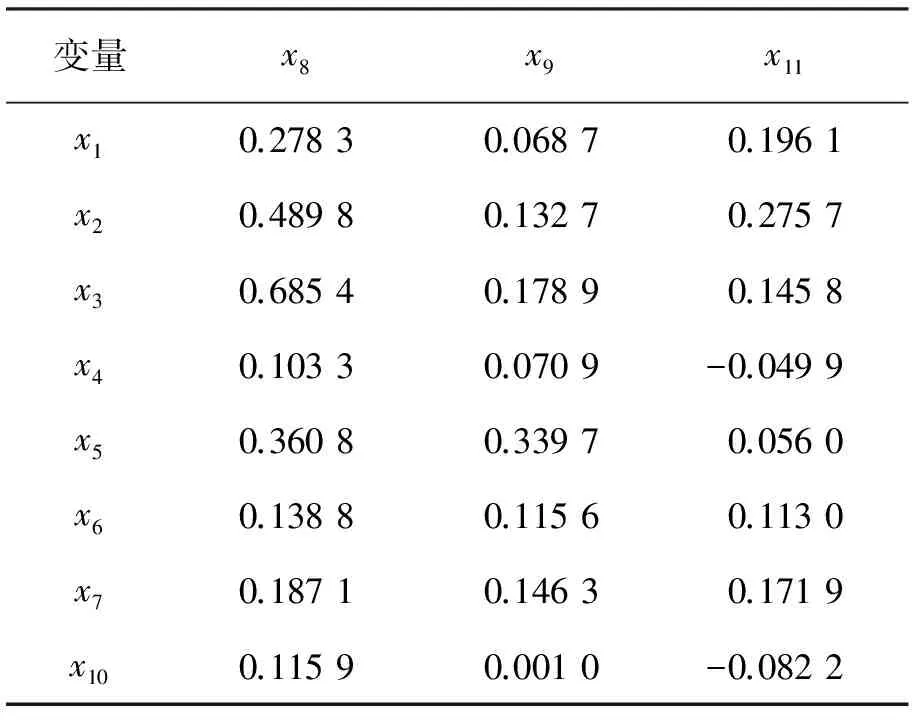
表9 两组变量间的相关系数表

表10 典型变量检验表
由表8和表9给出了两组课程变量的基本信息之间的相关系数,可以粗略看出,这些课程之间有着不同程度的相关性。表10给出了两组课程变量的典型相关系数。 第一对典型相关系数达到0.738 9,可见公共课和专业基础课之间的相关系数很大。表11输出结果显示3对特征值所占方差信息量的比例分别是0.839 3、0.109 0和0.051 7,通过假设检验的p值,我们也可以看出前两对典型变量均是显著的。选取前两对典型变量。

表11 典型相关分析贡献率表
4种检验方法对各典型相关系数为零的假设检验,可以看出4种检验方法均通过。见表12。
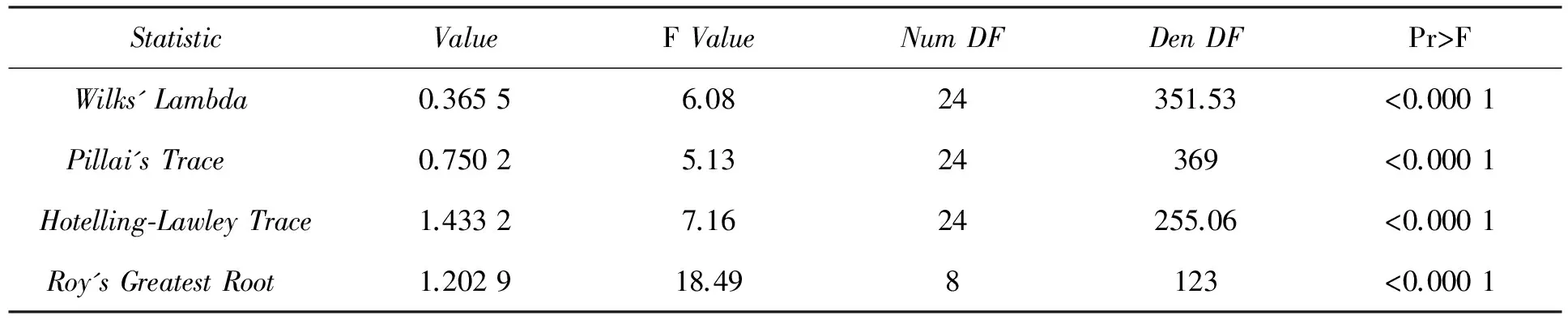
表12 4种检验方法

表13 公共课组典型系数
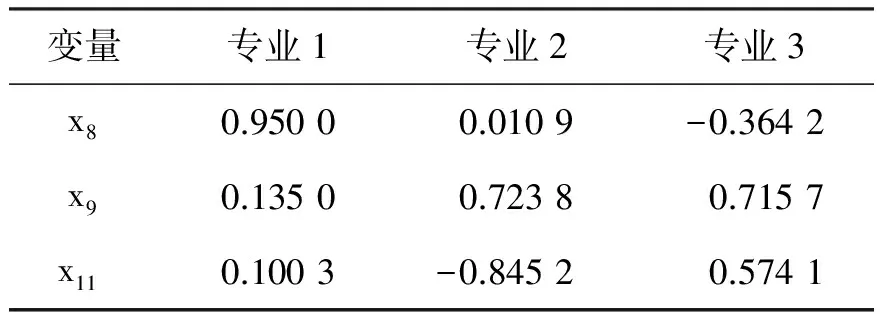
表14 专业课组典型系数表
通过表13和表14可以看出,不论是公共课的8个变量还是专业课的3个变量与第一典型变量的相关系数皆为正。
公共课典型相关表与专业课典型相关表分别见表15和表16。

表15 公共课典型相关表
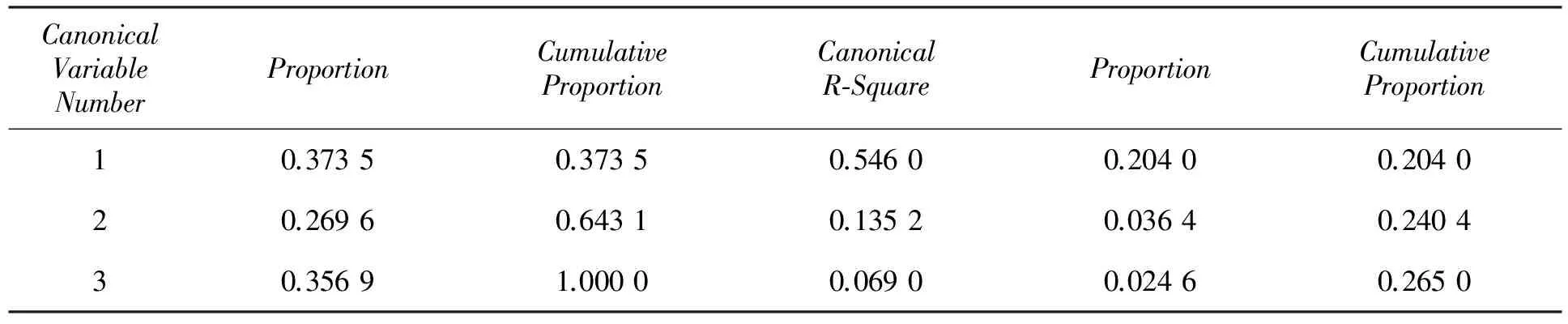
表16 专业课典型相关表
由表15和表16可知,在公共课组变量的组内变异表示第一典型变量能解释变量组0.245 1的组内变异;而表示来自第二个组的第一典型变量可以解释第一个组0.133 8的组内变异。对于专业课组,它们的组内变异表示第一典型变量能解释变量组0.373 5的组内变异;还表示来自第一个组的第一典型变量可以解释第二个组的0.204的组内变异。
可以从相关系数的角度解释典型变量,见表17。
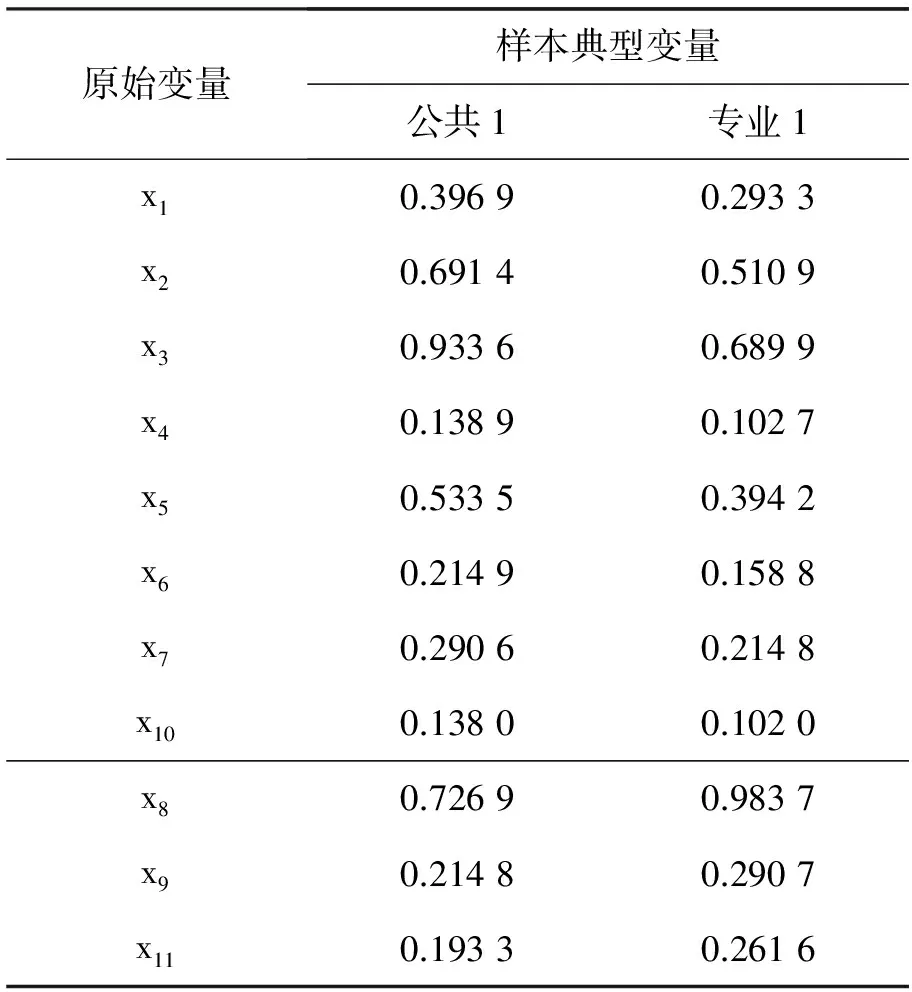
表17 原始变量与典型变量的样本相关系数表
根据表17典型相关系数,公共1主要代表了学生的大学外语和高等数学两个变量,其他的变量显得并不是那么重要,而专业1主要是代表了学生的无机化学这个变量。无机化学变量与第一典型变量公共1有着很大的联系。故公共1可以解释为专业基础变量。这与基于典型系数的解释基本相一致。而专业1主要代表了无机化学变量,专业1主要解释了基础公共课外语和数学对无机化学的影响。这与基于典型系数的解释基本一致。可见专业课和公共基础课之间有一定程序的相关性。
3 结 语
通过实证分析,利用SAS软件对数据进行分析,对教师教学效果评价提供了有利的思路和工具;也减少对学生综合评价的主观因素,以客观的方式来了解学生的综合成绩,为教师有针对性地指导学生,真正实施因材施教提供理论指导。
[1] 朱琳,闫霏霏.基于SAS的高校学生成绩抽样及统计推断:以东华理工大学期末试卷抽样为例[J].东华理工大学学报:社会科学版2015,34(3):280-283.
[2] 王学民.应用多元分析[M].3版.上海:上海财经大学出版社,2009.
[3] 王纯杰,李群,董小刚,等.基于K-均值聚类的多值有序Logistic回归模型在信用卡信用评级中的应用研究[J].吉林师范大学学报:自然科学版,2016,37(3):72-81.
[4] 马燕.主成分分析法在学生成绩评价中的应用[J].乐山师范学院学报,2007,24(1):131-133.
[5] 汪海波,罗莉.SAS统计分析与应用从入门到精通[M].北京:人民邮电出版社,2013.
[6] 黄培丽.多元统计在高校学生成绩统计分析中的应用研究[D].西安:西安建筑科技大学,2013.
[7] 谭庆.基于K-means聚类算法的试卷成绩分析研究[J].河南大学学报:自然科学版,2009,39(4):412-415.
[8] 张琼.利用SAS软件包对学生的考试成绩做统计分析[J].成功(教育),2011(12):204.
[9] 姚鑫锋,王薇.SAS统计分析实用宝典[M].北京:清华大学出版社,2013.
[10]KuiyuanLi,JosaphatUvah,RaidAmin.PredictingStudents’PerformanceinElementsofStatistics[C]//US-ChinaEducationReviewA10,2012:875-884.
[11] 刘洪亮,汪明杰.SAS软件在学生成绩相关性分析中的应用[J].林区教学,2012(4):16-18.
SAS statistical analysis for college student achievements and teaching effect
DONG Xiaogang, TONG Zhizhen, WANG Chunjie*, LI Chunjing, ZHANG Qianqian
(School of Basic Sciences, Changchun University of Technology, Changchun 130012, China)
Taking the student’s final examination results from a college in different major at same semester as references, the multivariate statistical method is used, with SAS macro program, to batch process the examination results and evaluate the teaching effect.
principal component analysis; factor analysis; cluster analysis; canonical correlation analysis; SAS.
2017-02-15
高等学校大学数学教学研究与发展中心项目(2014); 吉林省高等教育教学改革研究课题(2015); 吉林省教育厅十三五科学技术研究项目(吉教科合字[2016]第316号)
董小刚(1961-),男,汉族,吉林长春人,长春工业大学教授,博士,主要从事数理统计方向研究,E-mail:dongxiaogang@ccut.edu.cn. *通讯作者:王纯杰(1978-),女,汉族,辽宁辽阳人,长春工业大学副教授,博士,主要从事统计学和教学方法研究,E-mail:wangchunjie@ccut.edu.cn.
10.15923/j.cnki.cn22-1382/t.2017.3.01
O 213.9
A
1674-1374(2017)03-0209-09

