基于结构方程模型的住宅价格波动影响因素

秦喜文， 李巧玲， 林萍萍， 董小刚， 吕思奇

(1.长春工业大学 研究生学院， 吉林 长春 130012; 2.长春工业大学 基础科学学院， 吉林 长春 130012)



基于结构方程模型的住宅价格波动影响因素

秦喜文1，2， 李巧玲2， 林萍萍2， 董小刚2， 吕思奇2

(1.长春工业大学 研究生学院， 吉林 长春 130012; 2.长春工业大学 基础科学学院， 吉林 长春 130012)

运用供需理论来分析住宅价格波动机理，定性分析住宅价格波动影响因素并构建结构方程模型。通过实证分析和假设检验优化了该结构方程模型。利用二阶因子模型进一步研究和评价近年来国内住宅市场房价波动，得出了影响市场供需的主次因素。

房价波动； 市场供需； 影响机理； 结构方程模型

0 引 言

我国房地产行业的改革始于1998年，《关于进一步深化城镇住房制度改革，加快住房建设的通知》文件颁布之后，房价便开始连续、快速地增长，不仅加重了民众购房支出的负担，甚至导致部分人买不起房，造成了“民生”问题。同时，房地产经济易积累风险，引发经济危机和国家宏观经济的大幅波动。目前，我国房地产市场存在着供需不均衡、住宅市场空闲与过量需求并存等矛盾。

对于住宅市场供需与住宅价格波动的关系研究很多，国外学者David Miles[1]认为影响房价的因素有持续下降的利率、实际上涨的收入及人口上升等；Englund[2]以OECD中的15个国家房地产价格作为研究对象，得出GDP增长与房价是正相关，但利率与房价是负相关的结论；Mintseris[3]认为在90年代中期至2006，存在着房地产泡沫，房地产泡沫出现原因主要是借贷利率。国内学者牟芳华[4]得出住宅市场有效需求的评价指标为人均国内生产总值、居民家庭人均可支配收入、房价收入比、恩格尔系数、居民家庭人均消费性支出、人均居住消费占消费性支出的比重、贷款利率和首付比率；何平[5]指出我国大中城市的房地产仍以开发商品房为主，经济适用房开发总量却很少，而廉租房开发基本空白，造成部分城市商品房房价虚高，空置面积增多。

综上所述，对于住宅价格波动的分析，国内外学者基本上达成一致,即住宅市场供需是影响住宅价格波动的最根本因素。目前，针对住宅市场需求方面的探讨，不论是理论还是实证均取得较多的研究成果。但与市场供给结合方面，大部分还是从理论层次分析，或者是从房地产供给结构、供给数量等方面研究，缺乏实证方面的研究。一方面受数据来源的限制，另一方面由于不同学者针对同一个问题出发点不同或选取的方法及验证模型不同而得出的结论也不一而足。

1 影响住宅价格波动的供需因素分析

影响住宅供给的主要因素有：

1)房屋竣工面积。当年竣工面积上升时，住宅供给量上升，价格也随之上升；反之，年竣工面积下降，房价也就下降。

2)土地成本。影响房产商的总成本，因此直接影响到住房供给的变化。

3)土地有效利用率。指已使用的土地面积与土地的总面积之比,此比率越高越好，即房地产开发企业本年土地开发面积的完成量越多，房地产市场越繁荣。

4) 未来预期。

5)商品房/住房空置率。指某一个时刻空置房面积与房屋总面积的比值，影响供房需求平衡。

6)城镇人员就业率。

影响住宅市场需求因素主要有以下6个方面：

1)城镇居民人均可支配收入。其高低直接决定了居民购买力的大小，最终影响着市场需求量的大小。

2)房价收入比。指住宅价格与城镇居民家庭收入之比，是衡量城镇居民家庭住宅购买能力的重要指标，反映其能否买得起住房。

3)住宅消费支出比。指住宅性消费支出与居民全部消费支出之比，房地产价格的波动会对消费起调节作用。

4)城镇化水平。城镇化水平的提高必然引起大量的农村人口进入城市，使城市规模日益扩大，居民数量不断增加，对城镇住宅提出了更多的要求。

5)首付比例。指购房者第一次支付款项占房款的比例，其变化短期内对房价有影响[6]，根据国家当时的政策而确定。

6)利率。其对房价影响的传导机制是：利率提高(降低)→支付压力增加(减小)→住房供给增加(减少)→房价下跌(上涨)。

2 结构方程模型概述

结构方程模型(Structural Equation Model， SEM)由瑞典统计学家Karl G.Joreskog于20世纪70年代中期提出，是一种基于变量协方差矩阵来分析变量之间的统计方法，结合了因子分析和路径分析，其核心的概念由建立潜在变量的测量模型和结构关系模型两部分组成。

1)建立潜在变量的测量模型是用一些可观测变量来推测和反映潜在变量的变化特征，其构成的数据模型是因子分析[7]。测量模型可分为外生变量的测量模型和内生变量的测量模型,相应的方程可表示为:

(1)

(2)

式中:X,Y----分别为外生和内生指标;

ξ,η----分别为内生和外生潜在变量；

δ,ε----分别为X和Y的测量误差；

ΛX----X指标与外生潜在变量的关系；

ΛY----Y指标与外生潜在变量的关系。

因子分析方法可分为探索性因子分析与验证性因子分析。其中验证性分析是在已经知道影响因素的前提下，验证收集的样本数据与预先确定的结构是否保持一致，目的在于检验预先确定的模型与采集样本数据的拟合程度[8]。由于验证性因子分析能够克服探索性因子分析的局限，所以文中采用验证性因子分析。另外也采用了二阶因子分析，由于在一阶因子分析中发现一阶因子存在中高度的相关性，故沿用一阶因子分析的思路，将这几个一阶因子进一步归结为更高的因子，也可测算出每个一阶因子对高阶因子的影响程度。

2)建立结构关系模型反映的则是各潜在变量之间相互作用的关系,主要使用路径分析。结构模型的方程可表示为：

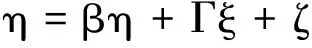
(3)

式中:β----内生潜在变量的关系；

Γ----外生潜在变量对内生潜在变量的影响；

ζ----模式内未能解释的部分。

结构方程主要用于变量间的因果分析,根据一定的理论和假设建立起相应的因果模型,并容许模型中含有自变量、中间变量、潜在变量,同时容许各变量有测量误差,借助于这个因果模型,就可以对复杂的因果结构关系进行合理的分析和解释[9]。

3 实证分析

将住宅价格波动、市场需求与供给作为模型中的潜变量，其中住宅价格波动为外生潜变量，市场需求与供给为内生潜变量。根据上面对住宅市场房价波动影响因素的定性分析，得出住宅市场房价波动的指标体系,见表1。

表1 住宅市场房价波动的指标体系

给出房价波动影响机理概念模型，如图1所示。

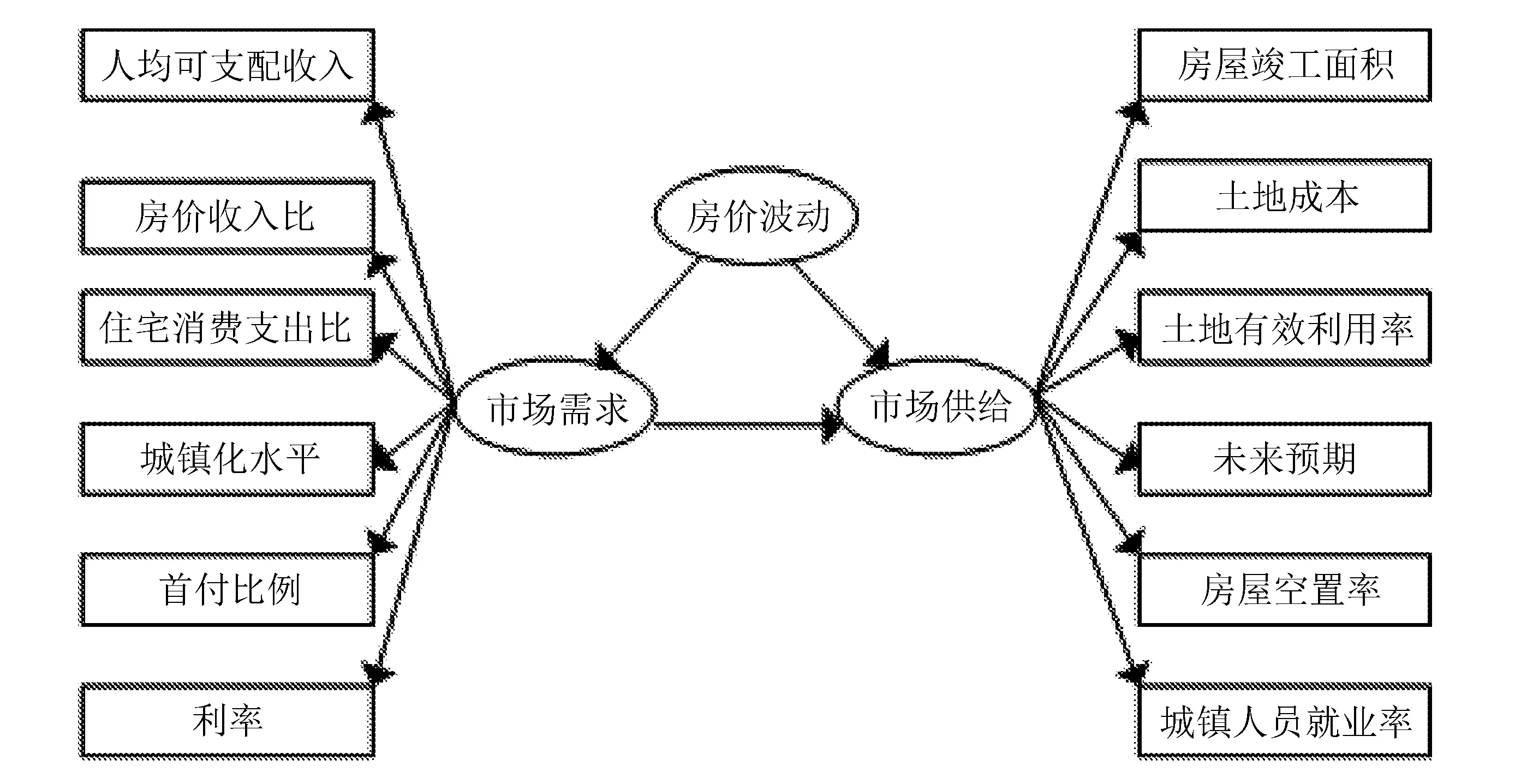
图1 房价波动影响机理概念模型

所用数据来源于《中国统计年鉴》、《中国房地产统计年鉴》以及国家统计局官网。

为检验各测量指标合理性及对住宅市场价格的影响程度，将构建一阶验证性因子分析模型M1，重在探究影响住宅市场供需不均衡的主要因素并寻求在该样本下达到的最优模型，常用的检验指数有GFI、AGFI、PGFI、CFI、RMSEA等，文中涉及到的检验指标见表2。

表2 模型拟合指数

3.1 一阶验证性因子分析

根据研究分析得出的结构方程模型进行验证性因子分析，模型中涉及到两个潜变量。检验结果见表3。

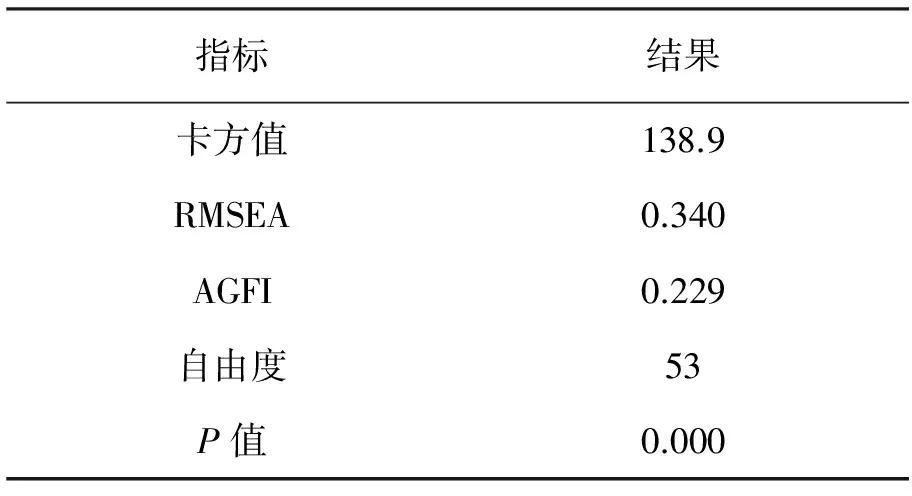
表3 模型M1拟合检验结果

可识别并得到模型的卡方检验统计量为138.9，自由度为53，其中RMSEA=0.340>0.08，AGFI=0.229<0.90,显示出假设模型的适配度不理想，故而对模型进行修正，修正指数见表4。

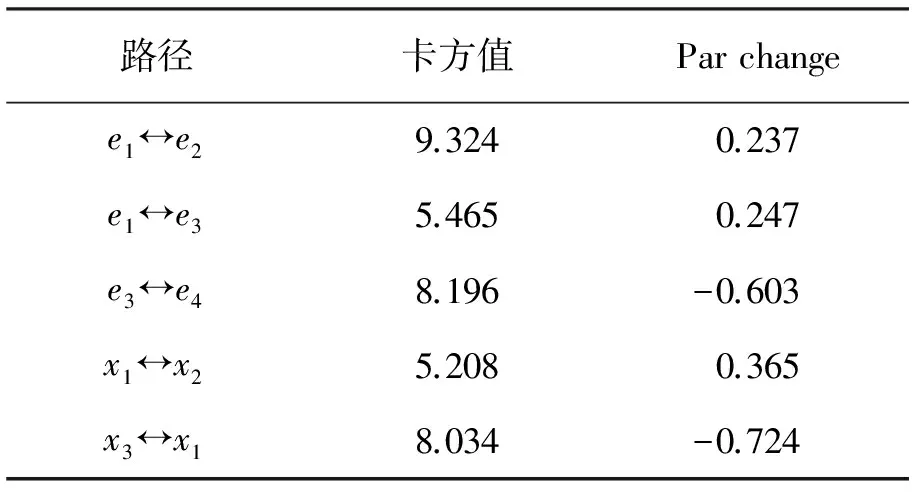
表4 模型M1修正指数

由表4及表2知，x1与x2之间的相互影响力为0.365，误差的相互影响力为0.237，且能缩小的卡方值分别为5.208 和9.324，构建误差项所能减少的卡方值居第一位。x3和x4之间的相互影响力为-0.724，误差的相互影响力为-0.603，且能缩小的卡方值分别为8.034 和8.196，居于第二位和第三位。e1和e3之间的相互影响力为0.247，能减少的卡方值为5.465，又因为城镇居民人均可支配收入和住宅消费支出比呈现正向影响关系。综上所述，需要在这三对两变量误差项间新建一条路径，即e1和e2、e1和e3、e3和e4。由于模型M1的修正指数表中没有关于x5、x6和y6的修正建议，再结合现实情况，可将它们删除。所以，模型由原来的M1修改成了M2，模型M2路径如图2所示。

模型的检验结果见表5。

表5 模型M2拟合检验结果

由表5可知，各项指标有了显著性的提高，模型拟合检验的卡方值为71.3，自由度为26，模型RMSEA=0.08，勉强达到要求；AGFI=0.78，依然小于0.9，但是相比M1模型有较大的改善,说明M2模型还是有一些逊色。究其原因，一方面是受样本数据的影响，另一方面文中潜变量个数少，但模型M2在该样本下已达到最优状态，说明模型M2与实际情况较接近，具有实际参考价值。

3.2 二阶验证性因子分析

在一阶验证性因子分析的前提下，以住宅市场房价波动为二阶因子，结合模型M2来构建二阶因子分析模型M3。在符合实际的前提下，为保证模型M3的顺利进行，先将住宅市场房价波动和市场需求的系数固定为1，初步的模型M3拟合结果得知，房价收入比(x1)、城镇化水平(x4)、房屋竣工面积(y1)和开发商未来预期(y4)的因子负荷都超过0.95，可认为模型存在很强共线性。模型拟合的卡方值为54.6，自由度为26，p值小于0.05，达到显著性水平，但是RMSEA=0.162>0.08，AGFI=0.53<0.90， 显示假设模型的适配度不理想，因此需要进行模型修正，修正指数见表6。

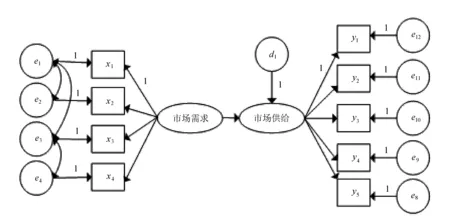
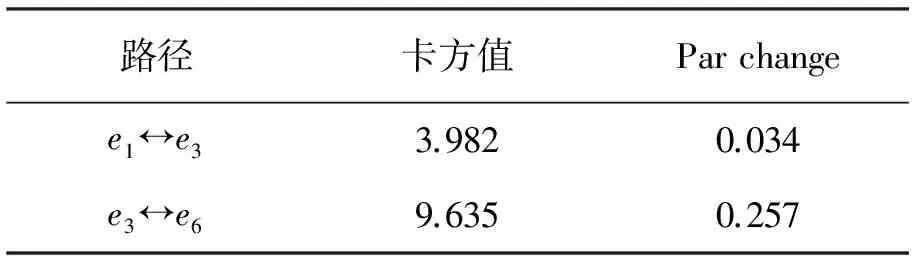
图2 结构方程模型M2

由表6可知，在e3和e6之间构建路径将减少卡方值9.635，减少的卡方值排在第一位。所以先在e3和e6之间增加一条路径，构成模型M4，拟合结果及拟合结果检验如图3和表7所示。

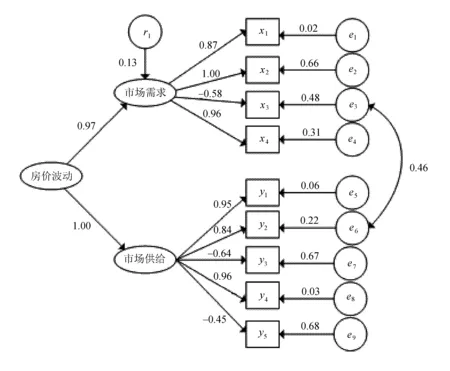
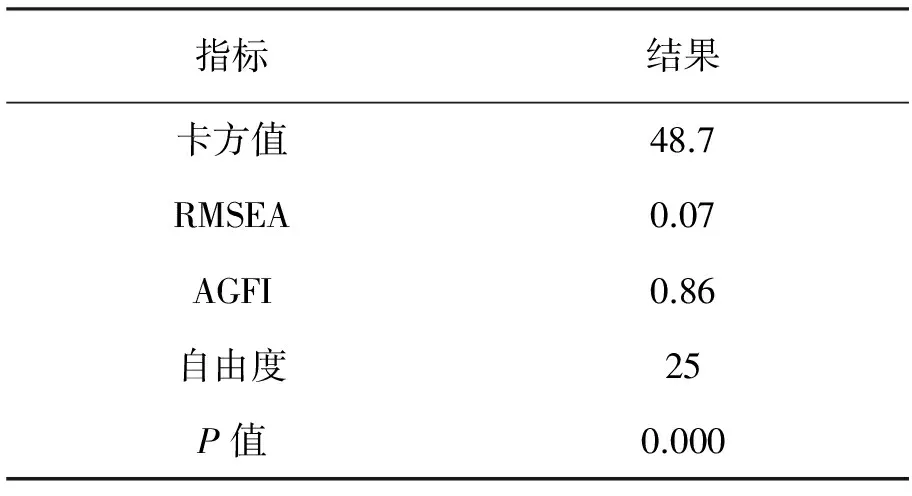
图3 二阶因子分析模型M4拟合结果

在e3和e6之间新增一条路径之后，模型M4的拟合检验结果较为乐观。检验结果的卡方值为48.7，自由度为25，卡方自由度比为1.948，在1～2(严格要求下)范围内，RMSEA=0.07<0.08,说明模型整体拟合程度较好，AGFI=0.86，虽然未达到0.9，不够理想，但也差别不太大。模型不够优秀的原因同一阶模型M2一样，都是由于样本数据本身的影响及潜变量个数受限，但模型M4在该样本下达到最优，同时达到了其他适配度检验标准，说明模型M4较接近于实际情况，也具有实际的参考价值。

4 结论与讨论

通过上述分析研究以及多次模型修正，最终得到比较理想的一阶分析模型M2和二阶分析模型M4。由模型M2可知，市场需求与市场供给的路径系数达到0.64。模型M4阐明住宅市场房价波动、市场供需与各测量指标之间的相关度。通过对比模型M2和模型M4的拟合结果，发现住宅市场供需与各测量变量的关系几乎保持一致，也就是说影响房价波动的是市场供需。

在需求分析中，城镇化水平与城镇居民人均可支配收入的提高会导致住宅消费支出比变高，此外,由于城镇化水平又可以使城镇居民人均可支配收入提高，所以此三项中保留城镇化水平一个因素即可。银行贷款利率和首付比例在结构方程模型中与住宅市场需求的相关度并不强烈，也符合现实，故而将其剔除。由路径图得知保留的两个因素对市场需求的影响程度强弱依次为：房价收入比→城镇化水平。在供给分析中，根据实际数据分析结果剔除了y6并由径图得出，剩余5个因素对市场供给影响程度强弱依次为：未来预期→房屋竣工面积→土地成本→土地有效利用率→商品房空置率。

利用我国住宅市场的实际数据，构建了一套完整系统的评价影响住宅市场房价波动的体系，并指出影响供给与需求各方因素的强弱系数，可为政府对房价的管控提供有效参考。另外，文中只是从微观方面来分析住宅市场影响因素的，并没有考虑宏观因素如经济、社会和行政等对住宅市场的影响，在进一步的研究中可以将这些作为重点加以考虑。

[1] Miles D, Pillonca V. Financial innovation and european housing and mortgage markets[J]. Oxford Review of Economic Policy,2008,24(1)：145-175.

[2] Englund P, Ioannides Y M. House price dynamics: An international empirical perspective[J]. Journal of Housing Economics,1997,6(2)：119-136.

[3] Mintseris J, Pierce B, Wiehe K, et al. Integrating statistical pair potentials into protein complex prediction[J]. Proteins,2007,69(3)：511-520.

[4] 牟芳华.城镇居民住宅消费统计指标体系的构建[J].江苏统计(指导价格),2001(3)：19-20.

[5] 葛杨,何平.中国城镇住房供给结构对住房价格的影响[D].南京：南京大学，2012：15-17.

[6] 韩立达,肖云.购房贷款首付比例变化对房地产市场的影响分析[J].财经漫笔,2008(1):90-91.

[7] 周旭武.结构方程模型方法的实现与应用[D].大连:大连理工大学,2009.

[8] 刘金兰,何涛.结构方程模型的偏最小二乘算法及其几何意义[J].哈尔滨商业大学学报:自然科学版,2005(6):776-780.

[9] 刘敦南,刘睿智.基于结构方程的电力市场效率优化路径方法[J].电力系统自动化,2016(7):36-41.

Influential factors of housing price fluctuations based on the structural equation model

QIN Xiwen1,2, LI Qiaoling2, LIN Pingping2, DONG Xiaogang2, LYU Siqi2

(1.Graduate School, Changchun University of Technology, Changchun 130012, China; 2.School of Basic Sciences, Changchun University of Technology, Changchun 130012, China)

With supply and demand theory, mechanism of housing price fluctuation is qualitatively analyzed to determine what factors influence the fluctuation, and a structural equation model is built. The model is further optimized with both empirical analysis and hypothesis testing. A second-order factor model is also used to evaluate the price fluctuations in China housing market, for obtaining primary and secondary influential factors in supply and demand market.

fluctuation of housing price; supply and demand in market; influence mechanism; structural equation model.

2016-01-25

国家自然科学基金资助项目(11301036，11226335); 吉林省教育厅科研项目(2014第127号,2013第142号)

秦喜文(1979-)，男，汉族，吉林梅河口人，长春工业大学教授，博士，主要从事HHT理论与应用研究,E-mail:qinxiwen@ccut.edu.cn.

10.15923/j.cnki.cn22-1382/t.2017.3.02

O 157.5

A

1674-1374(2017)03-0218-06