基于凸轮权重距离局部保持投影算法的人脸识别

甘航萍，王 力，何 庆，徐同伟

(贵州大学 大数据与信息工程学院，贵州 贵阳 550025)



基于凸轮权重距离局部保持投影算法的人脸识别

甘航萍，王 力，何 庆，徐同伟

(贵州大学 大数据与信息工程学院，贵州 贵阳 550025)

结合凸轮(Cam)权重距离和局部保持投影算法，提出了一种改进的凸轮权重距离局部保持投影法。该算法主要将局部保持投影算法在选取近邻点并构造加权图时采用的欧式距离用凸轮权重距离代替，克服了处理高维数据中数据分布不均匀的问题。运用该改进的算法对人脸图像进行特征提取，与局部保持投影算法和正交局部保持投影算法进行实验比较，结果证明，用改进的凸轮权重局部保持投影法进行人脸识别得到的识别率更高，算法的性能效果更好。

凸轮权重距离；人脸识别；局部保持投影算法；特征提取

人脸识别技术因其在人机交互系统、公安刑侦、识别验证系统等领域有着良好的应用前景而受到广泛关注。人脸识别技术是从计算机分析的人脸图像或者视频中提取出大量的识别信息，以此来辨别人身份的，是一种最直接、易被接受的生物特征识别技术[1]。

在人脸识别技术中，用于实验的人脸图像的矢量空间的维数过高而增大识别难度，因此特征提取就成为了人脸识别中的重要课题。目前，应用于人脸识别特征提取的方法有多种，常见的特征提取方法有：主成分分析(Principal Component Analysis，PCA)、线性判别式分析(Linear Discriminant Analysis，LDA)、独立成分分析(Independent Component Analysis，ICA)等[2]，但人脸图像大都位于非线性子流形面上，所以一些非线性特征提取法，特别是众多流形学习方法引起了越来越多的注意。经过十多年的不断研究，学者们提出了众多流形学习理论和算法[3]。经典常见的流形学习方法有：局部线性嵌入(Locally Linear Embedding，LLE)、局部切线空间排列(Local Tangent Space Alignment，LTSA)、等距映射(Isometric Mapping，ISOMAP)、拉普拉斯特征映射(Laplacian Eigenmaps，LE)等，这些方法的主要思想是通过局部线性近似将原始高维空间数据的内在几何结构保存下来，描述了人脸图像的非线性分布，揭示了数据的本质特性[4]。文献[5]提出了局部保持投影(Locality Preserving Projections,LPP)算法，将其运用到人脸识别中。文献[6]提出了(Orthogonal Locality Preserving Projections，OLPP)算法，该方法是在LPP算法上进行的改进[7]。LPP算法在前期选取近邻点并构造加权图时采用的是欧式距离，其前提是数据为均匀正态分布的。而实际应用中，绝大多数高维空间数据并非均匀正态分布。后来Zhou等人提出了一种Cam权重距离，其最先用于最近邻分类器[8]，后来Pan等人将该权重距离应用于LLE算法中并获得了良好的降维效果[9]。

基于以上启示，为了更加合理的解决数据分布不均匀的问题，并有效的提高识别率，本文结合Cam权重距离和LPP算法，提出了Cam权重局部保持投(Cam Weighted Locality Preserving Projection，Cam-WLPP)算法，将该算法在Matlab平台上进行人脸识别仿真实验，并与LPP算法和OLPP算法进行对比，实验结果验证了该改进算法的有效性和优越性。

1 局部保持映射算法

局部保持映射算法(LPP)主要思想是通过给定输出的线性映射关系取代拉普拉斯特征映射算法(LE)中的非线性映射关系，从而实现从高维观测空间到低维特征空间的线性映射[10]。事实上，LPP算法目的在于找到一组最优投影矢量数据集使得样本空间的局部离散度最小，即让原始空间内互相靠近的样本在变换的低维空间内依旧互相靠近[7]。

LPP算法的基本思想[11]：设 表示为一副人脸图像的一维向量，LPP算法的主要目的就是保留数据的内在几何特征和局部结构，其优化函数是

min∑i,j(yi-yj)2wij

(1)

其中，yi为xi的低维映射，即yi=WTxi，上式中的Sij为xi和xj两个样本的关系矩阵，其定义为

(2)式中，ε为一个非常小的正数，其定义了xi的一个领域半径。式(2)整体表示若xi和xj两个样本点之间的距离很近，已经小于ε的话，则该两个样本的关系为e-‖xi-xj‖2/τ，否则置零。由此，所有的 可以成为样本之间的距离相似矩阵，其用权值来表示样本间的相似程度。

LPP算法引入映射变换yi=WTxi后，式(1)可以转换为

XLXTW=λXDXTWT

(3)

其中，X为N维的训练数据集{x1,x2,…,xN}，映射之后的n维数据集{y1,y2,…,yn}，n≪N；L=D-S是一个拉普拉斯矩阵；D是一对角矩阵，其对角元素对应关系矩阵S相应行或列的元素之和。由于训练样本图像的个数一般远少于一幅图像样本的像素个数，所以XDXT通常是奇异的，为克服这个问题，首先需要利用PCA对图像进行初步的降维，再在降维获后的子空间运用LPP算法，因此，所得的变换矩阵为

W=WPCAWLPP

(4)

2 基于凸轮权重局部保持映射算法

2006年提出的凸轮(Cam)权重距离是一种相似性度量方式，较之欧式距离，Cam权重距离能更合理的解决数据分布不均匀的问题[12-13]。

2.1 凸轮权重距离

定义1 设Y=(Y1,Y2,…,Yl)是服从l维标准正态分布N(0,1)的l维随机向量，则其概率密度函数有

(5)

随机向量X的定义有

(6)

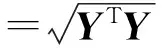
定义2 若随机向量X服从Cam分布X～Caml(a,b,τ)，则对于x～Rl，X的概率密度函数有

(7)

定义3 设x0∈Rl是Cam分布Caml(a,b,τ)的中心，则从x∈Rl到中心点x0的Cam的权重距离为

(8)

若随机向量X～Caml(a,b,τ)，则有

(9)

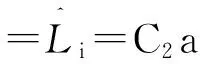
(10)

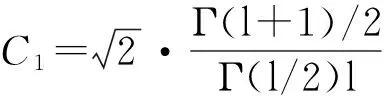
2.2 局部保持映射算法

LPP算法在选取近邻点并构造加权图时，由于绝大多数高维空间数据并非均匀正态分布的，如果依然采用欧式距离判断数据点之间是邻近点，并将相对应的节点连接的话显然不合适，针对此，本文采用Cam权重距离来改进LPP算法原有的构造加权图的方法，有效解决了数据并非均匀正态分布的问题。

Cam-WLPP算法的步骤：

(1)PCA投影。利用PCA算法得到初始降维的投影矩阵，记作WPCA；

(2) 选取近邻点、构造加权图。G为有n个节点的图。第i个节点与人脸图像中的xi相对应，判断数据点xi和数据点xj是否接近；

1)计算xi到所有点的欧氏距离，按从小到大排列距离，得到xi的pw个邻近点，Xi={xi1,xi2,…,xip}，Xi⊂D；

2)获得Vi，其元素值为Vij=xij-xj，其中j=1,2,…,p；

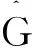
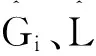
4)根据公式

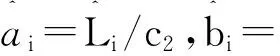
5)根据式(8)，计算xi到任意xi∈D的Cam权重距离；

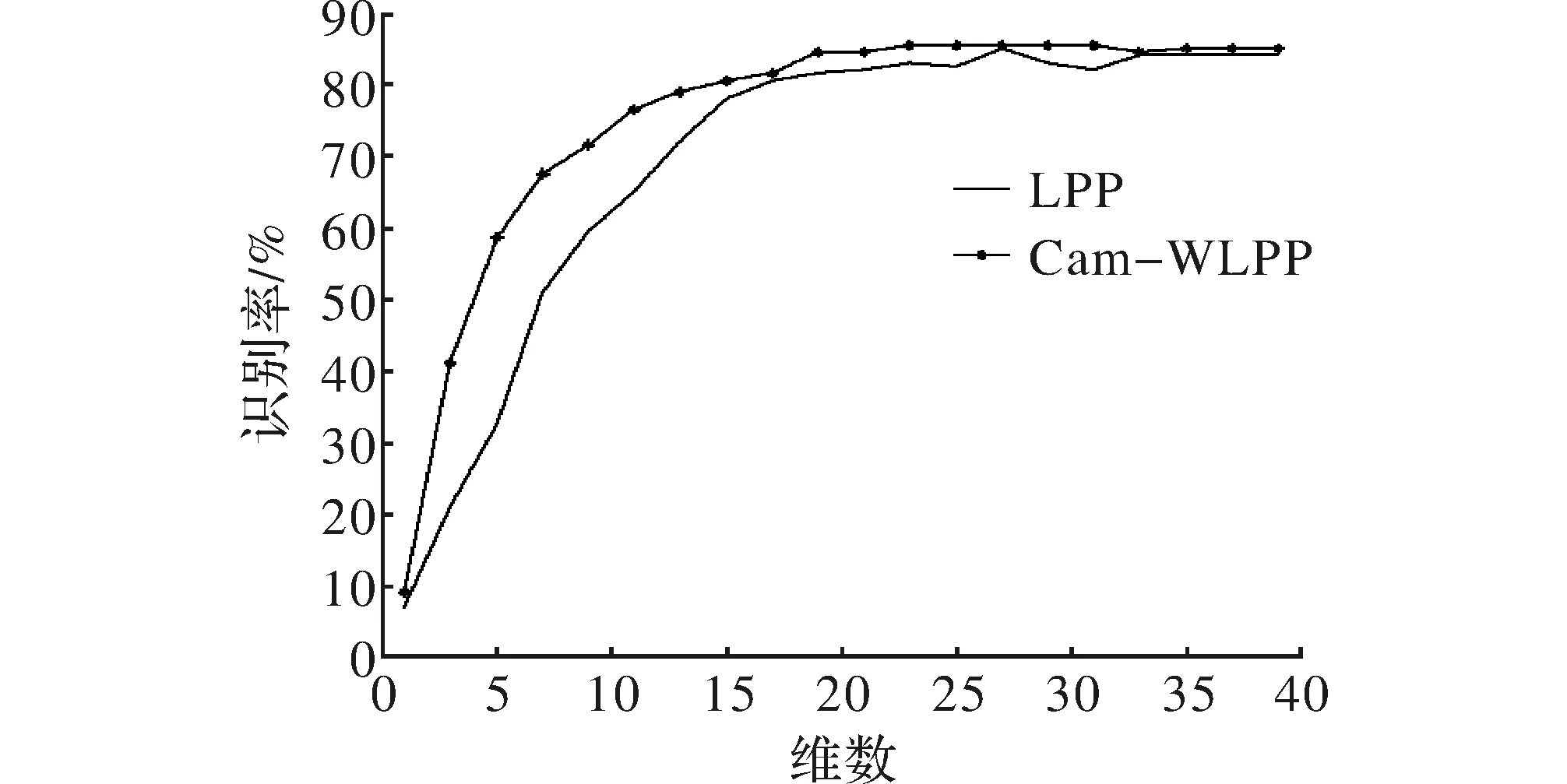
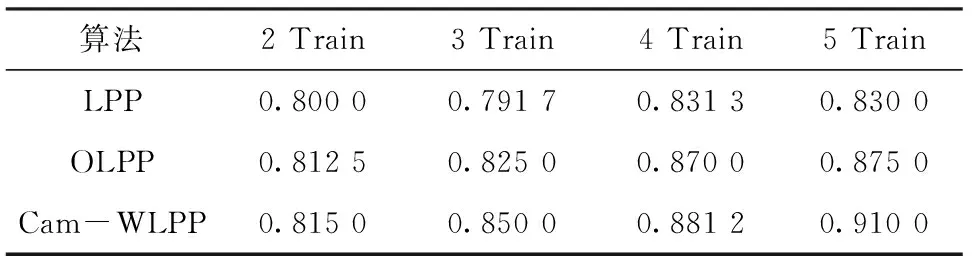
6)若满足Camdist(xi,xj)

(3) 选择权值。若数据点xi和数据点xj是接近的，则给此边赋予权值Sij=e-‖xi-xj‖2/τ，否则Sij=0；

(4)LPP投影。若WLPP=[a1,a2,…,an]，由

XLXTW=λXDXTWT

(11)

求解广义特征向量问题中的特征向量和特征值和特征向量。若将所求的特征值按升序排列λi≤λi+1，选择前d个最小特征值对应的特征向量w1,w2,…,wd，则该d个特征向量就构成了LPP算法的最优投影矩阵WLPP，故最终得到投影矩阵W=WPCAWLPP。

3 仿真实验结果及分析

3.1 仿真实验方案

在Matalab平台上进行人脸识别仿真实验，采用ORL人脸数据库。ORL人脸数据库包含40个人，每个人10幅不同图像，在人脸表情、光照、姿态等细节上有一定变化的400幅人脸图像。本文采用了两种实验对比方案。

方案1 在Cam-WLPP算法中，根据反复试验，将用于估计Cam权重距离的参数pw设置为30，邻域值设置为35；在LPP算法中同样将邻域值设置为35，对比用两种算法得到的识别率随着维数的变化情况。

方案2 每个人的10幅图中选择c幅图(c=2,3,4,5)来作为训练样本，剩余(10-c)幅图作为测试样本。LPP、OLPP、Cam-WLPP3种算法维数选择在30维，仿真实验分别对比用3种算法得到的识别率。

3.2 仿真结果分析

仿真实验结果比较的主要性能指标是识别率。本文仿真实验均是对ORL人脸数据库进行人脸识别所获得的识别率。方案1实验获得的结果如图1所示。

图1 Cam-WLPP和LPP在不同维数下的识别率

如图1所示，Cam-WLPP算法的识别率比LPP算法识别率在整体上有所提高，都在19维之后识别率趋于稳定，在40维之后识别率有些许下降的趋势，这也能估计出，ORL人脸库的本征维数在20～40之间，当最终降维数在这个区间段时，得到的识别率较好，因此在方案2的试验中3种算法选择的维数为30维。方案2实验获得的结果如表1所示。

表1 3种算法在不同训练个数下的识别率

从表1中的结果可以看出，LPP、OLPP、Cam-WLPP3种算法在不同的训练样本数下得到人脸识别识别率结果，OLPP算法优于LPP算法，Cam-WLPP算法优于LPP算法和OLPP算法。

4 结束语

本文提出了一种基于凸轮权重的局部保持投影算法，该算法在人脸识别仿真实验中在性能和解决数据分布不均匀的问题方面优于已有的局部保持投影算法。但是本文改进的算法在实验中得到的识别率还不是很高，下一步的工作重点是进一步对算法进行优化，并能多采用几个常见的人脸数据库进行实验比较，逐步扩大算法的适用范围、提高算法的实际应用能力。

[1] 金一. 基于核的正交局部保持投影的人脸识别中的[J].电子与信息学报,2009,31(2):283-287.

[2] 李政仪,朱益丹,赵龙.基于有监督直接局部保持局部投影的人脸识别[J].计算机工程,2009,35(10):190-192.

[3] 雷迎科.流形学习算法及其应用研究[D].合肥:中国科学技术大学,2011.

[4] 李毅英.邻域结构保持投影及应用[D].西安：西安电子科技大学,2011.

[5] He Xiaofei,Yan Shuicheng,Hu Yuxiao, et al. Face recognition using laplacian faces[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3):328-340.

[6] Cai Deng,He Xiaofei,Han Jiawei,et al. Orthogonal laplacianfaces for face recognition[J].IEEE Transactions on Image Processing,2006,15(11):3608-3614.

[7] 黄璞.基于流形学习的特征提取与人脸识别研究[D].南京:南京理工大学,2014.

[8] Zhou Changyin,Chen Yanqiu.Improving nearest neighbor classification with Cam weighted distance[J].Pattern Recognition, 2006,39(4):635-645.

[9] 黄芮婕.基于流形学习的人脸识别算法研究[D].成都:电子科技大学,2013.

[10] 尹峻松.流形学习理论与方法研究及在人脸识别中的应用[D].长沙:国防科学技术大学,2007.

[11] 赵芬庆.基于LPP的人脸图像分析[D].西安:西安电子科技大学,2013.

[12] 刘元.度量学习及其研究应用[D].无锡:江南大学,2015.

[13] 陈新忠,胡汇涓,王雪松.基于加权近邻保持嵌入的高光谱数据降维方法[J].中国矿业大学学报,2013,42(6):1066-1072.

Face Recognition Based on Locality Preserving Projections Algorithm of the Cam-weighted Distance

GAN Hangping，WANG Li，HE Qing，XU Tongwei

(School of Big Data and Information Engineering,Guizhou University,Guiyang 550025,China)

By combining the weighted distance of the cam and the locality preserving projections algorithm, this paper proposes an improved Cam weighted locality preserving projection method.In this algorithm, the Euclidean distance used to the locality preserving projection algorithm is instead of the Cam weight distance, which overcomes the problem of processing the data distribution in high dimensional data.Compared with the local preserving projection algorithm and the orthogonal locality preserving projections algorithm, the results show that the improved Cam weighted locality preserving projection method is better in face recognition and recognition rate.

cam weighted distance;face recognition; LPP algorithm; feature extraction

2016- 10- 05

贵州省科技厅基金(黔科合LH字[2014]7628)

甘航萍(1990-)，女，硕士研究生。研究方向：图像处理等。王力(1971-)，男，教授。研究方向：模式识别等。何庆(1982-)，男，博士，副教授。研究方向：认知无线网络，无线传感网络等。

10.16180/j.cnki.issn1007-7820.2017.08.002

TN911.73;TP391.41

A

1007-7820(2017)08-006-04