基于CHAN与粒子群算法的协同定位研究

江 凤，吴 飞，王昌志

(上海工程技术大学 电子电气学院，上海 201600)



基于CHAN与粒子群算法的协同定位研究

江 凤，吴 飞，王昌志

(上海工程技术大学 电子电气学院，上海 201600)

针对利用CHAN算法进行TOA定位时，其定位的精度受环境条件的影响程度较大的问题，提出了一种利用粒子群与CHAN算法协同定位的方法。通过粒子群估算出移动终端的初始解，利用初始解构建残差方程，筛选出LOS 环境下对应的基站，并用该基站结合CHAN定位模型对移动终端进行二次定位最终得到位置估计。由实验结果可知，基于融合算法的定位精度比单一算法的定位结果，其定位误差至少降低5 m。

协同定位；CHAN算法；残差分析法；粒子群算法

随着无线通信网络与移动互联网的发展，提供基于地理位置信息的服务(Location Based Service，LBS)已成为具有发展潜力的方向之一。室内定位系统无法通过GPS系统实现，源自室内的建筑结构复杂，障碍物会阻挡信号的正常传输。基于无线局域网(WLAN)的定位技术由于部署成本低，因此拥有广泛的应用市场，成为室内定位主要采用的方法。鉴于终端设备与基站通信时长(TOA)与地理环境密切相关，使用未经过滤的TOA数据进行定位将会导致较大误差[1]。

为有效抑制非视距的环境对信号通信时长所产生的影响，特别是在环境复杂的地理区域中，传统的无线电波传播模型和NLOS分布模型均很难适用，为保证定位的精度，需要对采集的信号通信时长进行分类以筛选出视距环境下的基站，以减少非视距的基站对定位结果造成的误差[2]。

1 模型建立

非视距误差是影响基于无线通信基站定位精度主要而又难以消除的因素之一，也是基于无线通信基站定位系统提高定位精度必须要解决的关键问题之一[3-4]。基于TOA定位的CHAN算法在LOS环境和短距离情况下，测量距离的精度较高，误差较小，但是该算法却必须是在LOS环境下使用才能有较好的定位精度，在NLOS定位时，信号在传输过程中受到障碍物的遮挡，反射或吸收，出现多路径传播的现象，将会导致无法准确定位终端位置坐标[5]。LOS和NLOS的传播示意图如图1所示。

图1 LOS径与非LOS径示意图

本文针对较大NLOS误差会导致位置坐标计算受到影响而引入残差分析法[6]，而针对NLOS误差无法避免的特性引入基站筛选的方式，以滤除非视距造成的定位误差。CHAN算法由于只考虑了系统的高斯噪声误差，没有考虑NLOS误差，因此当实际的环境中出现障碍物遮挡等因素时，仅采用CHAN算法估计终端位置坐标将会造成较大误差。

2 视距与非视距定位描述

本文的TOA数据来源于测量多个基站到同一个移动终端的信号到达时间，根据到达时间计算移动终端到基站的距离，再根据多个距离值估计移动终端的位置[8]。在视距传播的情况下若信号在移动终端和第i个基站之间的传播时间为ti，无线电信号传播速度为c(c=3×108m/s)，设移动终端与基站之间的距离为ri，则ri=c×ti，其传播示意图如图2所示。

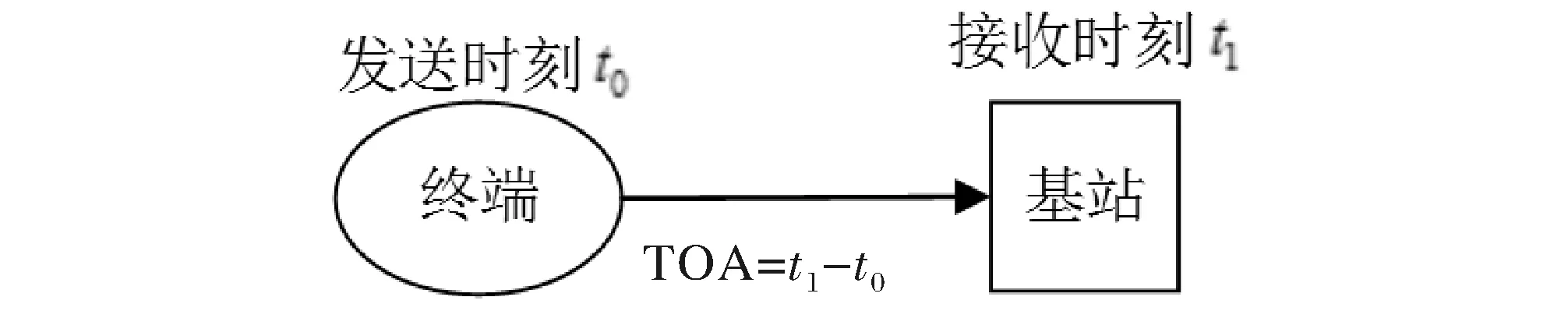
图2 TOA示意图

在不存在测量误差的理想情况下，(xi,yi,zi)假设为某个基站的坐标，(x,y,z)为手持终端的位置，定位方法的数学表达式可以表示为

(1)

其中，ri为所测的距离；di是手持终端和基站之间的实际距离。在理想情况下，di=ri。

当存在 NLOS 传播时， NLOS 误差在 TOA 定位方法中是一个正的附加延时超量，所以测得的终端到基站的距离就会大于终端到基站的实际距离。此时di0且≤1的误差因子。即终端位于以基站(xi,yi,zi)为圆心，ri为半径的圆圈内。 在视距传播时，ai= 1， 此时式(1)与式(2)相同

(2)

3 CHAN优化定位模型

为使定位的结果更加的精准,引入了粒子群算法与CHAN算法进行协同定位估计终端位置坐标。

3.1 基于粒子群的定位算法描述

在分析CHAN等定位算法的基础上，本文提出了基于粒子群优化及其改进的目标定位算法。使用的粒子群的基本核心是：将群体中每个飞行个体视为D维搜索空间中的一个点称之为粒子。粒子在空间搜索过程中按照一定的飞行速度，该速度根据粒子本身的飞行经验以及同伴的飞行经验进行动态调整，从而形成群体寻找最优值的反馈，这样会依据每个粒子对环境的适应度将个体逐步迁到较好的区域，并最终在搜索空间中寻找到研究问题的最优解[9]。将PSO算法应用在本文中，即将目标定位方程转换成优化求解的问题[10]。但是同样粒子群算法也存在着一定的局限性：由于缺乏局部精细搜索能力，算法在搜索后期容易陷入局部最优，出现收敛停滞现象。所以本文将在粒子群的基础上引入CHAN算法对一次定位结果加以修正。

图3 粒子群基本定位流程图

粒子群(PSO)算法描述：

步骤1 PSO算法先生成N个代表潜在问题解的粒子从而组成一个种群。设定种群规模为500，空间维数为3，迭代次数1 000、飞行速度范围及学习因子等参数。第i个粒子表示一个D维的向量，即：第i个粒子的位置是xi=[xi,1,xi,2,…,xi,D]T，(i=1,2,…,N) ；飞行速度是,vi=[vi,1,vi,2,…,vi,D]T,i=1,2,…,N

步骤2 计算每个粒子的适应度值，即使下式取得最小值

(3)

步骤3 计算当前每个粒子的适应度值，将此保存在pi中，pi=[pi,1,pi,2,…,pi,D]T,i=1,2,…,N将所有粒子的适应度值进行比较，群体中最优适应度值所代表的最优位置，保存在pg,pg=[pg,1,pg,2,…,pg,D]T,i=1,2,…,N; 种群中的粒子追随当前的最优粒子在目标搜索空间中，通过迭代方式搜索最优解；

步骤4 更新每个微粒的位置和速度

(4)

其中，c1和c2代表粒子个体和粒子群体的加速度权重系数；r1、r2分别代表与粒子个体及群体的加速度权重系数相关的随机初值；xi,j(t+1)，xi,j(t)，vi,j(t+1)，vi,j(t)分别表示第i个粒子在t+1和t时刻的位置和速度；

步骤5 计算所有基站与第 个终端的测试距离与实际距离之间的误差之和，然后更新粒子位置，从而使得误差最小，直至最终收敛于某个坐标；

步骤6 判断是否满足收敛条件，如果满足则继续进行；

步骤7 将最后全局最优个体输出，输出结果即为目标位置，运行结束。

3.2 基于CHAN算法描述

CHAN 算法是基于TOA 估计的定位算法，该算法采用最小二乘算法实现对终端位置的三维坐标估计，在噪声服从高斯分布的环境中，定位精度较高[11]。对于实际环境中因存在障碍物的影响而造成测量的时差存在较大误差的情况，该算法的精度将受到很大影响。

假定在三维空间中任意的分布着M个接收基站(BS)，待定位的手持终端(MS)坐标为(x,y,z)，已知第i个BS位置为(xi,yi,zi)和MS之间的距离为Ri，则根据测量得到的TOA 测量值τi可建立方程[12]

2Yiy-2Ziz+R=cτi,i=1,2,3,…,M

(4)

采用加权最小二乘法(WLS)，用TOA测量值的协方差矩阵Q近似代替误差ψ的协方差矩阵，可得

za=argmin{(h-Gaza)|Q-1(h-Gaza)|}=

(5)

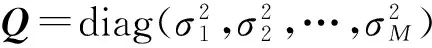
由于za中R实际上是与(x,y,z)有关的量，用Q矩阵近似代替误差矢量ψ的协方差矩阵也会带来一定误差。为得到更精确的估计位置，当TOA测量误差比较小时，M个TOA 测量值对应的误差矢量为

ψ=2Bn+n×n≈2Bn

(6)

3.3 粒子群/CHAN协同定位

鉴于在实际的定位系统中，测量数据的过程中会受到周围障碍物的随机干扰。考虑非视距(NLOS)误差对定位精度的影响，需要对基于 TOA 测量处理后的数据构建残差方程以进行分析，筛选出每个终端所对应的视距(LOS)情况下的基站，在只采用视距测量数据来定位终端的位置坐标，其定位精度将会有极大的改善[13-15]。

首先基于粒子群算法估算出位置信息，并通过对估计结果的残差计算均值，筛选出小于均值的以鉴别出NLOS与LOS所对应的基站坐标,从而滤除受到非视距环境影响的基站。其次，再对筛选出的符合条件的基站测量数据，利用CHAN方法二次计算出位置坐标。算法实现的基本描述：

步骤1 获取在 LOS 或 NLOS 环境下，某一终端和各个基站间的 TOA 测量值；

步骤2 利用粒子群算法初步估计移动终端的一次位置坐标估计；

步骤3 利用残差鉴别法对获取的 TOA 测量值进行数据分类，筛选出LOS环境下对应的基站；

步骤4 根据筛选出的LOS环境下的基站利用CHAN算法进行定位，来进一步提高终端坐标的定位精度；

步骤5 利用均值法对得出的结果进行验证。

4 实验结果与分析

结合仿真实验对算法的性能进行评估。测试数据来源于2016年全国研究生数学建模竞赛C题。

针对复杂环境下所采集的诸多的信号到达时间值，结合本文所提出的终端位置估计算法进行位置计算与定位。利用提出的基于粒子群与CHAN混合的定位算法模型，具体实现步骤入如下：

步骤1 在LOS或NLOS环境下，将与某一待定位终端通信的所有基站的TOA测量值，结合基站的坐标，利用粒子群算法首先估算出一次坐标值，再根据估计的坐标值与基站的坐标值，结合移动终端与基站之间的通信时间计算出通信距离，再利用提出的残差鉴别法进行 LOS 和 NLOS 数据分类；

步骤2 根据步骤1的分类结果，鉴别出相应的LOS和NLOS通信基站；

步骤3 由于NLOS环境下的TOA测量值包含较大的噪声，严重影定位算法的性能。因此，保留LOS环境下的定位基站，排除NLOS环境下的定位基站；

步骤4 根据步骤3保留的LOS环境下的基站,利用CHAN算法对待定终端的位置进行二次计算；

步骤5 输出待定位终端的位置坐标。

为检验文中提出的算法是否能有效抑制NLOS的干扰，结合粒子群算法、CHAN算法，以及本文所设计的混合定位算法，将最终得到的定位结果与5组终端原位置，分别计算其定位结果误差，并进行比较分析。结果如图4所示，基于粒子群算法的两次位置坐标估计值，以及与真实值之间的均方根差值。

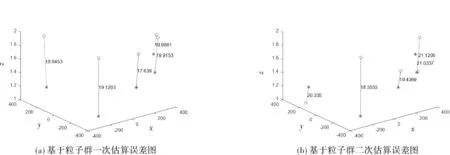
图4 基于粒子群的估算误差图

图5显示了基于CHAN算法的两次位置坐标估计值，分别于真实坐标之间的均方根差值。

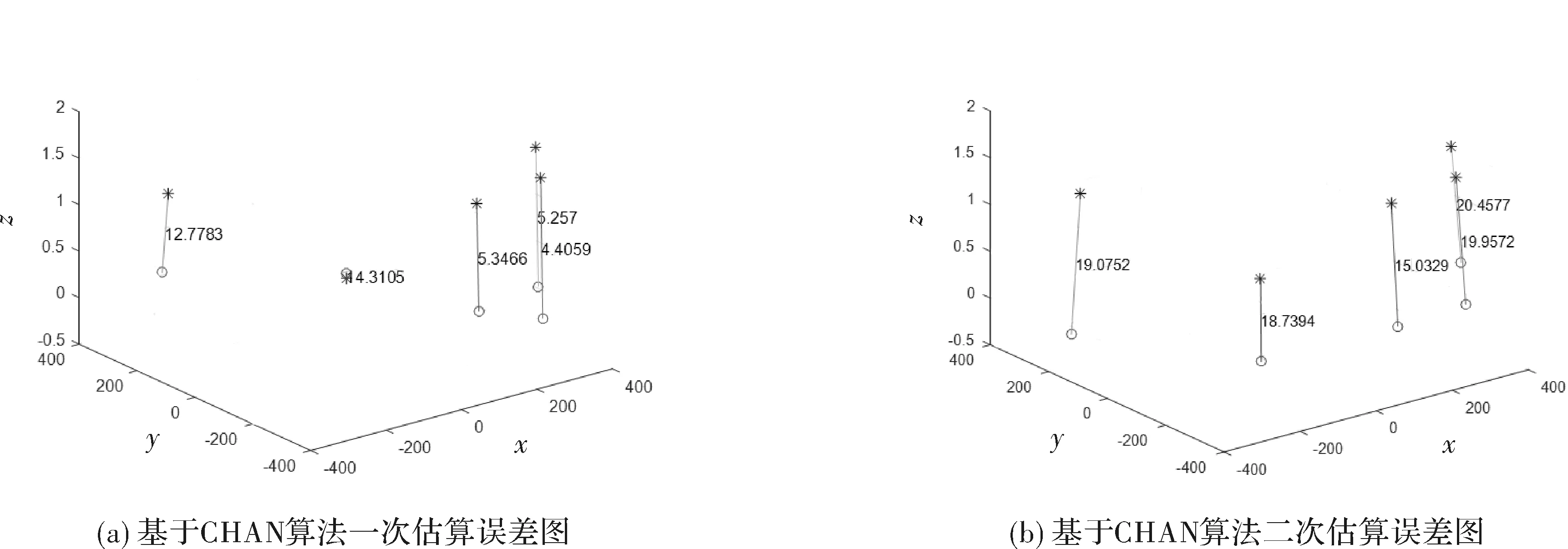
图5 基于CHAN算法的估算误差图

图6显示的为基于本文所提出的混合算法计算的差值。从图中能清楚的显示出基于本文所提出的混合算法在终端坐标估计精度上面有了较大提高。

通过3种方法得到的结果可以看出，基于混合的定位方法，其定位结果未出现较大的偏差，基本保持在较稳定的一个波动范围之内，波动幅度小，进一步证明了NLOS得到了有效的抑制。

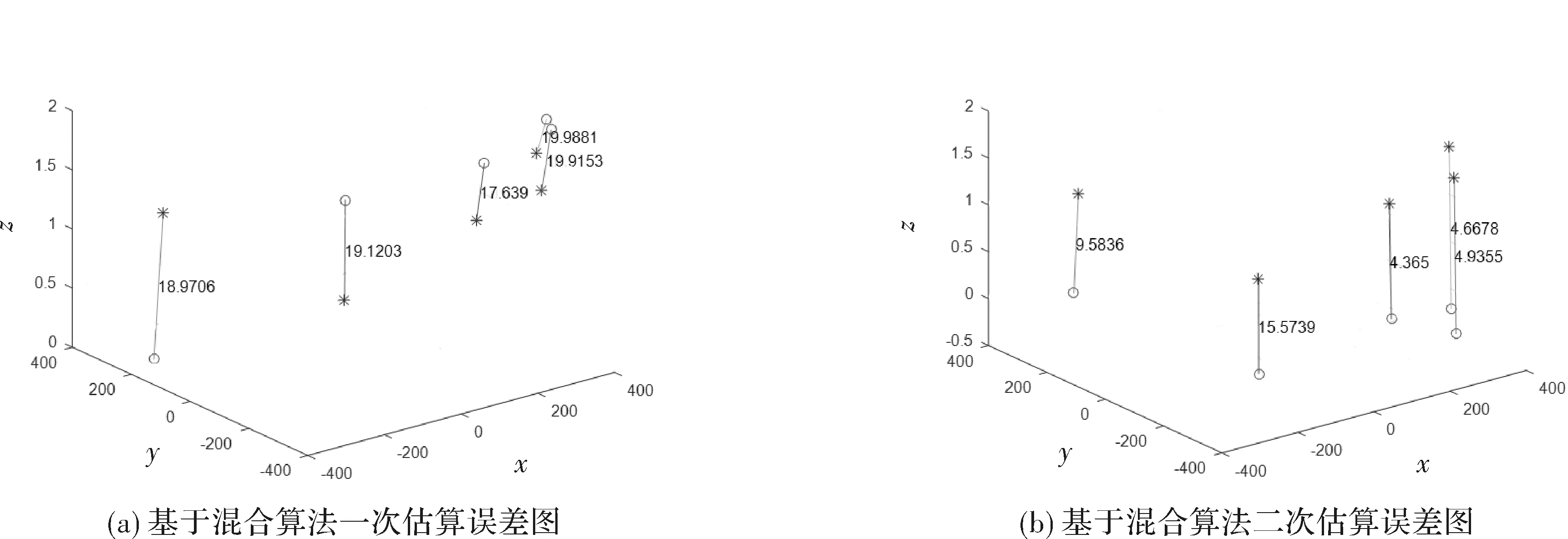
图6 基于混合算法的估算误差图

5 结束语

本文结合CHAN算法、粒子算法特点，改进现有的算法提出一种混合定位方法，通过时长计算和定位方程组求解完成移动终端节点的三维空间定位。对受NLOS污染严重的基站测量数据，通过筛选之后进行滤除，减少NLOS影响，提高定位精度等。通过对粒子群算法和CHAN算法进行综合优化，计算终端移动节点的坐标，解决移动终端在混合环境下的定位精度较低的问题。相比传统的定位算法，本文提出的方法在混合环境下能够较好的克服环境干扰因素的影响。实验结果表明，文中提出的混合定位方法能有效抑制室内环境下的NLOS干扰，具有较高的定位精度，具有良好的稳定性，在室内定位具有一定的实用价值。

[1] 王正.基于TDOA的无线传感器网络定位算法研究[D].南京:南京航空航天大学,2014.

[2] 宋玉,王洪雁.NLOS环境下基于到达时间差(TDOA)的定位算法[J].系统仿真技术,2006(3):125-129,143.

[3] 刘林.非视距环境下的无线定位算法及其性能分析[D].成都:西南交通大学,2007.

[4] 林国军.蜂窝网无线定位算法及其性能分析[D].成都:西南交通大学,2008.

[5] 邹杰,李珊君,陈晓明.一种改进的室内无线定位算法[J].计算机工程,2011(14):76-78.

[6] 沈郭浩,马永涛,刘开华,等.非视距环境下室内RFID标签定位算法研究[J].计算机工程与科学,2016(3):454-459.

[7] 王彪,傅忠谦.基于超宽带技术的TDOA室内三维定位算法研究[J].微型机与应用,2013(14):83-86.

[8] 姚金杰.基于地面基站的目标定位技术研究[D].太原:中北大学,2011.

[9] 罗平,向凤红,毛剑琳,等.基于自然选择的线性递减权重PSO与Taylor算法的TDOA协同定位算法研究[J].计算机应用研究,2014(4):1144-1146,1150.

[10] 潘烨炀.基于分布式传感器网络的地下浅层定位算法研究[D].太原:中北大学,2015.

[11] 陆音,王宝全,丘觐玮.CHAN算法在LOS和NLOS环境下的定位研究[J].计算机技术与发展,2015(9):61-65.

[12] Chan Y T,Ho K C.A simple and efficient estimator for hyperbolic location[J].IEEE Transactions on Signal Processing,1994,42(8):1905-1915.

[13] 郑飞,郑继禹.基于TDOA的CHAN算法在UWB系统LOS和NLOS环境中的应用研究[J]. 电子技术应用,2007(11):110-113,132.

[14] 段凯宇,张力军.一种在NLOS环境下提高精度的TDOA定位方法[J].南京邮电学院学报,2005,25(5):15-19.

[15] 常戎,吕善伟,张江林.提高NLOS环境下定位精度的TOA数据处理方法[J].北京航空航天大学学报,2006(8):946-949.

Research on Collaborative Localization Based on CHAN and Particle Swarm Optimization Algorithm

JIANG Feng,WU Fei,WANG Changzhi

(School of Electronic and Electrical Engineering，Shanghai University of Engineering Science，Shanghai 201600,China)

In view of the TOA positioning using CHAN algorithm, the accuracy of the positioning is affected by the environmental conditions greatly. Based on this, a method of cooperative localization based on particle swarm optimization and CHAN algorithm is proposed. Firstly, through particle swarm to estimate the mobile terminal using the initial solution, construction of initial solution residual equation, and screened under the environment of LOS corresponding to the base station, and the base station combined with CHAN positioning model was two times of mobile location final location estimation. The result showed that The positioning accuracy of the fusion algorithm based on the fusion algorithm is better than that of the single algorithm, and the positioning error is significantly reduced at least 5 meters.

location;CHAN algorithm;residual analysis method;particle swarm algorithm

2016- 10- 04

国家自然科学基金 (61272097)；上海市科委重点支撑项目 (13510501400)

江凤(1990-)，女，硕士研究生。研究方向：无线传感网络定位。吴飞(1968-)，男，博士，教授。研究方向：计算机并行处理与节能控制等。王昌志(1990-)，男，硕士研究生。研究方向：无线传感网络定位。

10.16180/j.cnki.issn1007-7820.2017.08.001

TN926+.3;TP306.1

A

1007-7820(2017)08-001-05