基于速度反馈与PID的电液比例位置系统特性仿真分析

王收军，杨静，郭津津

(1.天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.天津理工大学机械工程学院，天津 300384)

基于速度反馈与PID的电液比例位置系统特性仿真分析

王收军1,2，杨静1,2，郭津津1,2

(1.天津市先进机电系统设计与智能控制重点实验室，天津 300384；2.天津理工大学机械工程学院，天津 300384)

在建立的电液比例位置系统数学模型基础上,借用Matlab软件中的Simulink工具包对电液比例位置系统构建仿真模型,进行动态分析.结合实际生产要求,绘制Bode图验证建立系统的稳定性；利用速度反馈与PID控制,对位置系统的动态特性进行优化设计。仿真结果表明:速度反馈与PID结合的校正,使得位置系统超调量减小54.5%,响应时间减小0.62 s,稳态误差降低0.01 m;较正后系统的冲击消散,响应速度加快,响应更加平稳,控制精度得到提升,为系统的深层次优化提供依据。

电液比例位置控制；Simulink；速度反馈；PID控制

0 前言

电液比例位置系统是液压控制技术中的重要组成部分,在金属冶炼、工程机械和矿山机械等控制领域得到广泛应用，液压控制系统的动态特性是衡量其性能优劣的重要指标[1]。为了提高其特性,常采用PID控制以提升系统的快速性、准确性及稳定性。

Matlab是一种高效率的科学工程运算软件,它在解决系统仿真、信号处理、图像处理等方面功能强大。同时它所提供的Simulink工具包可以方便地对液压系统的动态特性进行仿真[2]。在实际工业过程中,由于被控对象建立的数学模型不精确,被控系统的非线性化或负载的变化,致使PID参数整定复杂化.通过分析建立电液比例位置系统的数学模型,以此作为仿真分析的依据与基础,利用Simulink工具包对系统进行仿真,结合速度反馈与PID控制,对系统的响应特性进行优化。

1 系统的组成及工作原理

电液比例位置系统原理如图1所示,系统主要由过滤器1、齿轮泵2、单向阀3、溢流阀4、蓄能器5、三位四通电液比例换向阀6、非对称液压缸7、位移传感器8、比例放大器9及负载滑块10等组成。

位置控制系统工作原理方框图如图2所示。系统通过控制软件给定一个输入信号(阶跃信号),位移传感器检测液压缸活塞杆输出的位移,经过A/D模数转换器转换为数字信号,与给定的输入信号进行比较,将比较的偏差值输入计算机,计算机控制系统根据偏差值计算出输出信号,再通过D/A数模转换器转换为电压信号,经过比例放大器的放大后转化成电流信号,由其控制三位四通电液比例换向阀阀芯的运动,从而控制液压缸内油液的输送,实现液压缸活塞杆的位置控制[3]。

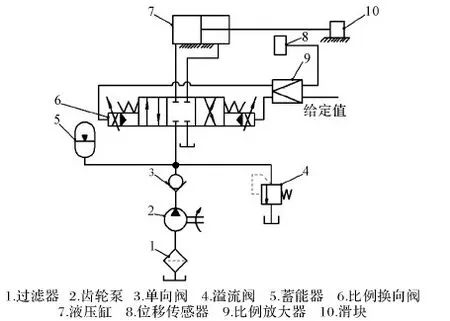
图1 电液比例位置系统

图2 位置控制系统框图

2 数学模型的建立

(1) 比例放大器的数学模型。经过计算机控制系统输出的数字信号通过D/A转换成模拟电压信号后输入到比例放大器中,比例放大器将输入的电压信号放大转变成电流信号,传输到比例电磁铁上,由于其转折频率比系统频宽高的多,可将其视为比例环节

(1)

式中，I(s)为比例放大器输出电流；Ka为比例放大系数；U(s)为比例放大器输入电压。

(2)三位四通电液比例阀的数学模型。工程上通常将电液比例方向阀视为一个二阶环节，故而它的二阶传递函数为

(2)

式中，ωv为电液比例阀固有频率；ξv为电液比例阀的阻尼比；Xv为阀芯位移。

(3) 液压缸的数学模型。根据电液比例阀阀口流量方程、非对称液压缸的流量连续方程、液压缸和负载的力学平衡方程,可以得到非对称缸数学模型

QL=KqXv-KcPL

(3)

(4)

AePL=ms2X+BsX+KX+F

(5)

由式(3)～(5)整理可得阀控缸在阀芯Xv和外负载力F同时输入时的活塞杆的位移X输出为

(6)

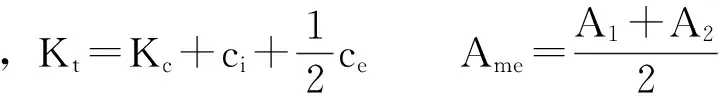
式中,kq、kc为流量增益及流量-压力系数；A1、A2为无杆腔与有杆腔面积；OL、PL为负载流量与负载压力；ce、ci为液压缸外、内泄漏系数；βe为油液有效体积弹性模量；m为活塞杆和负载折算活塞上的质量；B为粘性阻尼系数；k为负载弹簧刚度；V为液压缸体积；n为液压缸无杆腔与有杆腔面积之比；F为负载力。考虑到粘性阻尼系数B比较小,没有弹性负载存在(k=0),则式(3)可以化简为

(7)

综合式(1)、式(2)、式(7)可得电液比例位置系统的传递函数方框图如图3所示。

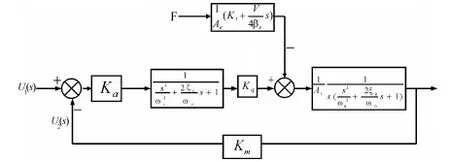
图3 位置控制系统传递函数框图

3 模型仿真分析

3.1 仿真模型

Matlab中的Simulink工具包能够对液压系统进行建模、仿真与分析,为使用者提供方框图进行模型连接,使系统模型建立简易化。考虑到电液比例位置系统数学模型的复杂性和实际仿真的要求,将其拆解为比例放大器、电液比例阀和阀控非对称缸三个子模型,依据子模型从Simulink中取得阶跃信号模块与增益模块、传递函数模块与微分模块、常数模块与示波器建立对应的仿真模型,根据电液比例位置系统的传递函数方框图,将各子模型的输入、输出口依次对应相连,即可得到系统的整体仿真模型如图4所示，利用该仿真模型可以对电液比例位置系统进行动态仿真分析与优化。

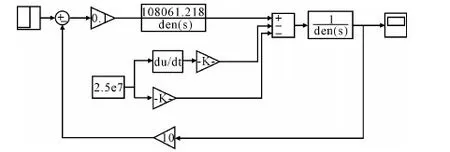
图4 系统仿真模型

在仿真模型中控制系统各参数的取值如表1所示。

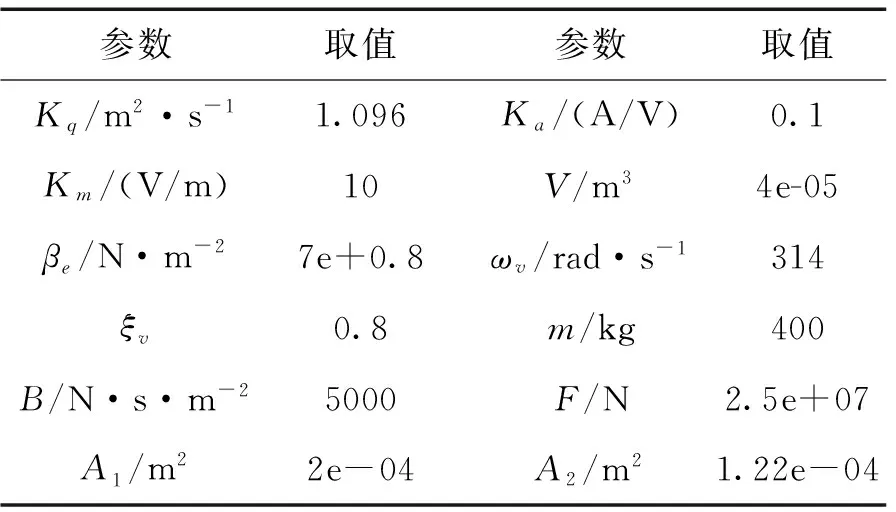
表1 仿真参数

将表1中的系统参数代入到传递函数中,借用Matlab软件编写程序,能够绘制开环系统Bode图,如图5所示。

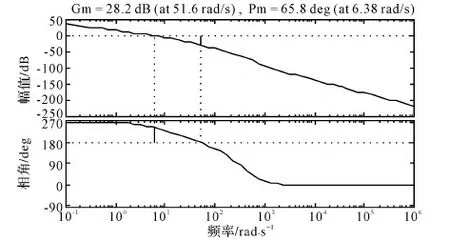
图5 开环系统Bode图

根据Bode图,可知此时系统相位裕度γ为65.8°,幅值裕度kg为28.2 dB,系统是相对稳定的,满足工程实践的要求。

3.2 仿真结果与分析

瞬态响应是对电液比例位置系统动态性能评价的重要指标,响应曲线可以很直观的反应系统动态性能的优劣。为了能够清晰的观测电液比例位置系统的输出响应,在Simulink界面中对阶跃信号进行仿真,基于图3仿真模型,选用刚性系统的ode23tb求解器和变步长对系统进行动态仿真和分析,仿真时间设定为1.5 s,得到的系统阶跃响应如图6所示。

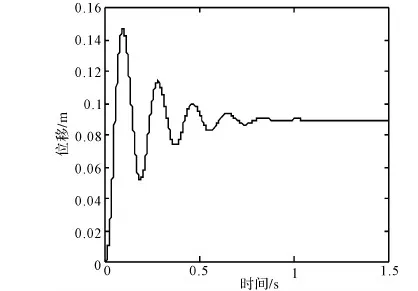
图6 阶跃响应曲线

从瞬态响应曲线可以看出:电液比例位置系

统在单位阶跃输入下,系统的最大超调量达到54.5%,上升时间为0.06 s,振荡次数较多,直到0.94 s才完全平稳,稳态误差达到0.01 m。由此可知,过大的超调量将会对电液比例位置系统造成冲击,振荡次数过多易引起系统液压元件的共振,响应时间过长致使系统的快速性减小,稳态误差过大会使系统的控制精度降低,无法满足实际工程要求,需要对系统进行分析并引入校正装置来优化系统的动态特性。

3.3 仿真校正

3.3.1 速度反馈校正

在伺服系统中,速度反馈以其良好的平稳性与快速性得到广泛的应用。速度反馈是负载有运动时才有反馈信号,负载位移稳定时没有反馈作用,所以系统具有很高的静态刚度。在电液比例位置系统的基础上引入速度反馈,即将活塞杆位移的微分引入控制系统。微分环节的引入使得系统相位超前,不仅可以提高液压缸的响应速度,进而减小稳态误差,而且补偿系统过大的相角滞后,增加系统的相角稳定裕度,从而提高系统的稳定性[4]。引入速度反馈校正的系统工作原理如图7所示。

图7 速度反馈校正的系统框图

速度校正前与速度校正后的阶跃响应对比如图8所示。

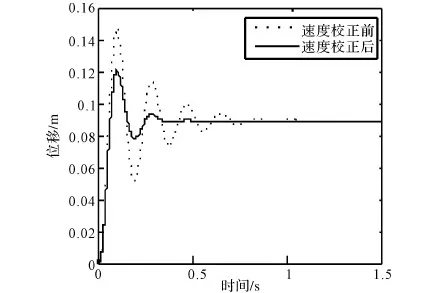
图8 速度校正前后的阶跃响应

从瞬态响应曲线可以看出:速度校正后系统瞬态响应的最大超调量减小32.3%、振荡次数明显减小、上升时间减小0.009 s、响应时间减小0.38 s、稳态误差减小0.0015 m;校正后的系统冲击将会降低,系统响应的快速性与稳定性有所提高,准确性则需要进一步优化。通过速度反馈的引入,使得主回路的静态刚度得到提高,减少速度反馈回路内电液比例阀滞环、温漂的干扰和非线性影响,提升位置系统的静态精度[5]。

3.3.2 PID控制校正

对电液比例位置系统的校正除速度反馈外仍有多种方式,PID以其算法简单、鲁棒性好、可靠性高而成为校正的主要技术。在电液比例位置系统的基础上引入PID控制,将活塞杆位移输出量与给定量的偏差输送到计算机设定的PID控制算式,将偏差按比例、积分、微分通过线性组合构成控制量对被控对象进行控制，引入PID控制校正的系统工作原理如图9所示。

图9 PID控制校正的系统框图

系统引入PID控制算法,选择临界比例度原则和经验试凑法对控制系统进行设计分析,确定比例、积分、微分的控制参数。在引入控制算法的控制系统中,采用纯比例控制(Ti=∞,Td=0),增加比例系数,直到系统开始出现等幅震荡,记录此时的临界比例系数Ku和临界震荡周期Tu,按照Kp=0.6Ku,Ki=1.2Ku/Tu,Kd=0.072KuTu计算三个参数值,与凑试法相结合确定Kp=2.5,Ki=1,Kd=0.15,得到的速度反馈和PID校正阶跃响应对比如图10所示。

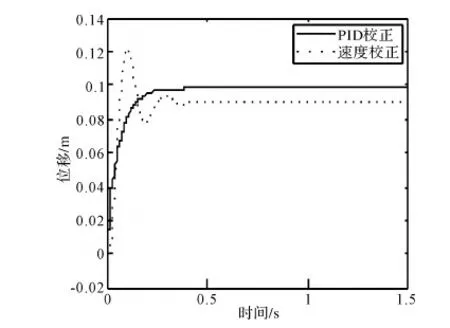
图10 速度校正和PID校正的阶跃响应对比

从瞬态响应曲线可以看出:通过PID校正和速度反馈校正的对比,可以很清晰的看到位置系统的超调量减小22.2%,振荡次数降低,延迟时间降低0.003 s,调整时间减小0.07 s,稳态误差减小0.0077 m;PID校正的引入使得系统的动态特性得到优化,系统冲击完全消散,响应的快速性、稳定性得到很大的提升,但准确性仍需进行校正。

3.3.3 速度反馈与PID相结合校正

为使电液比例位置系统的动态特性得到进一步优化,将速度反馈与PID校正相结合。利用速度反馈校正,使得位置系统固有频率增大,但是阻尼比下降,开环放大系数会减小;引入PID校正环节,可以对速度反馈中开环放大系数进行补偿,对阻尼系数进行校正,使得整个系统的快速性、准确性、稳定性得到优化。PID校正与联合校正的阶跃响应对比如图11所示。

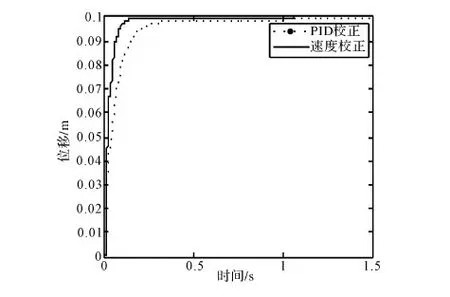
图11 PID校正和联合校正的阶跃响应对比

从瞬态响应曲线可以看出:电液比例位置系统调整时间降低0.17 s,稳态误差减小0.001 m;通过联合校正,系统瞬态响应的快速性、准确性与稳定性得到进一步提高。很明显,加入速度反馈的PID校正比单一的PID校正效果要好很多,速度反馈的引入,使得电液比例阀、非对称缸传递环节构成闭环回路,减小回路内的干扰和非线性的影响,PID参数的整定变得简易,响应更加平稳,系统的动、静态特性得到极大程度的优化,可以满足工程实践的要求。

4 结论

(1)在考虑阀控缸非线性特性的条件下,推导出比例放大器、电液比例阀与阀控非对称缸的传递函数,建立电液比例位置系统的数学模型,构建传递函数方框图,为液压系统仿真模型的建立奠定理论基础。

(2)在恒定负载力的作用下,建立系统仿真模型,通过速度反馈、PID调节、速度反馈与PID调节相结合的瞬态响应对比,可以很明显的看出速度反馈与PID相结合的调节使电液比例位置系统的快速性、稳定性、准确性得到提升,使系统具备良好的动、静态品质。

[1] 郭兵, 鲁植雄. 基于AMESim和MATLAB的拖拉机电控液压悬挂系统仿真[J]. 农机化研究, 2014(01):36-39.

[2] 游张平, 王卫锋. 基于SIMULINK的液压伺服系统动态仿真[J]. 中国工程机械学报, 2004(01):47-49.

[3] 吴远会. 对称阀控制非对称缸电液伺服系统建模分析[J]. 设计技术, 2011(02):24-29.

[4] 谢国庆,周晓明,金梁斌. 基于AMESim的电液位置控制系统动态性能仿真分析及优化[J].机床与液压,2014(04):47-49.

[5] 于洋. 液压系统的污染与控制[J]. 科技转让集锦, 2011(11):138-138.

Simulation analysis of electro hydraulic proportional position system based onthe speed of feedback and PID

WANG Shou-jun1,2，YANG Jing1,2，GUO Jin-jin1,2

(1.Advanced Mechanical and Electrical System Design in Tianjin and Key Laboratory of Intelligent Control， Tianjin 300384，China; 2. College of Mechanical Engineering, Tianjin University of Technology, Tianjin 300384, China)

Based on the mathematical model of the electro-hydraulic proportional position system, a simulation model of electro-hydraulic proportional position system was built by using the Simulink tool in Matlab software, and the dynamic analysis was carried out. According to the actual production requirements, Bode chart was drawn to verify the stability of the system. Using of speed feedback and PID control, the dynamic characteristics of the position system were optimized and designed. The simulation results show that the overshoot of the position system decrease 54.5%, and the response time is reduced by 0.62 s, the steady state error is reduced by 0.01m through adjusting of combine velocity feedback and PID. After the system was adjusted, its impact was dissipation, the response speed was more stable and fast, the control precision was higher, which provides the basis for the deep level optimization of the system.

electro-hydraulic proportional position control；Simulink；speed feedback；PID control

2016-09-23；

2016-11-18

天津市高等学校科技发展基金计划项目(20120705)

王收军(1965-)，男，河北人，机械学院院长，教授，硕士，主要研究方向为机电液一体化成套设备及单元技术和流体传动及控制技术。

杨静(1989-)，男，硕士研究生，研究方向为流体传动与控制。

TH137.5

A

1001-196X(2017)03-0058-06