基于无滤波器方波信号注入的永磁同步电机初始位置检测方法

张国强 王高林 徐殿国

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

基于无滤波器方波信号注入的永磁同步电机初始位置检测方法

张国强 王高林 徐殿国

（哈尔滨工业大学电气工程及自动化学院 哈尔滨 150001）

针对无位置传感器内置式永磁同步电机（IPMSM）初始位置检测中，传统的基于凸极跟踪的短脉冲电压注入法难以确定脉冲宽度和幅值、实现困难、二次谐波分量法信噪比低的缺点，提出一种基于无滤波器方波信号注入的IPMSM初始位置检测方法。首先通过向观测的转子d轴注入高频方波电压信号，采用无滤波器载波信号分离方法解耦位置误差信息，通过位置跟踪器获取磁极位置初定值；然后基于磁饱和效应，通过施加方向相反的d轴电流偏置给定，比较d轴高频电流响应幅值大小实现磁极极性辨识；最后，通过2.2kW IPMSM矢量控制系统对提出的基于无滤波器方波信号注入的初始位置检测方法进行实验验证。结果表明，所提方法收敛速度较快，可在IPMSM转子静止或自由运行状态实现初始位置辨识和低速可靠运行，位置观测误差最大值为6.9°。

内置式永磁同步电机 无位置传感器 无滤波器 方波注入 初始位置检测

0 引言

内置式永磁同步电机（Interior Permanent Magnet Synchronous Machine, IPMSM）具有高功率密度、高转矩电流比的特点，已经广泛应用于工业现场、电动汽车、家用电器等领域[1]。无位置传感器控制技术能够有效减小系统体积和成本，增加系统可靠性，并能够在高温、高湿等恶劣环境场合应用，已成为当今研究热点[2-11]。根据转速适用范围不同，无位置传感器PMSM控制技术主要可分为两类：一类适用于中高速运行，主要利用基频激励的反电动势或者磁链信息进行转子位置估计，即模型法[2-5]；另一类适用于低速（零速）运行，主要利用电极凸极特性获取转子位置信息，即凸极跟踪法[6-11]，该方法能够有效观测转子位置，却不能实现磁极极性辨识。

在无位置传感器PMSM矢量控制系统中，电机所产生的最大起动转矩与磁极初始位置的准确辨识程度有关。如果磁极初始位置误差过大，那么电机带载能力受到限制，甚至出现反转现象，极端情况下会导致起动失败。因此，对于高性能无位置传感器PMSM矢量控制系统，转子初始位置的准确辨识极为重要。

目前，已有多种PMSM转子初始位置估计方法相继被提出[8-12]。其中，比较典型的方法是首先利用基于凸极追踪的方法（高频信号注入法）观测转子位置，然后利用短脉冲电压注入法或二次谐波分量法辨识磁极极性[10,11]。文献[10]采用一种基于混合信号注入的IPMSM改进转子磁极初始位置估计方法，通过注入高频旋转电压信号的方法检测磁极位置；以磁极位置初定值为矢量角，采用短脉冲注入法，往定子绕组注入两个方向相反的脉冲电压矢量，通过比较激励的d轴电流大小可以简单、有效地判断出磁极极性。该方法鲁棒性较强，然而短脉冲注入法难以确定脉冲宽度和幅值、实现困难；且该方法是独立于高频注入法磁极位置估计的辨识过程，使得高频注入法被迫中断、无持续性，因此该方法无法实现自由运行条件下初始位置检测。文献[11]利用包含转子位置信息的高频响应电流二次谐波分量实现磁极极性辨识，然而二次谐波分量信噪比较低、算法较为复杂，对硬件要求较高，且鲁棒性较差。采用正弦信号注入（旋转矢量或脉振矢量）的方法需要采用滤波环节实现载波信号分离与提取，因此算法收敛速度较慢。文献[12]提出一种基于磁路饱和效应的电压脉冲注入法，通过检测不同角度差脉冲电压矢量注入时因磁路饱和程度不一致产生的电流响应实现初始位置辨识。然而，在实际应用中，该方案受电流采样电路精度和干扰影响，位置辨识准确性受到限制。

本文提出一种基于无滤波器方波信号注入的IPMSM转子初始位置检测方法。首先通过向观测的转子d轴注入方波电压信号，采用无滤波器载波信号分离方法解耦位置误差信号，通过位置跟踪器获取磁极位置初定值；然后改变d轴电流偏置给定方向，通过比较d轴高频电流响应幅值大小实现磁极极性辨识；最后，通过2.2kW IPMSM矢量控制系统对所提出的基于无滤波器方波信号注入的初始位置检测方法进行实验验证。

1 基于无滤波器方波注入的磁极位置辨识

1.1 方波电压注入磁极位置辨识方法

图1为基于无滤波器方波电压信号注入的IPMSM磁极位置辨识原理框图。在观测的转子d轴注入脉

图1 基于无滤波器方波信号注入的磁极位置辨识Fig.1 Magnetic pole position estimaiton based on filterless square-wave injection

IPMSM在同步dq坐标系下的数学模型为

式中，ud、uq和id、iq分别为IPMSM d、q轴下电压和电流分量；R为定子电阻；Ld、Lq分别为d、q轴电感；Ψf为永磁体磁链；ωe为转子电角速度；p为微分算子。

由于注入方波电压信号频率远大于基波运行频率，因此忽略定子电阻压降和反电动势影响，IPMSM在高频信号激励下可等效为感性负载，有

将式（2）变换到静止αβ 坐标系，得到高频电流响应为

式中，αhi、βhi分别为α、β 轴下高频响应电流分量。在观测的转子d轴注入对称方波电压信号

因此可得静止αβ 坐标系下的高频响应电流信号包络为

式中，Iαh、Iβh分别为静止α、β 轴下的高频响应电流包络；ωh为注入方波电压信号频率；Lavg= (Ld+Lq)2为电感均值；Ldif=(Ld-Lq)2为电感差值。

可见，Iαh、Iβh中包含转子位置信息，但前提是Ld≠Lq，即电机存在凸极效应。

当位置跟踪器收敛时，即Δθe=0，有

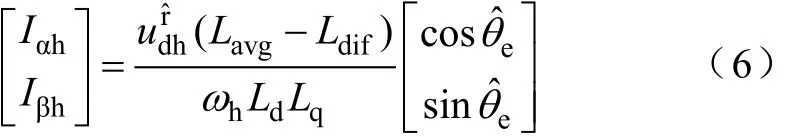
因此，通过包络检测器提取Iαh、Iβh后，可直接采用反正切函数计算跟踪转子位置信息。

然而，反正切函数计算对αhI、βhI噪声比较敏感，鲁棒性较差。因此，本文采用矢量叉乘方法解耦位置误差信息，其原理如图2所示。并通过基于IPMSM机械模型的PID类型Luenberger位置跟踪器观测转子位置信息，其原理框图如图3所示，其中P为极对数。

图2 位置误差信号解耦Fig.2 Demodulation of the position error signal

图3 Luenberger位置跟踪器Fig.3 Luenberger based position tracking observer

Luenberger位置跟踪器闭环传递函数为

式中，J、ˆJ分别为转动惯量及其观测值；kp、ki、kd分别为Luenberger位置跟踪器比例、积分、微分增益。可见，通过Luenberger位置跟踪器，能够实现转子位置零相位滞后准确辨识。

1.2 无滤波器载波信号分离策略

通常情况下，需要采用带阻滤波器（包括低通滤波器或者陷波滤波器等）实现载波信号分离，进而构成电流闭环；采用带通滤波器提取载波信号，进而解耦出位置偏差信息。然而，滤波器环节的采用限制了系统带宽，降低了位置观测响应速度；并且高阶滤波器的应用会占用较多系统资源。因此，本文研究一种无滤波器载波信号分离策略。

图4为注入方波电压信号频率与PWM载波信号频率相等时，同步dq坐标系下注入高频电压信号和响应电流信号时序图[7]。由于注入方波信号频率远高于基波运行频率，因此，在相邻采样时刻可认为基波电流信号保持恒定；因为注入方波电压信号具有正负半周对称形式，因此，在相邻两个采样时刻，高频响应电流信号幅值相等。通过上述分析，可知在不同采样时刻，高频响应电流可表示为

式中，idqh(k )、idqs(k )、idqf(k)分别为k采样时刻高频响应电流矢量、采样电流矢量和基波电流矢量；下标s表示采样信号；下标f表示基波信号。

图4 注入高频电压信号和响应电流信号的时序图Fig.4 Timing sequence of the injected square-wave voltage vector and the high-frequency current response

通过简单代数运算实现无滤波器载波信号分离，其原理框图如图5所示。采用无滤波器载波信号分离策略，代替传统的带阻滤波器和带通滤波器，能够有效减小资源占用，并提高系统带宽，加快位置观测策略收敛时间。

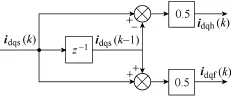
图5 无滤波器载波信号的分离Fig.5 Filterless carrier signal speration

2 磁极极性辨识

通过无滤波器方波电压信号注入法可以获得转子位置信息，然而却不能实现磁极极性（N极或S极）辨识。因此，即使注入方波电压矢量出现在负向观测转子d轴，观测器依然收敛。为实现转子磁极极性辨识，传统方法是在观测转子d轴注入短脉冲电压或者通过包含转子位置信息的高频响应电流二次谐波分量用于磁极极性辨识。然而，短脉冲电压注入方法难于确定脉冲宽度和幅值、实现困难，且是独立于基于无滤波器方波注入的磁极位置辨识的过程；而基于高频响应电流二次谐波分量的方法由于信噪比问题降低了位置辨识精度。本文利用磁路的饱和效应，在无滤波器方波注入磁极位置辨识后，仅改变d轴电流偏置给定方向，通过比较d轴高频电流响应幅值大小完成磁极极性辨识，实现较为简单。

磁路饱和效应及高频电流响应如图6所示[9]。当d轴直流偏置给定与转子磁极极性相同时（A点），定子磁通Ψd饱和程度增强，增量电感减小，d轴高频响应电流幅值增大；相反，当d轴直流偏置给定与转子磁极极性相反时（B点），定子磁通饱和程度减弱，增量电感增大，d轴高频响应电流幅值减小。通过比较正负d轴电流偏置给定±下所激励

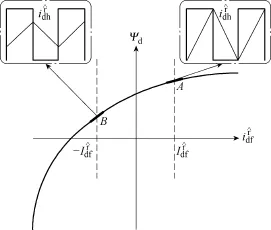
图6 磁饱和效应及高频电流响应Fig.6 Magnetic saturation effect and induced HF current

d轴高频电流幅值大小，即可实现转子磁极极性辨

识。图7为转子磁极辨识原理框图。若irˆ(I*)＞

dhdf

-irˆ(I*)，则无滤波器方波电压信号注入法所得位

dhdf

置即为转子N极；反之，若iˆr(I*)＜-irˆ(I*)，

dhdfdhdf

则无滤波器方波电压信号注入法所得位置即为转子S极，需要进行角度补偿，补偿值为π。在实际应用过程中，在±Id*f给定中间，令基波电流给定为0使其恢复初始状态。此外，为保证磁极极性辨识策略可靠性，在±Id*f给定且稳定收敛后，累积d轴高频响应电流幅值作为磁极辨识依据，在本文中累积数据点为10。

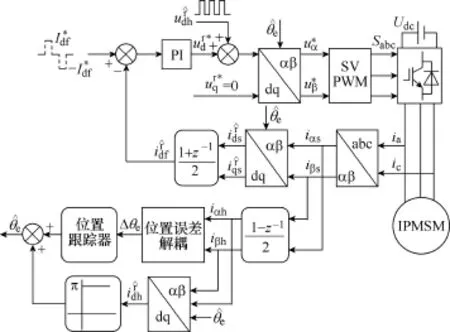
图7 转子磁极极性辨识Fig.7 Magnetic polarity detection

3 实验结果分析

为验证基于无滤波器方波信号注入的转子初始位置辨识策略有效性，本文在2.2kW无位置传感器IPMSM矢量控制平台进行研究。IPMSM参数见表1。采用STM32F103VCT6 ARM芯片实现控制算法，通过绝对式编码器ECN-1113对转子实际位置和转速进行检测，仅用于与观测结果进行比较。PWM开关频率为2kHz，采用双采样双更新模式，电流环带宽为200Hz，方波电压注入幅值为120V，频率为2kHz，d轴电流偏置给定幅值为3A。采用无传感器混合控制策略进行实验。

表1 IPMSM参数Tab.1 Parameters of the tested IPMSM

图8为IPMSM转子固定在72°位置时，采用本文所提基于无滤波器方波信号注入的初始位置检测实验结果。可见，整个初始位置辨识过程耗时50ms，其中磁极位置辨识时间为20ms，正负及零d轴偏置给定时间分别为10ms，基于无滤波器方波注入磁极位置收敛时间约为5ms。图8a为磁极位置收敛到N极实验结果，位置观测误差为2.5°；图8b

图8 静止条件下的初始位置检测Fig.8 Initial position detection at standstill

图9为IPMSM转子自由运行条件下，采用本文所提基于无滤波器方波信号注入的初始位置检测实验结果。图9a为磁极位置收敛到N极实验结果，图9b为图9a中虚线内的局部放大结果，位置观测误差为-1.8°；图9c为磁极位置收敛到S极实验结果；图9d为图9c中虚线内的局部放大结果，位置观测误差为1.4°。可见，本文提出的基于无滤波器方波信号注入初始位置检测具有较快的收敛速度，对于转子静止状态和自由运行状态，均能有效辨识IPMSM初始位置。

图9 自由运行下初始位置检测Fig.9 Initial position detection in free-running mode

图10为IPMSM转子在一个电角度周期内不同位置时的初始位置辨识结果。可以看出，本文所提初始位置检测策略辨识效果较好，最大观测误差为6.9°。根据IPMSM矢量控制方式下的转矩方程式，在所述允许的观测误差范围内可以产生足够的起动转矩，能够满足无位置传感器IPMSM的起动要求。

图11为IPMSM在任意位置起动至100r/min的实验结果。可见，采用本文所提基于无滤波器方波信号注入的初始位置检测方法，观测位置、转速能够较快收敛到其实际值。IPMSM在起动过程中不会发生反转或抖动现象，且能够实现低速可靠运行，证明了该方法对IPMSM初始位置检测的有效性，并具有较好的应用价值。

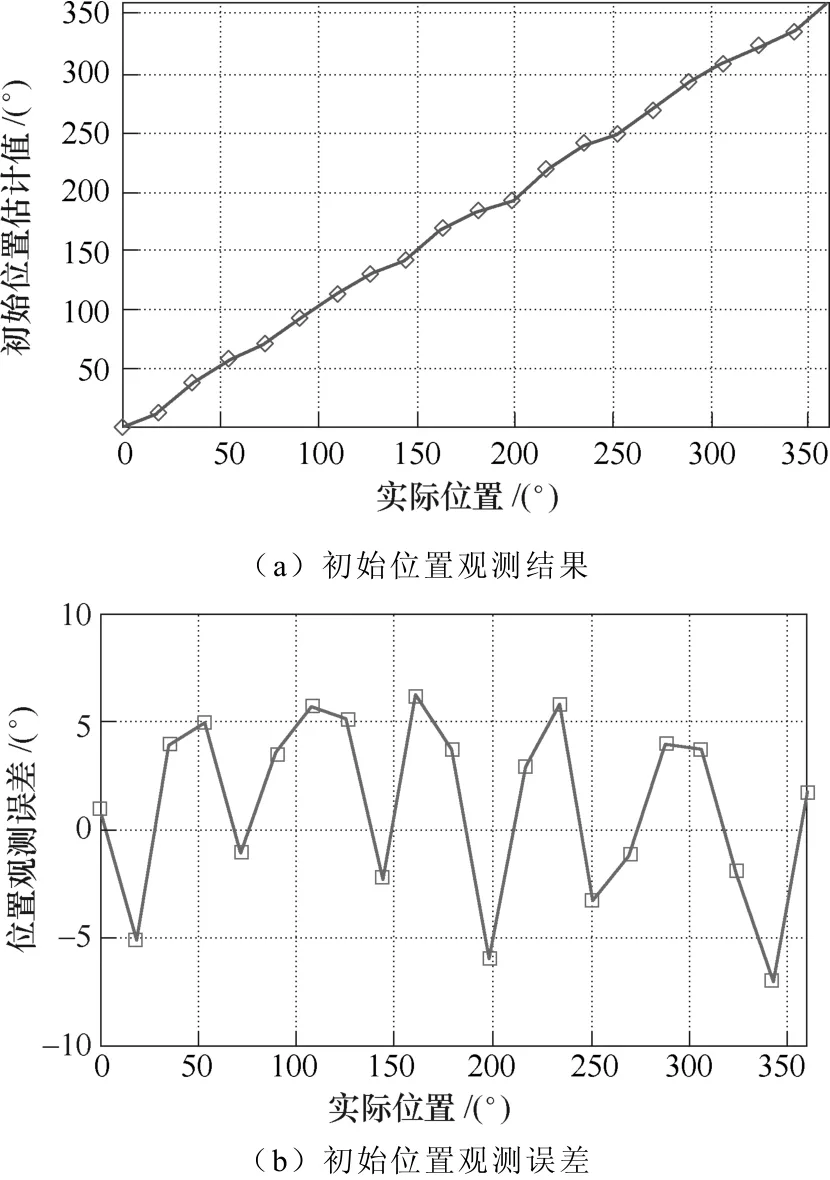
图10 初始位置检测统计结果Fig.10 Initial position detection statistical results

图11 IPMSM起动实验Fig.11 Startup operation of IPMSM

4 结论

本文提出了一种基于无滤波器方波信号注入的IPMSM初始位置检测方法。通过向观测的转子d轴注入高频方波电压信号，采用无滤波器载波信号分离方法解耦位置误差信息，提高了算法收敛速度。通过比较施加方向相反d轴电流偏置给定时d轴高频电流响应幅值大小，实现磁极极性辨识。实验结果表明，所提基于无滤波器方波信号注入的初始位置检测方法收敛速度较快，能够在IPMSM转子静止或自由运行状态实现初始位置辨识，位置观测误差最大值为6.9°。

[1] Kwon Y C, Sul S K, Baloch N A, et al. Improved design of IPMSM for sensorless drive with absolute rotor position estimation capability[J]. IEEE Transactions on Industry Applications, 2016, 52(2)： 1441-1451.

[2] 张国强, 王高林, 倪荣刚, 等. 基于自适应线性神经元滤波的内置式永磁电机转子位置观测器[J].电工技术学报, 2016, 31(6)： 83-89. Zhang Guoqiang, Wang Gaolin, Ni Ronggang, et al. Adaptive linear element filtering based rotor position observer for interior permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2016, 31(6)： 83-89.

[3] Bolognani S, Calligaro S, Petrella R. Design issues and estimation errors analysis of back-EMF-based position and speed observer for SPM synchronous motors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2014, 2(2)： 159-170.

[4] 李冉, 赵光宙, 徐绍娟. 基于扩展滑模观测器的永磁同步电动机无传感器控制[J]. 电工技术学报, 2012, 27(3)： 79-85. Li Ran, Zhao Guangzhou, Xu Shaojuan. Sensorless control of permanent magnet synchronous motor based on extended sliding mode observer[J]. Transactions of China Electrotechnical Society, 2012, 27(3)：79-85.

[5] 陆婋泉, 林鹤云, 冯奕, 等. 永磁同步电机无传感器控制的软开关滑模观测器[J]. 电工技术学报, 2015, 30(2)： 106-113. Lu xiaoquan, Lin Heyun, Feng Yi, et al. Soft switching sliding mode observer for PMSM sensorless control[J]. Transactions of China Electrotechnical Society, 2015, 30(2)： 106-113.

[6] Yoon Y D, Sul S K, Shinya M, et al. High-bandwidth sensorless algorithm for AC machines based on square-wave-type voltage injection[J]. IEEE Transactions on Industry Applications, 2011, 47(3)： 1361-1370.

[7] Park N C, Kim S H. Simple sensorless algorithm for interior permanent magnet synchronous motors based on high-frequency voltage injection method[J]. IET Electric Power Applications, 2014, 8(2)： 68-75.

[8] Gong L M, Zhu Z Q. Robust initial rotor position estimation of permanent-magnet brushless AC machines with carrier-signal-injection-based sensorless control[J]. IEEE Transactions on Industry Applications, 2013, 49(6)： 2602-2609.

[9] Suzuki T, Hasegawa M, Tomita M. Fast initial position estimation of IPMSMs using comb filters[J]. IEEJ Journal of Industry Applications, 2014, 3(2)：104-111.

[10] 王高林, 杨荣峰, 于泳, 等. 内置式永磁同步电机转子初始位置估计方法[J]. 电机与控制学报, 2010, 14(6)： 56-60. Wang Gaolin, Yang Rongfeng, Yu Yong, et al. Initial rotor position estimation for interior permanent magnet synchronous motor[J]. Electrical Machines and Control, 2010, 14(6)： 56-60.

[11] Raca D, Harke M C, Lorenz R D. Robust magnet polarity estimation for initialization of PM synchronous machines with near-zero saliency[J]. IEEE Transactions on Industry Applications, 2008, 44(4)： 1199-1209.

[12] 蒯松岩, 王鹏飞, 黄玉龙. 基于简化电感模型全域SRM无位置传感器研究[J]. 电机与控制学报, 2013, 28(8)： 1-8. Kuai Songyan, Wang Pengfei, Huang Yulong. The global position sensorless technology of switched reluctance motor based on the simple inductance mode[J]. Electric Machines and Control, 2013, 28(8)： 1-8.

（编辑 张玉荣）

Filterless Square-Wave Injection Based Initial Position Detection for Permanent Magnet Synchronous Machines

Zhang Guoqiang Wang Gaolin Xu Dianguo
（School of Electrical Engineering and Automation Harbin Institute of Technology Harbin 150001 China）

With regard to the initial position detection for position sensorless interior permanent magnet synchronous machine (IPMSM) drives, existing saliency-tracking-based methods have difficulties to determine the amplitude and width of the pulses for the short pulses injection method, and also have low signal-noise ratio for the position-dependent secondary-harmonics-based method. Hence, this paper presents a filterless square-wave voltage injection based initial position detection scheme for position sensorless IPMSM drives. A high-frequency square-wave voltage vector is injected in the estimated d-axis, then the position error information is demodulated through filterless carrier signal separation, and the position tracking observer is adopted to obtain the initial position. Based on the magnetic saturation effect, the magnetic polarity can be identified by comparing the amplitudes of the induced d-axis high-frequency current with two given d-axis current offsets which are equal in value but opposite in direction. Experiments on a 2.2kW IPMSM sensorless vector controlled drive have been carried out to verify the proposed scheme. The experimental results show that the initial position detection for standstill and free-running rotor applications as well as the stable operation atlow speed range can be guaranteed with a fast convergence speed. The maximum position estimation error is limited within 6.9°.

Interior permanent magnet synchronous machine, position sensorless, filterless, square-wave injection, initial position detection

TM351

张国强 男，1987年生，博士，研究方向为永磁同步电机无位置传感器控制技术。

E-mail： wisdom9527@163.com（通信作者）

王高林 男，1978年生，教授，博士生导师，研究方向为交流电机控制理论与应用技术。

E-mail： wgl818@hit.edu.cn

10.19595/j.cnki.1000-6753.tces.L70030

国家自然科学基金（51522701）和台达环境与教育基金会电力电子科教发展计划（DREK2015002）资助项目。

2016-07-14 改稿日期 2016-12-09