电磁发射用多级混合储能充电策略优化

李 超 鲁军勇 马伟明 江汉红 龙鑫林

（海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033）

电磁发射用多级混合储能充电策略优化

李 超 鲁军勇 马伟明 江汉红 龙鑫林

（海军工程大学舰船综合电力技术国防科技重点实验室 武汉 430033）

时序串联充电策略用多组蓄电池并联来满足功率需求，过高的并联数使系统体积、重量过于庞大不利于工程化。本文在普通时序串联电容充电方法基础上，提出一种快速充电优化方案，能够在保证充电速度的前提下降低并联数。首先并联电池组对电容充电，之后通过切换电路结构，将电池系统转化为串联继续充电，同时改变电路限流电感值保证电池处于极限工况。仿真结果表明，普通时序串联法与优化方法都可在3s内将600mF电容器充满，但优化方案将蓄电池并联数减少1/3，极大降低了系统成本、体积与重量。搭建充电策略优化的实验平台进行实验，实验波形与仿真波形基本一致。验证了优化方案的正确性，为混合储能更好地应用于大功率电磁发射奠定了基础。

混合储能 电磁发射 充电电源 充电策略 脉冲功率技术

0 引言

新型混合储能技术能够实现脉冲电容器的快速、可靠、安全充电，是军用电磁发射中的关键技术[1-4]。与国内普遍采用的、运用于可再生能源的混合储能不同[5-12]，海军工程大学提出的新型混合储能技术将蓄电池作为脉冲电容器的充电电源[13]。蓄电池在电网与脉冲电容之间起到功率、能量缓冲作用，可有效降低大功率连续电磁发射[14]对电网的瞬时功率需求。在不使用时，以较低功率、较长时间通过电网存储能量；需要时，向电容器放电，实现高功率、可重复能量输出。蓄电池-电容器混合储能结构的特殊性[15]使其同时具备了高功率密度、高能量密度的优势。

针对这种新型储能结构，必须具备其特有的电容充电方式。由海军工程大学提出并通过实验得到验证的蓄电池时序[16]串联入网充电方式[17,18]，具有充电电流恒定、电容电压线性升高、控制简单、效率高等优势，目前最适于混合储能的能量流传递。混合储能中电池输出功率受其放电倍率限制，国内锂电池以10C～20C为极限，国际上已有放电能力是国内数倍的锂电池报道。受国内电池性能影响，只能采用多组电池并联同时输出电流的方式来满足与国外电池相同的输出能力，但会使系统过于庞大。以上不足可通过两种方式进行改进：①研发性能更好的电池；②对系统进行充电策略与结构优化。本文采用第二种方式，对时序串联策略进行改进。通过电路结构的变化，实现蓄电池先并联后串联对电容充电，在相同时间与能级要求下，降低了蓄电池并联数量，有效减少了混合储能系统的体积、重量与系统资金投入，为混合储能更好地应用于大功率连续电磁发射奠定了基础。

1 时序串联充电策略原理

1.1 原理分析

混合储能系统结构如图1所示。首先由电网以较低功率缓慢对蓄电池充电，在需要时由电池以数十MW级功率对脉冲电容充电，脉冲电容最后通过脉冲成型网络以GW功率输出到负载。因蓄电池的蓄能作用，系统可短时间内连续实现多次大功率电磁发射。

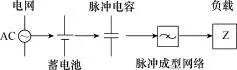
图1 混合储能系统结构Fig.1 Hybrid energy storage system structure

时序串联能量流传递原理如图2所示。图2中，蓄电池系统为En=nE0，n表示由n组电池串联入网，E0为单组电池电压。电力电子开关SC1～SC4用于控制电路导通与关断，导通开关SF1～SFn-1用于开通某一组电池放电。L为限流电感器，C为脉冲电容器，二极管VD用于续流，Rn为蓄电池系统内阻，Rn=nRe，R0为电路等效内阻。

图2 时序串联能量流传递原理Fig.2 Principle of series energy flow

时序串联充电的具体过程：首先闭合SC1、SC3、SF1，1号蓄电池组串入回路对脉冲电容器C充电，此时为第1阶段。t1时断开SF1，闭合SF2，电路进入第2阶段，蓄电池组2号与1号串联，一起对脉冲电容C充电。依次类推，直到时间tn-1，电路进入第n阶段，断开SFn-1、SC3，闭合SC4，使n号电池组串联入网，至此所有电池全部串联对电容器充电。待电容器达到所需电压时断开所有开关，充电过程结束。若将各开关动作顺序由上至下颠倒，图2电路还可实现电池触发顺序变换，从而实现各电池组均衡放电。

图3是采用图2结构实现的蓄电池对脉冲电容器时序串联充电电流波形。在tn时刻将第n组电池串联入网，使电流在一定范围内实现近似恒定，若触发时刻过早或过晚都将使电流I(t)超出此范围。只要电流接近于恒定，电容器电压就可实现近似直线上升。

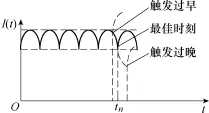
图3 时序串联充电方式电流曲线Fig.3 Current curve of orderly-serial charging mode

目前有C=600mF脉冲电容器需要在3s内充至3 200V，以现有的30A·h/3.2V（10C）锂电池进行混合储能实验，单体电池内阻为1mΩ。初步方案为两只电池并联作为最小单元，100个单元串联形成单个电池组（单组电压E0=320V），共10组对电容器充电。蓄电池系统输出最高电压为E10=3 200V，最高电流为Imax=600A。若以峰值600A对电容器充电，电容计算式为

式中，u(t)为电容电压；I(t)为充电电流；t为时间。仿真结果可知将电容器充至3 200V需要3.57s，采用两组电池并联的方式不能满足时间要求。现采用三只电池并联作为最小单元，100个单元串联形成单个电池组，仍然为10组。蓄电池系统输出最高电压仍为3 200V，输出最大电流为Imax=900A，仿真计算结果可知电池能在2.87s内将电容器充满。仿真分析蓄电池时序入网时间计算方法如下。

对照图2建立电路方程为

式中，Rn=n×33.3mΩ；R0=50mΩ；限流电感L=50mH。由各已知参数可知，满足电路为欠阻尼，求解式（2）可得

其中

式中，I(0)、u(0)为当前阶段电路初始状态。任一新阶段的初始条件为上一阶段（每串联一组电池入网为一个新阶段）最后时刻电流、电压。第一组蓄电池串联入网时，初始值已知为I1(0)=0、u1(0)=0。对式（4）求导得

只需通过式（10）求解电流峰值所对应的时间值tmax，从而求解电流峰值Imax，并使蓄电池在串联入网时电流峰值等于900A，即可计算出各电池组的入网时间节点。

1.2 仿真分析

以式（4）、式（5）和式（10）为基础，利用Matlab仿真计算采用3只电池并联为最小单元时，10个电池组的入网时间见表1。

表1 时序串联入网时间Tab.1 Connect joint time of orderly-serial

将表1时序代入Simplorer仿真得到波形如图4所示。由图4可知，采用3只并联电池作为最小单元，串联后对电容器充电，当限流电感值为50mH时蓄电池系统输出电流峰值为870A，各单体电池输出电流为290A，接近输出极限。10组电池时序串联入网，使得电流近似恒定，电容电压呈线性升高。在2.55s时电容电压达到3 203V，符合3s内指标要求。系统共使用电池数量N=3 000只。采用同样方法仿真2只电池并联的情况，得到充电时间为3.57s。

图4 时序串联充电仿真波形Fig.4 Simulation waveforms of orderly-serial charging

2 时序串联充电策略优化方案

2.1 原理分析

原方案与优化方案对比如图5所示。

图5 原方案与优化方案对比Fig.5 Comparison of the original and the optimization scheme

由图5可知，原方案采用3只电池并联为最小单元，100个单元串联后为一组，共10组时序串联入网对电容器充电，电池使用数量为3 000只。优化方案采用2只电池并联为最小单元，100个单元串联后为一组，也采用10组电池。但充电时分为两个阶段：①首先以两组并联的形式同时入网，每两组为一个大组，则10组电池分为5个大组，以大组为单位时序串联入网对电容器充电；②当5个大组全部入网后，电路电流降为0时通过电路结构变换将右侧6～10号电池组从电路中切除，将6号电池组串联到5号后端，重新采用单组串联的方式时序入网对电容器充电。优化方案阶段①相当于4只电池并联，电池系统输出最大电流可达到1 200A，从而弥补了在阶段②只能输出600A的不足。为使电路能够达到电池系统输出极限，原理由图2变换为图6。

由图6a可知，在阶段①蓄电池两组并联向电容器充电，两条支路电压为E1n=E2n=nE0（n=1～5），支路电阻R1n=R2n=50n(mΩ)。限流电感L3=100mH，支路限流电感L1=50mH、L2=50mH。开关SF闭合，将限流电感L3从电路中移除。由于此电路为时不变线性电路，可通过等效原理建立电路方程，即

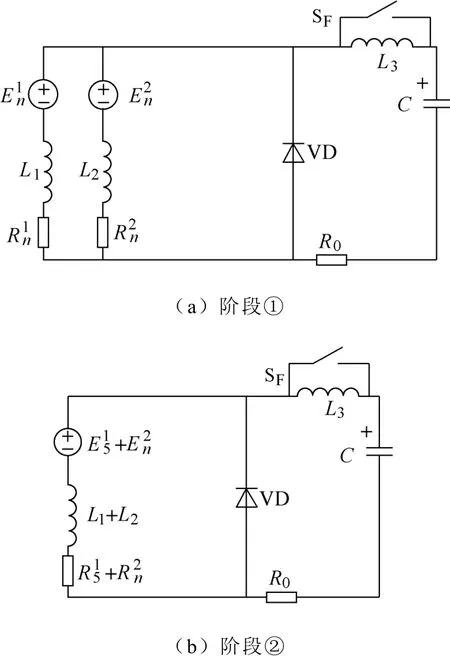
图6 改进方案原理示意图Fig.6 Principle of amelioration scheme

此阶段电路参数同样满足

采用与前述相同方法求解电路，得到此情况下电容器充电电流I(t)、电压u(t)与电流峰值Imax，并通过Matlab仿真计算阶段①各电池入网时序，见表2。

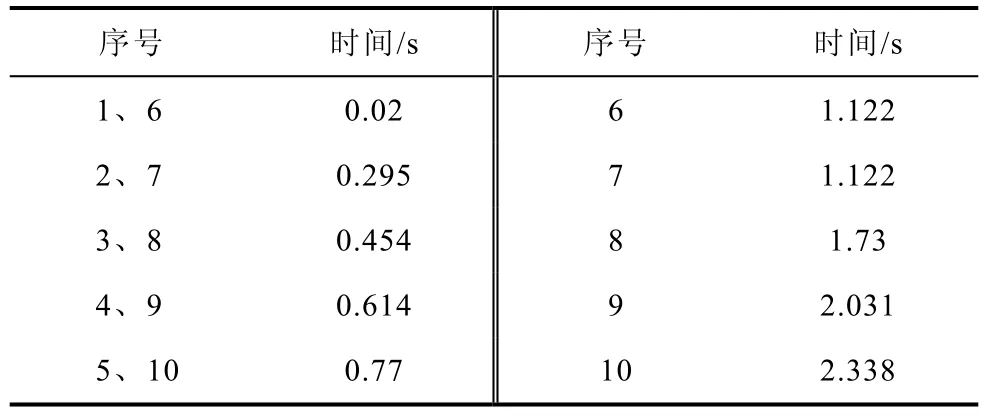
表2 优化方案入网时间Tab.2 Connect joint time of amelioration scheme

观察图6b，进入阶段②后，将两条支路电池转换为串联，断开开关SF使电感器L3重新接入电路。因此时1～5号电池已经入网，将6～10号电池按时序接入，电源电压E15+E2n=320V×5+E2n。电源等效电阻为R15+R2n=50mΩ×5+R2n。阶段切换时，对电感器作如上调整的目的在于保证无论电路结构如何切换，蓄电池输出电流始终处于极限。同样，进行电路求解与Matlab仿真得到阶段②后5组电池入网时间，见表2。

图6为改进方案原理示意图，主要为描述方便，若要完成图6中所示的结构切换，需采用图7所示优化策略电路结构。

图7 优化策略电路结构Fig.7 The circuit configuration of amelioration scheme

图7中只需闭合SC10、SC12，断开SC11、SC9即为图6a，断开SC10、SC12，闭合SC11、SC9即为图6b。

2.2 仿真分析

按照表2时序用Simplorer进行仿真得到波形如图8所示。表2中6、7号电池组触发时序相同即同时触发，其主要原因在于触发单组电池时电流峰值远小于600A，电池并未处于极限输出工况，这将延长充电时间，降低系统输出功率。所以，此时选择两组电池同时触发来增加电池系统输出电流。图8a中，充电电流进入阶段②时，后5组电池充电，但电流只存在4个波峰。

图8 优化方案仿真波形Fig.8 Simulation waveforms of amelioration scheme

观察图8，在阶段①蓄电池系统输出电流峰值为1 187A，各单体电池输出峰值为296A。阶段②电池系统输出电流峰值为596A，各单体电池输出电流峰值为298A。电池都处于极限放电状态。电容器电压在2.87s时达到3 201V，满足3s内指标。可见，在相同的时间内要求将电容器充满，优化方案使用电池数量N=2 000只，比原方案蓄电池数量减少了1/3。综上分析，通过对电路结构切换与控制策略的优化，可弥补电池放电能力的不足。

2.3 一般性分析

本节将在以上具体实例描述基础上进行一般性描述，进一步说明此优化策略的优势。设电池组并联数为m，单体电池的最大输出电流为I0。因串联时序充电方法实现了电容器的近似恒流充电，由式（1）可知电容器的充电速率为

是夜，就在我多次痛快淋漓地排泄之后，依旧不能熟睡。不过，我的状态好多了，虽说不能熟睡，毕竟是能睡了。尽管仅睡了一个多小时便被咳嗽震醒了。老婆嫌我吵，便睡眼朦胧地抱着枕头跑去小屋了。也幸亏她去了小屋，不然，这一夜她又要失眠了。我咳罢又睡，睡罢再咳醒，一夜竟然如此折腾了四、五回。

此时，将电容器充到所需电压的时间为

若采用优化策略充电，则前0.5u(t)充电电流为2I0m，后0.5u(t)充电电流为I0m。此时电容器的充电时间为

可见，采用优化策略后电容器充电效率提高了25%。在以上实例中，两只电池并联，达到所需电压仿真时间为3.57s，而采用优化策略后的时间为2.87s，系统效率提高20%，没有达到25%的原因是电流在整个过程中并非真正恒流，只是近似。综上所述，本优化策略并不仅限于以上工程实例，其在任何工况下都可在不增加电池数量的情况下大大提高充电效率。

从另一角度出发，在相同时间要求下，优化方案可降低电池并联数。当并联数为m的充电速度小于并联数为m-x的速度的1.25倍时(Vm-x＜Vm＜1.25Vm-x)，采用优化方案后并联数可从m缩减到m-x且不影响充电效率。x取值不限于本文实例描述中的1，必须以实际工况决定。由于电磁发射混合储能主要应用于短时脉冲工况，以目前国内的大倍率（10C～20C）功率型电池单体释放几百/上千安培而言，当m＞5时电流可以达到几千安培，这已超出了很多的实际使用工况。所以蓄电池的并联数不能太高，即使x取值为1时，带来的效益也是相当可观的。

3 实验

搭建混合储能优化方案验证平台。实验电路与图7相同，各器件参数与仿真参数一致。实验与仿真波形对比如图9所示。

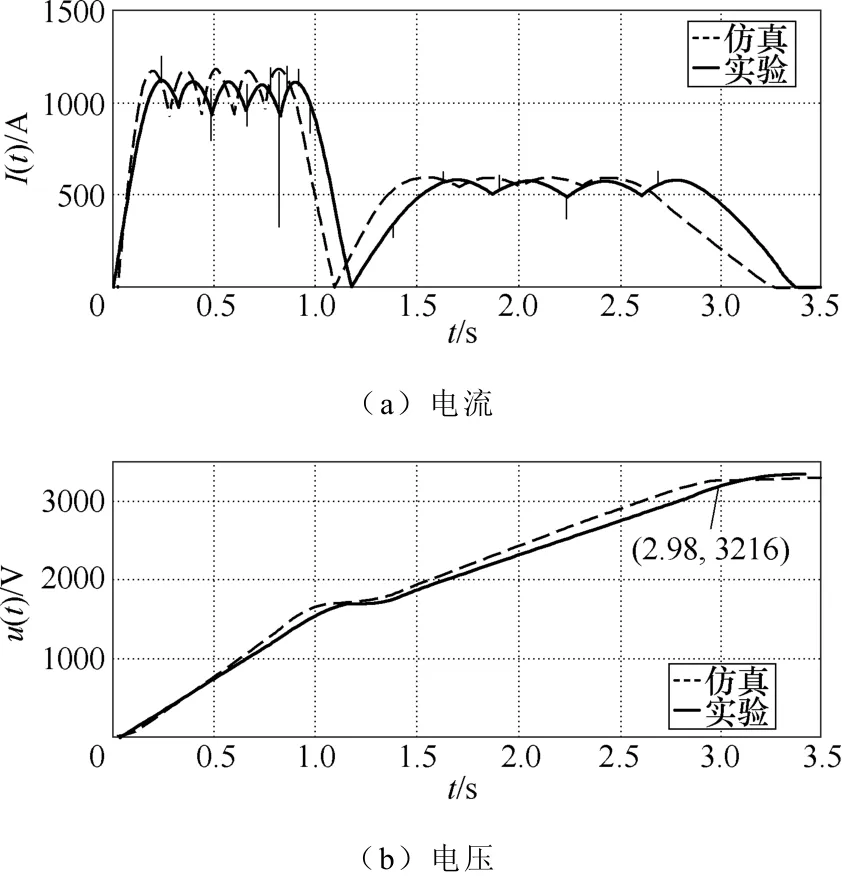
图9 实验与仿真波形对比Fig.9 Comparison of experiment and simulation waveforms

由图9可知，仿真波形与实验波形基本一致，细微差别是由电路等效参数选取误差产生的。实验电压曲线在2.98s达到3 216V，满足指标要求。图10为实验平台电池组、电容实物。

图10 实验平台Fig.10 Experiment platform

4 结论

[1] Pokryvailo A, Wolf M, Yankelevich Y. Investigation of operational regimes of a high-power pulsed corona source with an all solid state pulser[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2006, 14(4)： 846-857.

[2] Akiyama H, Sakugawa T, Namihira T. Industrial applications of pulsed power technology[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2007, 14(5)： 1051-1064.

[3] Mark C, Ravi S, Trevor W. The design and testing of a large-caliber railgun[J]. IEEE Transactions on Magnetics, 2009, 45(1)： 256-260.

[4] 李军, 严萍, 袁伟群. 电磁轨道炮发射技术的发展与现状[J]. 高电压技术, 2014, 40(4)： 1052-1064. Li Jun, Yan Ping, Yuan Weiqun. Electromagnetic gun technology and its development[J]. High Voltage Engineering, 2014, 40(4)： 1052-1064.

[5] 丁明, 林根德, 陈自年, 等. 一种适用于混合储能系统的控制策略[J]. 中国电机工程学报, 2012, 32(7)： 1-6. Ding Ming, Lin Gende, Chen Zinian, et al. A control strategy for hybrid energy storage systems[J]. Proceedings of the CSEE, 2012, 32(7)： 1-6.

[6] Thounthong P, Rael S, Davat B. Control strategy of fuel cell and super capacitors association for a distributed generation system[J]. IEEE Transactions on Industrial Electronics, 2007, 54(6)： 3225-3233.

[7] 徐剑鸣, 康龙云, 温懋勤, 等. 电动汽车复合能源系统设计[J]. 电力系统自动化, 2012, 36(3)： 60-66. Xu Jianming, Kang Longyun, Wen Maoqin, et al. Design of hybrid power system of electric vehicle[J].Automation of Electric Power Systems, 2012, 36(3)：60-66.

[8] Nishad M, Kashem M, Sarath P. Management of battery-supercapacitor hybrid energy storage and synchronous condenser for isolated operation of PMSG based variable-speed wind turbine generating systems[J]. IEEE Transactions on Smart Grid, 2014, 5(2)： 944-954.

[9] 郑文迪, 蔡金锭. 燃料电池/超级电容器混合发电系统能量管理策略[J]. 电力自动化设备, 2012, 32(12)： 28-32. Zheng Wendi, Cai Jinding. Energy management strategy for hybrid generation system with fuel cell and super-capacitor[J]. Electric Power Automation Equipment, 2012, 32(12)： 28-32.

[10] 张纯江, 董杰, 刘君, 等. 蓄电池与超级电容混合储能系统的控制策略[J]. 电工技术学报, 2014, 29(4)： 334-340. Zhang Chunjiang, Dong Jie, Liu Jun, et al. A control strategy for battery-ultracapacitor hybrid energy storage system[J]. Transactions of China Electrotechnical Society, 2014, 29(4)： 334-340.

[11] 韩晓娟, 程成, 籍天明, 等. 计及电池使用寿命的混合储能系统容量优化模型[J]. 中国电机工程学报, 2013, 33(34)： 91-98. Han Xiaojuan, Cheng Cheng, Ji Tianming, et al. Capacity optimal modeling of hybrid energy storage systems considering battery life[J]. Proceedings of the CSEE, 2013, 33(34)： 91-98.

[12] 常丰祺, 郑泽东, 李永东. 一种新型混合储能拓扑及其功率分流算法[J]. 电工技术学报, 2015, 30(12)：128-136. Chang Fengqi, Zheng Zedong, Li Yongdong. A novel hybrid energy storage topology and its power sharing algorithm[J]. Transactions of China Electrotechnical Society, 2015, 30(12)： 128-136.

[13] 高迎慧, 史孝侠, 严萍. 高功率密度电容器充电电源[J]. 强激光与粒子束, 2012, 24(4)： 943-949. Gao Yinghui, Shi Xiaoxia, Yan Ping. High power density capacitor charging power supply[J]. High Power Laser and Particle Beams, 2012, 24(4)： 943-949.

[14] 龚晨, 于歆杰, 刘秀成. 电容储能型轨道炮连续发射系统设计与仿真[J].电工技术学报, 2013, 28(2)：111-115. Gong Chen, Yu Xinjie, Liu Xiucheng. Continuous emission scheme and its simulation for capacitor based railgun system[J]. Transactions of China Electrotechnical Society, 2013, 28(2)： 111-115.

[15] 吴海峰. 大功率混合储能装置控制策略研究[J]. 西安交通大学学报, 2015, 101(2)： 93-98. Wu Haifeng. Study of discharge control strategy for high power lead-acid batteries[J]. Academic Journal of Xi’an Jiaotong University, 2015, 101(2)： 93-98.

[16] 范昭楠, 于歆杰. 基于过程集成的电磁轨道炮脉冲电源多目标优化[J]. 电工技术学报, 2010, 25(5)：20-24. Fan Zhaonan, Yu Xinjie. Process-integration based multi-objective optimization for pulsed power supply of electromagnetic guns[J]. Transactions of China Electrotechnical Society, 2010, 25(5)： 20-24.

[17] 李超, 鲁军勇, 江汉红, 等. 电磁发射用多级混合储能充电方式对比[J]. 强激光与粒子束, 2015, 27(7)： 075005(1-6). Li Chao, Lu Junyong, Jiang Hanhong, et al. Comparison of charging methods of multilevel hybrid energy storage for electromagnetic launch[J]. High Power Laser and Particle Beams, 2015, 27(7)：075005(1-6).

[18] 李超, 鲁军勇, 江汉红, 等. 混合储能中电容器电压精确控制策略研究[J]. 高电压技术, 2015, 41(7)：2231-2235. Li Chao, Lu Junyong, Jiang Hanhong, et al. Study of capacitor voltage’s precise-control strategy of multilevel hybrid energy storage[J]. High Voltage Engineering, 2015, 41(7)： 2231-2235.

（编辑 张洪霞）

Charging Strategy Amelioration of Multilevel Hybrid Energy Storage for Electromagnetic Launch

Li Chao Lu Junyong Ma Weiming Jiang Hanhong Long Xinlin
（National Key Laboratory of Science and Technology on Vessel Integrated Power System Navy University of Engineering Wuhan 430033 China）

Strategy of series-on-schedule uses parallel-connected batteries to meet high power requirement. It makes the system too big and heavy. This article constituted the improving scheme based on series-on-schedule strategy. Firstly, it paralleled the batteries to charge the capacitor. Secondly, it changed the configuration of batteries from parallel to series. At the same time, the inductance should be regulated to insure the batteries were in the utmost work status. The simulation results show both the series-on-schedule and the new scheme can charge the 600mF capacitor to requisite voltage in 3s, but the new scheme can cut down the number of batteries by 1/3. It reduces the spending, volume and the weight of the system largely. The experimental results show the simulation curves can match the real situation well. At last the conclusion can be drawn that the new scheme is validate and realizable.

Hybrid energy storage, electromagnetic launch, charging power supply, charging strategy, pulse power technology

TM832

李 超 男，1988年生，博士研究生，研究方向为电磁发射。

E-mail： lichao69@126.com（通信作者）

鲁军勇 男，1978年生，教授，博士生导师，研究方向为电磁发射。E-mail： jylu@xinhuanet.com

10.19595/j.cnki.1000-6753.tces.151727

国家自然科学基金（51522706、51407191、51307176），实验室基金（9140C840409140C84026、9140C840409150C84358）和国家重点基础研究发展计划（973计划）（613262）资助。

2015-10-23 改稿日期 2016-03-25