关于连续映射半群拓扑熵的一点注记

田延国,马东魁

(华南理工大学数学学院,广东广州 510641)

关于连续映射半群拓扑熵的一点注记

田延国,马东魁

(华南理工大学数学学院,广东广州 510641)

本文研究了度量空间中连续映射构成半群的拓扑熵.利用Patro[8]的方法,给出了度量空间中两种有限个连续映射构成的半群的拓扑d-熵的定义,比较了两种拓扑d-熵的大小.证明了局部紧致可分度量空间上有限个真映射构成的半群的拓扑d-熵和它的一点紧化空间上对应的拓扑熵相等.上面结果推广了Patro的相应结论.

拓扑熵;半群;真映射;度量空间

1 引言

拓扑熵是动力系统中一个非常重要的量,可用来刻画系统的复杂度.从Adler,Konheim和McAndrew[1]首先给出拓扑熵的定义以来,拓扑熵的研究逐渐发展成为动力系统的一个重要方向.随着研究的深入及新问题的出现,人们从各个角度研究和推广拓扑熵,如文献[4,6,12].其中一个重要方向就是半群作用系统的拓扑熵.首先,Bi[2]和Bufetov[5]分别给出了紧致度量空间上有限个连续映射构成的半群的拓扑熵的定义.在此基础上,人们又深入研究了这两种拓扑熵,比如针对紧致度量空间上有限个连续映射构成的半群系统,Ma和Wu[7]定义了任意子集的拓扑熵;Wang和Ma[10]及Wang,Ma和Lin[9]分别推广Bi[2]和Bufetov[5]的拓扑熵,给出了一般度量空间上由有限个一致连续映射构成的半群的拓扑熵的定义.

在此基础上,我们将Bufetov[5]紧致度量空间中有限个连续映射构成半群的拓扑熵的定义推广到一般的度量空间中,定义了一种度量空间中有限个连续映射构成半群的拓扑d-熵.然后将Bi[2]在紧致度量空间中拓扑熵的定义推广到一般的度量空间中,定义另一种度量空间中有限个连续映射构成半群的拓扑d-熵,比较了两种定义的拓扑d-熵的大小,并且证明局部紧致可分度量空间上有限个真映射构成的半群的拓扑d-熵和它的一点紧化空间上对应的拓扑熵相等.

2 预备知识

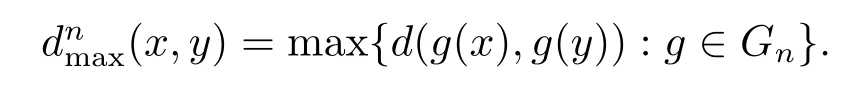
对任意的ε＞0,n∈N,X的子集E称为X的(n,ε)张成集,若对每一个x∈X,存在y∈E满足d(g(x),g(y))≤ε,其中g∈Gn.记X的所有(n,ε)张成集的最小基数为r(n,ε,X,G1).Bi´s定义了由G1生成的半群G的拓扑熵

下面介绍Bufetov[5]的定义.设X为紧致度量空间,X上的度量记为d,fi：X→X为连续映射 (i=0,1,···,m-1),记,用G′表示由生成的半群.记={w|w=w0w1···wk,wi=0,1,···,m-1}. 若存在满足w=w′′w′,记为w′ ≤w. 对w∈,w=w1w2···wk,记 |w|=k,fw=fw1fw2···fwk,则显然fww′=fwfw′.对每一个w∈,X上的度量定义为

Bufetov[5]定义了半群的拓扑熵

我们可用Bufetov方法定义了拓扑d-熵.设X为一个度量空间,fi：X→X为连续映射(i=0,1,···,m-1).令Y为X的子集,对任意的w∈,ε＞0,F⊂X称为Y的(w,ε,)张成集,若对任意的x∈Y,存在y∈F满足dw(x,y)≤ε.记Y的所有(w,ε,)的最小基数为B(w,ε,Y,).

定义2.1设(X,d)为一个度量空间={f0,f1,···,fm-1},其中fi：X→X为连续映射(i=0,1,···,m-1).Y为X的子集,定义,其中

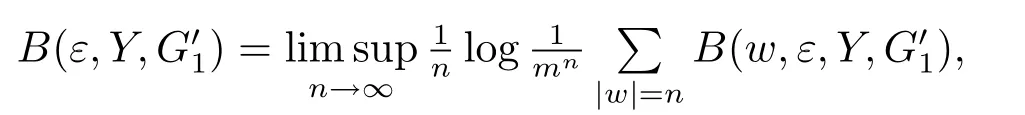
则可定义X关于生成半群的拓扑d-熵为,其中上确界取遍X的所有子集Y.

注2.1(1)当X为紧致度量空间时,定义2.1与Bufetov的定义等价,即

(2)当X为度量空间,fi均为一致连续时,定义2.1与文献[9]中定义等价.

下面给出真映射[8]的概念.设X为一个拓扑空间,T：X→X为连续映射,称T为真映射,若X的任意紧致子集在T下的原像为紧致子集.

3 本文定义的拓扑d-熵及主要结果

令Y为X的子集,对任意的ε＞0,n∈N,E⊂X称为Y的(n,ε)张成集,若对任意的x∈Y,存在y∈E满足.记Y的所有(n,ε)张成集的最小基数为r(n,ε,Y,G1).

定义3.1设(X,d)为一个度量空间,G是由集合G1={idX,f0,f1,···,fm-1}生成的半群,其中fi：X→X为连续映射(i=0,1,···,m-1).Y为X的子集,定义

其中

可定义由G1生成的半群G的拓扑d-熵为,其中上确界取遍X的所有子集Y.

注3.1(1)当X为紧致度量空间时,定义3.1与Bi[2]的定义等价,即hd(G1)=h(G1).

(2)当X为度量空间,fi均为一致连续时,定义3.1与文献[10]中定义等价.

(3)hd(G1)=hd(G1,X).

下面可以比较定义2.1和定义3.1中两种度量空间中有限个连续映射构成的半群的拓扑d-熵的大小.

定理3.1设(X,d)为一个度量空间,G1={idX,f0,f1,···,fm-1},G′1={f0,f1,···,fm-1},其中fi：X→X为连续映射(i=0,1,···,m-1).则

证对X的任意子集Y以及n∈N,对任意的ε＞0,若M为Y的(n,ε,G1)张成集,则对任意的x∈Y,存在y∈M满足ε.由上式可推出d(fw(x),fw(y))≤ε,其中.即Y的(n,ε,G1)张成集为Y的(w,ε,)张成集,从而有

进而

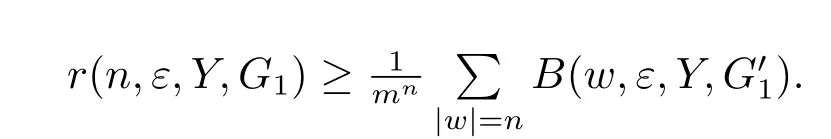
两边同时取log,除以n及取极限可得,由Y的任意性,两边对Y取上确界,可得,证毕.

令X为局部紧致可分度量空间,它的一点紧化空间记作.fi：X→X(i=0,1,···,m-1)为真映射.定义且

下面的定理说明了局部紧致可分度量空间上有限个真映射构成的半群的拓扑d-熵和它的一点紧化空间上对应的拓扑熵相等.

定理3.2设X为一个局部紧致可分空间,为X的一点紧化空间.度量d是上的度量在X上的限制.G是由集合G1={idX,f0,f1,···,fm-1}生成的半群,其中fi：X→X为真映射(i=0,1,···,m-1),1={idX,0,···,m-1}.则有,其中h(1)表示Bi´s定义的由1生成的半群的拓扑熵.

证首先说明对任意的n∈N及ε＞0,有r(n,ε,G1)是有限的.令的一个张成集.由X在中的稠密性,存在{x1,···,xk}⊂X满足.对任意的x∈X⊂,存在满足.由上可得

故

S

={

x

1

,···,xk

}为

X

的(

n,ε,G

1

)张成集.若选取

的元素个数为

,则可得

反之,令U={x1,···,xk}为X的张成集.对任意的,由X在中稠密,则存在x∈X满足,从而有xi∈U满足.于是

故U={x1,···,xk}为的(n,ε,1)张成集.若选取U的元素个数为r(n,ε,G1),可得

结合(3.2)和(3.3)式可得

[1]Adler R L,Konheim A G,McAndrew M H.Topological entropy[J].Trans.Amer.Math.Soc.,1965,114(2)：309-319.

[4]Bowen R.Entropy for group endomorphisms and homogeneous spaces[J].Trans.Amer.Math.Soc.,1971,153(1)：401-414.

[5]Bufetov A.Topological entropy of free semigroup actions and skew-product transformations[J].J.Dynam.Control Sys.,1998,5(1)：137-143.

[6]Dinaburg E I.The relation between topological entropy and metric entropy[J].Soviet Math.Dokl,1970,11(1),13-16.

[7]Ma Dongkui,Wu Min.Topological pressure and topological entropy of a semigroup of maps[J].Discrete Contin.Dyn.Sys.,2011,31(2)：545-557.

[9]Wang Yupan,Ma Dongkui,Lin Xiaogang.On the topological entropy of free semigroup actions[J].J.Math.Anal.Appl.,2006,435(2)：1573-1590.

[10]Wang Yupan,Ma Dongkui.On the topological entropy of a semigroup of continuous maps[J].J.Math.Anal.Appl,2005,427(2)：1084-1100.

[11]Waters P.An introduction to ergodic theory[M].New York,Heidelberg,Berlin：Springer-Verlag,1982.

[12]彭丽.低复杂度序列的维数[J].数学杂志,2006,26(2)：133-136.

A REMARK ON THE TOPOLOGICAL ENTROPY OF A SEMIGROUP OF CONTINUOUS MAPS

TIAN Yan-guo,MA Dong-kui
(School of Mathematics,South China University of Technology,Guangzhou,510641,China)

In this paper,we study the topological entropy of a semigroup of continuous maps on a metric space.By using Patro’s[8]method,we give two de fi nitions of topologicald-entropy of a semigroup generated by fi nite continuous maps on a metric space,the size of these twod-entropies are compared.We also show that the topologicald-entropy of the semigroup generated by fi nite proper maps on a locally compact separable metric space and the topological entropy on its one-point compacti fi cation space coincide,which extend the results obtained by Patro.

topological entropy;semigroup;proper maps;metric space

on：37A35;37B40

O189.1

A

0255-7797(2017)04-0792-05

2016-08-03接收日期：2016-10-31

国家自然科学基金资助(11671149);广东省自然科学基金资助(2014A030313230);中央高校基础研究基金资助(SCUT(2015ZZ055;2015ZZ127)).

田延国(1990-),男,山东德州,硕士,主要研究方向：拓扑动力系统与遍历理论.