竞争环境下基于顾客离散选择的酒店房间动态定价研究

许雪琦，陈 思，李真真

（杭州电子科技大学 管理学院，浙江 杭州 310018）

竞争环境下基于顾客离散选择的酒店房间动态定价研究

许雪琦，陈 思，李真真

（杭州电子科技大学 管理学院，浙江 杭州 310018）

针对竞争环境下两酒店的动态定价策略问题，首先运用M N L模型来描述顾客在多房间多价位间的选择行为，通过假设实时房间余量是已知信息，得到纳什均衡，并构建了完全信息下的动态定价模型；在此基础上，提出一种启发式插值策略，建立非完全信息下的动态定价模型。最后通过仿真分析表明，非完全信息下启发式插值策略能有效的提升酒店的效益。

动态定价；M N L模型；启发式插值算法；纳什均衡

一、引言

近年来随着互联网和移动终端迅速发展，房间预订系统也逐步完善，使得酒店动态定价也越来越重要。动态定价是为了获得最大收益而实时调整库存的一种策略，它适用于库存固定且未售出的产品价值残值为零的产品或服务。现在已经在酒店[1]、汽车出租、飞机客运、公路运输、旅游[2]等行业得到广泛运用。

传统的动态定价主要集中在垄断模型，如Dudey等[3]研究了两个出售替代品的双寡头垄断模型。随着技术的发展和产品市场的逐步发展，顾客需求产生多样变化，因此在动态定价过程中竞争因素越来越重要，学者对于研究供应链中供应商的竞争关系的兴趣逐渐增加。罗利等[4]引入竞争因素，将动态定价运用到飞机客运中；李豪等[5]从顾客策略出发，研究了竞争环境下两零售商的动态定价策略。朱志愚等[6]考虑顾客离散选择行为，建立了竞争环境下两家航空公司三级价格等级的动态定价模型。Talluri和Van Ryzin[7]研究了单房间类型存在需求相关性时的酒店动态定价问题。陈武华等[8]研究了基于顾客选择的酒店多房间类型联合定价。

综合国内外研究成果看，针对酒店动态定价问题，发现仍存在一些不足：（1）竞争环境是动态定价考虑的重要因素，已有的研究中并没有考虑竞争因素；（2）有些易逝品动态定价考虑竞争因素的引入，但仅在能获取竞争对手实时库存的情况下进行产品或服务的定价，没有考虑到缺乏实时库存信息时如何定价。本文将针对上述两点展开，对竞争环境下酒店不能获取竞争对手实时库存情况下的价格策略进行深入研究。

二、问题描述

假设市场上存在两家竞争酒店，在预定期[0，T]将房间预订出去，酒店在仅能获取竞争酒店初始房间余量而不能获取酒店实时余量的情况下制定价格pi，以获取利益最大化。

符号说明：c1和c2分别代表酒店1和2的初始房间余量，s1和s2代表实时房间余量，αi代表酒店的质量、品牌效应和受欢迎程度，β代表价格反应参数。

三、数学模型的建立与求解

（一）顾客选择模型[9]（MNL模型）

MNL模型是一个随机效用最大化模型，能根据顾客效用最大化进行选择，被广泛应用于描述消费者的购买行为。

假设顾客到达服从伯努利过程，每个阶段有顾客到达的概率为λ，保证每个阶段都有顾客到达。在每个时间段，顾客会比较所有酒店的价格然后决定是否预订房间。本文用MNL模型来确定顾客的离散选择，对于每个顾客来说，从酒店i购买房间的概率：

（二）完全信息

假设两个酒店都知道对方的实时客房余量，即掌握完全信息，这种情况下存在纳什均衡。首先考虑单周期，当 T=1，假设库存 ci≥1，酒店 i的收入函数是：

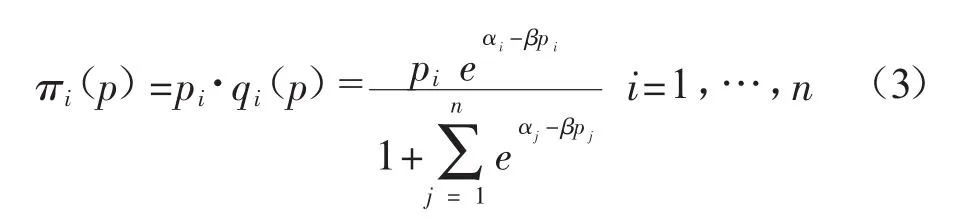
如果在时间段t没有顾客到达，那么酒店保留房间到时间段t-1。如果有顾客在t阶段到达，那么酒店间的博弈是选择价格pi最大化收益函数：

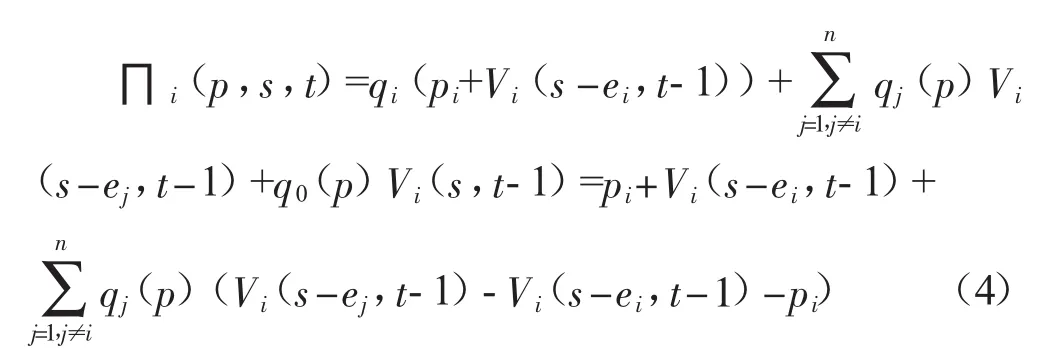
ei：1*n 的单位矩阵

S：现有客房集合

Vi（s，t-1）：酒店i在t-1到1阶段所有酒店使用纳什均衡的情况下的期望收益

如果存在纳什均衡 p*（s，t），那么从时间段 t到时间段1，i酒店的纳什均衡期望收益是：

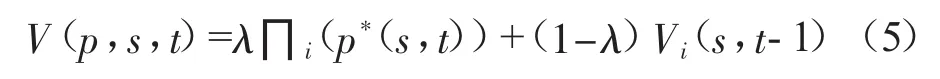
（三）不完全信息

假设两个酒店均不知道对方的实时客房余量，如果客房余量大于可能到达的顾客数量，在这种情况下，纳什均衡里每个酒店都有固定的价格，酒店没必要实行动态定价，短视价格就是纳什均衡价格。顾客越多或酒店客房余量越少动态价格的影响就会越显著。

由此，本文提出一种插入纳什均衡价格的启发式策略。这一策略假设其他酒店匀速预订出房间，自身的价格是纳什均衡价格。根据规律，完全竞争模型的插入价格应该和纳什均衡价格相近。

下面的算例以酒店1的角度详细阐述启发式策略。

（1）时间段是T，酒店i的初始客房余量是ci，i=1，2，令价格等于平衡价格 p*（c1，c1，T）

（2）在时间段 t，t=T-1，T-2，…，1，观察现有的客房余量s1，比较a2=c2t/T和d2=|a2|

（3）价格受 s1，c2，t和 T 的影响，等于

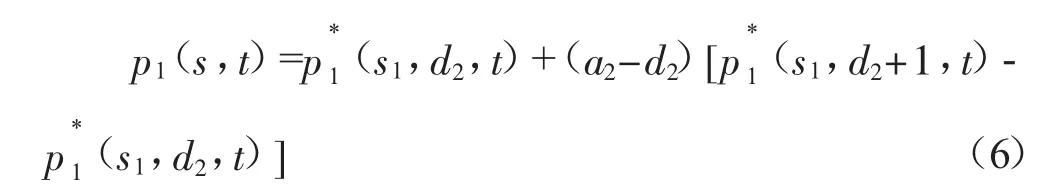
此策略线性插入了纳什均衡价格，把这个策略叫启发式插值策略。这个插入策略可以由公式（6）的两个酒店很容易扩展到2n-1个酒店：

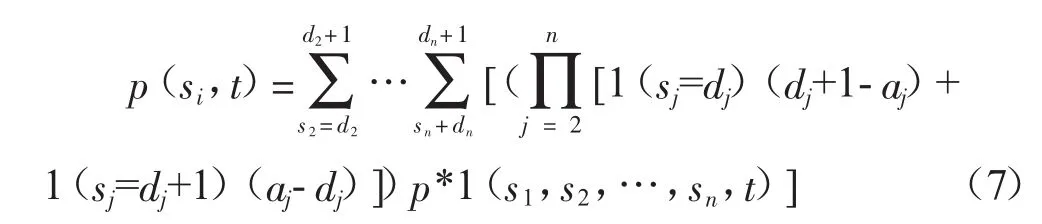
其中 ci是酒店 i的初始库存水平，ai=cit/T，di=|ai|，i=2，…，n，对于函数 l（A），如果 A 为真，l（A）=1；如果A为假，l（A）=0。

四、模型仿真与分析

为了证明插值策略的有效性，基于酒店1的角度，分别将三种策略与均衡策略a进行比较。

（1）策略b：酒店2在完全知道酒店1的信息情况下最大化自身收益。

（2）策略c：两个酒店都没有掌握对方的完全信息，均使用插值算法。

（3）策略 d：酒店 2掌握完全信息，最小化酒店1的收益，就是通常说的掠夺价格，这种期望收益提供一个较低的界限。

参数设置如下：c1=30，a1=1，a2=2，β＝0.01，T＝2000，λ=0.1。得到三种策略下两酒店的收益表（见表1）。

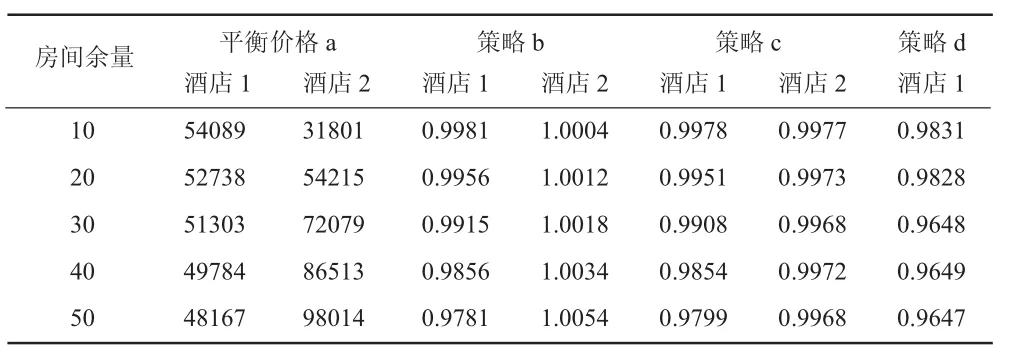
表1 均衡策略与策略b、c、d的期望收益表

为了便于说明，本文利用MATLAB根据表1中的数据绘制了两酒店在四种策略下的期望收益趋势图（见图1）：

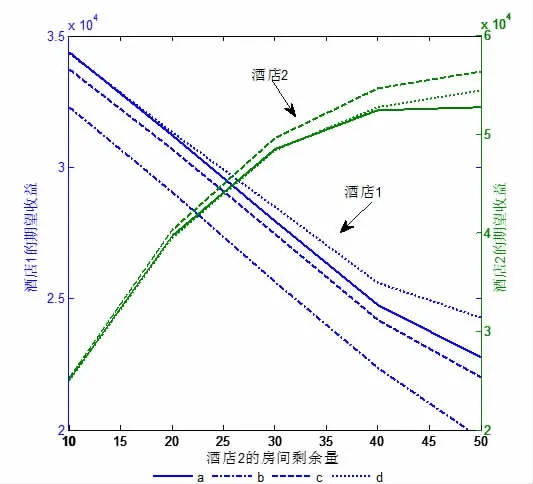
图1 两酒店期望收益趋势

结合图表，可以看出策略b中酒店2在掌握完全信息时选择的最优价格与均衡价格接近，酒店1本身是插值价格，故两酒店的价格均接近于均衡价格。从表中数据的接近程度和图中线基本重合，可证明插值策略的有效性。

策略c中，酒店1即使不能获取完全信息，但使用插值算法仍然保持了均衡收益99%以上，收益基本不受非完全信息的影响。酒店2也是如此，在非完全信息的情况下，以插值策略实现了收益基本无损失。由此可见，即使酒店不能获取竞争对手的实时房间余量，也可以通过实行插值策略保证较好的收益，证明了插值算法的有效性。

策略d中，插值算法有一个很低的边界。在这些算例里面，低的边界值保证酒店2实行掠夺价格的情况下酒店1还能保证期望收益是纳什均衡的95%以上。为了最小化酒店1的收益，酒店2降低价格吸引顾客，从而减少酒店1房间预订量。随着房间余量的增加，更多顾客选择在酒店2预订房间，即使酒店1使用均衡价格顾客依旧很少。换言之，产生均衡收益差别和低边界的主要原因是酒店2的最低价格决定的，而不是均衡价格与插值价格的区别造成的。

五、结论与展望

通过对仿真结果分析，在竞争市场上，考虑顾客离散选择行为的动态定价策略中，即使酒店不能获取完全信息，也可通过采取插值策略来减少、甚至免去酒店搜寻竞争对手实时信息的时间和金钱成本，从而提高酒店的效率与收益，这种方法值得酒店管理者借鉴。

在未来的研究中，应该注意两个问题。首先，因为很多顾客不只需要一间房间，因此批量需求处理是很有必要的。另外，如果一个酒店愿意付出代价获取每个竞争者的实时房间余量，那么哪个酒店的实时房间余量最容易获取、花费多少成本获取、在什么时间获取将成为研究的重点。这些问题的研究将帮助一个酒店在竞争市场中有效提升收益管理的效益。

[1]陈武华，孙燕红，华中生，2013.基于顾客选择的酒店多房间类型联合定价研究[J].管理科学学报（7）：23-33.

[2]尤阳，罗利，罗太波，2013.基于收益管理的旅游景点动态定价和票源控制研究[J].软科学（1）：137-140.

[3]Dudey M.Dynamic Edgeworth-Betrand competition[J].The Quarterly Journal of Economics，1992，4（107）：1461-1477.

[4]罗利，彭际华，2007.竞争环境下的民航客运收益管理动态定价模型[J].系统工程理论与实践（11）：15-25.

[5]李豪，熊中楷，彭志强，2011.竞争环境下基于顾客策略行为的易逝品动态定价研究[J].中国管理科学（2）：88-98.

[6]朱志愚，王宗宝，刘燕，2016.竞争环境下多价格等级的平行航班动态定价模型研究[J].科技和产业（9）：106-112.

[7]K A，Van Ryzin G.Revenue management under a general discrete choice model of consumer behavior[J].Management Science，2004，1（50）：15-33.

[8]陈武华，孙燕红，华中生，2013.基于顾客选择的酒店多房间类型联合定价研究[J].管理科学学报（7）：23-33.

[9]Kress D，Pesch E.Competitive Location and Pricing on Networks with Random Utilities[J].2016，16（3）：837-863.

（责任编辑：D 校对：T）

F719.2

A

1004-2768（2017）05-0100-03

2017-02-02

青年科学基金项目（71602045）

许雪琦（1974-），女，河北秦皇岛人，博士，杭州电子科技大学管理学院副教授，研究方向：管理科学、物流管理；陈思（1993-），女，湖北天门人，杭州电子科技大学管理学院硕士研究生，研究方向：数据分析、服务管理；李真真（1991-），女，河南开封人，杭州电子科技大学管理学院硕士研究生，研究方向：服务管理。