一种GNSS高精度动态解算中改进的LAMBDA算法及应用

孟宪伟，斯庭勇

（安徽四创电子股份有限公司，合肥 230031）

一种GNSS高精度动态解算中改进的LAMBDA算法及应用

孟宪伟，斯庭勇

（安徽四创电子股份有限公司，合肥 230031）

1 引言

单历元高精度的基线解算依赖于正确的模糊度值，模糊度固定是单历元动态基线解算的核心。获得厘米级的测量精度，就必须对载波相位的整周模糊度进行精确解算[1]。改进的LAMBDA算法在常规LAMBDA算法基础上进一步去相关和缩小模糊度搜索空间，从而提高了模糊度解算效率，为工程应用提供理论基础。

利用改进的LAMBDA模糊度搜索算法进行单历元定位的最大优势是快速实时性，能够及时发现大的位移形变情况，在位移较大时，是常规静态测量无法取代的。利用载波相位建立解算变形信息的数学模型，搭建形变监测平台，获取建筑物、桥梁、滑坡等形变大数据，对于掌握这些载体形变趋势，预判形变时间，为相关政府部门提供决策依据具有重要作用。

2 改进的Lambda算法介绍

2.1 LAMBDA算法

LAMBDA算法是由1993年荷兰Delft大学的Teunissen教授提出的最小二乘模糊度降相关平差法。该方法可缩小整周模糊度搜索范围，加快搜索过程，是目前快速定位中较成功的一种模糊度搜索方法[2]。由最小二乘原理求得双差模糊度的浮点解及其方差协方差阵分别为：

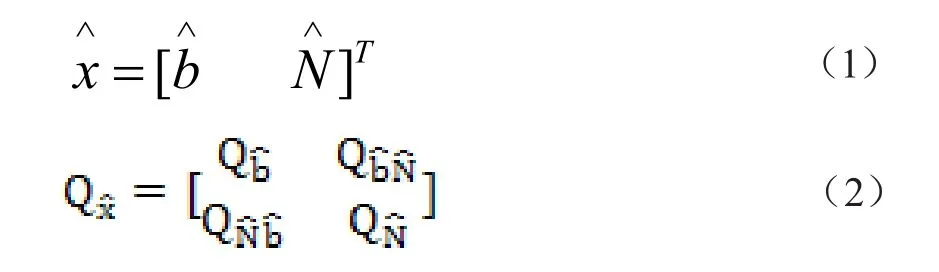
式中，QN∧反映了的精度，当精度足够高时，用LAMBDA算法搜索到的最佳候选点即为模糊度的正确解[3]。LAMBDA算法固定整周模糊度的主要过程如下：

2.1.1 整数变换

2.1.2 模糊度搜索

式中，z∈Zn，由于上式无法直接求解，故采用搜索算法从备选组中将满足上式的整数组合z挑选出来[5]。由于变换后的新参数的方差及参数间的互相关性均较前大大减小，搜索工作更为简便、迅速。由上述搜索过程求得的最优整数组合 进行逆变换：

变换后的参数 满足下列公式：

逆变换后求得的参数N即为寻找的最佳整周模糊度的向量。将求得的整周模糊度固定解带入原双差方程中经最小二乘法求取站间坐标的基线向量，从而获取高精度的位移形变监测数据。

2.2 改进的LAMBDA算法

在LAMBDA算法基础上进行高斯变换及序惯最小二乘，进一步降低协方差的相关性，缩小整周搜索空间。

2.2.1 去相关处理改进

由最小二乘法解得协方差阵Qa和模糊度浮点解a，由于Qa强相关性，通过GAUSS（高斯）变换提高算法效率。设变化后对角阵和下三角阵分别为D’和L’，并要求：D’中元素dn≤….≤dn，L’中元素li,j需尽可能小。相关变化公式如下：

理论上，通过变换后，Qz的相关性较之前有很大提高，整周模糊度搜索空间由扁平狭长区域变化为近似椭球区域。

2.2.2 序惯最小二乘搜索

利用最小二乘法计算残差：

确定搜索范围χ2在离散点上进行模糊度搜索，χ2的选取具有一定经验性，选择过大会造成搜索空间模糊度固定解候选值过大，反之有可能造成搜索不到最佳模糊度，故通过经验值需选取最合适的值。由上式将整周最小二乘估计转化为：基于式（8），建立序惯最小二乘搜索方程：

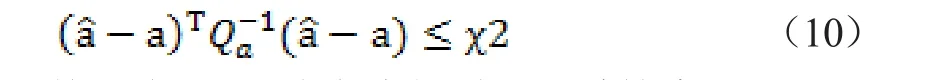
式中，di和lji分别为Qz=L’TDL’的分解对角阵D’和下三角阵L’的相应元素。

由于模糊度之间的相关性，模糊度ai的估值会受到模糊度aj（j=i+1,…,n）的影响，而只有在他们不相关时，才可以得到=。说明ai的区间是以估值为中心，通过序惯条件估计，搜索椭球空间可以获取全部候选整周模糊度，然后通过递归遍历完成序惯最小二乘搜索，最终解算出整周模糊度最优解[6]。

2.3 算法验证

为测试与验证改进的LAMBDA算法的可靠性，以文中的模糊度固定算法为核心，进行测站间的基线解算，利用两块多模多频（北斗：B1/B2，GPS：L1/L2）OEM板卡及两个高精度天线搭建数据采集环境，采集两处的原始数据并在计算机上利用MatLab进行仿真。两处数据采集点：一处选择在某公司12楼楼顶较空旷地域，另一采集点选在某学校主教学楼楼顶，两地距离约4.5千米。数据采集地测试环境良好，视野宽阔，数据采样率为1s。选取其中500个历元，根据本文算法进行解算，将每个历元计算得到的X，Y，Z基线向量与各个分量的平均值做差。如图1所示。

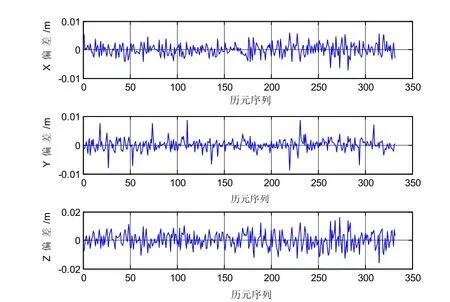
图1 各历元基线向量分量偏差

计算X，Y，Z三个分量的内符合精度σX，σY，σZ。计算公式为：

式中，∆i为各分量计算值与平均值之差；m为观测值个数。计算结果如表1所示。

表1 内符合精度

通过图1和表1可知，利用论文算法在测站都是静态情况下，坐标分量在不同历元下变化较小，坐标各分量内符合精度水平方向和竖直方向在1cm左右，能够满足一般的形变监测要求，且解算效率较高。

上述坐标解算结果求取均值，并与某公司后处理软件进行静态解算结果进行比较：

表2 精度比较

从表2可知，将动态结果与静态解算方法相比，坐标基线向量偏离很小，说明该算例解算结果精确有效。

3 应用案例

利用改进的LAMBDA算法，建设GNSS高精度形变监测平台，通过对形变点长期监测，得到关键参数，并对其进行分析，进而分析和评估安全特性，在实际运行中积累相关数据，获得形变规律，为相关部门提供大数据。形变监测平台架构如图2所示。

图2 形变监测平台架构

平台功能包括数据统计计算、数据分析、超限报警预警等，通过获取实施动态的三维坐标，位移变化状况和振动频率等参数。监测平台数据处理部分包括以下几个步骤：

⊙ 获取站点观测量和星历数据，利用最小二乘平差法解得基线向量浮点解和模糊度浮点解。

⊙ 利用Z变换降低浮点模糊度解相关性，然后利用改进的LAMBDA算法，即使用序惯条件最小二乘和离散搜索策略估算整周模糊度。

⊙ 以确定的整周模糊度为已知量，带入解算方程，求得基线向量固定解。

该系统可以用于建筑物的形变监测、桥梁动态监测、地标沉降、大坝自动化监测及山体滑坡监测等诸多行业领域。建立以GNSS精确测量为核心，获取形变监测大数据，挖掘关乎国际民生的形变数据，分析公共安全领域形变趋势，为相关部门做决策提供数据来源。

4 结束语

论文在研究LAMBDA搜索快速固定整周模糊度方法基础上，对去相关和搜索空间两个方面对LAMBDA算法进行了改进，并利用MATLAB进行仿真实验，实验表明，该种方法在单历元动态解算中快速固定整周模糊度切实有效。同时论文利用GNSS精确动态测量进行形变监测应用分析，建设形变监测平台，快速获取大量数据，这为今后获得海量形变数据，从中挖掘可靠有用的预警与决策信息做下铺垫，也是推广北斗民用化和产业化的重要途径。

[1] 黄张裕，陈苏娟，徐景欣．GPS动态定位中LAMBDA算法的分析及验证[J]．测绘工程，2009,18(6):25-28

[2] 唐卫明，邓辰龙，高丽峰．北斗单历元基线解算算法研究及初步结果[J]．武汉大学学报（信息科学版），2013,38(8):897-901

[3] 祝会忠，高星伟，秘金钟．一种GPS整周模糊度单历元解算方法[J]．测绘科学，2011,36(4):9-11

[4] 阳仁贵，欧吉坤，任超．GPS单历元载波相位整周模糊度的解算方法研究[J]．长江科学院院报，2005,22(1):32-34

[5] P. J. G. Teunissen, The least square ambiguity decorrelation adjustment: a method for fast GPS ambiguity estimation, J. Geodesy, vol.70, 1995

[6] X.W. Chang, X. Yang, and T. Zhou, MLAMBDA: A modified LAMBDA method for integer least‐squares estimation, J. Geodesy, vol.79, 2005

An Improved LAMBDA Algorithm and Its Application in GNSS High Precision Dynamic Solution

Meng Xianwei, Si Tingyong
(Anhui Sun Create Electronics Co., Ltd., Hefei, 230031)

10.3969/J.ISSN.1672-7274.2017.06.003

TN96文献标示码：A

1672-7274（2017）06-0009-03

孟宪伟，男，1980年生，山东曲阜人，博士生，长期从事GNSS接收机系统、授时、导航、高精度测量等领域的研究。吴 伟，深圳市华达玻璃钢通信制品有限公司质量部经理。