GNSS载波相位测量的DGNSS模型── GNSS卫星导航定位方法之八

刘基余

（武汉大学测绘学院，武汉 430079）

GNSS载波相位测量的DGNSS模型── GNSS卫星导航定位方法之八

刘基余

（武汉大学测绘学院，武汉 430079）

差分GNSS载波相位测量，是一种能够获取高精度的卫星导航定位方法，它分为单差法、双差法和三差法，本文论证了它们的数学模型。

差分GNSS(DGNSS)；GNSS载波相位测量；GNSS信号接收机；单差法；双差法；三差法

1 引言

差分GNSS载波相位测量，是一种能够获取高精度的卫星导航定位方法，它分为单差法、双差法和三差法。

2 差分GNSS（DGNSS）载波相位测量

在作差分GNSS（DGNSS）载波相位测量时，假定两台GNSS信号接收机，分别安设在两个不同的测站R和K上，而于两个不同的时元t1和t2，各观测了两颗GNSS卫星（j和n；实际上至少要观测4颗GNSS卫星，此处仅仅为论述简便起见而用之。），则可测得下列8个L1载波相位观测值：

它们分别为（下述式中符号的意义请参阅“GNSS载波相位测量── GNSS卫星导航定位方法之六”一文，《数字通信世界》，2017年第2期，P.1～6）：

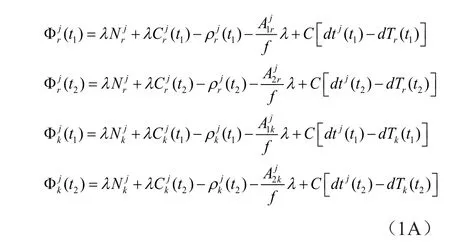
图1 DGNSS动态载波相位测量

依据上列8个L1载波相位观测值，可以组成下列三种差分测量值：

2.1 四个单差分测量值

图2表示在测站之间进行求差解算。依据上列8个L1载波相位测量观测值，可以求得如下所述的单差分测量值。

图2 站际单差分测量示意

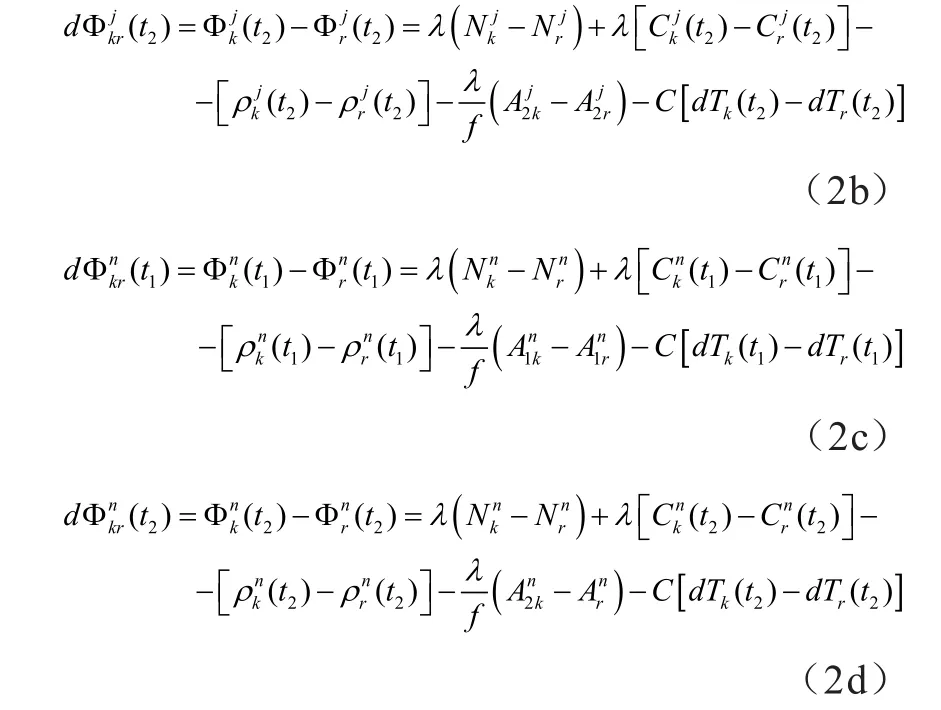
从上列方程可见，单差法，是两台分别安设在两个测站上的GNSS信号接收机（K，R），于同一时元对同一颗GNSS卫星的载波相位测量进行求差；这种在两台接收机之间进行载波相位测量求差解算，简称为“站际单差”。也可在两颗GNSPS卫星之间进行载波相位测量求差解算，称之为“星际单差”。站际单差的优点是，消除了星钟误差和星历误差。

2.2 二个双差分测量值

图3 双差分测量示意

图3表示在测站和卫星之间进行求差解算。依据上列8个L1载波相位测量观测值，可以求得如下所述的双差分测量值。

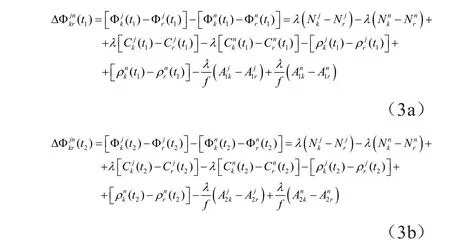
从上列方程可见，双差法是两台分别安设在两个测站上的GNSS信号接收机（K，R），于同一时元对两颗不同的GNSS卫星的载波相位测量进行求差，即，双差法是同一时元的两个单差测量值之差。其优点是，除了消除了星钟误差和星历误差以外，还消除了两台GNSS信号接收机的星钟误差。因此，双差法能够显著地提高GNSS卫星导航定位精度，而被广泛应用之。

2.3 一个三差分测量值

图4表示在测站、卫星和时元之间进行求差解算。依据上列8个L1载波相位测量观测值，可以求得如下所述的三差分测量值。

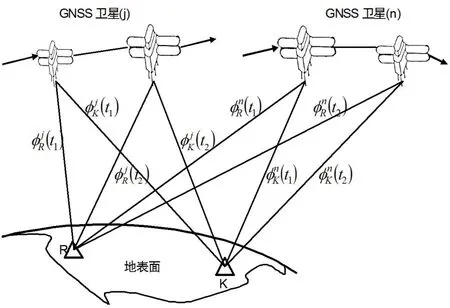
图4 三差分测量示意

从上列方程可见，三差法是两台分别安设在两个测站上的GNSS信号接收机（K，R），于不同的时元(t1，t2)对两颗不同的GNSS卫星(j，n)的载波相位测量进行求差。即，三差法是不同时元、不同卫星的两个双差测量值之差。其优点是，不仅消除了星钟误差、星历误差和GNSS信号接收机钟差，而且消除了波数（整周模糊度；如表1所示）。

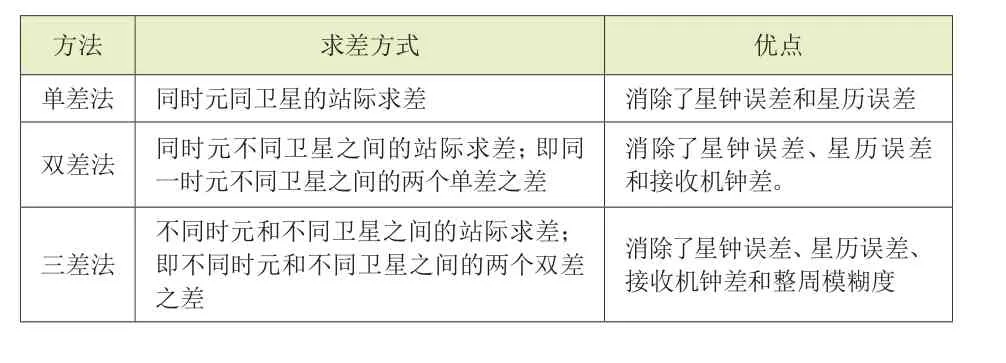
表1 DGNSS测量的优越性

GNSS载波相位测量的三差法，还可用于周跳的修除。例如，若在观测GNSS卫星j和n时，仅对GNSS卫星j作载波相位测量时，测站K上发生了周跳（CS），而获得了如表2所示的载波相位测量观测值。仅以这5个时元的载波相位测量观测值而求得如表3的单差、双差和三差等三种差分测量值。

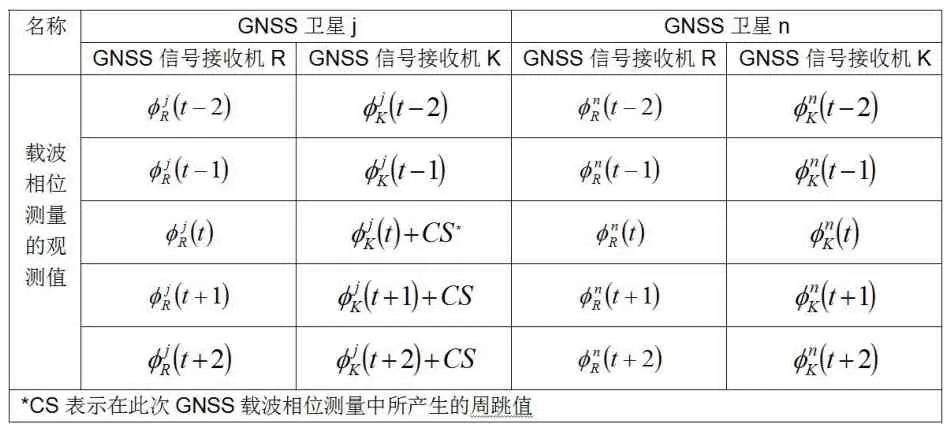
表2 两颗卫星（j，n）的载波相位测量观测值

表3 单差、双差和三差差分测量值

从表3可见，在5个双差测量值中，有3个双差测量值存在周跳；而在4个三差测量值中，只有一个三差测量值存在周跳。因此，我们可以利用无周跳的三差测量值，精确地解算出基线向量，进而修除周跳，再作整体解算。

在上述求差解算时，一般选用一颗高度角较大的GNSS卫星作为求差的参考卫星，进而用其他3颗以上GNSS卫星的载波相位测量观测值，与参考GNSS卫星的载波相位测量观测值进行求差，而获得所需要的差分测量值。不管是GNSS静态定位，还是GNSS动态测量，载波相位测量观测值的求差解算，均能够获得较高的导航定位精度；现以GPS为例，说明能够获精度增益如表4所示。

表4 DGPS动态定位精度

着陆是飞机安全飞行的关口阶段，它包括起始进场、下滑和拉平三个过程，每一个过程要求不同的二维位置/垂直精度。根据国际民用航空组织（ICAO）于1998年8月对GNSS用于进近着陆的建议标准为：

⊙ I类精密进近的二维位置/垂直精度是16.0m/4.0m。

⊙ I I类精密进近的二维位置/垂直精度是6.5m/1.7m。

⊙ III类精密进近的二维位置/垂直精度是3.9m/0.8m。

这与V.Sankaran和D.Benson两位学者所推荐的精度要求相符合，其详情如表5所示。

从以上表格可见，用机载GPS载波相位测量平滑DGPS伪距解，基本上可以达到飞机的III类精密进近着陆的精度要求；若用GNSS动态载波相位测量求差解算，则可确保飞机的III类精密进近着陆的精度要求。

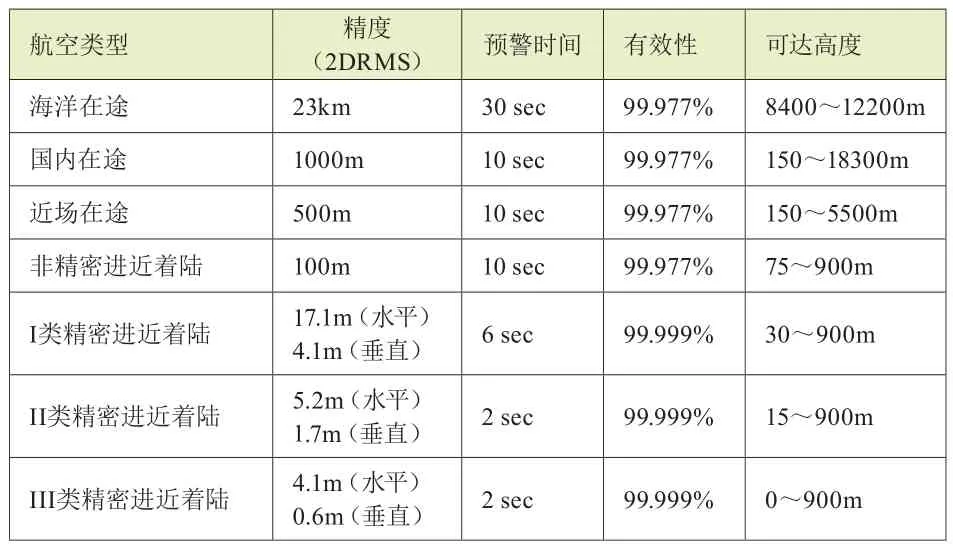
表5 航空导航/定位的要求精度

3 组合测量与GNSS测量

2008年初春，在加拿大的GPS/GLONASS/ EGNOS组合观测的试验表明，对于几米长的短基线而言，相对定位测量的单一GPS伪距/载波相位测量解算的三维坐标误差，大于GPS/GLONASS/ EGNOS组合伪距/载波相位测量解算的三维坐标误差；然而，GPS/GLONASS/EGNOS组合伪距/载波相位测量解算的三维坐标误差与GPS/GLONASS组合伪距/载波相位测量解算的三维坐标误差相差甚小（详见表6所示）。换言之，GNSS测量精度，是否比双星座（如GPS/GLONASS）组合测量精度高许多，有待验证之！

表6 GPS/GLONASS/EGNOS组合在6m基线上的伪距/载波相位测量解算成果比较

载波相位差分测量的基准站设置和DGNSS数据链等问题，请参阅“GNSS伪距差分定位及其特色── GNSS卫星导航定位方法之二”一文（《数字通信世界》，2016年第8期，P.1～6）

[1] 刘基余，全球导航卫星系统及其应用，北京测绘出版社，2015年5月

[2] Lachapelle,G., GPS Theory and Applications, University of Calgary, Fall 2000, PP.310

DGNSS Model of GNSS Carrier Phase Measurements --Method of GNSS Navigation/Positioning (8)

Liu Jiyu
(School of Geodesy and Geomatics, Wuhan University, Wuhan, 430079)

GNSS carrier phase differential measurements are a kind of satellite navigation/positioning method which can obtain high navigation/positioning accuracy. It can be divided into single differential method, double differential method and three differential method. In this paper their mathematical models are demonstrated.

Differential GNSS; GNSS carrier phase differential measurements; GNSS signal receiver; Single differential method; Double differential method; Three differential method

10.3969/J.ISSN.1672-7274.2017.06.001

TN96

A

1672-7274（2017）06-0001-04

刘基余，现任武汉大学测绘学院教授/博士生导师，兼任美国纽约科学院（New York Academy of Sciences）外籍院士、中国电子学会会士。主要研究方向是GNSS卫星导航定位/卫星激光测距技术，在国内外30余种中英文学术期刊上发表了280余篇相关研究论文，独著了（北京）科学出版社于2013年1月出版发行的《GPS卫星导航定位原理与方法》一书。他的主要业绩已分别载于美国于2001年出版发行的《世界名人录》（Who's Who in the World）、美国于2005年出版发行的《科技名人录》（Who's Who in Science and Engineering）和中国科学技术协会于2007年出版发行的《中国科学技术专家传略》工程技术编《电子信息科学技术卷2》等50多种国内外辞书上。