试验设计类型之可以考察全部交互作用的多因素设计：析因设计

谷恒明，胡良平,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

科研方法专题

试验设计类型之可以考察全部交互作用的多因素设计：析因设计

谷恒明1，胡良平1,2*

(1.军事医学科学院生物医学统计学咨询中心，北京 100850；2.世界中医药学会联合会临床科研统计学专业委员会，北京 100029

本文目的是介绍一种可以考察各级交互作用的多因素设计类型，即析因设计。通过介绍两个实际例子，总结出析因设计的八个特点及优点、缺点。针对实际应用时可能面临的情况或问题，人们可能会对析因设计进行改造，由此产生了析因设计的三种变形，即“含区组因素的析因设计”“分式析因设计”和“多因素非平衡组合试验”。最后一种情形，是实际工作者常会使用的，但在对定量评价指标进行差异性分析时需要对原先的分组进行合理拆分，再进行恰当的组合，构造出多种标准的设计类型，以利于分析者选择正确的统计分析方法。

试验因素；区组因素；析因设计；分式析因设计；交互作用

1 概 述

具有正常思维和心理的人做任何事都会通盘考虑，尽可能做到系统全面、有条不紊。然而，对于一个事物而言，在众多的设计类型之中，“析因设计”就具有前述提及的那种“潜质”。

析因设计具有多个特点，其中最突出的特点是包括全部的“试验点(即试验因素不同水平组合所决定的每个特定试验条件)”数目，是全部拟被考察的试验因素水平的全面组合数。例如，假定在某项试验研究中共需考察10个三水平试验因素，若采用析因设计，则全部试验点数为310=59 049个。这个数目代表什么含义呢？它相当于科研人员习惯上所称呼的“试验分组数”。若每个试验组仅做一次试验(即无重复试验)，那这个数也可以被叫做“总试验次数”。但是，此时的安排不能被称为“十因素析因设计”，而只能被称为“无重复试验的十因素全面组合试验”。因为由这样的安排得出的试验结果不能全面、真实地揭示多个试验因素各自和相互作用对结果产生的影响，即使采用某种复杂的统计分析方法，也可能会得出错误的结论。原因在于：试验结果中没有包含试验因素对评价结果的作用规律，全靠统计学或数学方法是不可能创造出规律来的。

2 析因设计实例

2.1 两因素析因设计实例

【例1】观察A、B两种镇痛药物联合运用在产妇分娩时的镇痛效果。A药取3个剂量：1.0 mg，2.5 mg，5.0 mg；B药也取3个剂量：5 μg，15 μg，30 μg。共9个处理组。将27名产妇随机等分为9组，每组各3名，记录每名产妇分娩时的镇痛时间，结果见表1。试分析A、B两种药物的联合镇痛效果[1]。

表1 A、B两种药物联合运用的镇痛时间(min)

2.2 三因素析因设计实例

【例2】某临床医生收集到如下资料[2]，见表2。问：此资料所对应的试验设计类型是什么？

3 实例解析

3.1 对例1的解析

在例1中，有两个独立于受试对象(本例中为产妇)的试验因素，分别叫做“A药剂量”与“B药剂量”，它们都具有3个水平。每位产妇均需同时接受两种镇痛药以减轻分娩时的疼痛，由基本常识可知，在使用时，每种镇痛药只可能取一个特定的剂量，于是，两种镇痛药的剂量组合数就有3×3=9种(即试验点数)。在各种组合(即试验点或称特定的试验组)下均做了3次独立重复试验(即有三位产妇)。有一个定量的评价指标，即“镇痛时间(min)”,确切地说，应该是“镇痛保持的时间(min)”。

临床医生并没有声明：所涉及的两个试验因素对评价指标的影响是否有主次之分，只能被视为“同等重要或地位平等”。

基于以上的背景，可以比较有把握地判定例1的试验安排属于“两因素析因设计”。

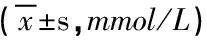
表2 2 545例糖尿病患者血脂检测结果

注：TC，总胆固醇；TG，甘油三酯；HDL-C，高密度脂蛋白胆固醇；LDL-C，低密度脂蛋白胆固醇

3.2 对例2的解析

在例2中，表2中的“组别”究竟是一个8水平的因素，还是多个因素的组合呢？仔细观察“组别”之下的8行内容，不难发现：它们是“C高否”“G高否”与“HD低否” 3个因素各2水平的全面组合而得到的，即这是由3个2水平试验因素按2×2×2组织起来的“架构”。表2中的后4列为在临床上可能有联系的4个定量指标，若需要同时考察它们的变化情况，就属于四元统计分析问题，它们不影响对设计类型的判定。

若将表2中的第1列改写成3列，即把3个试验因素的名称及其水平各用一列来呈现，就把一个貌似“单因素8水平”的“混淆型设计架构”清楚地“重构”了，使其成为一个“2×2×2”的“设计架构”，见表3。

此时，仅依据表3的外表，还不能直接判定其为“三因素析因设计”。还必须声明：这3个因素对评价指标(这里有4个定量评价指标)的影响是否“地位平等”，仅当答案为“以专业知识为依据，3个因素对所有定量评价指标的影响地位平等”时，表3所对应的安排才可以被叫做“三因素析因设计”或“2×2×2析因设计”。后一种称呼稍好一点，因为它清楚地告知读者，每个因素有几个水平。

表3 用三因素及其水平组合取代表2中“组别”±s，mmol/L)

4 析因设计的特点

在文献[3]中，呈现了析因设计具有的7个特点。为严谨起见，这里还要补充一点，汇总如下。

具备下列8个特点的多因素试验设计可被称为标准的析因设计：①试验因素个数≥2；②每个试验因素的水平数≥2且可以不相等；③试验因素之间不存在“连带关系”且独立于受试对象；④不同的试验条件数(或组合数、试验点数)等于全部试验因素的水平数之乘积；⑤各试验条件下至少要做两次独立重复试验；⑥全部受试对象被完全随机地分配到任何一个试验条件组中去，各小组中的受试对象个数可以不等，但最好相等；⑦试验时，任何一次试验都将涉及到任何一个试验因素的某个水平，即全部试验因素同时施加；⑧进行统计分析时，假定有专业依据认为：全部试验因素对观测结果的影响是地位平等的，即没有主次之分。

由上述特点，决定了析因设计具有明显的优点和缺点。优点：可以分析每个试验因素的主效应和试验因素之间各级交互作用的效应大小。缺点：总试验次数太多，试验费用大且费时费力。

若严格按上述的8个特点来考察，例2不满足上述的“第三点”和“第六点”。因此，例2中的表3确实具有“析因设计结构”，但算不上“标准的析因设计”。相比而言，例1中的表1可称为“标准的两因素析因设计”。

说明：上述“第三个特点”中的“连带关系”是指一个因素与另一个因素之间存在内在的联系，例如，药物种类(分为A药、B药)与“药物剂量”之间就存在“连带关系”。假定在本文例1中，每个产妇只接受一种特定剂量的镇痛药，全部产妇被随机分配到6个试验组，分别为A药的3个剂量组与B药的3个剂量组。这样的安排，很容易被判定为2×3析因设计(药物种类有2个水平，药物剂量有3个水平)。若考虑到两个因素之间存在“连带关系”，将其判定为两因素嵌套设计更为合理。

5 析因设计的变形

5.1 含区组因素的析因设计[4]

【例3】有人研究猪食用不同饲料对体重增加量的影响。A(大豆粉+不同含量的蛋白质)：A1(加14%蛋白质)、A2(加12%蛋白质)；B(玉米中己氨酸的含量)：B1(含0.6%己氨酸)、B2(缺乏己氨酸)，共有4种不同的饲料配方。用24头猪作为受试对象，按猪的初始体重由轻到重排序，并形成6个随机区组，每组中的4只猪体重接近，被随机分到4个饲料组中，在喂养期间，尽可能使每只猪每餐都能吃饱。设计格式和资料见表4，该资料所取自的试验设计类型为含区组因素的析因设计。

表4 两种饲料的不同配方对猪平均日增重量的影响结果

【分析与解答】在表4中，核心架构是由A、B两个试验因素组成的2×2析因设计，在将受试对象(本例为猪)分组时，将其“原始体重”作为一个重要的非试验因素。由于“原始体重”是定量因素，又按范围将其划分成6段，使其转化成“有序因素”。于是，就派生出一个所谓的“区组因素”。考虑区组因素的目的是尽可能消除“原始体重”对评价指标(平均日增重量)的影响，更真实地显露出试验因素不同水平组合所决定的试验条件(在本例中，本质上是营养价值高低)对评价指标的影响大小。

5.2 分式析因设计[4-6]

【例4】25-1分式析因设计：若有5个2水平试验因素，析因设计的水平组合数为32种，基于5因素的交互作用项的正、负号，可将32种组合一分为二，取其中一半所对应的水平组合，就称为分式析因设计。

【分析与解答】若设每个试验因素的水平分别为-1与1，则在五个2水平因素的32种水平组合中，取五个因素的水平连乘积为“+1”或“-1”的部分，即16种水平组合，见图1(五因素交互作用取“+1”的那部分，图中Y之下填写试验结果)。

OBSYX1X2X3X4X51。111-1-12。-1-1-1-113。1-1-1114。1-1-1-1-15。1-11-116。-111-117。1-111-18。111119。-1111110。-1-1-11-111。-11-1-1-112。-1-11-1-113。-1-111114。11-1-1115。-11-11116。11-11-1

图1 25-1分式析因设计对应的水平组合

同理，25-1分式析因设计、25-2分式析因设计，一般用符号表示如下：2P-K分式析因设计，其中P>K，皆为正整数。

同理，34-1分式析因设计、34-2分式析因设计，一般用符号表示如下：3P-K分式析因设计，其中P>K，皆为正整数。

5.3 不平衡析因设计——多因素非平衡组合试验[2]

【例5】沿用例1资料，假定研究者在下列三种条件下，未做试验：①：A(1.0)与B(5)；②：A(2.5)与B(15)；③：A(5.0)与B(30)。

试辨析这是一个什么试验设计类型。

【分析与解答】在一个析因设计中，少做了一组或多组试验，其安排就不能被称为析因设计了。从表面上看，它属于“不平衡析因设计”。其实，它已经严重偏离了“标准析因设计的定义或特点”。它的最确切名称为“多因素非平衡组合试验”，因为它已经没有“资格”被称为“设计”了。对基于这种安排而产生的定量评价指标的数据拟做差异性分析之前，首先必须对全部试验组进行合理的拆分；然后再结合基本常识、专业知识和统计学知识进行各种重新组合，这个过程相当于进行“回顾性试验设计”。根据不同的组合判断其应属于什么试验设计类型，再选用相应的差异性分析模型对定量资料进行分析，具体方法参见文献[2-3]，此处从略。

[1] 胡良平，王素珍，郭晋. 内科科研统计设计与数据分析[M]. 北京: 电子工业出版社，2015: 33-39.

[2] 胡良平. 统计学三型理论在实验设计中的应用[M]. 北京：人民军医出版社，2006: 152-163.

[3] 胡良平. 科研设计与统计分析[M]. 北京: 军事医学科学出版社，2012: 228-264.

[4] 胡良平. 面向问题的统计学——(1)科研设计与统计基础[M]. 北京: 人民卫生出版社，2012:166-219.

[5] 郭祖超. 医用数理统计方法[M]. 3版. 北京: 人民卫生出版社，1988: 307-341.

[6] Dean A, Voss D. Design and analysis of experiments[M]. New York: Springer, 1999: 483-546.

(本文编辑：吴俊林)

科研方法专题策划人——胡良平教授简介

胡良平，男，1955年8月出生，教授，博士生导师，曾任军事医学科学院研究生部医学统计学教研室主任和生物医学统计学咨询中心主任、国际一般系统论研究会中国分会概率统计系统专业理事会常务理事和北京大学口腔医学院客座教授；现任世界中医药学会联合会临床科研统计学专业委员会会长、中国生物医学统计学会副会长，《中华医学杂志》等10余种杂志编委和国家食品药品监督管理局评审专家。主编统计学专著45部，参编统计学专著10部；发表第一作者学术论文220余篇，发表合作论文130余篇，获军队科技成果和省部级科技成果多项；参加并完成三项国家标准的撰写工作；参加三项国家科技重大专项课题研究工作。在从事统计学工作的30年中，为几千名研究生、医学科研人员、临床医生和杂志编辑讲授生物医学统计学，在全国各地作统计学学术报告100余场，举办数十期全国统计学培训班，培养多名统计学专业硕士和博士研究生。近几年来，参加国家级新药和医疗器械项目评审数十项、参加100多项全军重大重点课题的统计学检查工作。归纳并提炼出有利于透过现象看本质的“八性”和“八思维”的统计学思想，独创了逆向统计学教学法和三型理论。擅长于科研课题的研究设计、复杂科研资料的统计分析与SAS实现、各种层次的统计学教学培训和咨询工作。

Types of the multifactor experimental designs with all interactions: factorial design

GuHengming1,HuLiangping1,2*

(1.ConsultingCenterofBiomedicalStatistics,AcademyofMilitaryMedicalSciences,Beijing100850,China; 2.SpecialtyCommitteeofClinicalScientificResearchStatisticsofWorldFederationofChineseMedicineSocieties,Beijing100029,China*Correspondingauthor:HuLiangping,E-mail:lphu812@sina.com)

The paper aims to introduce a multifactor design type that can examine the interactions at all levels, that is factorial design. By introducing two practical examples, the eight characteristics and advantages and disadvantages of the factorial design are summarized. Facing the situation or the problem in the real application, people may transform the factorial design into the following three forms: factorial design with block factor, fractional factorial design and multifactor unbalanced combination test. The last case is often used by the actual workers. However, the primary task is to reasonable divide the original grouping and then appropriate combination in the difference analysis for quantitative evaluation index. Thus, a variety of standard design types are constructed and facilitate the analysts to select a correct statistical analysis.

Experimental factors; Block factor; Factorial design; Fractional factorial design; Interaction effection

R195.1

A

10.11886/j.issn.1007-3256.2017.03.001

国家高技术研究发展计划课题资助(2015AA020102)

2017-06-04)

*通信作者：胡良平，E-mail：lphu812@sina.com)