装配式简支T梁宽桥横向分布

苏 佩, 钱若霖, 邬晓光, 贺 攀(长安大学 公路学院, 陕西 西安 710064)



装配式简支T梁宽桥横向分布

苏 佩, 钱若霖, 邬晓光, 贺 攀
(长安大学 公路学院, 陕西 西安 710064)

以宽跨比0.625的装配式简支T梁为依托,分别采用梁格法和实体单元建模方式分析了中载和偏载两种工况下跨中截面应力及挠度分布,得出小宽跨比宽桥梁格法建模是满足精度的.利用梁格法反算横向分布系数与传统理论G-M法进行对比,得出G-M法对于中梁适用,而对于边梁误差较大的结论,在宽桥设计计算时应重点考虑.

桥梁工程; 宽跨比; T梁;宽桥; 横向分布; 梁格法

随着经济的迅速发展,人流量和车流量日益增加,为保证交通的快捷顺畅,宽桥在桥梁建设中的应用也越来越广泛,尤其是装配式T梁和小箱梁宽桥[1]以其安全便捷、施工质量高的特点得到桥梁设计者青睐.一般认为宽跨比(B/L)大于等于0.5的桥梁为宽桥,目前研究多以窄桥为主[2-3],其中已有的理论方法有刚性横梁法和G-M法.刚性横梁法把梁桥视作由主梁和横梁组成的梁格系,载荷通过横梁由一片主梁传到其他主梁上,同时主梁又对横梁起弹性支承作用;G-M法把结构简化为纵横相交的梁格系,按杆件系统的空间结构来求解,也可设法把结构简化为一块矩形的平板,作为弹性薄板理论进行分析.随着宽跨比的增大,很多问题相应而生,针对宽桥横向分布的研究逐渐得到人们的重视[4],宽桥横向分布、稳定等方面都和窄桥有很大区别,呈现出显著的空间效应[5-6].对宽桥进行整体的空间分析得出其横向分布规律对其设计优化和安全性能具有很大意义.本文采用梁格法[7-8]和实体单元[9-10]建模两种方法分别对比分析了装配式T型宽桥主梁的横向分布特性,以得到更适合宽桥建模的方法以及力学特性.

1 工程概况及计算模型

本文以某20 m预应力简支T梁宽桥为工程背景,桥梁宽度12.5 m,由5片T梁组成,跨径20 m,桥梁宽跨比为B/L=0.625,截面形式如图1、图2所示,主梁采用C50混凝土.本文采用midas/civil建立梁格法有限元模型,采用ANSYS建立实体单元模型,主要进行主梁的模拟,通过主梁的挠度响应反算横向分布特性进行研究分析.

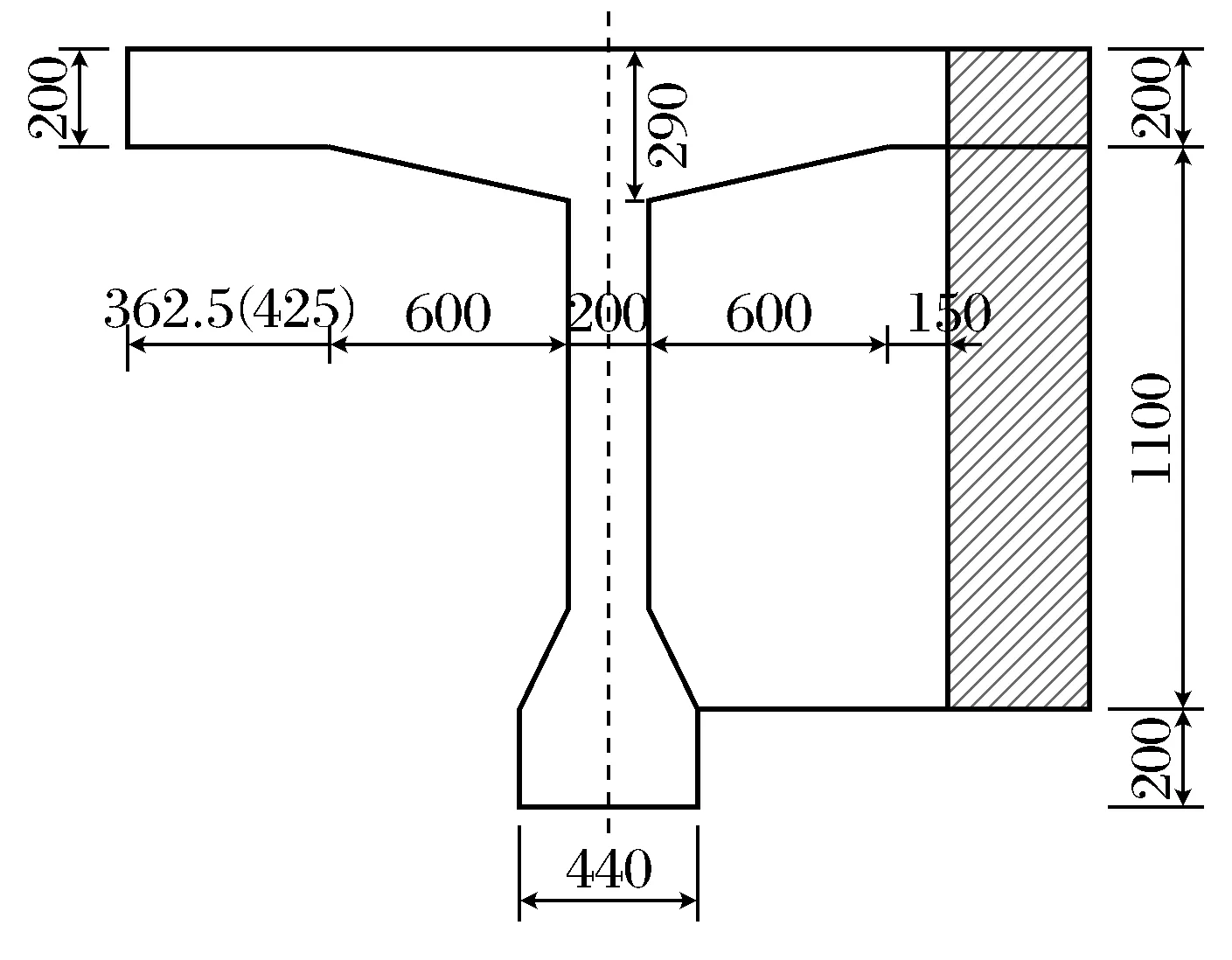
图1 边梁截面Fig.1 The section of side beam

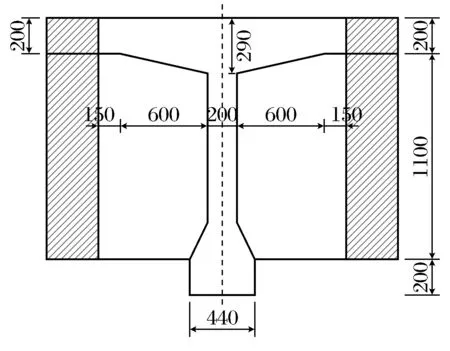
图2 中梁截面Fig.2 The section of middle beam

2 简支T梁宽桥横向受力分析

2.1 计算工况的选取

考虑到简支T梁宽桥横向主梁数量一般较多,宽度较大,空间受力情况较窄桥有差异.为得到宽桥的应力及变形整体受力性能,借助midas/civil梁格法有限元模型和ANSYS实体单元模型对比分析,分别选取计算工况如下.

工况1:中载,集中载荷100 kN作用于跨中中梁处.

工况2:偏载,集中载荷100 kN作用于跨中边梁处.

2.2 应力、挠度的对比分析

利用midas/civil梁格法建模并查看其两种工况下的应力及挠度图,如图3 ～图6所示.

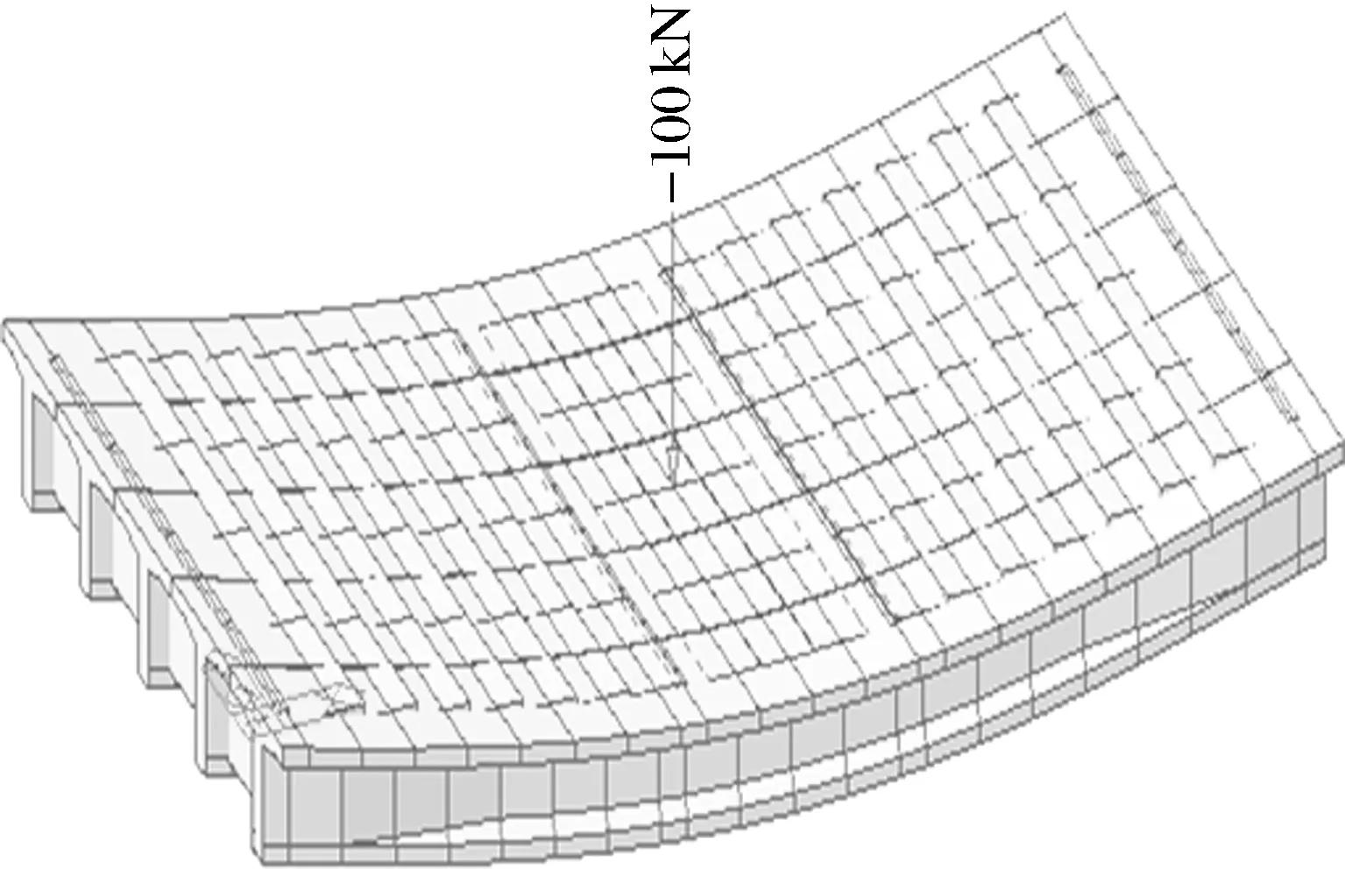
图3 梁格法工况1挠度图Fig.3 Deflection diagram under beam grid method 1

图4 梁格法工况1应力图Fig.4 Stress diagram under beam grid method 1

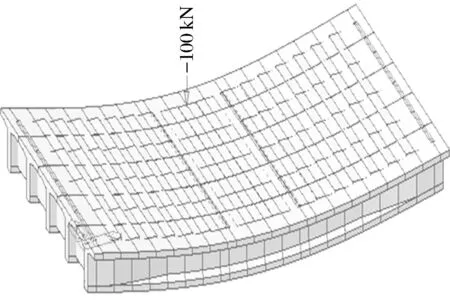
图5 梁格法工况2挠度图Fig.5 Deflection diagram under beam grid method 2

图6 梁格法工况2应力图Fig.6 Stress diagram under beam grid method 2

提取跨中截面底板应力及梁底挠度数据如表1所示.

表1 Midas/civil梁格模型两种工况下应力及变形值Table 1 Stress and deformation values under beam grid method

与梁格法建模思路相似,利用ANSYS实体单元建立全桥模型并查看不同工况下应力及挠度云图,如图7 ～图10所示.

图7 实体建模工况1挠度图Fig.7 Deflection diagram under solid modeling 1

图8 实体建模工况1应力图Fig.8 Stress diagram under solid modeling 1

提取跨中截面最大应力及梁底挠度数据如表2所示:

比较两种建模方式及各工况下跨中特征截面应力及挠度值,变化规律如图11～图12所示.由图3～图12及表1、表2可知:

表2 ANSYS实体模型两种工况下应力及变形值Table 2 Stress and deformation values under solid modeling ANSYS

图9 实体建模工况2挠度图Fig.9 Deflection diagram under solid modeling 2

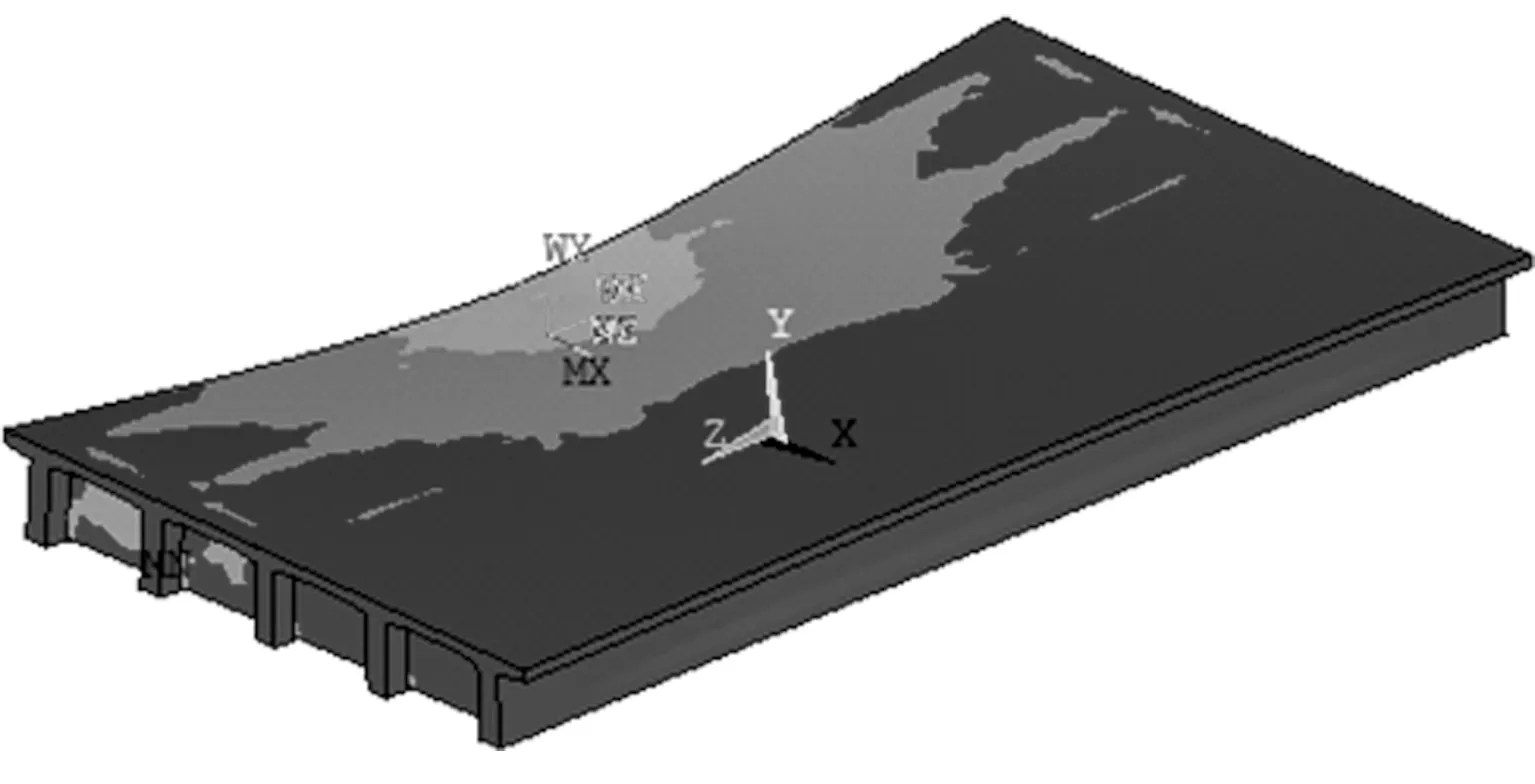
图10 实体建模工况2应力图Fig.10 Stress diagram under solid modeling 2

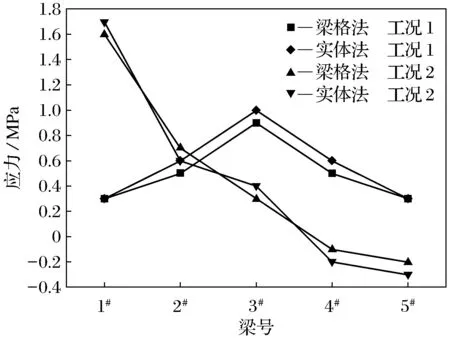
图11 应力变化规律Fig.11 Stress variation law

(1) 两种建模方式中载工况下应力挠度均呈对称分布,集中载荷作用的梁应力挠度最大;

(2) 对于该宽桥结构,偏载工况下中梁应力挠度大于中载工况下边梁的应力挠度.偏载工况下另一片边梁挠度出现正值.由此可见,梁间横向传力作用对于宽桥影响是显著的,在设计计算时应予以重视.

(3) 两种建模方式所得应力挠度值误差很小,理论上采用实体建模方法分析宽桥结构更精确,但实体建模复杂繁琐;梁格法建模方便快捷,且对于小宽跨比的宽桥精度满足精度要求.

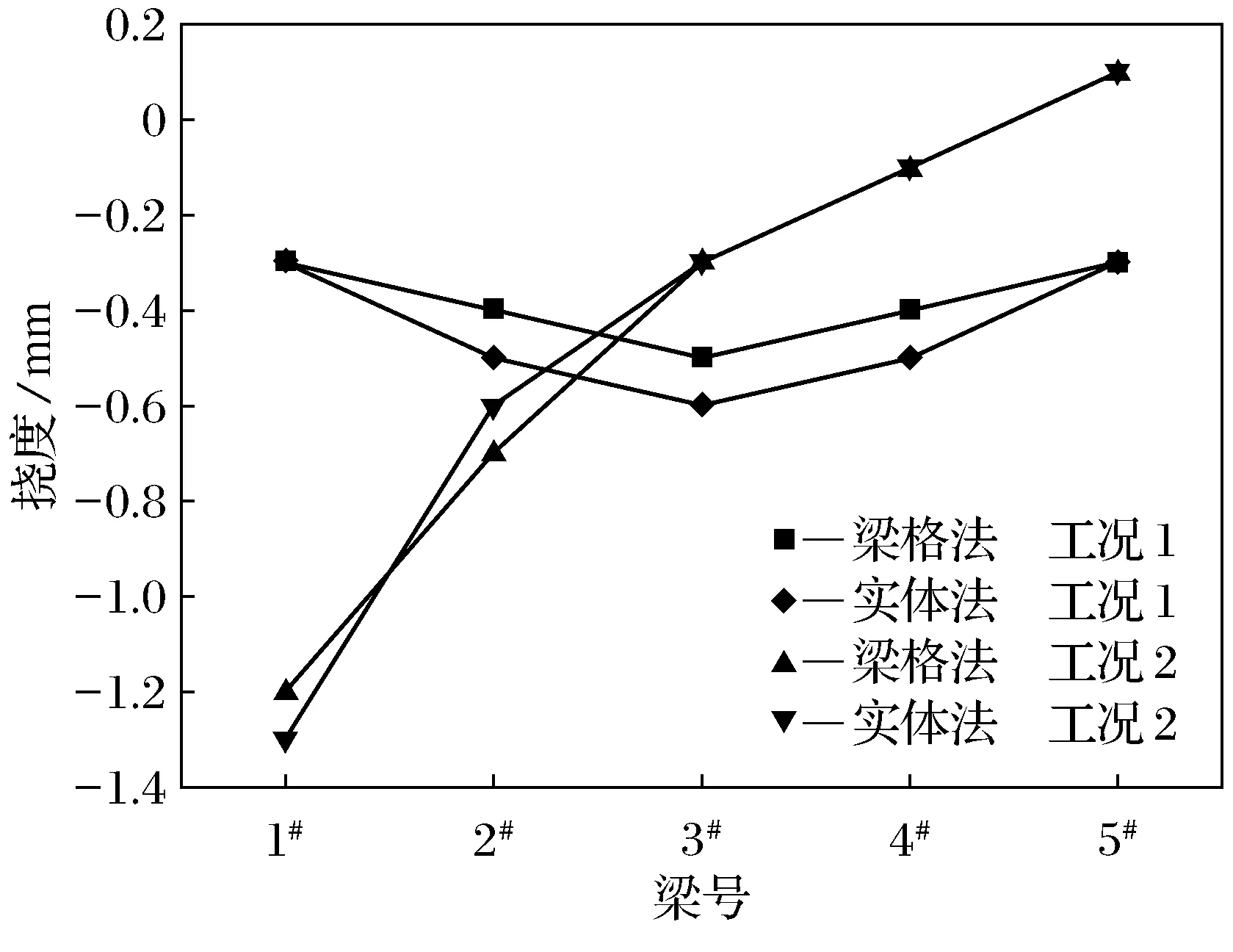
图12 挠度变形规律Fig.12 Deformation variation law

3 横向分布系数计算

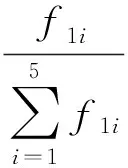
根据G-M法截面参数计算并查表以及根据挠度值反算横向分布系数结果如表3所示.

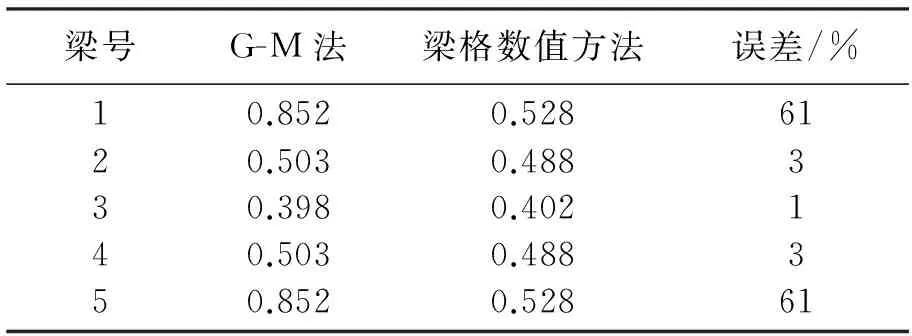
表3 G-M法与梁格数值方法横向分布系数及误差

由表3中数据对比可见,对于简支T梁宽桥桥横向分布系数的计算,GM法计算边梁时所得横向分布系数较大,误差达到61%,但在计算中梁时与梁格数值方法结果较接近,误差最大3%,具有一定精度.故采用GM法计算宽桥中梁横向分布系数,与实际较吻合.对于边梁横向系数的计算采用梁格数值方法较为精确.

4 结 论

(1) 在对宽跨比为0.625但不大于1的小宽跨比装配式简支T梁宽桥进行受力分析时,采用梁格法建模满足精度要求,根据计算需要可以考虑复杂的实体建模方法.

(2) 宽桥的横向传力规律不同于窄桥,其空间效应明显,传统理论方法存在局限,在设计计算时应考虑其影响,建立整体空间模型计算其横向分布.

(3) G-M法计算装配式简支T梁宽桥横向分布时,对于边梁不再适用,但对于中梁误差在3%以内,具有一定精度.

[ 1 ] 陈双聪,陈勇,吴涛. 装配式小箱梁宽桥横向分布计算方法研究[J]. 华东公路, 2016(2):5-7. (CHEN S C,CHEN Y,WU T. Study on calculation method of lateral load distribution of assembled box girder wide bridge[J]. East China Highway, 2016(2):5-7.)

[ 2 ] 张晓光,韩楠楠. 国内外桥梁横向分布系数计算方法讨论[J]. 甘肃科技, 2011,27(7):130-132. (ZHANG X G,HAN N N. Discussion on calculating method of lateral load distribution coefficient of bridges at home and abroad[J]. Gansu Science and Technology, 2011,27(7):130-132.)

[ 3 ] 杨年芳. 宽桥横向分布系数的精确快速计算方法[J]. 湖南交通科技, 2011,37(2):85-88. (YANG N F. Accurate and fast calculation method for lateral load distribution coefficient of wide bridge[J]. Hunan Communication Science and Technology, 2011,37(2):85-88.)

[ 4 ] 钱寅泉,周正茂,王素娟,等. 装配式小箱梁桥载荷横向分布数值分析与试验[J]. 公路交通科技, 2012,29(1):86-90. (QIAN Y Q,ZHOU Z M,WANG S J,et al. Numerical and experiment of lateral load distribution of fabricated small box girder bridge[J]. Journal of Highway and Transportation Research and Development, 2012,29(1):86-90.)

[ 5 ] 向中富,王家林,孙淑红,等. 箱拱桥载荷横向分布计算的比拟板法研究[J]. 公路交通科技, 2006,23(6):72-76. (XIANG Z F,WANG J L,SUN S H,et al. Study on the calculation of lateral load distribution of box arch bridge by the analogy plate method[J]. Journal of Highway and Transportation Research and Development, 2006,23(6):72-76.)

[ 6 ] 聂鑫,樊健生,付裕. 箱形截面连续组合梁桥的载荷横向分布[J]. 清华大学学报(自然科学版), 2009(12):1930-1933. (NIE X,FAN J S,FU Y. Lateral load distribution of box girder continuous composite beam bridge[J]. Journal of Tsinghua University(Science and Technology), 2009(12):1930-1933.)

[ 7 ] 李乐秋,彭斌,李勇. 城市宽桥横向分布系数采用梁格法的计算探讨[J]. 中国市政工程, 2009(2):31-31. (LI L Q,PENG B,LI Y. Calculation of lateral load distribution coefficient of city wide bridge by beam grid method[J]. China Municipal Engineering, 2009(2):31-31.)

[ 8 ] 王仕实,孙卓,蔡卡宏,等. 基于梁格法在用简支梁桥载荷横向分布应用研究[J]. 广州大学学报(自然科学版), 2012,11(5):56-60. (WANG S S,SUN Z,CAI K H,et al. Research on lateral load distribution of simple supported beam bridge based on grillage method[J]. Journal of Guangzhou University(Natural Science Edition), 2012,11(5):56-60.)

[ 9 ] 吴炜,翁洋,吕建鸣. 用ANSYS对T梁和空心板梁桥进行结构仿真分析的研究[J]. 公路交通科技, 2004,21(6):69-72. (WU W,WENG Y,LYU J M. Study on Structural Simulation Analysis of T beam and hollow slab beam bridge by ANSYS[J]. Journal of Highway and Transportation Research and Development, 2004,21(6):69-72.)

[10] 林文思,黄永辉. 一种改进的T梁载荷横向分布系数计算方法[J]. 广东公路交通, 2007(3):29-33. (LIN W S,HUANG Y H. An improved calculating method of lateral load distribution coefficient of t beam load[J]. Guangdong Highway Communications, 2007(3):29-33.)

【责任编辑: 赵 炬】

Transverse Distribution of Fabricated Simply Supported T-Girder Bridge

SuPei,QianRuolin,WuXiaoguang,HePan

(School of Highway, Chang’an University, Xi’an 710064, China)

The beam-grid method and the solid element method are used to analyze the stress and deflection distribution of the mid-span section under the loading condition and the eccentric load condition, respectively, based on the simply supported T-beam with the span ratio 0.625. The beam grid method is to meet the precision for modeling of wide bridge in small wide-span ratio. It is found that G-M method is suitable for middle beam, while for the conclusion that the side beam error is large, it should be considered in the design of wide-span bridge again when the lateral load distribution coefficient is compared with the traditional theoretical G-M method by using beam grid numerical method.

bridge engineering; width-span ratio; T-beam; wide bridge; lateral load distribution; beam grid method

2016-12-08

苏 佩(1993-),女,长安大学硕士研究生人; 邬晓光(1961-),男,湖北英山人,长安大学教授,博士生导师.

2095-5456(2017)03-0229-04

U 443.3

A