大跨径连续刚构桥混凝土合理加载龄期

黄叙钦, 李艺林, 安平和, 郑 鹏(长安大学 桥梁与隧道陕西省重点实验室, 陕西 西安 710064)



大跨径连续刚构桥混凝土合理加载龄期

黄叙钦, 李艺林, 安平和, 郑 鹏
(长安大学 桥梁与隧道陕西省重点实验室, 陕西 西安 710064)

为分析混凝土的收缩徐变对大跨度连续刚构桥在运营阶段受力性能的影响,通过统计分析陕西地区已建成的大跨径连续刚构桥成桥后的下挠情况,得出收缩徐变是导致连续刚构桥后期下挠的主要原因,而混凝土初始加载龄期是收缩徐变的主要影响因素.因此以某连续刚构桥为依托,采用按龄期调整的有效模量法考虑混凝土收缩徐变的影响,通过有限元软件模拟混凝土的收缩徐变对桥梁结构挠度的影响.结果表明,混凝土的加载龄期对连续刚构桥成桥后的挠度变形具有一定的影响,在施工过程中不能为了加快施工进度而盲目缩短混凝土的加载龄期,建议连续刚构桥混凝土的合理加载龄期取7 d左右为宜.

连续刚构桥; 收缩徐变; 有效模量法; 挠度变形; 合理加载龄期

目前陕西省共有153幅连续刚构桥,运营的连续刚构桥73座(129幅),在建连续刚构桥13座(24幅).陕北地区运营桥梁16座,其中14座是双幅桥,2座是单幅桥,共30幅;关中地区运营桥梁33座,其中25座是双幅桥,8座是单幅桥,共58幅;陕南地区运营桥梁24座,其中17座是双幅桥,7座是单幅桥,共41幅.13座在建桥梁中11座是双幅桥,2座是单幅,共24幅.

对各地区连续刚构桥跨中挠度的数据资料进行统计,结果见表1.

表1 连续刚构桥中跨跨中预拱值Table 1 The camber of maximum span of continuous rigid frame bridge at middle span cm

从表1中数据可以看出,随着运营时间的增长,连续刚构桥的跨中挠度不断增大.混凝土的收缩徐变使得结构产生一定的形变,且与运营年限有密切关系.混凝土收缩徐变是造成大跨度预应力混凝土连续刚构桥跨中下挠的主要原因,而混凝土初始加载龄期是收缩徐变的主要影响因素,因此对混凝土初始加载龄期的研究就显得尤为重要[1-2].国内外对混凝土初始加载龄期已经开展了较为系统的研究[3-8],文献[5]给出了按龄期调整的有效弹性模量法公式,并提出了相应的逐步计算的方法来模拟分析悬臂桥梁的施工;文献[6]通过有限元软件模拟不同方案的施工过程,结果表明,混凝土的收缩徐变与混凝土加载龄期有关,混凝土徐变随加载龄期的增长而单调的衰减;文献[7]从徐变模型出发,比较了不同加载龄期对长期下挠的影响,计算结果表明,大跨连续刚构桥长期下挠与混凝土加载龄期有关;文献[8]分析了长期载荷作用下混凝土徐变对连续刚构桥变形的影响规律,并对混凝土加载龄期、成桥交通开放时间等参数进行了探讨,分析结果表明,混凝土徐变对桥梁结构变形的影响是一个长期、逐渐累加的过程.目前针对混凝土的徐变机理,在工程界存在不同的理论和假设[9-11],文献[5-8]在分析过程中也没有采用统一的分析模型,同时也尚无可被普遍接受的理论模型.本文通过总结大量国内外文献的不同分析理论和假设,采用按龄期调整的有效模量法来考虑混凝土收缩徐变的影响[12],最后得出连续刚构桥施工过程中的合理加载龄期.

1 按龄期调整的有效弹性模量法

采用ACI-209(1992)推荐的混凝土徐变系数φ(t,τ)的表达式[13]

式中,t为长期载荷持荷时间;τ为加载龄期;φ∞为徐变系数终值.

由式(1)可知,混凝土的徐变与混凝土的加载龄期相关.利用按龄期调整得到的有效模量Eφ(i,i-1)代替混凝土的弹性模量Ec,替换后,在第i个时间间隔内由收缩、徐变产生的内力或应力增量与应变之间就会呈现线性关系.对于某个单元来说,在第i个时间间隔内,由混凝土的收缩、徐变产生的节点力增量为[5]

(2)

式中:ΔNe(i,i-1)、ΔMe(i,i-1)和ΔVe(i,i-1)分别为第i个时间间隔内的轴力增量、弯矩增量和剪力增量;ηij为混凝土松弛比;Ne(j)和Me(j)分别是第j个时间点上的轴力和弯矩;Eφ(i,i-1)为按龄期调整得到的有效模量;Δεsh,e(i.i-1)和ΔΨsh,e(i,i-1)分别为应变增量和曲率增量;Ac和Ic分别为混凝土构件截面面积和截面惯性矩;a和b是单元e的两个节点;ΔMa(i,i-1)和ΔMb(i,i-1)分别为节点a和节点b对应的惯性矩;l为构件单元长度.

当只考虑混凝土徐变影响时,就可以把式(2)、式(3)中的Eφ(i,i-1)AcΔεsh,e(i,i-1)和Eφ(i,i-1)IcΔΨsh,e(i,i-1)去掉,使计算得到简化.j=1,2,…,i-1是考虑前i-1个时段的影响.根据以上各式,同时考虑单元两端节点力及位移增量的区别,按单元规定的坐标系生成单元徐变、收缩载荷列阵为

按上述方法可以求出已完成结构全部单元在第i时间间隔内由混凝土收缩徐变产生的节点力增量和节点位移增量.把上述增量分别加到该时间间隔开始时有关节点力和节点位移上,就是该时间间隔终了时各单元的节点力与节点位移状态.利用按龄期调整得到的有效模量Eφ(i,i-1)代替混凝土的弹性模量Ec就能把徐变导致的应力增量引起的应变等效成弹性应变一样来计算,从桥梁施工开始到任一时间间隔的开始或终了时结构各个节点的力和位移状态都可逐一求得.根据连续刚构桥悬臂分块段施工的特点,通过专业桥梁有限元分析软件Midas Civil和桥梁博士对连续刚构桥按照悬臂施工过程进行仿真模拟分析.

2 工程背景及有限元模型概况

2.1 工程背景

以某高速公路上一连续刚构桥为例,该连续刚构桥主桥上部为2×(62.5+4×115+62.5) m预应力混凝土连续刚构,三向预应力体系,上部结构为C55混凝土.桥梁平面位于直线上,纵面位于0.63%的上坡(起点附近位于凹型竖曲线上),桥宽12.0 m.箱梁采用单箱单室截面,顶板宽12.0 m,底板宽6.5 m,翼缘板悬臂长为2.75 m.箱梁根部梁高6.5 m,高跨比为1/17.7;跨中梁高2.8 m,高跨比为1/41.1;根部底板厚0.9 m,跨中底板厚0.32 m;梁高及底板厚度均按二次抛物线变化.箱梁0号块顶板厚0.50 m,其余梁段厚0.28 m;0号块腹板厚1.0 m,其余梁段腹板8号梁段及以前为0.60 m,11号梁段及以后为0.45 m,9～10号梁段由0.60 m按直线变化至0.45 m.

2.2 有限元模型概况

为了验证本文计算理论的正确性,通过有限元软件Midas Civil和桥梁博士按连续刚构桥悬臂施工的特点,分阶段分别对该工程实例建立有限元分析模型.采用单元为梁单元,该桥共建立355个单元,201个节点,共划分为18个施工阶段.合龙顺序为先合龙中跨,然后合龙次中跨,最后进行边跨合龙.有限元模型见图1.

图1 有限元模型Fig.1 Finite element model

3 有限元分析及计算结果

考虑混凝土加载龄期为3、5、7、14 d四种工况,在恒载荷及钢束预加力作用下分析混凝土初始加载时龄期取值不同对各跨跨中挠度的影响,由于该连续刚构桥为双幅对称结构,故只分析边跨和中跨.

因为预应力混凝土受弯构件由于预加应力的作用在桥梁成桥后都会产生一定的上拱值, 为了便于对比分析,将桥梁的每跨的跨中挠度数据都以成桥时为0 cm开始计算, 每年的跨中挠度变化值取计算值与成桥预拱值之差. Midas Civil和“桥梁博士”具体的分析计算结果分别见表2和表3.

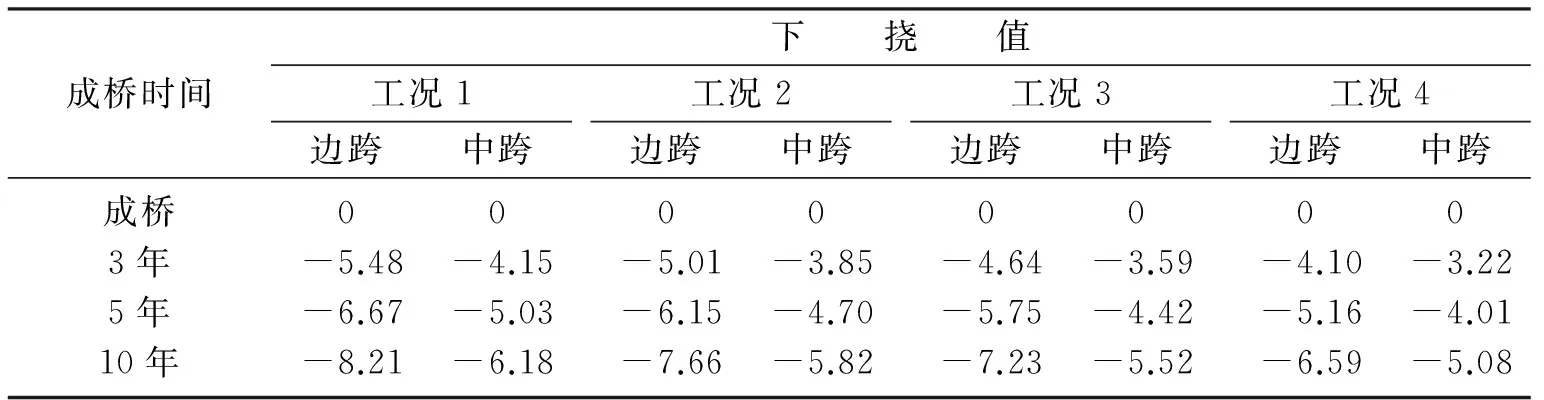
表2 Midas Civil软件计算的跨中下挠结果Table 2 The deflection value of mid-span calculated by Midas Civil software cm

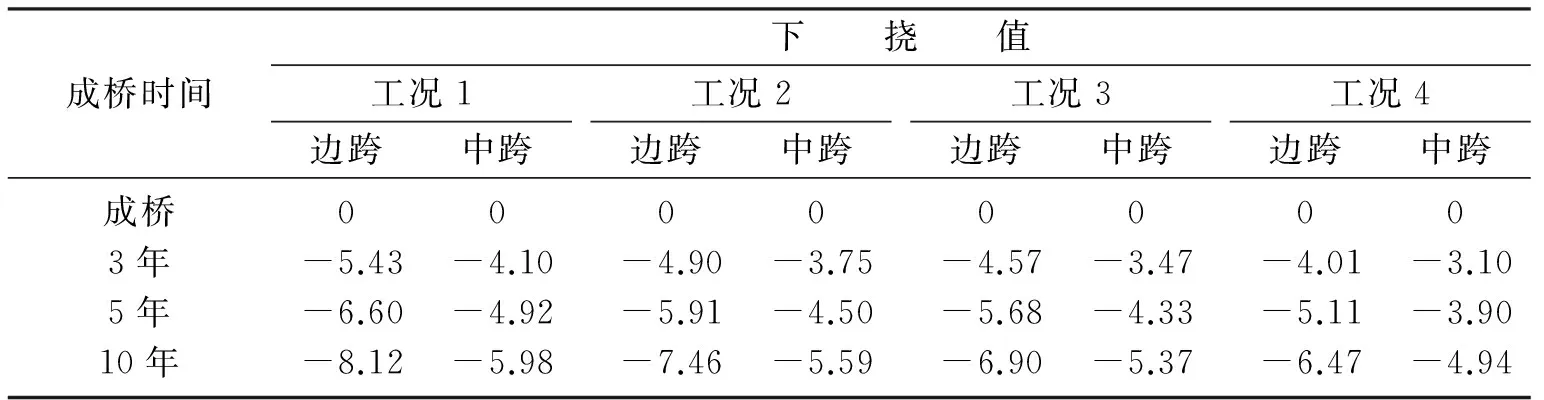
表3 桥梁博士软件计算的跨中下挠结果Table 3 The deflection value of mid-span calculated by Dr. Bridge software cm

从表2和表3中可以看出,成桥10年内跨中的挠度在逐渐增大,而边跨的下挠更为显著,最大下挠超过了8 cm,在工况2～工况4中也可以发现同样的规律.表明在成桥运营状态下混凝土的收缩徐变仍然在缓慢发生,桥梁结构的变形随着时间不断的增长.对比工况1～工况4作用下桥梁结构的跨中下挠值可以发现,混凝土初始加载龄期为3 d时,连续刚构桥成桥后,随着时间推移各跨跨中下挠值最大;加载龄期为14 d时,连续刚构桥成桥后,随着时间推移各跨跨中挠值最小;加载龄期为5～7 d时,连续刚构桥成桥后下挠值在上述两者之间.由此可见,随着加载龄期时间的延长,连续刚构桥成桥后跨中下挠的现象得到减缓.但是在连续刚构桥梁的实际施工过程中,混凝土的初始加载龄期不可能无限延长,所以就需要确定一个比较合理的加载龄期来适当的控制连续刚构桥梁在成桥后期跨中下挠的现象.

对Midas Civil和“桥梁博士”两种软件分析计算得出的结果进行对比,两种软件的误差分析如表4所示.

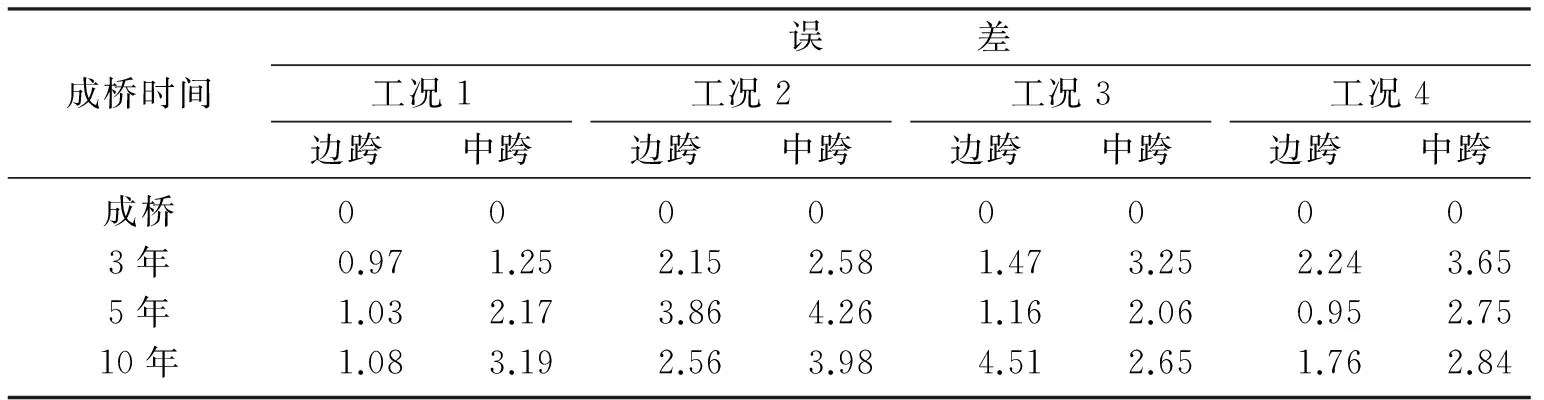
表4 两种软件计算结果的误差对比Table 4 Calculation error between two different software %

注: 误差=1-Midas Civil分析计算结果/Dr. Bridge分析计算结果.

从表4计算结果的误差分析可以表明Midas Civil和“桥梁博士”这两个软件分析计算得到的结果差异不大,最大误差均不超过5%,由此可见软件分析计算是正确的,同时表2和表3在不同工况下的下挠值也和表1的统计结果比较接近,这也证明了本文分析思路和分析方法的正确性.

4 结 论

徐变收缩对混凝土桥梁具有长期的影响,并且与桥梁结构形式、材料特性以及施工方法等因素有关.本文分析了影响混凝土收缩徐变的因素并确定混凝土初始加载龄期是主要影响因素之一,以某连续刚构桥为例,分析加载龄期的变化对多跨连续刚构桥长期挠度的影响.通过对比分析加载龄期分别为3、5、7、14 d时连续刚构桥成桥后结构的挠度变化,发现适当地延长混凝土的加载龄期能够有效缓解连续刚构桥的后期挠度的增大.因此,在施工过程中不能为了加快施工进度盲目缩短混凝土的加载龄期. 建议应当适当延长连续刚构桥混凝土的初始加载龄期,取7 d左右为宜.

[ 1 ] 张汉一,周凌宇,贺桂超,等. 徐变对大跨度预应力混凝土连续箱梁桥施工线形控制的影响[J]. 铁道科学与工程学报, 2012,9(5):13-18. (ZHANG H Y,ZHOU L Y,HE G C,et al. The effect of creep on the construction of linear control of large-span pre-stressed concrete continuous box beam bridge[J]. Journal of Railway Science and Engineering, 2012,9(5):13-18.)

[ 2 ] 熊维. 不同强度早龄期混凝土徐变及徐变对长期载荷作用下预应力构件的影响[D]. 天津: 天津大学, 2011. (XIONG W. Different early-age strength of concrete-creep and creep under load for long-term effects of pre-stressed beam master degree thesis[M]. Tianjin: Tianjin University, 2011.)

[ 3 ] KOVLER K. Drying creep of concrete in terms of the age-adjusted effective modulus method[J]. Magazine of Concrete Research, 1997,49(181):345-351.

[ 4 ] SCHEINER S,HELLMICH C,ASCE A M. Continuum microviscoelasticity model for aging basic creep of early-age concrete[J]. Journal of Engineering Mechanics, 2009,135:307-323.

[ 5 ] 傅木森,曹玉玲. 按龄期调整的有效模量法计算混凝土的收缩徐变效应[J]. 国防交通工程与技术, 2004,2(4):20-22. (FU M S,CAO Y L. The calculation for concrete creep simulation of the PC bridge construction process with age-adjusted effective modulus method[J]. Traffic Engineering and Technology for National Defence, 2004,2(4):20-22.)

[ 6 ] 方淑君,肖啸,李杰. 多跨连续梁合龙顺序的优化以及混凝土初始加载龄期的探讨[J]. 铁道科学与工程学报, 2013,10(4):24-29. (FANG S J,XIAO X,LI J. Optimization of sequences of multi-span continuous beams’ closure and discussion of initial loading age of concrete[J]. Journal of Railway Science and Engineering, 2013,10(4):24-29.)

[ 7 ] 杨西福. 混凝土徐变对大跨连续刚构桥长期下挠的影响分析[J]. 中外公路, 2010,30(5): 183-185. (YANG X F. The effect of concrete creep on long term deflection of long span continuous rigid frame bridge[J]. Journal of China and Foreign Highway, 2010,30(5):183-185.)

[ 8 ] 王建章,章金桥,王静. 长期载荷作用下混凝土徐变对连续刚构桥变形的影响分析[J]. 交通科技, 2014(5):7-9. (WANG J Z,ZHANG J Q,WANG J. Influence analysis of concrete creep on deformations of continuous rigid frame bridge under long term load[J]. Transportation Science and Technology, 2014(5):7-9.)

[ 9 ] 胡狄,陈政清. 从短期试验结果预测新建预应力混凝土梁收缩和徐变的长期效应[J]. 中国铁道科学, 2003,24(3):44-49. (HU D,CHEN Z Q. Prediction of long-term effect of creep and shrinkage on newly-built prestressed concrete bridge based on short-term test results[J]. China Railway Science, 2003,24(3):44-49.)

[10] 洪帆,周征征. 混凝土收缩徐变在连续刚构桥施工中的影响分析[J]. 交通科技, 2009(Z1):1-3. (HONG F,ZHOU Z Z. The analysis of the influence of the concrete creep and shrinkage on continual rigid frame bridge during the construction[J]. Transportation Science and Technology, 2009(Z1):1-3.)

[11] 王瑞花. 湘江大跨度预应力连续梁桥的仿真计算和收缩徐变研究[D]. 北京: 北京交通大学, 2008. (WANG R H. The artificial calculation and creep and shrinkage analyze of the long-span PC continuous beam bridge in Xiangjiang[D]. Beijing: Beijing Jiaotong University, 2008.)

[12] 周履,陈永春. 收缩、徐变[M]. 北京: 中国铁道出版社, 1994. (ZHOU L,CHENG Y C. Creep and shrinkage[M]. Beijing: China Railway Press, 1994.)

[13] ACI Committee 209. Prediction of creep, shrinkage, and temperature effects in concrete structures[R]. American Concrete Institute, 1992.

【责任编辑: 赵 炬】

Rational Loading Age of Long-Span Continuous Rigid Frame Bridge

HuangXuqin,LiYilin,AnPinghe,ZhengPeng

(Key Laboratory for Bridge and Tunnel of Shaanxi Province, Chang’an University, Xi’an 710064, China)

The influence of concrete shrinkage and creep on the mechanical performance of long-span continuous rigid frame bridge in the service phase is analyzed, based on the statistics data of the existing continuous rigid frame bridge in Shaanxi province. The results show that loading age is a main influence factor of concrete creep and shrinkage. Taking a continuous rigid frame bridge as an example and using the age-adjusted effective modulus to consider the concrete shrinkage and creep effects. The deflection of bridge caused by concrete shrinkage and creep is studied by the finite element software. The results indicate that the initial loading age of concrete has a certain influence on the deflection of the continuous rigid frame bridge. Therefore, it can not speed up the construction progress blindly and shorten the loading age of concrete. It is suggested that the initial loading age of the concrete of the continuous rigid frame bridge should be prolonged appropriately, and the recommended concrete loading age is about 7 days.

continuous rigid frame bridge; creep and shrinkage; effective modulus; deflection transformation; rational loading age

2016-11-29

陕西省交通运输厅科技资助项目(13-25k).

黄叙钦(1992-),男,广西贵港人,长安大学硕士研究生.

2095-5456(2017)03-0233-06

U 448.23

A