潮河大桥基准索股架设计算与控制
曹 竞(河南省交通规划设计研究院股份有限公司, 河南 郑州 450002)
潮河大桥基准索股架设计算与控制
曹 竞
(河南省交通规划设计研究院股份有限公司, 河南 郑州 450002)
以潮河大桥多塔地锚式悬索桥为例,着重介绍基准索股控制和索股线形的计算方法.阐述了温度对控制点垂度的影响和基准索股架设调整方案.结果表明,基准索股架设控制效果良好,可为类似工程提供借鉴参考.
悬索桥; 基准索股; 施工控制; 温度
悬索桥作为一种桥型优美的桥梁,以其结构造型美观、经济性能较好、对地形和地质状况适应性强等优点越来越受到工程界的青睐[1-3].然而,通过目前掌握的资料来看,国内外建成的多塔悬索桥尚不多见,国外已有的多塔连跨悬索桥工程实例还仅限于中小跨度(最大跨度210 m),国内已建成的多塔悬索桥有3~4座,最大跨径可达上千米[4].
1951年法国建成三塔四跨悬索桥Chatillon桥,桥跨布置为(92+2×76+92)m,桥塔为圬工结构.1961年日本建成的第1座三塔四跨悬索桥是小鸣门桥,桥跨布置为(70.6+2×160+50.8)m,桥宽7 m,中塔为钢筋混凝土塔,主缆在中塔处断开并锚固于中塔.2007年泰州长江公路大桥正式开工建设,主桥采用三塔两跨悬索桥,由桥墩来支承两边跨,桥跨布置为(390+2×1 080+390)m,桥塔为纵向呈人字形的全钢中塔,加劲梁选用3.5 m高钢箱梁,主缆矢跨比为1/9[5].2008年开始建设的马鞍山大桥的左汊主桥采用三塔两跨悬索桥,由桥墩来支承两边跨,桥跨布置为(360+2×1 080+360)m.中塔采用I字形钢混结合塔,采用塔梁固结体系,加劲梁为扁平流线型钢箱梁,主缆矢跨比为1/9[6].2010—2014年建设的鹦鹉洲长江大桥主桥采用跨径(225+2×850+225)m三塔四跨钢板结合梁悬索桥.
1 工程简介
郑州市国家经济开发区经南八路潮河大桥是一座三塔四跨地锚式悬索桥,孔径布置为(64+136+136+64)m,全长400 m.主跨主缆理论跨径136 m,理论垂度为27.2 m,理论垂跨比为1∶5;边跨主缆理论垂度为6.319 m,理论跨度为66.5 m,理论垂跨比为1∶10.52.主塔为鱼腹式预应力混凝土结构,主梁采用钢箱梁,在边、中塔下横梁处设隔震支座,限制钢箱梁三向线位移.主缆经中塔、边塔塔顶鞍座、边墩顶散索鞍座转向后锚固在混凝土锚碇内,锚碇结构与桥台基础合二为一进行整体设计.桥面总宽度为45 m,组成为6 m(慢行交通)+5 m(吊索区)+23 m(机动车)+5 m(吊索区)+6 m(慢行交通)(如图1所示).
全桥共两根主缆,采用预制平行索股法架设(PPWS),每根主缆含19股平行钢丝索股,每股含127根φ5 mm的镀锌高强钢丝,每根主缆共2 413丝,竖向排列成尖顶的正六边形.钢丝抗拉强度1.670 GPa,紧缆后主缆为圆形,直径为271.2 mm(索夹处)和274.6 mm(索夹间).
2 施工控制参数的确定
由于悬索桥独特的结构形式和受力特点,主缆的架设施工成为悬索桥施工控制的重点和难点[7].主缆的线形控制包括两个步骤:基准索股的架设控制和其他一般索股的线形控制.架设基准索股之后,即可以按照若即若离原则安装其他索股,因此基准索股的施工控制是整个主缆线形控制的关键.悬索桥施工控制计算和测量的难度及工作量都比常规桥型大,在基准索股架设之前,有两方面的工作必须要做[8]:一是基准索股线形和控制点坐标计算;二是施工参数的收集.不同的计算方法会造成控制方法和结果的不同,而控制参数是否精确又决定了施工控制的精确度.

图1 潮河大桥桥型布置图Fig.1 Bridge layout and arrangement diagram of Chaohe Bridge
主缆安装之前主塔、锚碇等已经就位,主索鞍与散索鞍安装时要考虑建成桥塔的偏位与压缩,尽量消除前期施工误差的影响,控制方法是调整主索鞍和散索鞍的IP点.主缆IP点[9]是一个虚拟点,表示不同跨主缆中心线在主索鞍和散索鞍转折处的交点,也是主缆索股与索鞍的理论交点.主缆在IP点受主塔通过索鞍传递的支撑力,相邻IP点之间的主缆索股在空缆时呈悬链线分布,成桥为分段悬链线形.根据实测鞍座坐标、高程调整安装,使索鞍IP点与设计IP点尽量重合,可以最大限度地消除施工误差.索鞍安装之后,再次精确测量索鞍的安装位置,推算实际IP点三维坐标,计算施工误差,根据误差调整计算模型中主缆的边界条件,得出新的控制点坐标.
设计计算时一般将模型置于基准温度下.在实际施工时,索股线形容易受温度与日照的影响发生变化[10].另外,影响索股线形的是主塔索鞍IP点坐标,此点依附于桥塔,而混凝土桥塔也会受温度和日照影响发生偏位,收缩徐变也会引起塔顶高程变化,所有这些实际与计算模型的差异都会造成控制点坐标的变化,在基准索股架设时一定要考虑进去.
3 索股线形计算方法
基准索股线形计算的基本原则是无应力长度不变.即索股在两点之间的无应力长度确定后,无论在何种状态下其无应力长度均为定值.依据此原则可以分析主缆在温度、载荷等作用下的内力及变形[11].现代悬索桥一般使用高强镀锌钢丝制作主缆,对于大跨度悬索桥,认为跨度范围内主缆抗弯刚度极小,计算时作为柔性索,并有以下假定[12].
(1) 索为理想柔性,不承担弯矩,只考虑拉力;
(2) 主缆材料完全符合胡克定律,不考虑材料的非线性;
(3) 主缆索股在受力过程中截面性质不发生变化.
图2为同时承受横向与纵向均布载荷的一根悬索,由于假定索为理想柔性,拉力T方向与索相切,列出静力平衡条件.
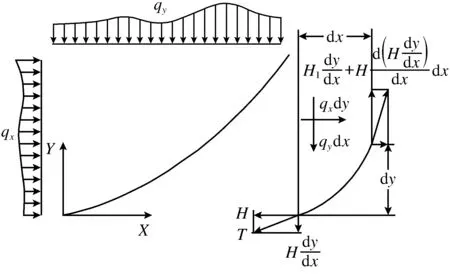
图2 均布载荷作用下悬索微段单元
一般只考虑竖向载荷,即认为qx=0,根据式(1)推出张力T的水平分力H为定值,式(2)写成:
若q沿任意的曲线S分布,则有:
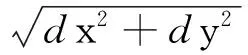
将式(4)代入式(1),得:
对竖向载荷进行不同简化,所得的线形也不同.若q=0,则索曲线退化为直线;若q沿跨度均布,则索股成为抛物线;若q曲线与索曲线重合,则载荷沿索形分布,索曲线成为悬链线.一般而言,悬链线状态最接近悬索实际载荷状态.但是对于小跨径悬索桥而言,抛物线法与分段悬链线计算结果十分相近,可以满足施工控制精度需要.本桥使用传统抛物线理论进行基准索股线形计算.
抛物线理论认为主缆自重与其他恒载相比影响很小.因此,可将恒载简化为沿跨度均布,不考虑主缆增长对载荷曲线的影响.
如图3所示,将成桥状态下载荷换算为计算均布载荷q,f为跨中垂度,C为两相邻塔的高差,L为计算跨径,T为主缆索力,H为主缆索力水平分力.支点处的边界条件
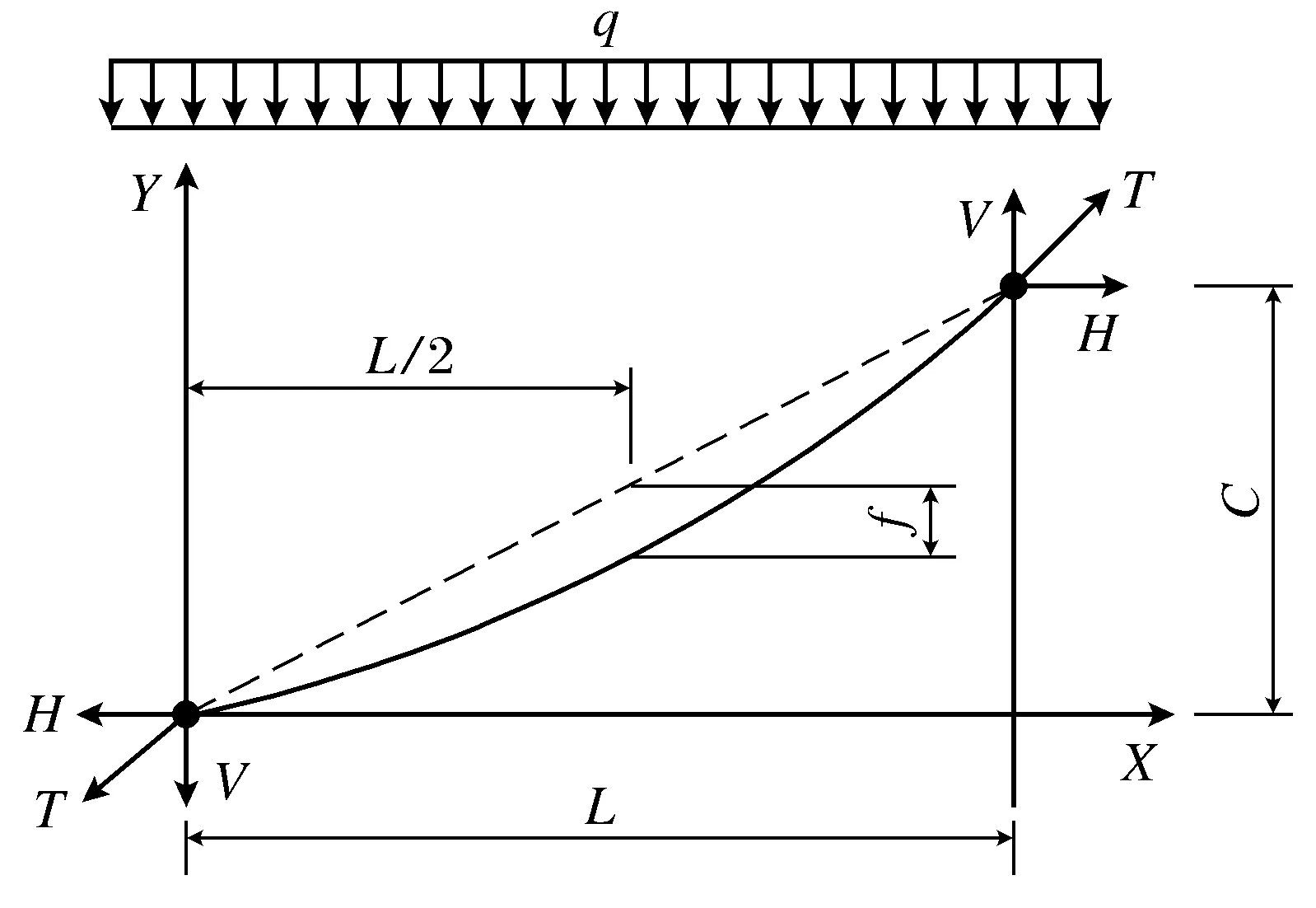
图3 抛物线计算理论图Fig.3 Diagram of parabola theory
抛物线曲线方程为
主缆索长
(8)
S=
(9)
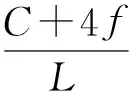
抛物线主缆伸长量
主缆无应力长度
有了索股曲线方程就可以计算出基准索股无应力索长、内力、伸长量和任一点的坐标.
4 基准索股控制计算方法[13-15]
索股线形发生变化时各跨跨中点的坐标与高程都会发生变化.一般在工程上用两种方式确定控制点.第一种方法是选取索股跨中处的某固定点,为便于计算,一般是主缆中点,在此点做好标记,每次测量时都将棱镜放在这一固定位置,测量该点的里程与高程,并且通过有限元计算得出每次调整时坐标变化情况,将实际里程、高程调整到计算目标值即可.第二种方法是固定索股跨中里程位置,每次通过全站仪放样确定此点位置,然后测量此点高程,结合计算结果调整索股,将此点高程调整到计算目标值.两种方法均能实现高精度施工控制,且各有优点,第一种方法不用每次放样,可以快速确定目标点,缺点在于需要每次变化后的里程和高程计算结果,每次控制两个因素;第二种方法只需要控制固定里程处的高程,计算工作量稍小,缺点在于每次调整索股线形后都需要重新放样才能确定目标点位置,而且后期测量时也需要放样.实际上控制点是不停在变化的,本桥采用第二种控制方法.
基准索股线形调节一般是先中跨、再边跨,测量时采用绝对垂度测量,固定跨中点里程后,通过调节主索鞍处索长来调节跨中高程.控制点高程值主要受温度与索长变化影响,计算出温度变化对控制点高程影响,即可得到不同温度下的高程值;计算出索长变化对控制点高程影响,即可得到高程调节方法.实际计算时也要考虑温度影响下主塔变位造成的跨度变化对控制点高程的影响.
4.1 基准索股垂度受跨度误差的影响
按载荷沿弦长分布、索股线形满足式(7),将式(9)中f看做是L的函数进行微分,得到垂度与跨度关系如下:
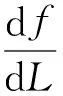
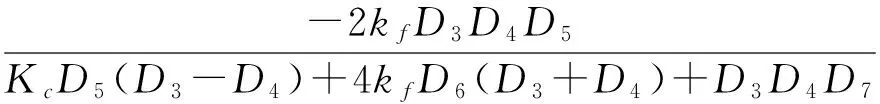
(12)
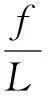
得出潮河大桥边、中跨垂度随跨度变化关系:
4.2 基准索股垂度受索长误差的影响
将式(9)中f看做S的函数进行微分,得到垂度与索长关系
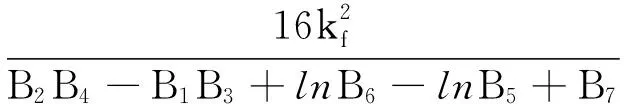
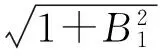
经计算,索股跨中垂度调整量与索长变化量的关系如下.
中跨Δf=1.097ΔS,即中跨索长增加1 cm,跨中垂度降低1.097 cm;索长减少1 cm,跨中垂度抬高1.097 cm.
边跨Δf=2.668ΔS,即边跨索长增加1 cm,跨中垂度降低2.668 cm;索长减少1 cm,跨中垂度抬高2.668 cm.
4.3 基准索股垂度受温度误差的影响
潮河大桥设计计算基准温度为15 ℃,但在实际施工时,基准索股架设的环境温度与基准温度有差异,架设基准索股前必须考虑温度误差影响.主缆垂度与温度变化关系式可由索长变化量与温度关系式ΔS=α·ΔT·S直接导出.
不同施工温度下,基准索股控制点高程不同.经计算,高程变化值Δh(m)与温度变化值ΔT(℃)关系如下:
中跨Δh=-0.001 954 6ΔT;
边跨Δh=-0.002 766 4ΔT.
ΔT为架设基准索股时缆索实测温度与设计基准温度的差值.
5 潮河大桥基准索股架设控制
5.1 基准索股线形调整方案
在施工步道架设前,主塔处于自由状态下,需要进行全天候观测,取得温度变化、光照角度与主塔变位资料,尽可能在温度变化不大且无日照的阴天作竣工测量,精密做出墩中心十字线和鞍座十字线.基准束安装后,精密测量中跨、边跨的跨距资料,并记录测量时的温度,根据这些资料计算基准索股的空载线形.调整时间,选择在温度影响较少的夜间进行,温度稳定条件为长度方向索股温差小于2 ℃,横向索股温差小于1 ℃.跟踪测量气温变化、束温变化、挠度变化情况,分析判定基准索股的线形与设计线形是否一致,若有出入,应于下一工作夜间继续观测调整.
调整顺序为先中跨、后边跨,调整好的索股不得在鞍槽内滑移.索力的调整以设计提供的数据为依据,其调整量应根据调整装置中测力计的读数和锚头移动量双控确定.其精度要求为实际拉力与设计值之间的允许误差为设计锚固力的3%.
基准索股标高必须连续3 d在夜间温度稳定时进行测量,三次测出结果误差在容许范围内时,取三次的平均值作为该基准索股的高程.高程稳定后方可认为调整完成.
本桥垂度调整控制标准即基准索股高程允许误差如下:中跨跨中6.8 mm,边跨跨中13.6 mm,上下游基准索股高差10 mm.
5.2 架设过程温度控制
在主缆生产时,要求生产单位同时制作2 m长的主缆索股节段作为测温索,与主缆一同运至现场,用以观测现场主缆温度变化.根据温度观测记录,晚21∶30~凌晨01∶30期间最高温度与最低温度不超过1 ℃,温度变化比较均匀,是进行索股调整的最佳时段.
按照方案,夜间进行基准索股调整,将控制点调至设计高程.开始架设主缆基准索股后,连续3 d进行基准索股高程观测,高程控制点标记在索股上表面,基准索股的温度根据测温索的无线测温系统监测数据、大气温度及主缆表面温度综合选取,观测结果如下表1~表3所示.可以看出,经3 d连续观测,基准索股高程变化均在允许误差范围内,基准索股线形控制效果良好.

表1 第1 d基准索股控制点观测结果(观测温度:3℃)Table 1 Control points observation results of datum strand on the first day(Temperature: 3 ℃) m

表2 第2 d基准索股控制点观测结果(观测温度:4 ℃)Table 2 Control points observation results of datum strand on the second day(Temperature: 4 ℃) m

表3 第3 d基准索股控制点观测结果(观测温度:4 ℃)Table 3 Control points observation results of datum strand on the third day(Temperature: 4 ℃) m
6 结 语
(1) 潮河大桥为中小跨径悬索桥,采用抛物线理论进行基准索股线形理论计算,考虑了跨度误差、索长误差和温度等因素影响,完全可以满足施工控制精度的需要.
(2) 潮河大桥基准索股架设线形调整采用放样索股跨中里程位置,测量该点高程到计算目标值.实测数据表明,基准索股高程变化处于规范允许误差范围内,基准索股架设控制效果良好.
(3) 本工程采用的基准索股线形调整方法原理简明、实用性强,适合中小跨度悬索桥,值得类似工程借鉴参考.
[ 1 ] 邵旭东,胡建华. 桥梁设计百问[M]. 2版. 北京:人民交通出版社, 2005:213-216. (SHAO X D,HU J H. Bridge design: question &answers[M]. 2nd ed. Beijing: China Communications Press, 2005:213-216.)
[ 2 ] GIMSING N J. Cable supported bridges: concept &design[M]. Beijing: China Communications Press, 2002:178-180,183-185.
[ 3 ] YOSHIDAO O,OKUDA M,MORIYA T. Structural characteristics and applicability of four-span suspension bridge[J]. Journal of Bridge Engineering, 2004,9(5):453-463.
[ 4 ] 张劲泉,曲兆乐,宋建永,等. 多塔连跨悬索桥综述[J]. 公路交通科技, 2011,28(9):30-45. (ZHANG J Q,QÜ Z L,SONG J Y,et al. Overview of multi-pylon multi-span suspension bridge[J]. Journal of Highway and Transportation Research and Development, 2011,28(9):30-45.)
[ 5 ] 杨进,徐恭义,韩大章,等. 泰州长江公路大桥三塔两跨悬索桥总体设计与结构选型[J]. 桥梁建设, 2008(1):37-40. (YANG J,XU G Y,HAN D Z,et al. Over design and structural type selection of three-tower and two-span suspension bridge of Taizhou Changjiang River Highway Bridge[J]. Bridge Construction, 2008(1):37-40.)
[ 6 ] 杨光武,徐宏光,张强. 马鞍山长江大桥三塔悬索桥关键技术研究[J]. 桥梁建设, 2010(5):7-11. (YANG G W,XU H G,ZHANG Q. Study of key techniques for three-tower suspension bridge of Maanshan Changjiang River Bridge[J]. Bridge Construction, 2010(5):7-11.)
[ 7 ] 薛光雄,沈锐利,先正权,等. 悬索桥基准丝股线形的确定与测控[J]. 桥梁建设, 2004(4):4-6. (XUE G X,SHEN R L,XIAN Z Q,et al. Determination measurement and control of datum wire strand geometry of suspension bridge[J]. Bridge Construction, 2004(4):4-6.)
[ 8 ] 陈炜,刘海忠,石建华,等. 福州鼓山大桥关键技术研究[J]. 桥梁建设, 2010(5):16-19. (CHEN W,LIU H Z,SHI J H,et al. Study of key techniques for Gushan Bridge in Fuzhou[J]. Bridge Construction, 2010(5):16-19.)
[ 9 ] 张哲. 混凝土自锚式悬索桥[M]. 北京:人民交通出版社, 2005. (ZHANG Z. Concrete self-anchored suspension bridge[M]. Beijing: China Communications Press, 2005.)
[10] 郭福,乔卫华. 温度对悬索桥基准索股架设的影响[J]. 现代交通技术, 2009(2):55-57. (GUO F,QIAO W H. Influence of temperature on the datum strand erection of suspension bridge[J]. Modern Transportation Technology, 2009(2):55-57.)
[11] 唐茂林. 大跨度悬索桥空间几何非线性分析与软件开发[D]. 成都:西南交通大学, 2003. (TANG M L. Spatial geometric nonlinear analysis and software development of long span suspension bridge[D]. Chengdu: Southwest Jiaotong University, 2003.)
[12] 谭红梅,袁帅华,肖汝诚. 大跨度悬索桥的基准索股调整[J]. 中国铁道科学, 2010,31(1):38-43. (TAN H M,YUAN S H,XIAO R C. Datum strand adjustment of long span suspension bridge[J]. China Railway Science, 2010,31(1):38-43.)
[13] 钟继卫,高建学,王戒躁. 大跨度悬索桥基准索股施工控制[J]. 世界桥梁, 2006(2):41-43. (ZHONG J W,GAO J X,WANG J Z. Construction control of datum strand of long span suspension bridge[J]. World Bridges, 2006(2):41-43.)
[14] 吕哲,郑力. 确定自锚式悬索桥索力的影响矩阵法[J]. 沈阳大学学报(自然科学版), 2014,26(5):404-407. (LYU Z,ZHENG L. Determine cable force of self-anchored suspension bridge by influence matrix method[J]. Journal of Shenyang University(Natural Science), 2014,26(5):404-407.)
[15] 郭雪妍,王超,张恒心,等. 潮河大桥悬索桥猫道设计与计算分析[J]. 沈阳大学学报(自然科学版), 2017,29(1):66-70. (GUO X Y,WANG C,ZHANG H X,et al. Design and calculation analysis of catwalk of Chaohe River Suspension Bridge[J]. Journal of Shenyang University(Natural Science), 2017,29(1):66-70.)
【责任编辑: 赵 炬】
Calculation and Control of Datum Strand Erection of Chaohe Bridge
CaoJing
(Henan Provincial Communications Planning Survey & Design Institute Co. Ltd., Zhengzhou 450002, China)
Taking the self-anchored suspension bridge of Chaohe Bridge as an example, the calculation method of datum strand control and cable strands are mainly introduced.The temperature influence on strand sag at control points and datum strand erection adjustment scheme is expounded. The results show that the control effect of the datum strand erection is good, which can provide reference for similar projects.
suspension bridge; datum strand; construction control; temperature
2016-07-23
曹 竞(1983-),男,河南永城人,河南省交通规划设计研究院股份有限公司工程师.
2095-5456(2017)03-0238-06
U 442
A
——垂度法

