多状态系统的动态可靠性度量及重要度分析*

邱光琦 黄思† 古莹奎

(1．华南理工大学 机械与汽车工程学院, 广东 广州 510640;2.江西理工大学 机电工程学院, 江西 赣州 341000)

多状态系统的动态可靠性度量及重要度分析*

邱光琦1黄思1†古莹奎2

(1．华南理工大学 机械与汽车工程学院, 广东 广州 510640;2.江西理工大学 机电工程学院, 江西 赣州 341000)

为有效表征性能退化条件下多状态系统的可靠性,确定各组件(状态)对系统的影响,文中对性能状态进行分析,提出了新的动态可靠性度量指标和性能水平限制下的重要度计算方法.首先,针对多状态系统马尔可夫过程的组合爆炸问题,应用通用生成函数法求解系统(组件)各状态的概率和可靠度、性能状态期望值、性能状态平均期望值和性能状态驻留时间长度等4种动态可靠性度量指标.然后,为满足系统(组件)的不同性能需求,综合评估各组件(状态)对系统的影响,用性能期望值定义了给定性能水平下的Birnbaum重要度、Fussell-Vesely重要度、风险业绩值和风险降低值.四缸柴油机燃油供给系统的实例结果表明,文中方法既可准确地求解系统及其组件(油泵和喷油阀)的性能状态概率,以及性能退化条件下各性能状态的可靠度、期望值、平均期望值和驻留时间长度,又能根据性能水平限制下的4种重要度综合评估各性能状态及组件对系统的影响,有助于识别出系统最薄弱的环节,提高系统可靠性.

多状态系统;可靠性;马尔可夫过程;动态可靠性度量;性能水平约束;重要度

传统可靠性理论将系统假设为工作状态和完全失效状态,在此假设条件下涌现出了大量的可靠性评估方法,如故障树和贝叶斯方法等[1],并应用于核电站、宇航、机械和化工等领域.然而,深入研究工程实际问题后发现,传统可靠性理论表现出诸多局限性,如无法描述多失效模式和多性能系统[2].实际上，由于振动冲击、负载以及疲劳损伤等的作用,使得系统性能逐渐劣化,系统从正常工作到完全失效需要经历一系列中间过渡状态(即性能状态),这些中间状态既可能是连续的,如系统随着损伤累积而不断连续衰退,也可以是离散的,如系统从性能较高的状态跳转到性能较低的状态,并且各个状态的失效规律可能不尽相同,此时系统呈现出多状态特性,而多状态信息往往对揭示复杂系统失效机理、剩余使用寿命以及提高系统效率和经济性至关重要[3].

多状态系统的定义及可靠性概念在20世纪70年代首次被提出[4],随后几十年其可靠性理论不断完善和发展.现有多状态系统的可靠性建模方法主要有由二态系统布尔模型扩展而成的多值模型[5]、随机过程模型[6]、通用生成函数法[7]和Monte-Carlo仿真[8]等,文献[9]已对现有多状态系统可靠性建模方法进行了分析和总结.然而,由于外部环境和设备老化等因素的影响,系统(组件)性能往往处于动态变化的过程,现有多状态可靠性度量指标多数由传统可靠性度量指标扩展而来[10],未考虑系统性能退化的影响,均无法有效地描述和表征系统性能的退化程度.目前,人们已对多状态系统重要度做了大量的研究工作,如曾亮等[11]给出了其定义及计算公式,Li等[12]给出了多状态系统多值决策图的重要度计算方法.然而,系统在运行过程中受到各因素的影响而导致性能需求不同,因此研究性能水平限制下的重要度计算方法更贴近现实[13].

文中在已有研究[9,13- 16]基础上,充分考虑了系统性能的退化规律,结合通用生成函数法给出了能表征系统性能退化程度的动态可靠性度量指标,并探讨在不同性能水平划分下各组件(状态)的重要度,确定组件(状态)对系统的影响,识别出系统的最薄弱环节,以提高多状态系统的可靠性.

1 基于通用生成函数法的多状态系统 可靠性分析

多状态系统由多状态组件通过布尔逻辑关系组合而成,不同组件有不同的性能状态,而每个性能状态都对应一个性能水平值[13].假设系统由n个组件构成,第j(j∈{1,2,…,n})个组件有i(i∈{1,2,…,Kj})个性能状态(Kj为第j个组件的最佳性能状态,1为最差性能状态,从最佳性能状态到最差性能状态Kj→1,组件的性能水平逐渐下降);在t时刻,第j个组件的性能状态i的性能水平值为gji,则第j个组件的性能水平分布为Gj(t)={gj1,gj2,…,gjKj}.Ln={g11,g12,…,g1k1}×{g21,g22,…,g2k2}×…×{gn1,gn2,…,gnkn}为多状态系统所有可能的性能水平值集合,此时多状态系统性能状态集为{1,2,…,K},共有K个性能状态(K表示系统最佳性能状态,1表示最差性能状态,从性能状态K→1时系统性能水平逐渐下降),K个性能状态相应的性能水平值集为WK={g1,g2,…,gK}.注意系统及其组件性能状态必须大于等于2,即K≥2和Kj≥2.实际上,传统可靠性理论假设为工作和完全失效两种状态,是多状态系统的最简形式,即系统及其组件性能状态等于2的情况(K=2和Kj=2),它们之间的唯一区别在于结构函数:

(1)

目前多状态系统可靠性分析大多假定系统服从马尔可夫性质,然后根据布尔逻辑关系建立柯尔莫哥洛夫微分方程组,从而求解出各性能状态的可靠性度量指标.此方法计算繁琐且费时,并且由于系统及其组件结构复杂,系统及其组件之间往往存在交互、耦合等情况,随着组件数的增加,系统性能状态呈指数增加.如一个含有n个组件的系统,每个组件有n个性能状态,则系统将拥有nn个性能状态,存在状态空间组合爆炸问题[17].采用通用生成函数法在一定程度上可缓解状态空间组合爆炸问题,因此先根据马尔可夫过程理论建立柯尔莫哥洛夫微分方程组对组成系统的各组件进行可靠性分析,再根据组件布尔逻辑关系组合，利用通用生成函数法对系统可靠性进行分析,可有效地减轻计算复杂度[18].多状态系统结构为串联时,其输出性能水平等于最坏单元性能,其通用生成函数User为[7]

(2)

式中,pji(t)表示t≥0时第j个组件处于第i个性能状态的失效概率.

多状态系统结构为并联时,其输出性能水平有两种情况:协同型或竞争型.当为协同型时,输出性能水平具有相加性;当为竞争型时,输出性能水平为最坏单元性能.通用生成函数Upar为[7]

(3)

2 多状态系统的可靠性度量和重要度 分析

2.1 动态可靠性度量

多状态系统可靠性度量指标(如可靠度、失效概率、平均寿命和有效度等)未考虑到系统性能退化的影响,无法有效地描述和表征性能退化程度[10].文中考虑了劣化(衰退)或外部环境因素对系统的影响,认为系统及其组件的性能水平处于动态变化的过程,系统从最佳性能状态到完全失效状态需要经历K个性能状态,性能状态从K变到1时系统及其组件性能水平逐渐降低,可以从较高的性能状态退化到更低的相邻性能状态或更低的其他性能状态,正常情况下无法从较低性能状态迁移到较高的性能状态.为有效地表征系统及其组件性能退化情况下的可靠性,文中对性能退化情况下的性能状态做进一步分析,从概率角度定义,假定性能状态服从马尔可夫性质,从而给出不同性能状态需求下系统及其组件的可靠度、性能状态期望值、性能状态平均期望值、性能状态驻留时间长度等动态可靠性度量指标.可靠度表示系统在规定条件和规定时间内完成规定功能的概率,定义在不同性能状态i(i=1,2,…,K)下系统的可靠度为

(4)

式中,pi+1(t)为i+1性能状态的失效概率.

为表征系统及其组件的平均性能状态水平,定义性能状态期望为

(5)

为表征给定时间[0,t0]内系统及其组件性能状态的退化程度,定义瞬态性能状态平均期望值为

(6)

状态i累积驻留时间期望或者说平均寿命(MTTF)为

(7)

则性能状态i驻留时间长度为

(8)

2.2 性能水平α划分下的重要度

(9)

式中,ph(t)为性能状态h的失效概率,p≤α(t)为≤α的失效概率,p>α(t)为>α的失效概率.此时,系统(组件)的状态概率为p(t)=p≤α(t)+p>α(t).

在性能水平α划分下,系统(组件)的输出性能水平期望为[15]

(10)

此时,系统(组件)的输出性能水平期望为E(G(t))=p≤α(t)E≤α(G(t))+p>α(t)E>α(G(t)).

在性能水平α划分下,系统(组件)的u函数为[15]

(11)

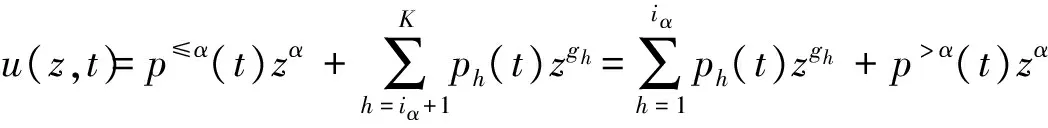
重要度表示由于系统中某个或多个组件发生失效或状态改变时,其对系统性能的影响程度,是时间、部件的可靠性参数以及系统结构的函数,可用于识别系统薄弱环节,提高系统可靠性[13,15- 16].在不同的系统或者同一系统中,分析对象或研究目的不同,重要度的定义也不同,下面详细介绍给定性能水平α下Birnbaum重要度、Fussell-Vesely重要度、风险业绩值(RAW)和风险降低值(RRW).

Birnbaum重要度又称概率重要度,描述了组件(状态)由>α性能水平值变为≤α性能水平值时,系统性能水平的变化值,即

(12)

Fussell-Vesely重要度描述组件(状态)性能对系统性能的贡献,表示为

(13)

组件(状态)≤α性能水平值被剔除后系统性能与原来系统性能的比值称为RAW,即

(14)

组件≤α性能水平被替换为完美性能时与系统≤α性能水平值的比值称为RRW,即

(15)

3 案例分析

由于组件2和3为同一类型元件,具有相同的性能状态和转移强度,因此它们的状态概率相同,只需求出一个组件即可,根据马尔可夫过程理论建立柯尔莫哥洛夫微分方程组,代入初始条件和全概率公式可求出各组件的状态概率,如图2所示,组件1的状态概率为p1(t)={p11(t),p12(t),p13(t),p14(t),p15(t)},组件2和组件3的状态概率为p2(t)={p21(t),p22(t),p23(t)}.

根据式(4)-(8)及通用生成函数法可分别得到系统及其组件的可靠度、性能状态期望值、性能状态驻留时间长度和性能状态平均期望值.由于篇幅有限,文中仅列出组件1的结果,如图3所示.

从图3(a)可知,系统在不同的性能要求下有不同的可靠度,系统性能要求越低,其可靠度越高;从图3(b)可知,在t=0时刻组件有最佳的性能,随着时间的延长,组件的性能状态逐渐迁移,在t=0.5 a后性能状态期望趋于稳定,约为3.3;从图3(c)可知,随着时间的延长,组件的性能逐渐退化,得到性能状态驻留时间长度后可估算出组件1的剩余使用寿命,如性能要求为大于状态1的输出性能水平,此时处在性能状态5,则可估算出剩余使用寿命区间[0.354 0,0.437 3].从图3(d)可知,平均性能水平期望值是一个归一化值,表征了系统及其组件的性能状态变化值,变化值越大说明系统退化程度越严重.

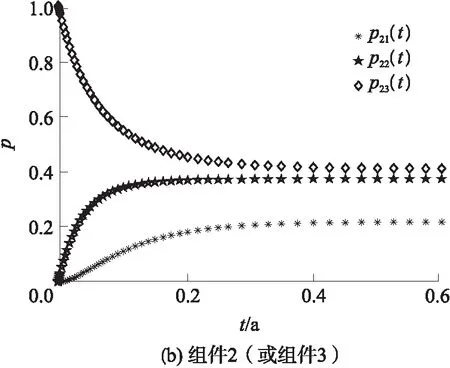
图2 各组件的状态概率

当任务时间T=1时,系统及其组件的状态概率和输出性能水平期望值见表1.其中系统为串-并联结构,并联关系为协同型,系统输出性能水平结构函数为G=min{u1(z,1),u2(z,1)+u3(z,1)},根据式(5)和(6)以及全概率公式可得系统共有8个性能状态,输出性能水平为G={0,20,25,40,50,60,75,80}.

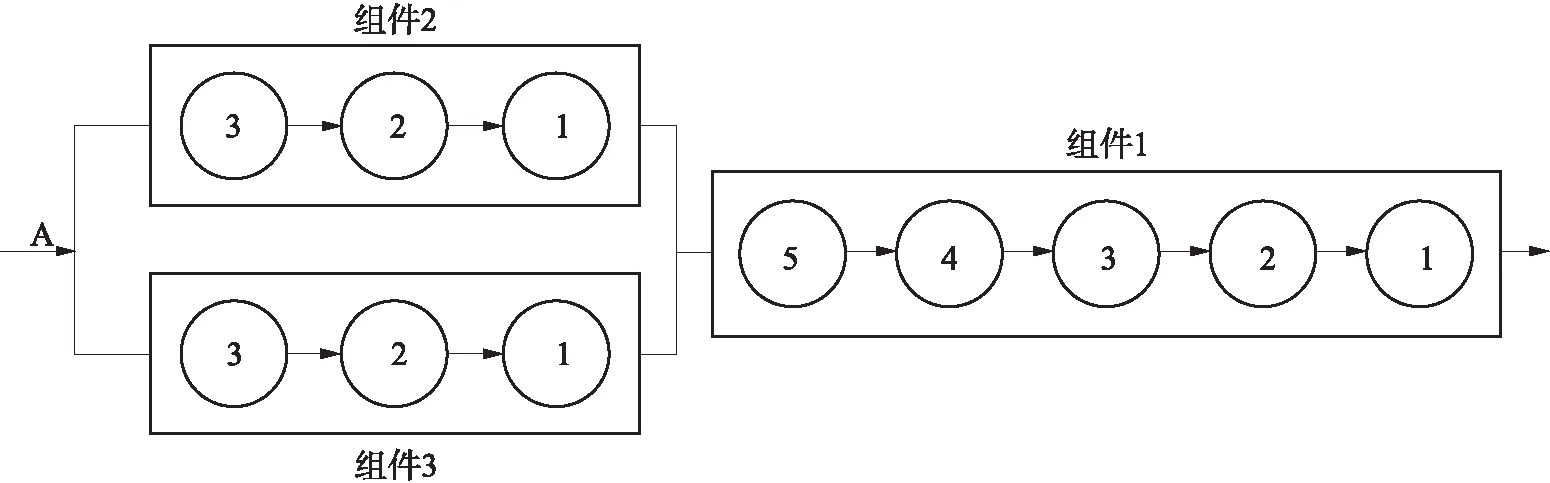
图1 四缸柴油机燃油供给系统的可靠性框图

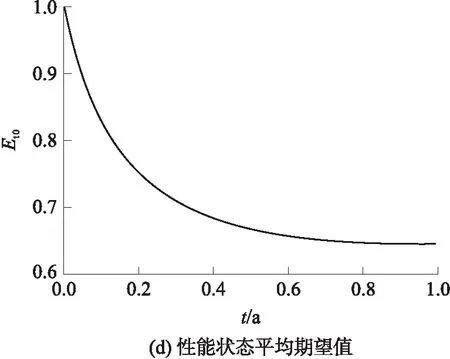
图3 组件1的可靠性度量

类型概率状态1状态2状态3状态4状态5状态6状态7状态8E(G(1))系统0．14690．14510．15420．22210．12390．13410．04420．029535．56组件10．10460．19500．26160．26290．1759〛55．26组件2/30．21740．37270．4099〛23．85

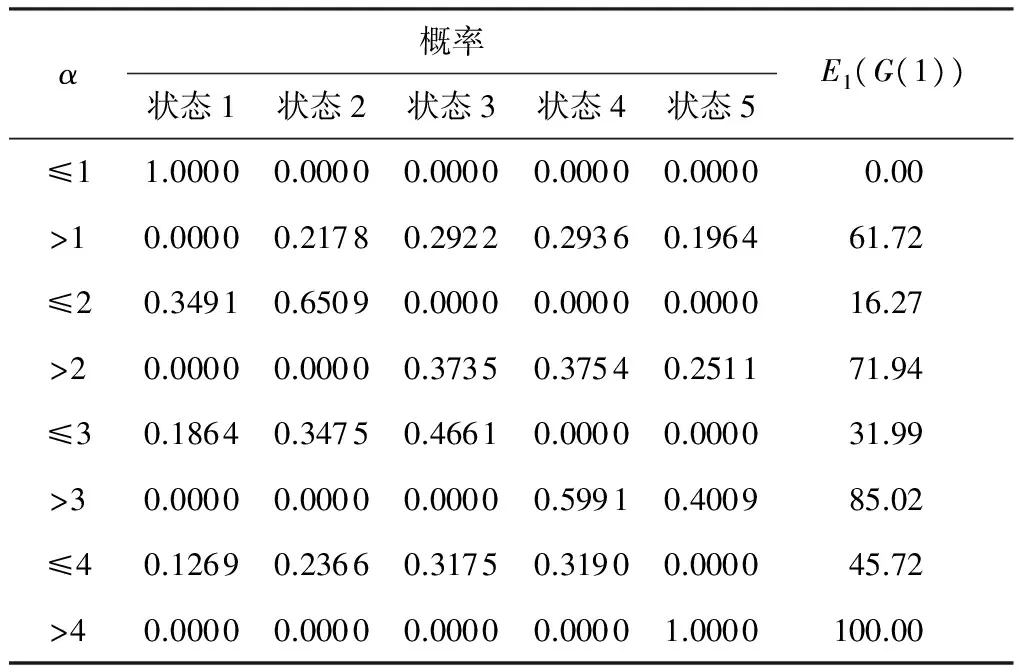
根据式(9)-(11)可求得在性能水平α划分下系统及其组件的状态概率和输出性能水平期望值,由于篇幅有限,仅列出在性能水平α划分下组件1的状态概率和输出性能水平期望,如表2所示.从表中可知,组件1有5个性能状态,性能阈值取1、2、3和4.可根据在不同划分水平下各状态的概率以及处于某性能水平划分下的输出性能水平确定各性能状态在系统(或组件)的地位,从而为可靠性分配提供理论参考.

根据式(12)-(15)可求得在性能水平α下系统及其组件的Birnbaum重要度、Fussell-Vesely重要度、RAW和RRW,如表3所示.

从表3可知:对于组件,从Birnbaum重要度、Fussell-Vesely重要度和RRW看,组件1比组件2(或3)重要;对于系统,从Fussell-Vesely重要度、RAW和RRW看,随着α的增大,性能状态重要度逐渐降低,而Birnbaum重要度反映了组件性能变化对整个系统的影响,性能状态重要性先降低后增加.根据上述4种重要度的计算结果,可以从多方面综合评估各组件(状态)对系统的影响,准确地确定各组件(状态)在系统所处的地位,识别出系统最薄弱的元件,为系统可靠性预测和分配、运行和维修、贮存和管理起着指导性作用.

表2 组件1在性能水平α划分下的状态概率及输出性能水平期望值

Table 2 State probability and output performance level expectation of component 1 under performance levelαrestriction

α概率状态1状态2状态3状态4状态5E1(G(1))≤11．00000．00000．00000．00000．00000．00>10．00000．21780．29220．29360．196461．72≤20．34910．65090．00000．00000．000016．27>20．00000．00000．37350．37540．251171．94≤30．18640．34750．46610．00000．000031．99>30．00000．00000．00000．59910．400985．02≤40．12690．23660．31750．31900．000045．72>40．00000．00000．00000．00001．0000100．00

表3 系统(组件)在性能水平α划分下的重要度

4 结论

(1)利用马尔可夫理论和通用生成函数法计算得到系统及其组件状态概率,一定程度上缓解了组合空间的爆炸问题.

(2)针对性能退化规律提出的新动态可靠性度量,能定量地反映系统及其组件的退化程度、所处状态以及各性能状态驻留时间长度,为可靠性诊断和预测提供了量化数据.

(3)在性能水平划分下求得系统及其组件状态概率和性能期望值,并用性能期望值定义重要度,有助于确定组件(状态)对系统的影响,识别出系统最薄弱环节,从而优化系统结构,提高系统可靠性.

[1] 杨庆芳,韦学武,林赐云,等.基于时空贝叶斯模型的行程时间可靠性预测 [J].华南理工大学学报(自然科学版),2016,44(4):115- 122. YANG Qing-fang,WEI Xue-wu,LIN Ci-yun,et al.Reliability prediction of travel time based on spatio-temporal bayesian model [J].Journal of South China University of Technology(Natural Science Edition),2016,44(4):115- 122.[2] LISNIANSKI A,FRENKEL I,DING Y.Multi-state system reliability analysis and optimization for engineers and industrial managers [M].London:Springer,2010.

[3] LISNIANSKI A,LEVITIN G.Multi-state system reliability,assessment,optimization and applications [J].Assessment Optimization & Applications World Scientific,2003,6:207- 237.

[4] LI J A,WU Y,LAI K K,et al.Reliability estimation and prediction of multi-state components and coherent systems [J].Reliability Engineering & System Safety,2005,88(1):93- 98.

[5] RAMIREZ-MARQUEZ J E,COIT D W,TORTORELLA M.A generalized multistate-based path vector approach to multistate two-terminal reliability [J].IIE Transactions,2006,38(6):477- 488.

[6] SORO I W,NOURELFATH M,AÏT-KADI D.Performance evaluation of multi-state degraded systems with minimal repairs and imperfect preventive maintenance [J].Reliability Engineering & System Safety,2010,95(2):65- 69.

[7] 高鹏,谢里阳.基于改进发生函数方法的多状态系统可靠性分析 [J].航空学报,2010,31(5):934- 939. GAO Peng,XIE Li-yang.Reliability analysis of multi-state systems based on improved universal generating function [J].Acta Aeronautica et Astronautica Siniga,2010,31(5):934- 939.

[8] ZIO E,MARELLA M,PODOFILLINI L.A Monte Carlo simulation approach to the availability assessment of multi-state systems with operational dependencies [J].Reliability Engineering & System Safety,2007,92(7):871- 882.[9] GU Y K,LI J.Multi-state system reliability:a new and systematic review [J].Procedia Engineering,2012,29:531- 536.

[10] LIU Y W,KAPUR K C.Reliability measures for dynamic multistate nonrepairable systems and their applications to system performance evaluation [J].IIE Transactions,2006,38(6):511- 520.

[11] 曾亮,郭欣.多状态系统元件重要度定义及其计算 [J].系统工程与电子技术,1999,21(5):71- 74. ZENG Liang,GUO Xin.The definition and computation method of component importance analysis in multistate system [J].Systems Engineering and Electronics,1999,21(5):71- 74.

[12] LI S,SI S,XING L,et al.Integrated importance of multi-state fault tree based on multi-state multi-valued decision diagram [J].Journal of Risk & Reliability,2014,228(2):200- 208.

[13] 古莹奎,承姿辛,李晶.性能水平划分下的多状态系统可靠性分析 [J].中国安全科学学报,2015,25(5):68- 74. GU Ying-kui,CHENG Zi-xin,LI Jing.Reliability analysis of multi-state system under performance level division [J].China Safety Science Journal,2015,25(5):68- 74.

[14] ZIO E,PODOFILLINI L.Importance measures of multi-state components in multi-state systems [J].International Journal of Reliability,Quality and Safety Engineering,2003,10(3):289- 310.

[15] LEVITIN G,PODOFILLINI L,ZIO E.Generalised importance measures for multi-state elements based on performance level restrictions [J].Reliability Engineering & System Safety,2003,82(3):287- 298.

[16] 古莹奎,李晶.基于多值决策图的多状态系统重要度分析 [J].中国安全科学学报,2014,24(6):44- 50. GU Ying-kui,LI Jing.Importance analysis of multi-state system based on multiple-valued decision diagram [J].China Safety Science Journal,2014,24(6):44- 50.

[17] JAFARY B,FIONDELLA L.A universal generating func-tion-based multi-state system performance model subject to correlated failures [J].Reliability Engineering & System Safety,2016,152:16- 27.

[18] 周金宇,谢里阳,韩文钦,等.可修系统剩余寿命分析的广义发生函数法 [J].兵工学报,2014,35(7):1103- 1109. ZHOU Jin-yu,XIE Li-yang,HAN Wen-qin,et al.Resi-dual life analysis of repairable systems based on universal generating function approach [J].Acta Armamentarii,2014,35(7):1103- 1109.

Dynamic Reliability Metric and Importance Analysis of Multi-State Systems

QIUGuang-qi1HUANGSi1GUYing-kui2

(1.School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China; 2. School of Mechanical and Electrical Engineering, Jiangxi University of Science and Technology, Ganzhou 341000, Jiangxi, China)

In order to characterize the reliability of multi-state system in performance degradation condition effectively and determine the effects of each component (state) on the system, this paper makes a performance state analysis and presents dynamic reliability metrics as well as an importance calculation method considering perfor-mance level restrictions. Firstly, the failure probability, reliability, performance state expectation, average performance state expectation and performance state duration of system (component) are calculated by using the universal generating function to avoid the combinatorial explosion of Markov model in multi-state system. Then, four importance indexes under certain performance level restrictions, namely Birnbaum importance, Fussell-Vesely importance, risk assessment worth and risk reduction worth, are defined with performance expectation value to comprehensively evaluate the effects of each component (state) on the system and meet different performance requirements of system (component). The application results to the fuel supply system of four-cylinder diesel engine indicate that the proposed approach can not only accurately solve the failure probability, reliability, performance state expectation, average performance state expectation and performance state duration of system (component), but also comprehensively assess the effects of each component (state) on the system according to the four importance values under performance level restrictions. Therefore, it helps improve system reliability through identifying the weakest parts in the system.

multi-state system; reliability;Markov processes; dynamic reliability metric; performance level restriction; importance

2016- 09- 12

国家自然科学基金资助项目(61164009,61463021) Foundation items: Supported by the National Natural Science Foundation of China(61164009,61463021)

邱光琦(1987-),男,博士生,主要从事系统可靠性优化及故障预测研究.E-smail:qiuguangqi@sina.cn

†通信作者: 黄思(1962-),男,教授,博士生导师,主要从事流体机械可靠性和数值计算研究.E-mail:huangsi@scut.edu.cn

1000- 565X(2017)05- 0052- 07

TB 114.3

10.3969/j.issn.1000- 565X.2017.05.008