线接触弹性磨损的数值分析*
占旺龙 黄平
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
线接触弹性磨损的数值分析*
占旺龙 黄平
(华南理工大学 机械与汽车工程学院, 广东 广州 510640)
磨损伴随在机械零部件的整个服役期内,对其寿命产生很大的影响.由于磨损是一个动态复杂的过程,现有的磨损研究主要集中在实验研究,这必然会增加成本及产品设计周期.为此,文中提出了一种基于Archard模型的数值计算方法,并用该方法对线接触弹性磨损全过程进行数值分析,最终得到不同滑动距离下的法向接触压力及磨损深度变化图.整个分析过程分步进行,即每计算一步都会更新表面接触形状,直至求出最大滑动距离下的磨损量.计算结果表明,在有摩擦力作用的情况下,对于线接触,接触压力会相对于初始接触点出现偏移,且摩擦系数越大,偏移越明显,接触宽度也会略微增大;在磨损过程中,接触状态会由线接触向面接触转化,压力分布的不对称性会逐渐减小,最终趋于对称分布.实验结果表明,数值预测值与实验值相一致.
磨损;线接触;接触压力;奇异积分方程;接触形状;数值分析
磨损是摩擦副在相对运动过程中一种连续的能量消耗及材料损耗过程.据报道,机械零部件的失效破坏有60%~80%是由磨损引起的.而现有对磨损的研究在很大程度上是通过实验进行的,即通过建立模拟实际工况条件的摩擦磨损模型,从而获得摩擦磨损的特性及变化趋势.不可否认实验方法具有较高的准确性,但由于需要制作实验模型,因此投入的成本较大且非常耗时.为了缩短产品设计周期,同时更好地设计机械零部件及预测其寿命,亟须建立适合于工程应用的磨损分析计算方法[1- 2].
由于磨损计算涉及到材料的物理化学性质、实际工况条件、磨屑损失及摩擦副形状等,因此相比于润滑计算中现成的Reynolds方程,磨损计算已经发展出针对不同工况条件下的若干计算公式[3- 5].其中形式简单且假设合理的Archard磨损模型成为使用最广泛的磨损计算模型.
Archard磨损模型可表述为磨损率与法向接触压力成正比,故确定接触区的大小及压力分布是磨损计算中最主要的任务.其中有限元法是用来求解接触压力最常用的方法[6- 9],虽然该方法可以比较精确地求解出接触压力分布,但其计算非常耗时.因此文献[10- 11]提出了Winkler模型,文献[12]提出了边界元法,但这些方法都没有考虑到摩擦力对接触压力分布的影响.因此,有必要探究滑动摩擦过程中摩擦力对磨损过程的影响.
通过数值模拟分析线接触弹性体磨损变化趋势最大的难点在于:通过变形逆解压力分布时的积分方程具有奇异性,在一般情况下很难甚至是不能得出其解析解,而求解其数值解的过程很容易出现不收敛的情况.此外,表面磨损具有时变性,即表面磨损会导致接触形状发生改变,从而影响接触压力分布,而接触压力改变反过来又会影响磨损率.因此,磨损计算分析是一个动态耦合过程,必须不断修改接触表面形状并计算得到与之相适应的压力来进行当前的磨损计算.
压力分布一旦确定,便可计算在不同滑动距离下的磨损量.Flodin等[11,13]计算了干摩擦直齿轮及斜齿轮在微量磨损情况下的磨损量.文献[14- 15]计算了混合润滑下线接触的磨损量.文献[10]计算了干摩擦情况下点接触的磨损量.这些计算结果表明,只要选择合适的磨损系数,便可计算在一定滑动距离下的磨损量[16- 17].
为此,文中提出了一种考虑摩擦力作用时计算接触压力的数值方法,以求解不同接触形状下的接触压力.首先阐述初始线接触情况下的磨损分析计算方法,然后推导出磨损计算中需要用到的基本方程,给出磨损量预测结果,并与实验值进行对比.
1 理论计算
1.1 基本方程
一般的接触形状最终都可以简化为点、线、面接触3种情况.文中以常见的线接触(环-块摩擦磨损实验)为例,两相对运动的线接触摩擦副接触表面可近似成弹性圆柱体与半平面之间的相对滑动问题,如图1所示.

图1 环-块摩擦磨损实验示意图
Fig.1 Schematic diagram of experiment for ring-block friction and wear
1.1.1 磨损量计算
摩擦副在运动过程中,接触表面磨损率dh/ds是坐标为x的点上法向接触压力p(x)的函数,其计算式为[18]
(1)
式中,k为磨损系数(单位为Pa-m),m为表面接触压力对磨损率的影响指数,它们可通过实验或计算求得[1,6,15,18].
根据Archard磨损定律,相对滑动距离为s时的磨损量为
(2)
在数值计算过程中,文中不考虑温度对磨损系数的影响,即认为在整个过程中磨损系数k保持不变.将接触界面进行离散化,假设接触界面上的节点编号为i(i=1,2,…,N),对时间进行离散后的编号为j(j=1,2,…,M),第i个节点在tj时刻的磨损量为h(i,j),此时该节点上的接触压力为p(i,j),相对滑动距离为Δs(i,j),则可得[19]
h(i,j+1)=h(i,j)+kpm(i,j)Δs(i,j)
(3)
由上述分析可知,要计算总相对滑动距离为s的总磨损量,则必须先求解在各个步长内的接触压力及磨损量.
1.1.2 压力计算
两相对滑动的摩擦副之间,除了存在法向载荷外,还存在因摩擦而传递的切向力.图2为在窄带上受任意分布的法向压力p(x)及切向力q(x)作用的弹性半空间,其中a1、a2为正数.
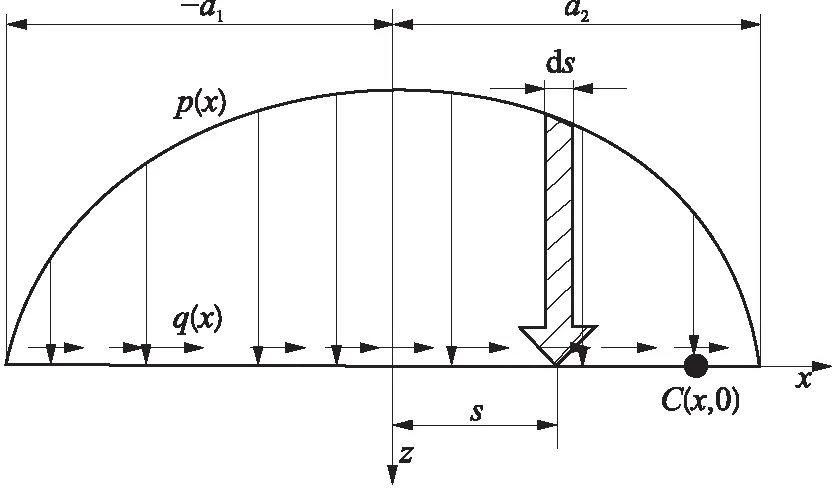
图2 接触表面的压力分布
根据弹性理论[20- 22],可求得表面上C点的法向位移为
(4)
式中,a1和a2分别为左、右接触区的接触宽度,E为弹性模量,ν为泊松比.对式(4)两边求x方向的导数,并代入q(x)=μp(x),可得[20]
(5)

此外,接触压力还需满足载荷平衡条件,即
(6)
L为单位长度的线载荷.
因此,若已知表面位移梯度,则可根据式(5)和式(6)确定法向力的分布情况.
1.1.3 表面位移梯度

(7)
式中,-a1≤xi≤a2,R为环的外径.由1.1.2节可知,求解接触压力时用到的参数为表面位移梯度,因此式(7)中的未知常数d不影响数值计算过程,而表面位移梯度可以采用中间差分法求得.
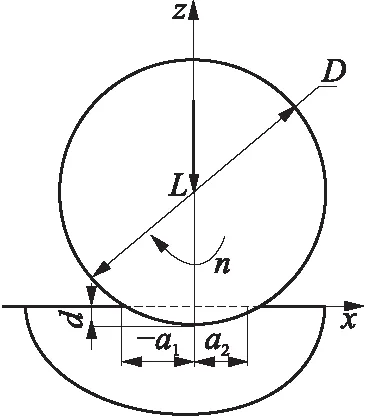
图3 摩擦力作用下刚性圆柱体与弹性半平面接触示意图
Fig.3 Diagram of contact between a rigid cylinder and an elastic half plane with friction
根据以上分析,数值磨损分析计算流程可按照图4进行.

图4 磨损计算流程图
1.2 数值实现
1.2.1 压力求解
由式(5)和式(6)可求解压力分布,但式(5)是含有柯西核的第二类奇异积分方程,国内外很多学者对其解法进行了较为深入的研究[23- 27],直接对奇异积分方程求解析解十分困难.因此,文中采用分段连续函数法[23- 24]来求解不同接触形状下的法向接触压力.
(8)
根据指数理论[24,28],方程(8)的解φ(X)可以写成基函数w(X)与有界函数g(X)的乘积形式,即φ(X)=w(X)g(X).定义基函数为
w(X)=(1-X)α(1+X)β
(9)
式中,α和β应满足Reα>-1,Reβ>-1.
若令a=μ(1-2ν),b=2(1-ν),且满足条件:

(10)
则式(8)中第一个方程可简化为
(11)
这样,就完全去掉了式(8)中第一个方程的奇异性,因为当T=X时,[g(T)-g(X)]/(T-X)=g′(X).最终对压力的求解可归结为对式(11)中g(X)的求解,X为配置点.原则上配置点可以选取除积分点以外的任意一点,但为方便计算,文中将配置点设置在积分点的中点.利用高斯-雅可比求积公式,将式(11)写成离散形式:
(12)
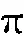
(13)
联立式(12)和(13)便可求解出g(Tj)(j=1,2,…,N+1),再通过φ(Tj)=w(Tj)g(Tj)可以求出未知函数φ(Tj)(j=1,2,…,N+1).另外,由于在计算之前并不知道接触区的大小,因此计算过程中应先给定一足够大的接触区,然后通过接触区内压力非负的条件来调整接触区大小,反复迭代计算,最终使压力和接触宽度满足载荷平衡条件和接触压力非负条件.
1.2.2 磨损求解
磨损是一个摩擦积累的动态耦合过程,为求解一定滑动距离下的磨损量,必须不断实时更新表面接触形貌并计算当前接触情况下的磨损量.在接触表面摩擦运动过程中,假设环为刚体,则以下数值计算过程只考虑块的磨损.
一旦确定法向接触压力分布,便可由式(3)求出相对滑动距离为Δs时接触区离散点上的磨损量,文中在计算过程中设定Δs为定值,即每经过相同的Δs更新一次接触压力及形貌.计算过程中由于高斯点不变而接触宽度发生变化,因此会造成不同积分步上积分点不重叠的情况,因此计算当前接触形貌时无法直接使用上一次磨损量,文中采用如下处理方法:先将上一次实际接触宽度映射到当前积分步上,映射区域内离散点上的磨损量采用样条插值的方法进行拟合,而映射区域以外的区域将磨损量置为0.
2 结果与讨论
2.1 实验参数及条件
磨损试验在MRH-3高速环块摩擦磨损试验机上进行,实验过程中保持法向载荷恒定.磨损痕迹通过TALYSURF CLI 1000表面形貌仪测量.环材料为06Cr19Ni10(不锈钢),块材料为45#钢,其材料性能参数如下:弹性模量为200 GPa,泊松比为0.3.环块样品根据GB/T 12444—2006进行制备.环直径为49.22 mm,宽为13.06 mm;块长×宽×高为19.05 mm×12.32 mm×12.32 mm.为消除磨损过程中温度对磨损系数的影响,试验机设定为较低转速,具体运行参数为:转速100 r/min,温度(25.5±3)℃,载荷123 N.
2.2 数值预测及分析
用数值方法计算在不同摩擦系数下的压力分布、接触宽度及接触半宽比(a2/a1),结果如图5所示.由图5(a)可知,当摩擦系数增大时,接触区载荷分布的不对称性越明显,但峰值压力几乎不会发生改变.由图5(b)可知:随着摩擦系数的增大,接触宽度会略微增大,摩擦系数为1(工程中摩擦系数一般不会大于1)时,相比Hertz接触宽度也仅增大1.6%;虽然摩擦力对峰值压力及接触宽度的影响很小,但对接触区的位置的影响很大,摩擦系数为1时,接触区中点相对于初始接触点偏移了17.7%.


图5 不同摩擦系数下的接触压力、接触宽度及右/左接触半宽比
Fig.5 Contact pressure,contact width and the ratio of right contact width to left with different friction coefficients
图6给出了接触压力随磨损距离的变化情况.计算参数如下:影响指数m=1,磨损系数k=4.8×10-17Pa-1,摩擦系数μ=0.12,计算步长为100 μm.由图中可知,随着磨损距离的增加,接触压力迅速下降并近似趋于均匀分布.图中内嵌图为局部压力放大图,由图中可知,在接触边界处会出现局部压力峰值.此结果与文献[6]的有限元法计算结果一致.为提高计算效率,文中在后续计算中采用简化方法,即当接触宽度大于初始接触宽度的2.5倍时,可近似认为接触压力为均布载荷.

图6 接触压力随磨损距离的变化
图7为不同滑动距离下的磨损深度预测图.图8给出了峰值压力和接触宽度随磨损距离的变化情况,由图中可知,随着磨损距离的增大,峰值压力开始迅速减小,而后趋于线性减小,接触宽度也由开始时的快速增加变为平稳增加.图9给出了最大磨损深度随磨损距离的变化情况,开始时最大磨损深度变化较大,而后最大磨损深度与磨损距离近似为线性关系.这主要是由于接触状态由线接触向面接触转变而引起的.

图7 不同滑动距离下的磨损形貌预测
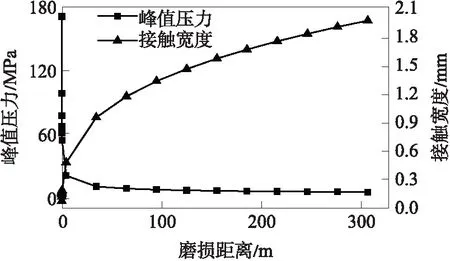
图8 峰值压力及接触宽度随磨损距离的变化
Fig.8 Variation of maximum contact pressure and contact width with wear distance

图9 最大磨损深度随磨损距离的变化
2.3 实验结果及分析
文中进行磨损距离分别为75、150、225和300 m的磨损试验,摩擦系数与温度变化统计结果如图10所示,其中直方图表示平均值,误差线为统计标准差.由图中可知,在整个磨损过程中,摩擦系数和温度都保持在相对稳定值.
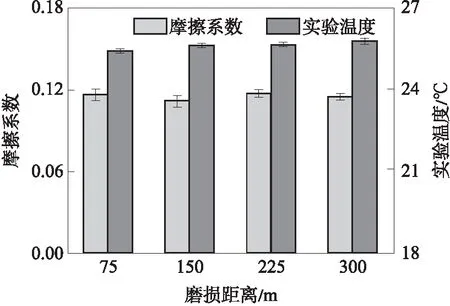
图10 不同磨损距离下的摩擦系数与温度统计结果
不同滑动距离和磨损距离(75、150、225和300 m)下,磨损深度的理论预测值与实验结果对比
如图11所示,由图中可知,不同磨损距离下的磨损量预测值与实验结果吻合较好.
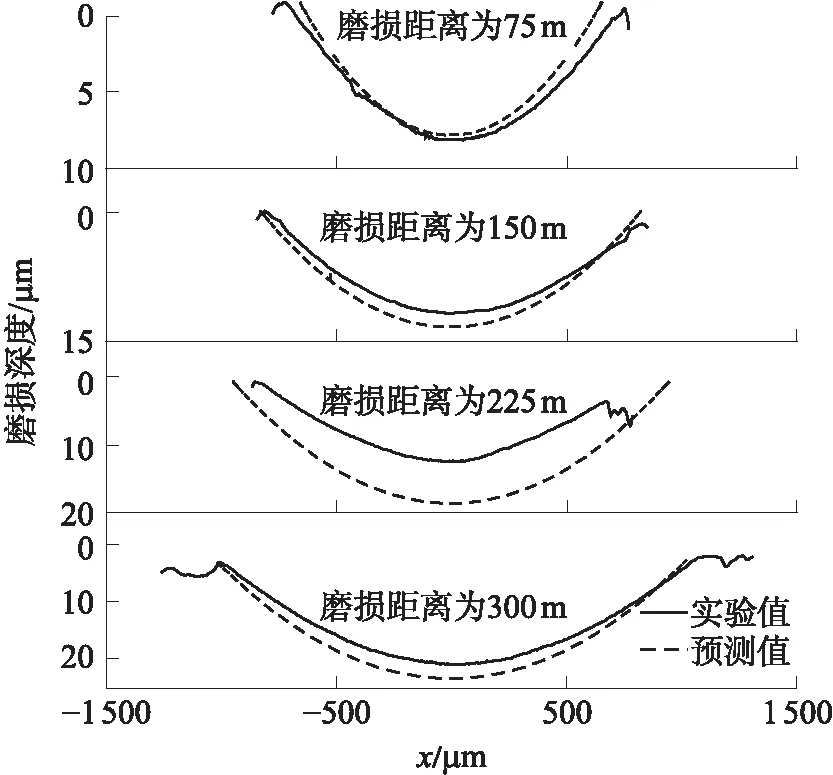
图11 磨损深度的预测值与实验值对比
Fig.11 Comparison of wear height between numerical prediction values and experimental values
3 结论
文中以环-块磨损实验为模型,提出了基于Archard模型的接触压力数值计算方法,并用该方法对初始线接触弹性变形条件下的微量磨损进行分析,得出主要结论如下:
(1)通过求解第二类奇异积分方程,可以得到存在摩擦力情况下任意接触形状的接触压力;
(2)通过计算发现,对于线接触,接触压力会相对于初始接触点出现偏移,且摩擦系数越大,偏移越明显,并且接触宽度会有略微的增大;
(3)在磨损过程中,接触状态会由线接触向面接触转化,峰值压力在磨损初始阶段迅速锐减,而在后期变化缓慢,压力分布的不对称性会逐渐减小,最终趋于对称分布.
文中在计算磨损量过程中考虑了摩擦力对压力的影响,从而分析了弹性变形下的接触磨损过程.理论上只要给定一合适的磨损系数(可以为常数,亦可为滑动距离的函数),便可使用文中方法分析任意滑动距离下的磨损变化趋势.这为当前磨损研究中实验方法偏多而理论计算方法偏少的现象提供了有力的补充.
[1] 温诗铸,黄平.摩擦学原理 [M].4版.北京:清华大学出版社,2012.
[2] FARAH P,GITTERLE M,WALL W A,et al.Computational wear and contact modeling for fretting analysis with isogeometric dual mortar methods [J].Key Engineering Materials,2016,681:1- 18.
[3] MENG H C,LUDEMA K C.Wear models and predictive equations:their form and content [J].Wear,1995,181:443- 457.
[4] WILLIAMS J.Wear modelling:analytical,computational and mapping:a continuum mechanics approach [J].Wear,1999,225/226/227/228/229:1- 17.
[5] WILLIAMS J A.Wear and wear particles:some fundamentals [J].Tribology International,2005,38(10):863- 870.
[6] MCCOLL I,DING J,LEEN S.Finite element simulation and experimental validation of fretting wear [J].Wear,2004,256:1114- 1127.
[7] PODRA P,ANDERSSON S.Simulating sliding wear with finite element method [J].Tribology International,1999,32(2):71- 81.
[8] MUKRAS S,KIM N H,SAWYER W G,et al.Numerical integration schemes and parallel computation for wear prediction using finite element method [J].Wear,2009,266:822- 831.
[9] HEGADEKATTE V,HUBER N,KRAFT O.Finite element based simulation of dry sliding wear [J].Modelling and Simulation in Materials Science and Engineering,2004,13(1):57- 75.
[11] FLODIN A,ANDERSSON S.Simulation of mild wear in spur gears [J].Wear,1997,207:16- 23.
[12] SFANTOS G,ALIABADI M.Wear simulation using an incremental sliding boundary element method [J].Wear,2006,260:1119- 1128.
[13] FLODIN A,ANDERSSON S.Simulation of mild wear in helical gears [J].Wear,2000,241:123- 128.
[14] BRAUER J,ANDERSSON S.Simulation of wear in gears with flank interference:a mixed FE and analytical app-roach [J].Wear,2003,254:1216- 1232.
[15] HAO L C,MENG Y G.Numerical prediction of wear process of an initial line contact in mixed lubrication conditions [J].Tribology Letters,2015,60(2):1- 16.
[16] 罗双强.线接触滑/滚复合磨损实验和理论研究 [D].长春:吉林大学,2016.
[17] GHOSH A,SADEGHI F.A novel approach to model effects of surface roughness parameters on wear [J].Wear,2015,338/339:73- 94.
[18] KRAGELSKY I V,DOBYCHIN M N,KOMBALOV V S.Friction and wear:calculation methods [M].Oxford:Pergamon,1982.
[19] 张方宇,桂良进,范子杰.销-盘试验的热-应力-磨损耦合模拟研究 [J].机械工程学报,2015,51(8):107- 115. ZHANG Fang-yu,GUI Liang-jin,FAN Zi-jie.Study on simulation of coupled heat transfer,stress and wear behavior in pin-on-disc experiments[J].Journal of Mechanical Engineering,2015,51(8):107- 115.
[20] JOHNSON K L.Contact mechanics [M].Cambridge:Cambridge University Press,1985.
[21] 徐芝纶.弹性力学 [M].北京:高等教育出版社,2006.
[22] 黄平,赖添茂.基于真实接触面积的摩擦模型 [J].华南理工大学学报(自然科学版),2012,40(10):109- 114. HUANG Ping,LAI Tian-mao.Friction model based on real contact area [J].Journal of South China University of Technology(Natural Science Edition),2012,40(10):109- 114.
[23] GERASOULIS A.The use of piecewise quadratic polynomials for the solution of singular integral equations of Cauchy type [J].Computers & Mathematics with Applications,1982,8(1):15- 22.
[24] JIN X,KEER L M,WANG Q.A practical method for singular integral equations of the second kind [J].Engineering Fracture Mechanics,2008,75(5):1005- 1014.
[25] CHEN Z,WANG C,ZHOU Y.A new method for solving Cauchy type singular integral equations of the second kind [J].International Journal of Computer Mathema-tics,2010,87(9):2076- 2087.
[26] BEYRAMI H,LOTFI T,MAHDIANI K.A new efficient method with error analysis for solving the second kind Fredholm integral equation with Cauchy kernel [J].Journal of Computational and Applied Mathematics,2016,300:385- 399.
[27] GERASOULIS A,SRIVASTAV R.A method for the numerical solution of singular integral equations with a principal value integral [J].International Journal of Engineering Science,1981,19(9):1293- 1298.
[28] MUSKHELISHVILI N I,RADOK J R M.Singular integral equations:boundary problems of function theory and their application to mathematical physics [M].2nd ed.Massachusetts:Courier Corporation,2008.
[29] HALE N,TOWNSEND A.Fast and accurate computation of Gauss-Legendre and Gauss-Jacobi quadrature nodes and weights [J].SIAM Journal on Scientific Computing,2013,35(2):A652- A674.
Numerical Analysis of Elastic Wear in Line Contact
ZHANWang-longHUANGPing
(School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, Guangdong, China)
Wear exists in the whole service lifetime of mechanical parts and produces great impact on the lifetime of a machine. Current researches on wear mainly focus on experiments due to the dynamic complexity of wear process, which may increase the production cost and the product design cycle. In order to solve this problem, an Archard’s model-based numerical method is proposed, which is used to numerically analyze the whole process of elastic wear in line contact and obtain the normal contact pressure as well as wear depth at different sliding distances. The simulation process is conducted step by step, i.e., in each step, the surface contact topography is updated until the maximum sliding distance is achieved. Calculated results show that, for line contact, the contact pressure offsets with respect to the initial contact point at which friction force exists, and the offset becomes obvious as the friction coefficient increases, at the same time, the contact width increases slightly. Moreover, it is found that, in wear process, the contact state transfers from line contact to surface contact, and the asymmetry of contact pressure distribution gradually diminishes till to a symmetrical state. Experimental results show that the numerical prediction values are consistent with the experimental ones.
wear; line contact; contact pressure; singular integral equation; contact topography; numerical analysis
2016- 10- 26
国家自然科学基金资助项目(51575190) Foundation item: Supported by the National Natural Science Foundation of China(51575190)
占旺龙(1992-),男,博士生,主要从事摩擦学设计及理论研究.E-mail:mezhanwl@mail.scut.edu.cn
1000- 565X(2017)05- 0045- 07
TH 117.1
10.3969/j.issn.1000-565X.2017.05.007

