多传感信息融合机器人标定方法
张湧涛,金 爽,王 一
(华北理工大学电气工程学院,河北 唐山 063009)
多传感信息融合机器人标定方法
张湧涛,金 爽,王 一
(华北理工大学电气工程学院,河北 唐山 063009)
该文提出一种基于多传感信息融合技术进行机器人运动学标定的方法。首先通过对机器人的指数积(POE)正向运动学模型取微分的方式建立末端执行器的误差模型,利用ROMER-RA7520绝对关节臂测量机和安装在末端工具上的多个传感器分别采集末端执行器的位置和姿态信息;随后根据坐标统一原理将测量机的位置测量数据和多传感器的姿态量测数据转换到机器人基础坐标系下,实现位姿数据的空间配准;接着运用自适应加权融合算法融合处理经过空间配准后的位姿数据,得到末端执行器位姿测量值;最后应用迭代最小二乘法求解出参数偏差。KR5arc机器人标定仿真实验表明:该方法可大幅度提升机器人在任意位姿下的定位、定姿精度。
指数积;测量臂;空间配准;多传感信息融合;参数标定
0 引 言
工业机器人由于受机构本身加工、装配误差以及日常使用过程中的磨损等因素的影响,其绝对定位精度仅达毫米级,无法达到一些工业生产中对定位精度的要求。因此,如何有效消除或减小这些误差,成为机器人在精密加工领域应用所面临的首要问题。采用高精度的生产设备来提高机器人零部件的加工精度是提高机器人定位精度的有效方法,但成本太高,而通过修改机器人的运动学参数来提升其绝对定位精度是一种行之有效的方法,并且比较容易实现[1-3]。
机器人标定按照是否需要建立运动学模型分为两类:运动学模型标定和自标定。运动学模型标定方法一般由误差建模、测量、辨识和补偿4个环节组成[4]。国内外学者对于机器人运动学标定问题已经展开了研究工作,如从建模方法出发,旨在建立更为准确且参数连续的运动学模型;其中,D-H参数模型由于在计算过程中所需的参数个数最少,因而得到了广泛应用,但D-H参数模型也有其局限性,表现在当相邻关节的轴线近乎平行时模型存在奇异性问题。对此,一些学者提出了改进的D-H参数模型或其他的参数模型来解决该问题,但也带来了建模过程复杂、缺少通用性等新问题[5-6]。Park针对串联机器人提出了一种指数积模型,不仅实现了转动关节与移动关节的统一描述,而且运动学参数关于关节轴的变化是连续、光滑的,避免了D-H参数法存在的奇异性问题[7]。也有研究将目光集中于位姿测量方法,如利用激光跟踪仪、三坐标测量机等高精度测量设备获得机器人实际位姿,该方法测量精度高,但只能测量给定点的位姿信息且成本较高。或通过将机器人工作空间离散化,建立空间网格精度模型的方法对位置和姿态分别进行标定,该方法只能确保机器人在被标定空间内具有较好的标定效果。
近年来,多传感信息融合技术以其观测范围广、提供的信息可信度高、可进行在线实时测量以及成本低等优点受到广泛关注,并在状态监测与故障检测、空间目标识别与跟踪、机器人避障与导航以及图像处理等领域发挥了重要的作用[8]。本文提出将该项技术应用于机器人运动学参数标定,通过分析探究数据融合过程中涉及的量测数据预处理技术以及融合算法的选择实现提升机器人定位精度的目的。
1 误差模型线性化
n自由度串联结构机器人正向运动学的指数积(POE)公式为

θi——第i个关节的关节变量;
gst(0)——各关节均处于零位时按基础坐标系描述的末端执行器的位姿矩阵。
gst(0)还可以表示为某个常旋量st∈se(3)的指数形式,则式(1)可改写为

假设机器人的各个关节均存在运动学参数误差,并用δξ、δξst和δθ分别代表关节旋量坐标偏差、初始位姿变换旋量坐标偏差和关节变量零位偏差,对式(2)取微分可得误差模型:
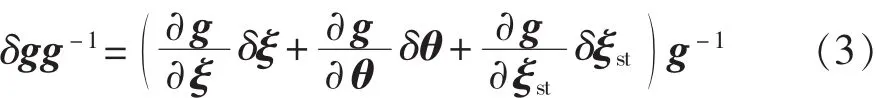
其中:
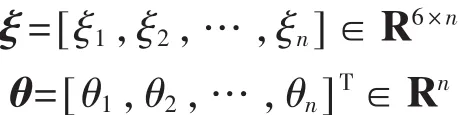
关节变量零位偏差可看作是旋量坐标偏差的一个误差源,无需单独辨识[7]。因此,误差模型(3)可简写为
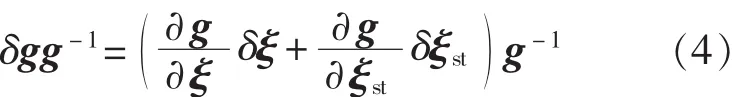
将式(2)代入误差模型式(4)中,经过化简可知:




将式(6)、式(7)代入式(5)可知(δg·g-1)∨的显式表达式为

对于式(4)的左侧,令ga为测量得到的机器人末端执行器的实际位姿,gn为末端执行器名义位姿,则δgg-1反映了按基础坐标系描述的从ga到gn的偏差,当两者相差足够小时存在如下关系:

2 多传感信息融合
多传感信息融合流程如图1所示,通常由原始数据采集、量测数据预处理、数据关联、数据决策以及信息融合5个阶段构成[8]。假如传感器的量测数据均来自于同一被测目标,则不必对其实施数据关联和数据决策。

图1 多传感器信息融合流程图
2.1 量测数据预处理和坐标统一
2.1.1 量测数据预处理
在本文设计的多传感器信息融合系统中,各传感器的初始采样时刻、采样频率设置相同,并且假设通信网络的传输延迟可忽略,则该融合系统的量测数据可看作是同步的,不必进行时间配准。此外,由于参与融合的各传感器量测数据都是相对于自身坐标系描述的,因此需要将其转化到机器人基础坐标系中,即对其进行空间配准[11]。
多传感器量测数据空间姿态配准实验设计如下:设末端执行器在机器人基础坐标系下和传感器坐标系下的姿态角分别为ra和rb,则两者之间的变换关系可表示为

其中 ra=(γa,βa,αa)T,rb=(γb,βb,αb)T,R 为传感器坐标系与机器人基础坐标系之间的姿态变换矩阵。
R的数学表达式确定原理为:若传感器相对于机器人基础坐标系的偏转角、俯仰角和侧倾角分别为Φ、η和φ,则传感器坐标系与机器人基础坐标系之间的姿态变换矩阵可表示为

该矩阵为正交矩阵,即满足:

2.1.2 位置坐标统一
机器人的位置信息是通过ROMA-RA7520绝对关节臂测量机实现。位置坐标统一实验设计如下:首先驱动机器人运动到工作空间中的一系列标定位姿,通过控制器读取并记录机器人处于各个位姿时所对应的末端执行器位置理论值;然后利用测量机探测不同位姿所对应的末端执行器位置测量值,由于测量臂具很高精度,因此可认为该测量值即为在测量臂坐标系下描述的末端执行器位置实际值;最后根据坐标同一原理建立测量臂坐标系与基础坐标系之间的齐次变换矩阵,将测量臂坐标系下的量测数据转化到机器人基础坐标系下,即可得到相对于基础坐标系描述的末端执行器位置实际值。
坐标统一原理为:假设空间中某点在直角坐标系OaXaYaZa下的坐标向量为 Pa=(xa,ya,za)T,在直角坐标系 ObXbYbZb下的坐标向量为 Pb=(xb,yb,zb)T,则两者之间的坐标变换可表示为

Tab=[txtytz]T——描述位置的平移向量。

式(14)给出了6个正交约束方程,故式(13)提供3组或3组以上坐标向量即可确定位姿变换矩阵Hab。
位置坐标统一实验设计如下:首先驱动机器人运动到工作空间中的一系列标定位姿,然后通过控制器读取并记录机器人处于各个位姿时所对应的末端执行器位置理论值,接着利用测量机探测不同位姿所对应的末端执行器位置测量值,由于测量臂是一种高精度的测量设备,因此可认为该测量值即为在测量臂坐标系下描述的末端执行器位置实际值,最后根据坐标同一原理建立测量臂坐标系与基础坐标系之间的齐次变换矩阵,将测量臂坐标系下的量测数据转化到机器人基础坐标系下,至此,即可得到相对于基础坐标系描述的末端执行器位置实际值。
2.2 信息融合
目前,信息融合算法主要包括加权平均法、卡尔曼滤波法、D-S证据理论、Bayes推理法、神经网络等。本文在分析了现有融合算法特点的基础上,提出采用自适应加权融合算法[12]对经过配准的传感器量测数据进行融合处理。自适应加权融合算法模型如图2所示。

图2 自适应加权融合算法模型
图中,X1,X2,…,Xn表示 n 个传感器对于同一对象相同参数的量测数据,为加权融合后的值。
2.2.1 最优加权因子及其方差
假设测量系统由两个传感器组成,传感器A和B的方差分别为σ12和σ22,且对应的加权因子分别为W1和W2,X1和X2为两传感器的量测数据,两者相互独立且都是真值X的无偏估计。由于待估真值X为常量,因此需通过传感器历史量测数据的均值来估计对象参数的真值,即存在如下关系:

式中:m——传感器i的历史量测数据的个数;
引进加权因子W1和W2后,两传感器量测数据的融合结果为

此时,传感器系统总方差为
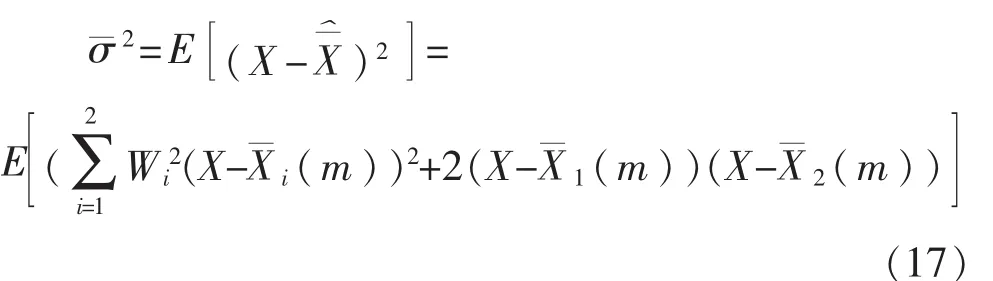
由于 X1和X2都是真值X 的无偏估计,因此1(m)和2(m)同样满足这一条件,则式(17)可简写为

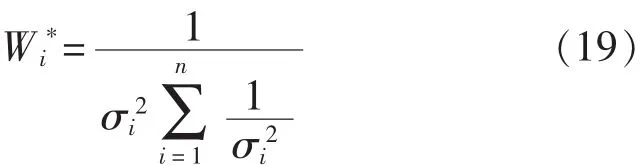
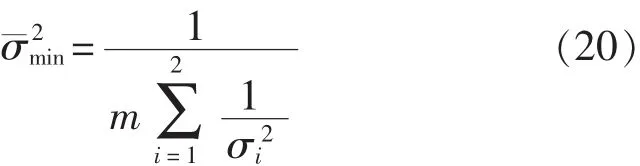
2.2.2 最优加权因子的求取
由式(19)可知,求取最优加权因子的前提是先求得各传感器的方差,而方差σi2可根据各传感器的测量值,通过计算得到。设两相互独立传感器的测量误差分别为ei和ej,则测量值Xi和Xj可用下式表示:

其中ei和ej为零均值高斯白噪声。
则两传感器的方差可表示为

由于两传感器相互独立且ei和ej为零均值高斯白噪声,故Xi和Xj的互协方差函数Rij可化简为
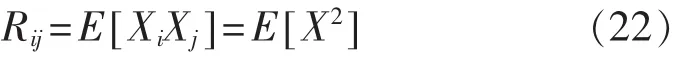
Xi和Xj的自协方差函数Rii满足:
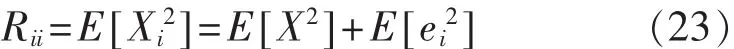
由式(22)、式(23)可知式(21)改写为

式中Rii和Rij可由各自的时间域估计值确定。
假设 Rii(k)和 Rij(k)分别代表 Rii和 Rij的时间域估计值,则有:

同理可知:

3 参数辨识
式(8)可写成如下矩阵形式:

式中:
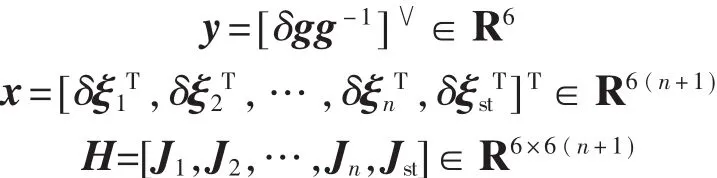
矩阵H中的各项具有如下形式:

驱动机器人运动到工作空间中的m个测量位姿,将产生m组形如式(27)的误差方程,将此m组误差方程合并即可得到标定方程组:

其中:

旋量坐标误差可由迭代最小二乘法解得:

4 参数标定流程
控制机器人运动到工作空间中的m个标定位姿,通过控制器读取各关节变量值,并代入式(1)计算末端执行器位姿名义值,通过融合处理多个传感器提供的量测数据获得末端执行器位姿测量值,参数迭代识别过程中,将旋量坐标名义值作为迭代计算初值,关节旋量坐标偏差δξi和初始位姿变换旋量坐标偏差δξst可根据式(29)确定,最后按照图 3所示迭代识别过程完成旋量坐标辨识。为保证更新后的关节旋量坐标仍然满足关节约束条件,需要在每次迭代计算过程中对旋量坐标进行一次正交化处理。
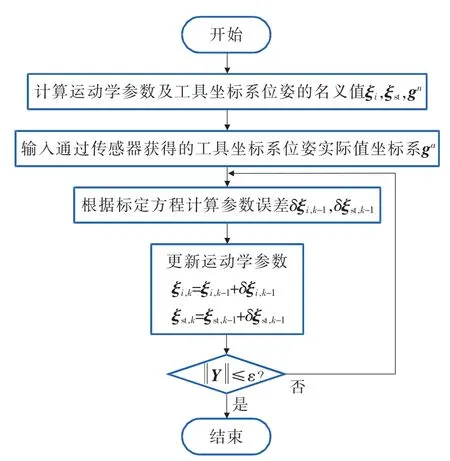
图3 参数迭代识别过程
5 标定实验
为了检验参数标定方法的有效性,通过KR5arc串联机器人标定实验进行验证。KR5arc机器人由刚性连杆以及连接相邻连杆的6个转动关节和基座构成,机器人的初始关节角度 θ1~θ6依次为 0°,90°,-90°,0°,0°,0°,机器人连杆参数如图4所示,由此可计算出各关节旋量坐标的理论值如表1所示。
首先驱动机器人运动到工作空间中的50个标定点,通过控制器读取和记录每个标定点所对应的关节角度值,并根据表2所示旋量坐标的理论值,按式(2)计算末端执行器的名义位姿,计算此50个标定点处所对应的多传感器系统的融合输出值,最后按照图3所示迭代识别过程完成旋量坐标辨识,并根据辨识结果修正机器人的运动学参数。参数迭代识别过程中,以旋量坐标名义值为计算初值,辨识结果如表1所示。

图4 KR5arc机器人连杆参数(单位:mm)
1)姿态校准效果验证实验。首先,在机器人的工作空间中随机取30个标定点以外的点作为验证点,利用航姿参考系统和双轴倾角传感器采集这30个点处的机器人姿态信息并对其进行融合处理,将融合结果作为机器人姿态角实际值;根据式(2)及表1所示旋量坐标理论值解算出这30个点在基础坐标系下的姿态角理论值,然后解算出补偿后的姿态角;最后分别将标定前和标定后机器人的姿态角与其实际值做差可得姿态校准效果图,如图5所示。
2)位置校准效果验证实验。①对上述30个验证点进行编号,测量其在测量臂坐标系下的坐标,并按照编号顺序依次计算相邻两点之间的距离,由于测量臂是一种高精度的测量设备,因此可将其测量结果作为真实值;②根据式(2)以及表1所示旋量坐标理论值计算这30个点在基础坐标系下的位置理论值,并按照编号顺序依次计算相邻两点之间的距离;③根据式(2)以及表1所示旋量坐标辨识结果计算补偿后这30个点在基础坐标系下的位置坐标,并按照编号顺序依次计算相邻两点之间的距离;④将①与②计算得到的结果做差可知标定前机器人的距离误差,将①与③计算得到的结果做差可知标定后机器人的距离误差,结果如图6所示。

表1 旋量坐标值
6 结束语
本文基于指数积公式建立了机器人的正向运动学模型,该模型避免了D-H参数法存在的奇异性问题,实现了转动关节与移动关节的统一描述。首先通过测量机和安装在末端工具上的多个传感器分别采集末端执行器的位置和姿态信息,然后根据坐标统一原理将测量机的位置测量数据和多传感器的姿态量测数据转换到机器人基础坐标系下,实现量测数据的空间配准,接着根据自适应加权融合算法对经过配准后的量测数据进行融合处理,该算法可确保融合后传感器系统的总方差小于组成测量系统的各传感器的方差。最后通过KR5arc串联机器人标定仿真实验验证了标定方法的有效性。
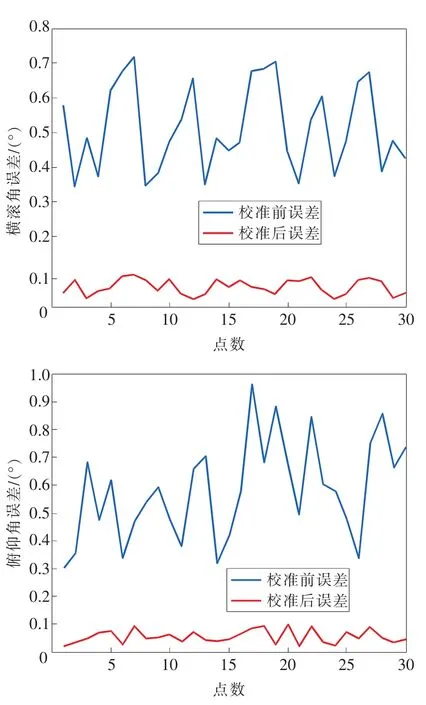
图5 姿态角校准效果图

图6 KR5arc机器人距离校准效果图
[1]高文斌,王洪光,姜勇,等.基于距离误差的机器人运动学参数标定方法[J].机器人,2013,35(5):600-606.
[2]陈钢,贾庆轩,李彤,等.基于误差模型的机器人运动学参数标定方法与实验[J].机器人,2012,34(6):680-688.
[3]李睿,曲兴华.工业机器人运动学参数标定误差不确定度研究[J].仪器仪表学报,2014,35(10):2192-2199.
[4]XUAN J Q,XU S H.Review on kinematics calibration technology of serial robots[J].International Journal of Precision Engineering and Manufacturing,2014,15 (8):1759-1774.
[5]VEITSCHEGGER W K,WU C H.Robot accuracy analysis based on kinematics[J].IEEE Journal on Robotics and Automation,1986,2(3):171-179.
[6]ZHUANG H, ROTH Z S, HAMANO F.A complete and parametrically continuous kinematic model for robot manipulators[J].IEEE Transactions on Robotics and Automation,1992,8(4):451-463.
[7]高文斌,王洪光,姜勇.一种基于指数积的串联机器人标定方法[J].机器人,2013,35(2):156-161.
[8]蒋雅娜,王帮峰,李迎,等.多传感器信息融合技术及其在智能材料结构中的应用[J].中国测试技术,2003,29(5):22-23.
[9]HE R B, ZHAO Y J, YANG S N.Kinematic-parameter identification for serial-robot calibration based on POE formula[J].IEEE Transactions on Robotics,2010,26(3):411-423.
[10]LOU Y J, CHEN T N, WU Y Q, et al.Improved and modified geometric formulation of POE based kinematic calibration of serial robots[C]∥IEEE/RSJ International Conference on Intelligent Robots and Systems Piscataway NJ USA: IEEE,2009:5261-5266.
[11]叶宏.多传感器系统配准算法研究[D].绵阳:中国工程物理研究院,2014.
[12]丁辉,仲跃,张俊,等.基于相关性函数的多传感器自适应加权融合算法 [J].重庆理工大学学报 (自然科学版),2016,30(2):114-118.
(编辑:莫婕)
Robot calibration method based on multi-sensor information fusion
ZHANG Yongtao,JIN Shuang,WANG Yi
(College of Electrical Engineering,North China University of Science and Technology,Tangshan 063009,China)
A method of robot kinematics calibration based on multi-sensor information fusion technology is proposed.Firstly,an error model of end effector is established by differentiating the POE forward kinematics model of robot,and then ROMER-RA7520 absolute articulated arm measuring machine and many sensors mounted at the end tool are used to collect the end effector position and attitude information.After that,the position measurement data of the measuring machine and the attitude measurement data of multi-sensor will be converted to the robot base coordinate system according to unity principle of the coordinate to realize the special alignment of position and attitude data.And then,the adaptive weighted fusion algorithm is used to have fusion processing of the position and attitude data after special alignment and get the measured position and attitude data of end effector.Finally, iterative least square method is used to get the parameter deviation.KR5arc robot calibration simulation experiment shows that the method can greatly improve the positioning and attitude determination accuracy of the robot under any position and attitude.
product of exponential; measuring arm; space alignment; multi-sensor information fusion;parameter calibration
A
1674-5124(2017)04-0056-07
10.11857/j.issn.1674-5124.2017.04.013
2016-09-18;
2016-10-25
国家自然科学基金青年科学基金项目(51505125)
张湧涛(1958-),男,河北唐山市人,教授,主要从事检测技术及智能装置、控制理论在过程控制中的应用研究。

