基于置信规则和证据推理的超声检测缺陷识别
王 力, 周志杰,2, 胡昌华, 刘涛源
(1.火箭军工程大学控制科学与工程系,陕西 西安 710025;2.西安理工大学自动化与信息工程学院,陕西 西安 710048)
基于置信规则和证据推理的超声检测缺陷识别
王 力1, 周志杰1,2, 胡昌华1, 刘涛源1
(1.火箭军工程大学控制科学与工程系,陕西 西安 710025;2.西安理工大学自动化与信息工程学院,陕西 西安 710048)
为解决超声检测缺陷精确识别问题,综合运用检测数据和专家知识,研究一种基于置信规则库(belief-rulebase,BRB)和证据推理(evidential reasoning,ER)进行超声检测缺陷识别的方法。提出一种融合多种特征信息的BRB-ER缺陷识别模型,利用最小均方误差算法进行模型初始参数的优化,从而提高缺陷识别的准确性。通过超声检测手段获取某航空材料的缺陷数据,并对所提出识别方法进行验证。试验结果显示:该方法能够准确地进行缺陷识别,并可根据已有的产品缺陷类型进行训练,建立更加准确的缺陷识别模型。
置信规则库;证据理论;模式识别;超声检测
0 引 言
随着科学技术的不断发展,无损检测技术现已广泛应用于产品质量、设备维护等安全检测方面。其中,超声检测技术因其具有被检测对象范围广、检测深度大、缺陷定位准确、检测灵敏度高等特点,应用最为广泛,使用频率最高[1]。
对缺陷进行定量和定性分析是超声检测的关键内容。由于检测原理和方法、检测设备和系统、材料等各种因素的影响,难以仅仅根据检测信号的定量信息对缺陷进行精准识别,通常只能给出可能包含有(不包含有)某种缺陷的可能性大小的结论。然而,实际工程应用中往往需要给出的缺陷形状、种类等定性结论,很大程度上依赖于检测人员的专业知识、技术水平和工作经验等主观因素[2]。
因此,在超声检测缺陷识别中,为了综合利用带有不确定性的检测系统的定量信息与检测人员的定性知识,引入数据融合方法对定量信息和定性知识进行有效处理是很有必要的[3]。传统的数据融合方法,主要通过贝叶斯等统计学方法进行融合,但无法有效处理不确定性信息。另外,基于概率理论的贝叶斯方法主要侧重于处理定量信息,需要大量的历史数据确定先验分布等参数,但无法较好地使用定性知识[4]。因此,Yang等[5-6]提出了基于证据推理算法的置信规则库推理方法,它是在D-S证据理论、决策理论、模糊理论和传统IF-THEN规则库的基础上发展起来的,具有对带有模糊不确定性、概率不确定性以及非线性特征的数据建模能力。
为了在超声缺陷识别中有效利用检测信号的定量信息和检测专家的定性知识,本文提出了一种基于置信规则库和证据推理的缺陷识别方法。首先,提出了一种融合多种特征信息BRB-ER缺陷识别方法。其次,对已建立方法模型的初始参数进行优化,从而提高缺陷识别的准确率。最后,通过超声检测手段获取某航空材料的缺陷数据,并对提出的方法进行了验证。
1 BRB-ER缺陷识别方法
1.1 BRB-ER结构模型
构建的BRB-ER缺陷识别模型结构如图1所示。BRB-ER缺陷识别方法主要包含两个部分:第1部分是BRB,主要进行缺陷识别规则的建立;第2部分是ER,主要进行规则的推理合成。当通过超声检测的手段获取原始数据,经过预处理和小波包变换提取数学特征后所获得的特征信息,就可以利用该BRB-ER模型进行推理和融合,最后得到缺陷识别的结果。

图1 BRB-ER缺陷识别模型结构
1.2 BRB专家系统
为了对缺陷模式进行识别,运用专家知识构造了一系列置信规则,并构建了置信规则库[7]。其中,第K条规则描述如下:
Ai(i=1,…,M)——第i个前提属性的参考值;
M——前提属性的个数;
Di(i=1,…,N)——根据规则得到的评估结果;
θk(k=1,…,K)——第K条规则的规则权重,它反映了第K条规则相对于BRB中其他规则的重要度;
δi(i=1,…,M)——在第i个前提属性的权重,它反映了第i个前提属性相对于其他前提属性的重要度;
βj,k(j=1,…,N;k=1,…,K)——在第K条规则中相对于输出部分的 (即置信规则的Then部分)第j个评估结果的Dj置信度;
∧——“AND”的简写,逻辑“与”的关系。
对于BRB的参数,它们需要满足以下约束条件:
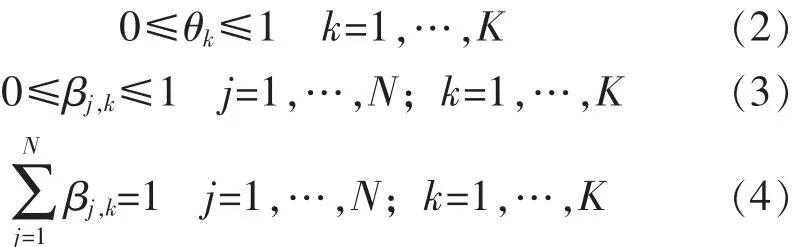
在超声检测过程中,对超声检测信号进行数据预处理和小波包分解法的特征提取后获得特征数据,主要包括以下6个时域特征指标:斜度、峰度、峰值指标、清除指标、形状指标、脉冲指标[8]。考虑以下数据集:

在缺陷识别中,假设总共有4种识别结果,分别是缺孔、裂纹、夹渣、凹坑。那么识别结果可以表示为
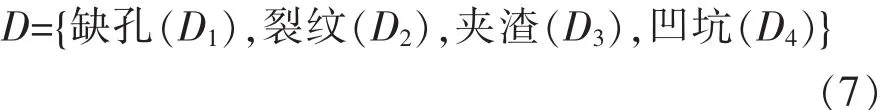
如果该组数据的识别结果为缺孔(D1),那么缺孔(D1)的置信度为 1,而裂纹(D2)、夹渣(D3)、凹坑(D4)的置信度都为0。置信度分配可表示为:β=(1,0,0,0)。
结合识别结果,可以表示为
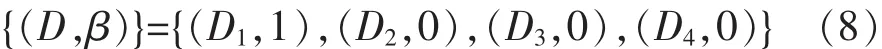
综上所述,BRB中第K条规则表示如下:

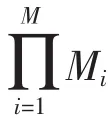
1.3 BRB推理
根据Chang所提出的方法,BRB中的规则推理分为两步,第1步是计算第K条规则的激活权重,第2步是根据激活权重对各个规则进行融合。
1.3.1 BRB推理定义
根据Chang所提出的方法,在建立规则时可以最少只保留3条规则,其中两条属性值中最大值、最小值组合作为边界。也可以根据实际增加规则条数,以提高建模精度。其激活权重计算方法如下:
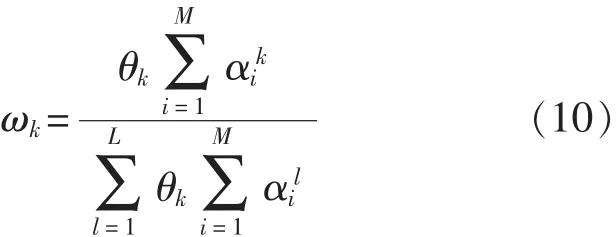
式中:θk——第k条规则的相对权重;
αik——输入信息与第K条规则中第i个前提属性的匹配度,i∈(1,M),k∈(1,L)。
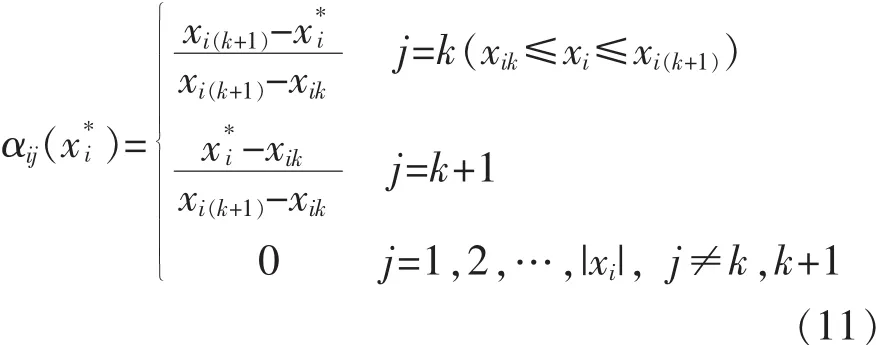
xi(k+1)、——第i个前提属性相邻状态的参考值。
1.3.2 证据推理
当BRB中第K条规则被激活后,使用ER算法用来对置信规则库中的规则进行组合,可以得到BRB最终的输出 S(x)。
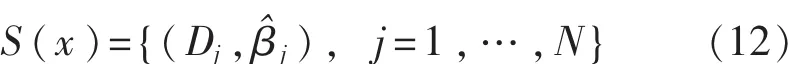
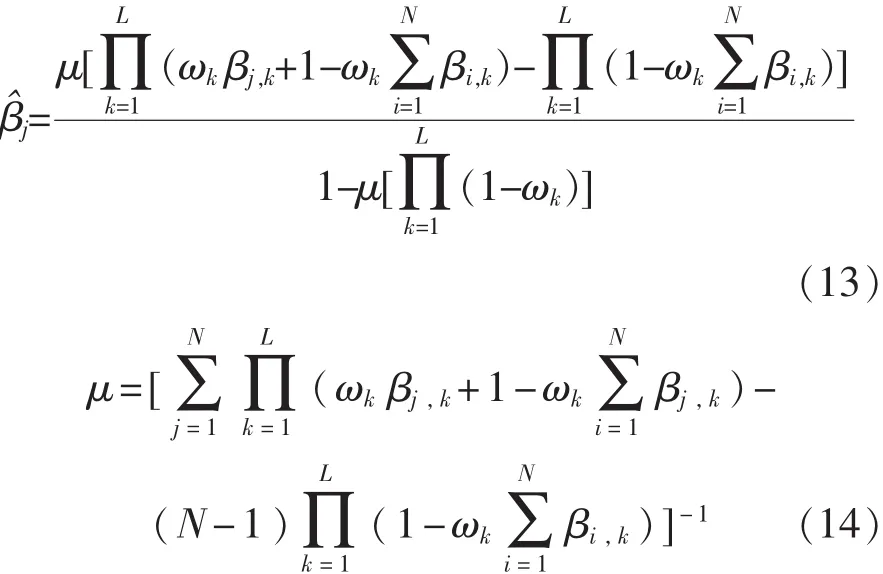
BRB在建立初始规则时,模型的参数是由专家给定的,这可能导致系统不能完全适应缺陷识别的要求,其识别的精度可能会降低。因此,本文提出了一种BRB-ER模型参数优化算法,来对模型的初始参数进行优化,从而提高缺陷识别的精度。
2 一种BRB-ER模型优化算法
在 BRB 模型中存在的初始参数 θk、β赞j,通常根据专家知识给定。但是当BRB系统比较复杂时,专家难以确定这些参数的精确值,所提供的参数值也不能完全适应缺陷精确识别的要求。因此,需要建立模型优化训练算法,对初始参数进行优化训练。对于BRB-ER模型,需要优化的参数包括:
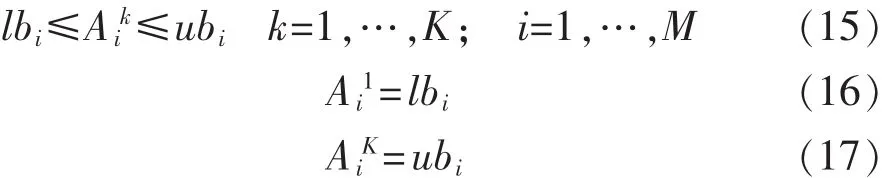
其中lbi和ubi分别为第i个属性的下界和上界。
2)初始规则权重。对第k条规则,其初始权重θk,必须满足如下约束:

3)每条规则结论部分的置信度。对于第i条规则,其结论部分置信度βn,k,必须满足如下约束:
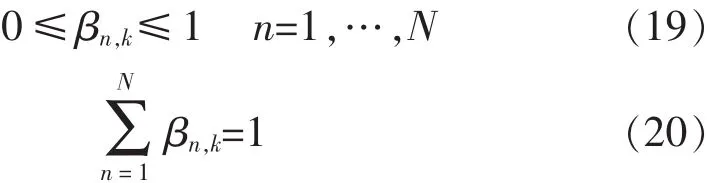
其次,优化目标为估计输出与实际输出的差值,并且应使误差尽可能小。可知,由BRB推理得出的估算向量与输入向量具有相同的置信结构,选择识别结果中置信度数值最大的作为最终的识别结果。假设T表示缺陷模式的实际结果,T′表示缺陷模式的识别结果,则 ΔT(Q)=T-T′表示实际结果T和识别结果 T′的误差,Q 表示参数 θk、、ωk的集合。
因此,实际结果与识别结果之间的均方误差(MSE)应为
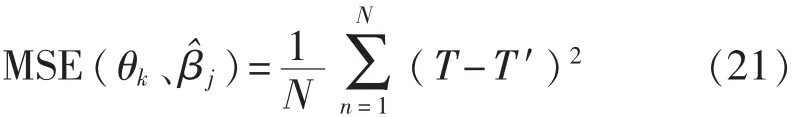
图2显示了参数训练的过程。其中,t1,…,tm表示不同缺陷的特征数据。
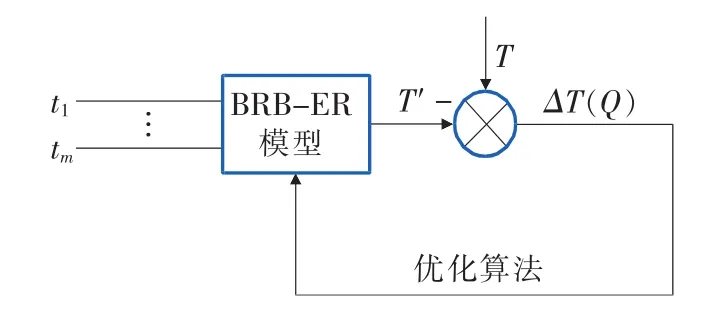
图2 BRB-ER模型参数训练的优化算法
当MSE越小时,模型参数越准确、合理。仅仅靠专家的知识经验构造该模型很难使模型参数达到最优结果。因此,构造了下面的非线性模型,用于训练模型参数:
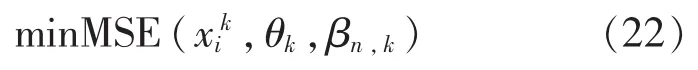
在优化过程中,首先给定初始参数,根据优化模型,利用训练数据对模型进行训练。优化方法可以采用智能优化算法,如遗传算法、模拟退火算法、差分进化算法等,也可以利用Matlab优化工具箱来优化模型参数,本文通过Matlab工具箱中的非线性优化函数fmincon和fminsearch求解参数最优值。
3 应用研究
为了验证本文所提出的基于BRB-ER模型进行缺陷识别方法的有效性,利用超声检测手段对某航空材料进行检测,根据所提出的模型进行缺陷识别。
3.1 问题描述
为了有效表达不同类型的超声检测信号的特征,一般从信号的数学特征和变换特征方面对超声检测信号进行特征提取。本文采用信号数学特征,主要从时域中选取峰度、斜度、峰值指标、清除指标、形状指标、脉冲指标共6个无量纲参数作为缺陷识别属性信息,试图反映出损伤类型的本质特征。首先定义采样信号的均值和标准偏差。
假设采样的信号为 S,其采样点为 si(i=1,2,…,N),采样个数为N,则信号的均值s¯为

样本标准偏差s为
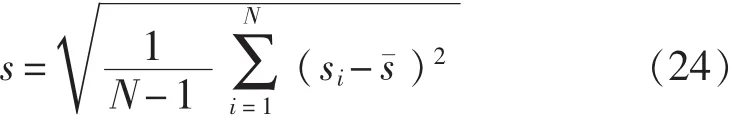
从时域中选取以下6个无量纲参数作为缺陷识别属性信息:
斜度:
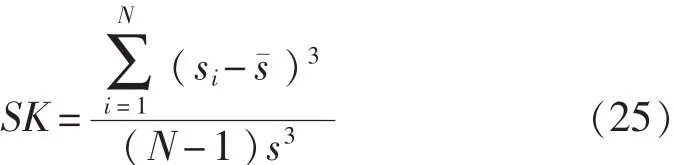
峰度:
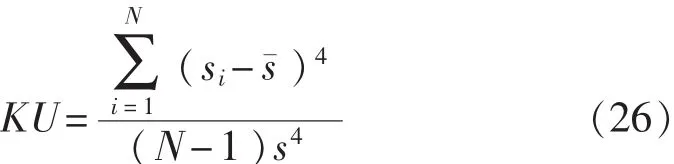
峰值指标:

清除指标:
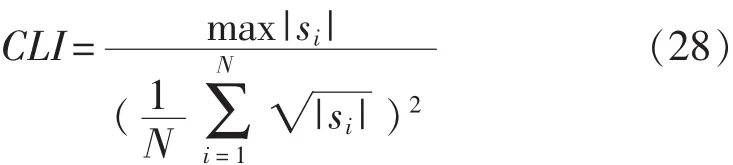
形状指标:
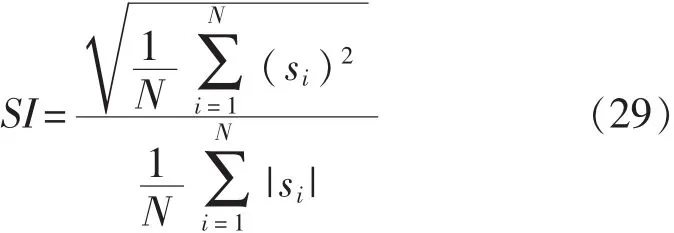
脉冲指标:
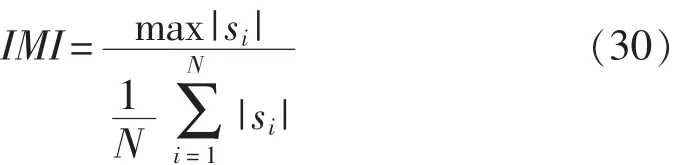
总共有4种缺陷识别的结果,分别为:缺孔、裂纹、夹渣、凹坑。共计算得属性信息100组数据,其中部分数据如表1所示。
本文随机选择测得数据中的80组作为训练数据,对模型参数进行优化训练。用剩余20组数据进行测试检验优化后模型的有效性。
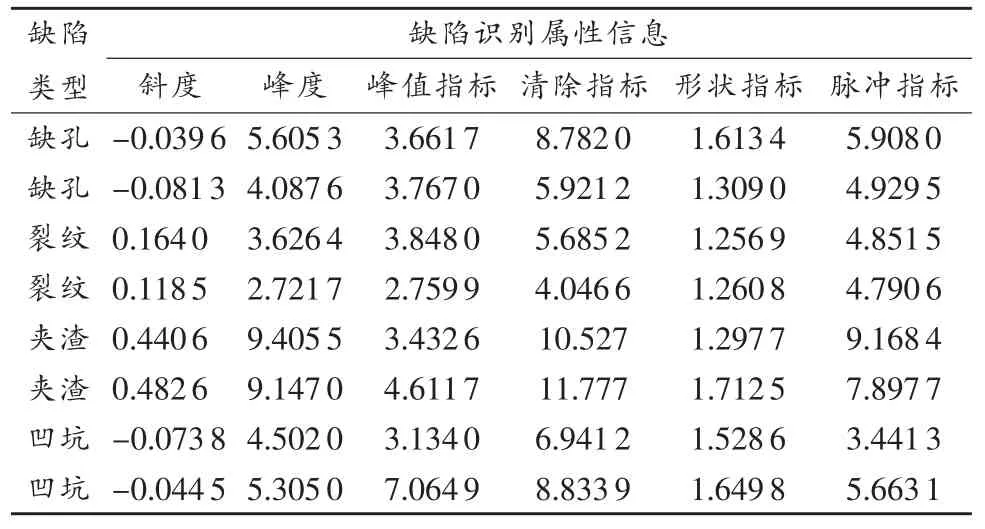
表1 缺陷识别属性边界数据
3.2 BRB-ER缺陷识别模型建立
假设:
{A1,A2,A3,A4,A5,A6}={斜度,峰度,峰值指标,清除指标,形状指标,脉冲指标}
D={缺孔(D1),裂纹(D2),夹渣(D3),凹坑(D4)}
本文利用Chang[9]所提出的一种新的规则激活和权重激活的计算方法,构造简化的BRB规则。根据检测的数据,可得缺陷模式识别每个前提属性的参考值的最大值和最小值。假设每个前提属性均有3个参考值,分别为最大值、最小值和中位数,构造简化的BRB规则如下:

初始置信度的确定主要依靠定性知识,规则权重统一设为1。各组数据权重的初始值由专家给定,详细的初始置信度确定方法已经由Xu等[10]提出。
3.3 BRB-ER缺陷识别模型训练优化
构造BRB-ER模型后,可以对缺陷模式进行识别。为了验证优化后的模型能够更加准确的对缺陷模式进行识别,选取测得数据中的80组作为训练数据,利用Matlab工具箱的优化函数对模型参数进行优化训练,得到优化后BRB规则的权重和置信度如表2所示。
3.4 模型识别结果与分析
根据以上优化参数,能够构造准确率较高的BRB-ER缺陷识别模型。利用剩余20组数据对优化后模型的有效性测试检验,结果如表3所示。由表可知,利用20组数据进行BRB-ER缺陷识别的检验中,共有18组数据的缺陷模式能够被正确识别,成功识别率为90%。
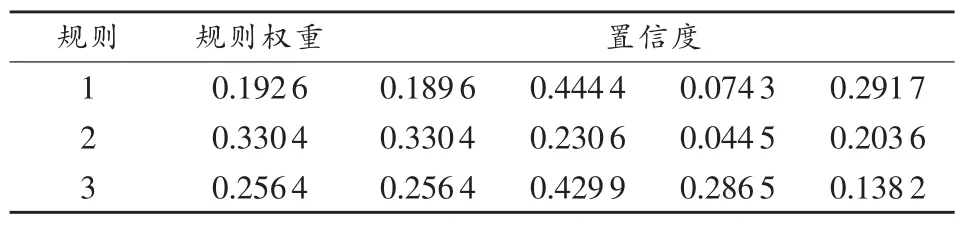
表2 参数优化后得到的权重和置信度
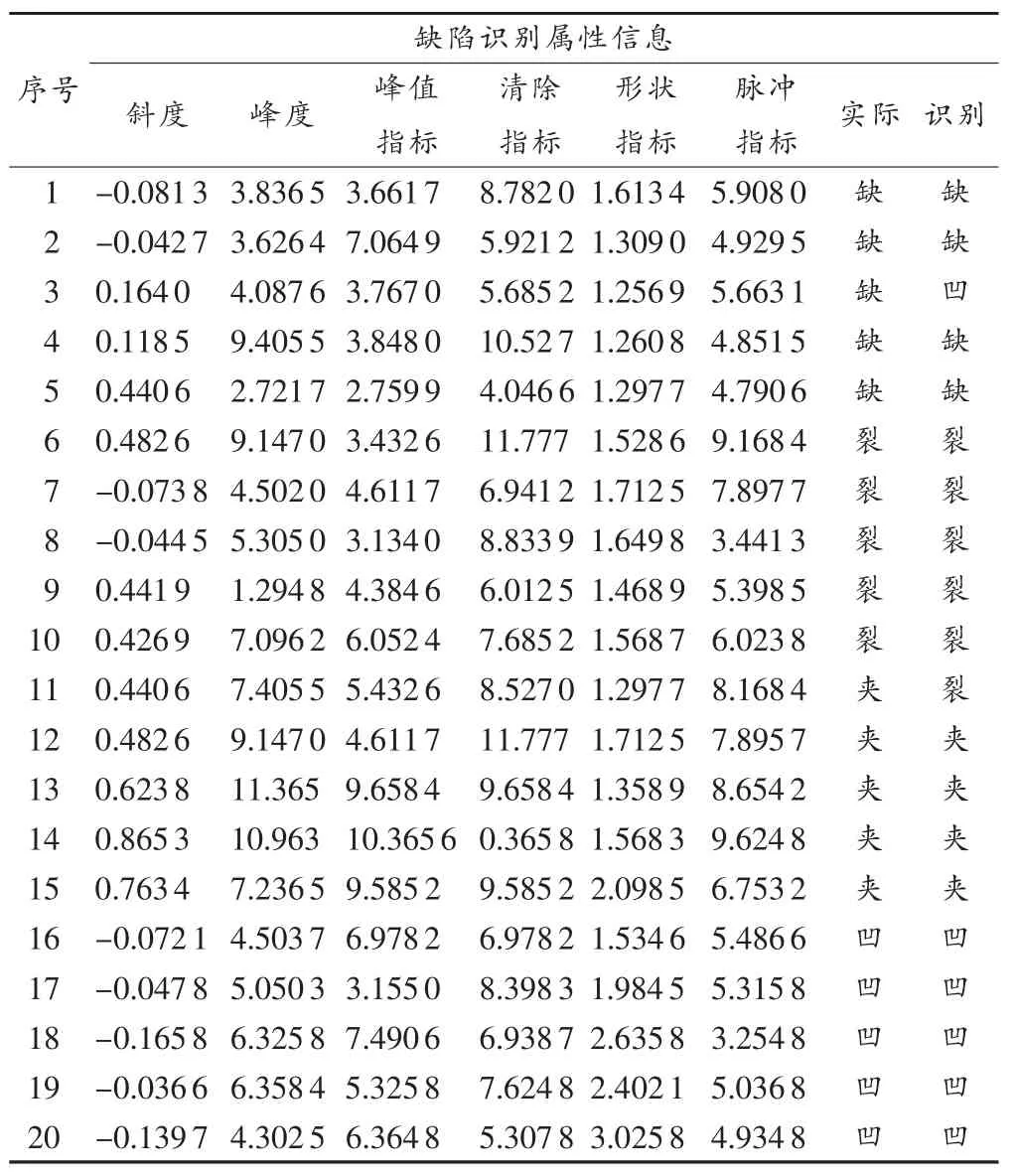
表3 超声缺陷识别测试检验1)
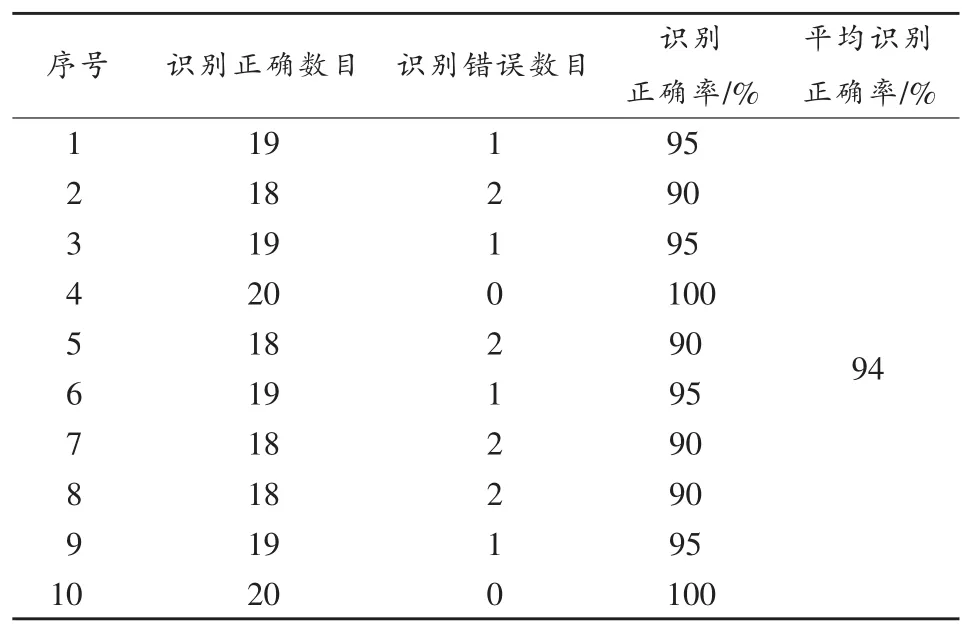
表4 随机测试验证结果
本文总共做了10组随机测试,即每次随机抽取80组数据建立模型,利用剩余20组进行模型验证,得到的实验结果如表4所示。可以看出,本文所用模型具有较好的稳定性,10次测试的平均识别准确率为94%。
4 结束语
本文研究了一种基于置信规则和证据推理进行缺陷识别的方法。综合利用超声检测系统获得航空材料属性信息和专家知识给出的模型初始参数,建立规则置信库,利用证据推理对缺陷模式进行分类识别。首先,提出了一种融合多种特征信息BRB-ER缺陷识别方法。其次,对已建立模型的初始参数进行优化,从而提高识别的准确性。最后,根据某航空材料的缺陷数据对该方法的有效性进行验证。
研究结果表明,该方法能够有效利用缺陷信号的定量信息和专家经验的定性知识,建立更加优化的缺陷识别模型,从而提高缺陷识别的准确率。但是在建立模型时,需要根据专家知识给出模型的初始参数,当属性信息较多时专家知识不一定非常准确,可能会影响到缺陷识别的准确性,这也是下一阶段的研究重点。
[1]美国无损检测学会.美国无损检测手册(超声卷)[M].北京:世界图书出版社,1996:28-38.
[2]张道富,曾燕,周晓车,等.基于信息融合技术的无损检测缺陷模式识别[J].仪器仪表学报,2003,24(5):449-452.
[3]韩崇朝,朱红艳,段战胜,等.多源信息融合[M].北京:清华大学出版社,2006:19-44.
[4]潘泉,王增福,梁彦,等.信息融合理论的基本方法与进展(II)[J].控制理论与应用,2012,29(10):1233-1234.
[5]YANG J B.Rule and utility based evidential reasoning approach formulti-attribute decision analysisunder uncertainties[J].European Journal of Operational Research,2001,131(1):31-61.
[6]YANG J B, LIU J, WANG J.Belief rule-base inference methotology using the evidential reasoning approach-RIMER[J].Systems, Man and Cybernetics(Part A),2006,36(2):266-285.
[7]周志杰,杨剑波,胡昌华,等.置信规则库专家系统与复杂系统建模[M].北京:科学出版社,2011:9-30.
[8]叶钱.噪声背景下金属材料小缺陷超声检测关键技术的研究[D].杭州:浙江大学,2015.
[9]CHANG L L, ZHOU Z J, YOU Y, et al.Belief rule based expert system for classification problems with new rule activation and weightcalculation procedures[J].Information Science,2016,336(1):75-91.
[10]XU D L, LIU J, YANG J B, et al.Inference and learning methodology of belief-rule-based expert system for pipeline leak detection[J].Expert Systems with Applications,2007,32(1):103-113.
(编辑:李刚)
Ultrasonic testing defect recognition based on belief-rule-base and evidential reasoning
WANG Li1,ZHOU Zhijie1,2,HU Changhua1,LIU Taoyuan1
(1.Department of Control Engineering,Rocket Force University of Engineering,Xi’an 710025,China;2.School of Automation and Information Engineering,Xi’an University of Technology,Xi’an 710048,China)
To improve accuracy in defects recognition by ultrasonic testing,a method of defects recognition based on belief-rule-base(BRB)and evidential reasoning(ER)is proposed according to test data and expert knowledge.Firstly,a new model of defects recognition integrating feature information based on belief-rule-base(BRB) and evidential reasoning(ER) is presented,and then the initial parameters of model are optimized with the minimum mean square error algorithm to improve the accuracy of defects recognition.Finally,ultrasonic testing is used to get the defect data of one aeronautical material and a case study is carried out to illustrate the ability and efficiency of the proposed method.The study results show that the method can recognize defects accurately.A more accurate defects recognition model is established based on exercises on existing product defects.
belief-rule-base;evidential reasoning;pattern recognition;ultrasonic testing
A
1674-5124(2017)04-0006-05
10.11857/j.issn.1674-5124.2017.04.002
2016-09-19;
2016-11-23
国家自然科学基金(61370031,60736026);飞行器海上测量与控制联合实验室开放基金(FOM2014OF14)
王 力(1992-),男,陕西西安市人,硕士研究生,专业方向为诊断技术及自动化装置。

