自动化集装箱码头自动导引小车与轨道式龙门起重机的协同调度

杨勇生+冯有勇+梁承姬+许波桅+李军军

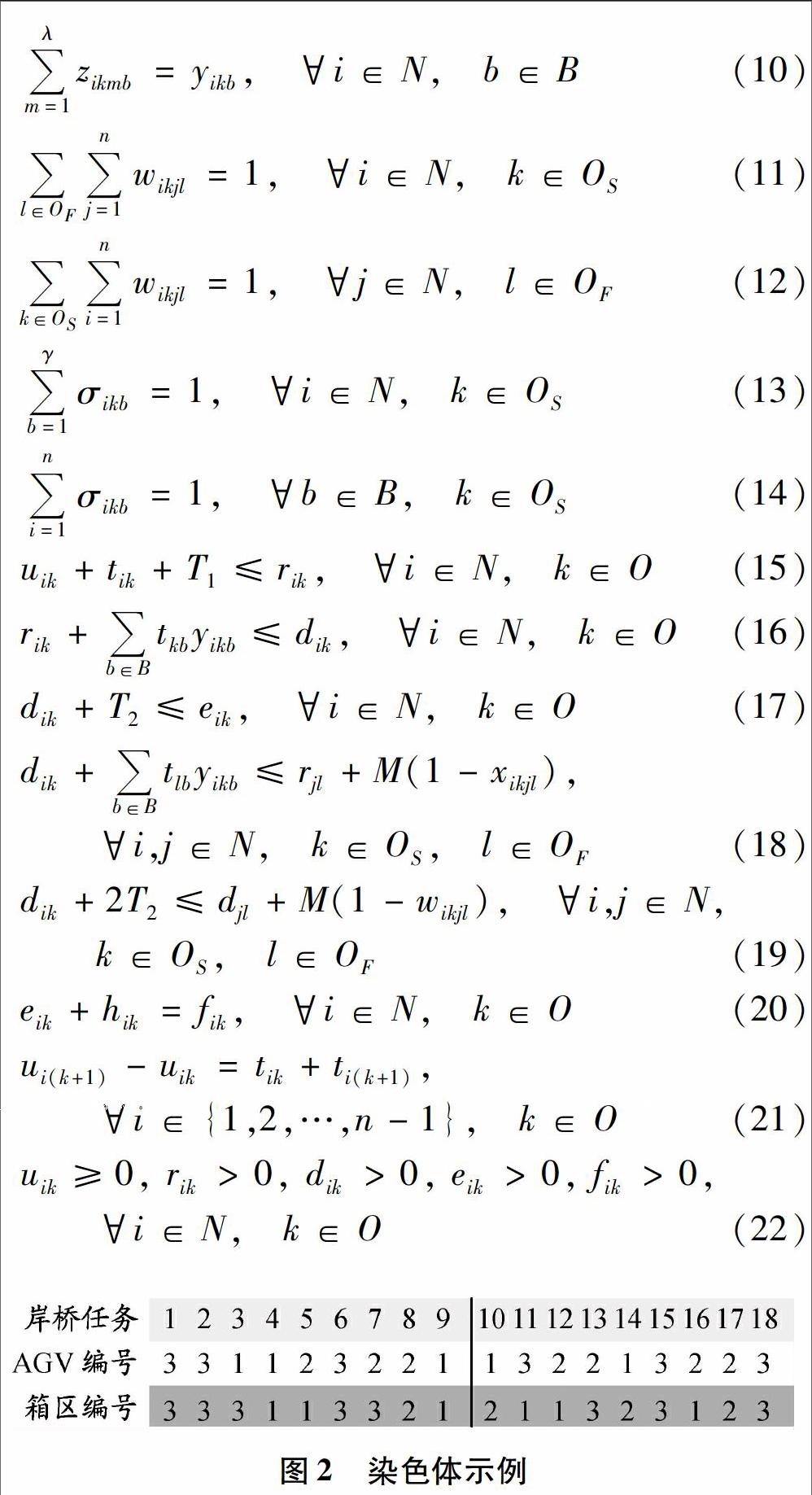
摘要：为解决自动导引小车（Automated Guided Vehicle，AGV）与轨道式龙门起重机（RailMounted Gantry Crane， RMG）的协同调度问题，考虑AGV和RMG的任务分配约束，以卸船作业最小完工时间为目标，建立混合整数规划（Mixed Integer Programming， MIP）模型.改变AGV，岸桥和箱区数量的配置，得出不同条件下的完工时间.对该问题设计两组算例：小规模算例采用CPLEX软件和遗传算法（Genetic Algorithm，GA）分别进行求解，通过结果对比验证GA的有效性；大规模算例采用GA求解，给出自动化码头设备调度优化方案.分析结果表明，卸船完工时间随着卸船任务量的增加而增加，随着AGV，岸桥和箱区数量的增加而减少，且AGV和岸桥数量的增加对完工时间的影响大于箱区数量的增加时完工数量的影响.

关键词： 自动导引小车（AGV）； 堆场箱区； 协同调度； 混合整数规划（MIP）； 遗传算法（GA）

中图分类号： U656.135； U691.34

文献标志码： A

Abstract： For the integrated scheduling issue of Automated Guided Vehicles （AGVs） and RailMounted Gantry Cranes （RMGs）， a Mixed Integer Programming （MIP） model is proposed so as to minimize the makespan of unloading operation with task allocation constraints of AGVs and RMGs. Changing the numbers of AGVs， quay cranes and blocks， the makespans under different conditions are obtained. Two groups of examples are performed. The smallsized examples are solved by CPLEX software and Genetic Algorithm （GA） respectively， and the validity of GA is verified by comparing the results. The largesized examples are solved only using GA， and the equipment scheduling scheme at an automated container terminal is given. The results show that the makespan increases with the increase of unloading task， and decreases with the increase of the numbers of AGVs， quay cranes and blocks， where the effects of the increase of the numbers of AGVs and quay cranes on the makespan are greater than that of the increase of the number of blocks.

Key words： Automated Guided Vehicle （AGV）； block； integrated scheduling； Mixed Integer Programming （MIP）； Genetic Algorithm （GA）

0 引 言

由于勞动力成本上升、船舶大型化和码头作业高效化等多重原因的影响，国内外已经掀起了自动化集装箱码头（简称自动化码头）研究的热潮.近年来，自动化码头成为中国各港口重点建设对象，如：厦门远海自动化码头已建成，目前处于调试阶段；上海洋山四期自动化码头正在建设中. 自动导引小车（Automated Guided Vehicle，AGV）是一种典型的水平运输设备，装备有电磁、激光等自动导引装置，沿着规定的导引路径在岸桥与堆场间来回作业，完成集装箱装卸任务.本文针对卸船作业过程，研究AGV与轨道式龙门起重机（RailMounted Gantry Crane，RMG）的协同调度问题.

目前，国内外学者对自动化码头AGV调度已有一定的研究.单独研究AGV调度的有：CHOE等[1]以AGV空驶距离最短和岸桥作业时间最短为优化目标，提出一种基于人工神经网络的在线学习算法，实时选择最优的AGV调度方案；KIM等[2]以任务的总延迟时间和AGV 的总运输成本最小为优化目标，采用整数规划模型对自动化码头AGV的静态调度问题进行了研究；ANGELOUDIS等[3]对不确定环境下自动化码头AGV任务分配问题提出了一种滚动时域的策略，最大限度地减少船舶的在港时间，提高自动化码头的作业效率；MIYAMOTO等[4]主要考虑AGV在自由路径上的调度，考虑缓冲区的容量限制，提出了本地搜索和随机搜索的方法并进行评估；邱跃龙等[5]在分析自动化码头AGV工作的基础上，建立了基于Petri网的AGV运输路径模型，并对其进行了系统性能分析；马越汇等[6]为研究不确定环境下自动化码头AGV 调度与配置问题，建立了以最小化最末任务结束时间为目标的基本模型，并通过算例证明了模型的有效性和实用性；霍凯歌等[7]研究了自动化码头多载AGV调度问题，以最小化作业费用为目标，建立了混合整数规划模型，通过Gurobi和遗传算法（Genetic Algorithm， GA）求解；康志敏[8]提出在作业面调度模式下，考虑集装箱装卸并行的作业工艺，建立以等待时间最少为目标的AGV调度模型，并利用GA进行求解；柯冉绚等[9]为解决集装箱码头AGV调度优化问题，建立以无效时间最短为原则的数学模型，采用

NetLogo软件进行仿真，比较了“作业线”与“作业面”两种AGV调度模式.

相比单独研究AGV调度，研究AGV与场桥或岸桥集成调度的很少，其中最具代表的有：MEERSMANS等[10]最早提出解决自动化码头AGV，岸桥和场桥集成调度问题，采用分支定界和定向搜索方法在合理的时间内求出最小完工时间；WU等[11]和LUO等[12]采用GA研究岸桥与AGV的集成调度，考虑边装边卸和只卸不装两种作业模式，有效减少了船舶在港时间；XIN等[13]提出一种方法论，在提高自动化码头作业效率的同时减少AGV，岸桥和自动堆垛机的能源消耗，通过仿真论证了该方法的有效性.

传统码头与垂岸式自动化码头布局的不同使集卡与AGV的调度方式有着很大的差别：AGV行驶路径比较固定，而集卡调度路径相对比较灵活，可根据实时道路交通状况改变路径.随着AGV数量的增加，AGV之间发生死锁与冲突的概率变大，给AGV调度带来很大的难度，并且随着装卸设备的改进，岸桥和场桥的结构发生了显著变化.因此，研究新的装卸设备具有重要的实用价值.本文主要考虑的是双小车岸边起重机、AGV和接力式双轨道龙门起重机等3种自动化码头设备的调度问题.

1 问题描述

垂岸式自动化码头包含泊位区、岸桥作业区、堆场箱区、AGV水平运输区等区域，其布局见图1.

本文采用的岸桥是双小车岸边起重机.与传统岸桥不同，双小车岸边起重机有2台小车，一般将靠近海侧的称为海侧小车，另一台称为岸侧小车.岸桥采用接力式的作业方式，海侧小车将集装箱从船卸至中转平台，随即岸侧小车将中转平台上的集装箱卸至AGV.由于海侧小车不用等待AGV，可以连续进行卸船作业，因此这种卸箱工艺能最大程度地减少船舶在港时间.本文采用的场桥是接力式双轨道龙门起重机，每个箱区配置2台，分别记为RMG1和RMG2.两台RMG互相合作完成任务作业，具体流程为：首先AGV通过水平运输将集装箱运输到堆场交接区，接着RMG1将集装箱从AGV上卸下，放到箱区的暂存区；接着AGV回到岸桥的交接区运输下一个集装箱，与此同时，RMG2将暂存区的集装箱卸到指定位置，直到完成所有的卸箱任务.本文主要针对进口箱作业，已知岸桥卸箱作业顺序，结合岸桥、AGV和RMG等3种设备，建立以最小化最末卸箱任务结束时间为目标的混合整数规划模型，采用CPLEX软件和GA进行求解，并给出相应的调度方案.

2 模型建立

2.1 模型假设

根据自动化码头的实际情况，对问题进行合理的简化.在实际卸船过程中，海侧小车、AGV和RMG2的运行时间与集装箱初始位置（船上位置）和最终位置（箱区位置）有关，因此可以假设其运行时间在一个范围内.[14]

假设：（1）提前分配岸桥给集装箱船，且已知岸桥卸箱作业顺序；（2）海侧小车取箱至中转平台的时间在一个范围内；（3）岸侧小车取箱时间不计，且从中转平台取箱放到AGV上的时间已知；（4）AGV从岸桥交接区行驶至堆场交接区的时间在一个范围内；（5）RMG1取箱时间不计，且取箱至暂存区的时间已知；（6）RMG2取箱时间不计，且将集装箱放至指定位置的时间在一个范围内；（7）当AGV开始下一个卸箱作业时，若没有可用岸桥和RMG，则AGV需要等待，同理，若岸桥和RMG没有可用的AGV，则岸桥和RMG也要等待；（8）AGV可以服务任何一个岸桥，集装箱可以堆存到任何一个箱区.

2.2 模型参数

称每卸载1个集装箱为岸桥完成1个任务.N为任务集合，N={1，2，…，n}，i，j∈N；K为所有岸桥的集合；B为所有可用箱区的集合，b∈B；S为虚拟开始岸桥；F为虚拟结束岸桥；V为所有可用AGV的集合， v∈V；OS=K∪{S}，OF=K∪{F}，O=K∪{S，F}；k，l∈O；φ为可用AGV的总数；γ为可用箱区的总数；λ为分配给箱区b的任务数；uik为岸桥k开始执行第i个任务的时刻；tik为海侧小车将船上的集装箱卸到中转平台上所需的时间；T1为岸侧小车将中转平台上的集装箱卸到AGV上花费的时间；rik为AGV执行岸桥k的第i个任务的时刻；tkb为AGV从岸桥k运行到箱区b交接区所需要的时间；dik为AGV到达箱区交接区的时刻；T2为RMG1将集装箱卸到暂存区所需时间；eik为RMG2开始执行岸桥k的第i个任务的时刻；hik为RMG2将岸桥k的第i个集装箱运到指定位置所需的时间；fik为完成岸桥k的第i个任务的时刻；M是一个较大的整数.

决策变量：xikjl∈{0，1}，xikjl=1表示AGV完成岸桥k的第i个任务后接着执行岸桥l的第j个任务，否则xikjl=0；βikv∈{0，1}，βikv=1表示岸桥k的第i个任务分配给编号为v的AGV，否则βikv=0；zikmb∈{0，1}，zikmb=1表示岸桥k的第i个任务是箱区b的第m个任务，否则zikmb=0；yikb∈{0，1}，yikb=1表示岸桥k的第i个任务落在箱区b上，否则yikb=0；wikjl∈{0，1}，wikjl=1表示RMG完成岸桥k的第i个任务后再去执行岸桥l的第j个任务，否则wikjl=0；σikb∈{0，1}，σikb=1表示岸桥k的第i个任务分配给编号为b的箱区，否则σikb=0.

基本模型是一個混合整数规划模型[12].令岸桥卸第1个集装箱的时刻为0，即u1k=0，k∈O.式（1）表示最小化卸船任务的完工时间；式（2）表示岸桥k完成所有任务的时刻（Fk）与完成每个任务的时刻的关系；式（3）表示岸桥k开始执行任务的时刻（Sk）与每个任务开始的时刻的关系；式（4）表示AGV完成1个集装箱运输任务后还有1个集装箱运输任务；式（5）表示AGV开始集装箱运输任务之前有1个集装箱运输任务；式（6）表示每个集装箱运输任务只能由1辆AGV完成；式（7）表示每辆AGV每次只能完成1个集装箱运输任务；式（8）表示每个待卸集装箱都会堆存在堆场箱区；式（9）表示每个箱区至少会有1个卸箱任务；式（10）构建了1个中间变量用来表示2个决策变量之间的关系；式（11）表示RMG完成1个卸箱任务后还有1个卸箱任务；式（12）表示RMG开始执行卸箱任务前有1个卸箱任务；式（13）表示每个集装箱只能堆存在1个箱区上；式（14）表示

RMG每次只能完成1個卸箱任务（RMG每次只能卸1个集装箱）；式（15）表示在岸侧将集装箱放到AGV上后，AGV才能开始执行任务；式（16）表示AGV到达堆场交接区的时刻与RMG1开始作业时刻的关系；式（17）表示RMG1将集装箱运到暂存区的时刻与RMG2开始作业时刻的关系；式（18）表示当AGV完成上一个集装箱运输任务再回到下一个集装箱运输任务指定岸桥缓存区后，才能开始执行下一个任务；式（19）表示RMG1的下一个卸箱任务开始时刻与上一个卸箱任务开始时刻的关系；式（20）表示完成任务的时刻；式（21）表示岸桥执行两个相邻任务的开始时刻关系；式（22）表示时间参数的范围.

3 GA求解

本文所提出的问题涉及岸桥、AGV和RMG，因此采用多层染色体及整数编码的方式表示自动化码头调度问题.假设有2台岸桥，每台岸桥有9个卸箱任务，1～9为岸桥1的任务，10～18为岸桥2的任务，采用3辆AGV进行水平运输，将集装箱随机卸到3个箱区.第i个卸箱任务的编码v，b表示第v辆AGV将1个集装箱运送到箱区b.染色体示例如图2所示.根据箱区对染色体进行解码，即将分配给不同箱区的集装箱进行适应度值的计算，然后对适应度值进行比较，最大的适应度值即为所求目标函数.

由于每个卸箱任务可以被任何1辆AGV和任何1台RMG服务，为提高计算最优解的效率，交叉操作采用两点交叉原则（即只需要对染色体的AGV编号和箱区编号进行交叉操作），变异操作是针对单条染色体进行的（即只要对染色体中AGV编号和箱区编号进行变异操作）.

交叉操作的具体做法为：选择2条父代染色体，随机产生2个切点位置，交换2个切点位置的AGV编号和箱区编号，得到子代染色体.变异操作的具体做法为：随机选择1条父代染色体，确定其中2个变异点，交换2个变异点相对应的子串，得到子代染色体.

4 算例分析

首先对参数进行初步设定.对小规模问题（卸箱任务较少），采用MATLAB中的YALMIP工具箱结合CPLEX 12.2求解器进行精确求解，同时采用GA进行近似求解，通过对两种结果进行对比来验证GA的有效性.随着问题规模的扩大，即卸箱数量增加，很难采用精确求解方法解决问题，故采用GA获得满意解.

4.1 参数设定

卸箱数量为4～200个，4～20个集装箱卸载任务视为小规模问题，21～200个集装箱卸载任务视为大规模问题，AGV数量为3～10辆，箱区数量为2～7个，岸桥数量为2～5台.海侧小车处理集装箱的时间服从均匀分布U（30 s，70 s）；RMG2处理集装箱的时间服从均匀分布U（80 s，140 s）；AGV行驶时间（从岸桥交接区到堆场交接区的时间）服从均匀分布U（20 s，90 s）；岸侧小车和RMG1处理集装箱时间是确定的，分别为20 s和25 s.GA参数设置：交叉概率Pc=0.8，变异概率Pm=0.05，初始种群为50，最大迭代次数为200.

4.2 小规模算例

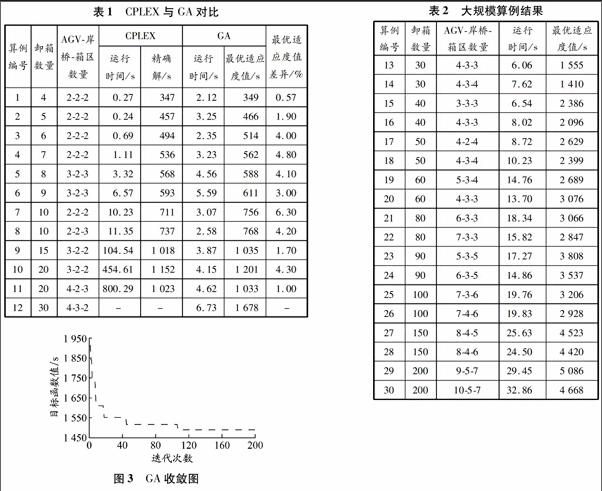
小规模问题集装箱任务为4～20个，分别采用CPLEX和GA进行求解.由于GA求解结果存在随机误差，所以为减小这个随机误差，每个算例运行20次，记录其平均运算时间和平均最优适应度值.最优适应度值差异表示采用GA求得的最优适应度值与采用CPLEX得到的精确解之间的差异程度.详细的计算结果见表1.

以算例5为例，共有8个集装箱任务，3辆AGV，2台岸桥和3个箱区.利用CPLEX可得到AGV最优调度方案：AGV1的调度方案为（1，1）→1，（1，3）→1，（2，2）→2；AGV2的调度方案为（2，1）→2，（2，3）→1，（1，4）→2；AGV3的调度方案为（1，2）→1，（2，4）→2.也就是说，AGV1执行岸桥1的第1个任务到达箱区1，执行岸桥1的第3个任务到达箱区1，执行岸桥2的第2个任务到达箱区2.同理可得AGV2和AGV3的具体调度方案.利用CPLEX求解该算例的运行时间为3.32 s，精确解为568 s.

从算例1～3可知，当卸箱数量较小时，CPLEX能很快计算出结果.然而，随着卸箱数量的增加（如算例9和10），CPLEX的求解时间越来越长，当卸箱数量达到30个时，CPLEX无法在可接受的时间内得到精确解.从算例7和8可知，当卸箱数量相同时，箱区数量增加使CPLEX的求解时间变长.再观察GA的性能：随着卸箱数量的增加，GA的求解时间并没有随着卸箱数量的增加而剧烈变化，几乎稳定在2～7 s之间；利用GA求得的最优适应度值与利用CPLEX求得的精确解差别不大，最大差别出现在算例7，也只有6.3%， 其他11个算例的平均最优适应度值差异为3.26%.以上结果表明，GA对小规模算例是有效的.

4.3 大规模算例

采用CPLEX很难在可接受的时间内求得大规模算例的精确解，因此在GA对小规模算例有效的基础上，采用GA对大规模问题进行求解.与小规模算例一样，每个算例运行20次，取其平均值来减小误差.结果见表2.

通过表2可以看出，对大规模问题：GA能够在较短的时间内得到近似最优解；最优适应度值随着卸箱数量的增加而增大；当卸箱数量相同时，随着AGV，岸桥和箱区数量的增加，最优适应度值变小.从算例13和14可知，当卸箱数量、AGV数量和岸桥数量不变时，箱区数量的增加使最优适应度值减小；从算例17和18可知，当卸箱数量、AGV数量和箱区数量不变时，岸桥数量增加会减小最优适应度值；从算例21和22可知，当卸箱数量、岸桥数量和箱区数量不变时，增加AGV数量会使最优适应度值减小.综合以上分析可以发现，岸桥和AGV数量变化对最优适应度值的影响大于箱区数量变化的影响.因此，在实际的卸船作业中，岸桥和AGV的重要性略大于箱区装卸设备（RMG）的重要性，但同时需要三者之间的协调作业以提高作业效率.

图3为算例13利用GA进行一次求解得到的收敛图.

5 结束语

自动化码头自动导引小车（AGV）调度方案受到岸桥和堆场的影响，提高AGV水平运输效率是增强自动化码头连续作业能力的关键因素之一.鉴于此，本文研究了AGV与轨道式龙门起重机（RMG）的协同调度问题，以最小化卸船任务完工时间为目标，建立了混合整数规划模型.对小规模卸箱作业和大规模卸箱作业进行了算例分析.利用CPLEX求得小规模卸箱作业的精确解，同时与利用遗传算法（GA）求得的解进行比较，验证了GA的有效性；对大规模卸箱作业问题，利用GA求得结果，并给出自动化码头任务调度的优化方案.

本文只考虑了已知卸箱顺序的AGV与RMG的协同调度问题，然而任务调度还受岸桥、AGV和RMG配置数量的影响，如何合理配置多种设施设备的数量成为提高码头作业效率的关键.此外，水平运输是衔接岸桥作业与堆场作业的关键，因此解决AGV水平运输的拥堵、死锁等问题也将会是今后研究的重点.

参考文献：

[1]CHOE R， KIM J， RYU K R. Online preference learning for adaptive dispatching of AGVs in an automated container terminal[J]. Applied Soft Computing， 2015， 38： 647660.

[2]KIM J， CHOE R， RYU K R. Multiobjective optimization of dispatching strategies for situationadaptive AGV operation in an automated container terminal[C]//Association for Computing Machinery （ACM）. Research in Adaptive and Convergent Systems. New York： ACM， 2013： 16.

[3]ANGELOUDIS P， BELL M G H. An uncertaintyaware AGV assignment algorithm for automated container terminals[J]. Transportation Research Part E， 2010， 46（3）： 354366.

[4]MIYAMOTO T， INOUE K. Local and random searches for dispatch and conflictfree routing problem of capacitated AGV systems[J]. Computers & Industrial Engineering， 2015， 91： 19.

[5]邱跃龙， 陶德馨. 基于时间Petri网的集装箱码头AGV调度系统建模研究[J]. 武汉理工大学学报（交通科学与工程版）， 2006， 30（6）： 958960.

[6]马越汇， 胡志华. 不确定环境下自动化集装箱码头AGV调度与配置问题[J]. 广西大学学报（自然科学版）， 2016， 41（2）： 589597.

[7]霍凯歌， 张亚琦， 胡志华. 自动化集装箱码头多载AGV调度问题研究[J]. 大连理工大学学报， 2016， 56（3）： 244251.

[8]康志敏. 集装箱自动化码头AGV路径优化和调度研究[D]. 武汉： 武汉理工大学， 2011.

[9]柯冉绚， 任亚东. 集装箱码头AGV调度优化[J]. 集美大学学报（自然科学版）， 2016， 21（1）： 3541.

[10]MEERSMANS P J M， WAGELMANS A P M. Effective algorithms for integrated scheduling of handling equipment at automated container terminals[C]// ERIM Report Series Research in Management. Rotterdam： Erasmus Research Institute of Management， 2001： 31.

[11]WU Yue， LUO Jianbin， ZHANG Dali， et al. An integrated programming model for storage management and vehicle scheduling at container terminals[J]. Research in Transportation Economics， 2013， 42（1）： 1327.

[12]LUO J， WU Y， MENDES A B. Modelling of integrated vehicle scheduling and container storage problems in unloading process at an automated container terminal[J]. Computers & Industrial Engineering， 2016， 94： 3244.

[13]XIN J， NEGENBORN R R， LODEWIJKS G. Energyaware control for automated container terminals using integrated flow shop scheduling and optimal control[J]. Transportation Research Part C， 2014， 44： 214230.

[14]HAN Y， LEE L H， CHEW E P， et al. A yard storage strategy for minimizing traffic congestion in a marine container transshipment hub[J]. OR Spektrum， 2008， 30： 697720.

（編辑 赵勉）