纬编针织物线圈建模与变形三维模拟

沙 莎， 蒋高明， 张爱军， 丛洪莲

(江南大学 教育部针织技术工程研究中心， 江苏 无锡 214122)

纬编针织物线圈建模与变形三维模拟

沙 莎， 蒋高明， 张爱军， 丛洪莲

(江南大学 教育部针织技术工程研究中心， 江苏 无锡 214122)

为使纬编针织物具有更真实的力学效果和体积感，在改进的弹簧-质点模型基础上对线圈进行结构建模。同时采用插值算法，在相邻型值点间插入2个新的型值点，用非均匀有理B样条曲线(NURBS)连接线圈型值点，解决了NURBS不能穿过所有型值点的问题。为模拟股线的捻度，以此样条曲线为几何中心，用4根圆柱围绕，通过对相邻型值点的空间坐标计算3个相对欧拉角，对圆柱进行相应的旋转变换。测量了真实线圈的形变量，分析出线圈形变量与质点位移量的关系来模拟线圈变形。用Velocity-Verlet数值积分方法求解力学方程，计算各质点位移。借助于Microsoft Visual Studio 2010集成开发工具和OpenGL三维绘图函数库，在计算机上实现了纬编织物的三维建模和变形仿真。

纬编织物； 非均匀有理B样条曲线； 弹簧-质点模型； 旋转矩阵； 线圈变形

线圈的建模和受力很大程度上影响着针织物线圈的形态，2者在仿真方面都是至关重要的。在针织物仿真中，众多学者提出了不同的模型和理论来模拟线圈，其中，Pierce线圈模型是目前线圈仿真中比较有代表性的线圈模型，虽然它假设模型的方法简单，不能很好表现出纬编织物三维的特性[1]。Leaf 模型是对Pierce模型进一步改进，得到了线圈密度与线圈长度之间的关系，能够很好地反应实际织物线圈的密度，但其仍受限于二维模型的本质[2]。Munden 模型假设线圈为完全弹性体，计算出针织物线圈长度与织物尺寸之间的明确数学关系，是基础性的物理模型[3]。为提高线圈模拟的三维特性，学者们开始采用分段函数和样条曲线的方法来建立线圈的几何模型[4-6]。其中，非均匀有理B样条曲线(NURBS)由于具有改变任意控制点而不影响其他曲线形状的优点，被广泛应用于线圈的几何建模中。

由于计算机技术的发展和计算机硬件性能的提高，对于纬编针织物纱线的模拟不再局限于单纯地用直线来代替纱线，而是通过各种几何方法来模拟纱线的纹理及股线效果。如在型值点中间插入亮度随机变化的切片，这个切片由随机的点组成，根据捻度角旋转切片，得到了真实感较强的带毛羽的捻度股线效果，但是，采用这种方法在线圈弯曲位置很难处理[7-8]。Kurbak等[9]将线圈按部位分割成8段，螺旋线绕线圈旋转，虽然增加了线圈的真实感，但是不利于织物的形态控制。于斌成等[10-11]通过若干小球排列、部分相交的办法来模拟股线纹理，再在这些小球上，生成毛羽，真实感强，但不能满足模拟展示的实时性。

对纬编针织物线圈在单纯的几何层面上模拟之后，研究者开始引入力学模型，研究在力的影响下的纬编织物模拟效果。Meissner等[12]引入弹簧-质点模型，用模型中的质点控制线圈的型值点，通过力学计算获得质点的位移和速度，从而获得了真实的织物线圈变化形态。刘瑶等[13-14]在弹簧-质点模型基础上研究质点受力情况，模拟了非均匀组织线圈的受力，计算方法易行，但线圈立体感较弱。Gudukbay等[15]将质点系统多层化，模拟出了立体效果的纬编针织物，但并没有研究非均匀组织的受力变化。雷惠等[16]虽引入了质点模型来模拟线圈的变化，但只研究线圈在纵向的位移变化，对横向上的线圈形态变化并没有研究。

本文在改进的弹簧-质点模型基础上，采用NURBS曲线对线圈进行几何建模。计算出了非均匀组织变形的偏移关系的动态方程，模拟出非均匀组织的线圈形状变化。用21 tex涤纶纱线，在STOLL CMS 3.5.2电脑横机上编织针织物试样，用超景深显微镜拍摄织物试样，并进行尺寸测量，研究线圈的形态变化。

1 线圈模型的建立

1.1 改进的弹簧-质点模型

传统的弹簧-质点模型能够很好地模拟出织物的物理特性，但应用到纬编织物仿真中，由于不能充分表现出纬编织物组织的空间关系，所以不能展示出真实纬编织物组织的三维特性，因此本文通过在改进的弹簧-质点模型基础上，进行线圈建模。图1示出传统的弹簧-质点模型。弹簧分为3种类型：结构弹簧、剪切弹簧与弯曲弹簧。结构弹簧用于保持织物质点间经纬方向的距离；剪切弹簧用于保持织物质点间斜向方向的距离；弯曲弹簧连接经纬方向间隔的2个质点，用于模拟织物弯曲或折叠时的抗弯曲性能[4]。

图1 弹簧-质点模型Fig.1 Mass spring models. (a) Mass connections; (b) Structure spring; (c) Shear spring; (d) Bend spring

由于传统的弹簧-质点模型不能体现出纬编织物的复杂结构和空间关系，因此，为了更好模拟纬编织物的效果，本文将平面的模型立体化，改进后模型如图2所示。各质点均匀分布在空间的网格上，每个小长方体的每条边作为结构弹簧，长方体面上的对角线作为剪切弹簧，由于弯曲弹簧的弹性系数极小，因此在本模型中，将弯曲弹簧忽略。模型的质点是随时间变化的动态系统，在每个时间步长里，质点模拟受内力和外力的作用而移动，线圈上的控制点也随之移动，引起线圈的形变[5]。

图2 改进的弹簧-质点模型Fig.2 Improved spring-mass model

1.2 线圈几何模型

赋予质点物理属性，并将线圈的型值点与弹簧-质点模型建立关联，能够使线圈的形状随着质点受力而产生变化，从而使线圈受力获得真实的物理效果。型值点的位置与线圈的圈高、圈宽、圈柱高等一一对应。通过对织物线圈上各参数的测量来确定型值点的位置，如b5到b9为圈宽。纱线的截面半径根据对实际纱线的截面测量获得。线圈几何模型如图3所示。黑色圆点是模型中的质点，用pi, j, z表示，其中，i代表质点在模型中的第几行，j代表质点在模型中的第几列，z代表质点在模型中的第几层。即p3,1,2是模型中第2层第1列第3行上的质点。BPs是线圈的型值点，用灰色圆点表示。

图3 线圈几何模型Fig.3 Loop geometry model. (a) Front view; (b) Left view

1.3 线圈的参数化处理

型值点用来控制线圈的形状，通过建立BPs与质点的关系来模拟线圈的形态，当织物受力的作用，BPs随着质点的移动而移动，因此可以使线圈产生真实的物理形变。本文以成圈线圈为例，型值点与质点的关系如下：

(1)

(2)

(3)

(7)

(8)

(9)

(10)

(11)

(12)

2 基于NURBS的线圈基本形状建模

Bezier最先在工业设计中运用计算机工具[6]，具有相当多的优点，但当改变线圈的一个控制点，其整条曲线都会改变,而B样条曲线有效控制了这个问题。B样条曲线是由任意数量的曲线段组成的完全的分段多项式，因此，改变一个控制点并不影响其他曲线段的形状。NURBS是一种在B样条曲线中，采用其次坐标来指定的曲线。它统一了Bezier、有理Bezier、均匀有理B样条和非均匀有理B样条。NURBS在获得B样条曲线所有优点的基础上，引入权因子，可以调整线圈形状，并且量化了单个权因子的变化对曲线形状的影响[7]。这样，使NURBS具有更加灵活稳定的特性，被广泛应用于线圈三维模拟中。

2.1 NURBS样条曲线

NURBS曲线是由控制点和分段样条基函数所确定的B样条曲线，其表达式[8]为：

(13)

式中：Pi(i=0,1,2，…,n)是特征多边形控制顶点的位置矢量；Wi是与Pi对应的权因子；Ni,k(u)是k次B样条基函数。

2.2 线圈控制点的插值算法

因为线圈上的型值点分布不均匀，需要曲线二次连续，因此采用三次非均匀有理B样条建立纬编针织物线圈结构模型。NURBS有一个缺点是曲线除了能够穿过首尾2点外，并不能完全穿过所定义的控制点。通过反算控制点的方法虽然可以解决这一问题，但计算量大。为了解决这个问题，本文选用文献[5]的方法，除首尾两端以外，在线圈上相邻的2个型值点间插入2个辅助点，这样就得到了包含型值点的控制顶点。以型值点BP3为例：

(14)

(15)

(16)

式中：Ti(i=0,1,2,…,n),是Pi点处的切点；

根据公式(14)～(16)的方法，新的控制点序列di就形成了。本文的12个型值点更新出11个新控制点(首端和末端只加一个新的控制点)，由此形成了23个控制顶点确定的控制多边形。

2.3 股线效果的模拟

纱线股线是由单纱合股而成，单一的圆柱不能真实的反映出线圈的特征,因此本文用4根圆柱来模拟线圈的股线。以2.3节生成的线圈模型做为几何中心线，4根圆柱围绕此中心线旋转。图4为圆柱截面旋转示意图。

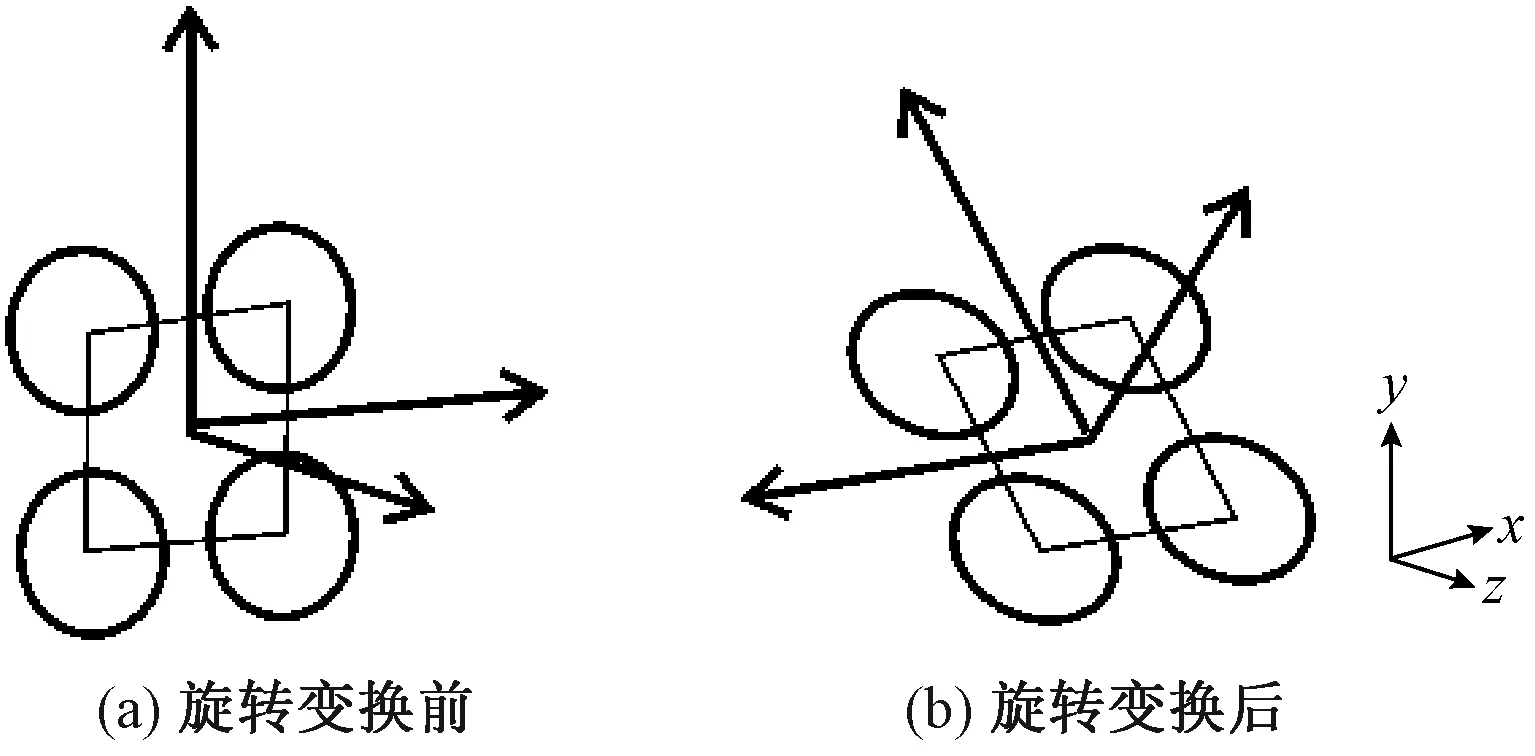
图4 圆柱旋转示意图Fig.4 Cylinder rotate schematic. (a) Before rotation; (b) After rotation

本文假设一个局部坐标系Σ与圆柱在6个刚体自由度上始终保持相对静止，再假设一个始终静止的绝对坐标系Σ0。基于绝对坐标系Σ0来描述局

部坐标系Σ，可以使用3个与局部坐标系Σ的3个坐标轴平行的单位列向量来表示Σ。假设图4(a)位置时Σ与Σ0是重合的，经过某个旋转，Σ从该位置变换到了图4(b)位置。描述坐标系中相互垂直的单位向量可以用矩阵形式来表示，则有以下关系[9]：

(17)

式中：

(18)

式中，T1，T2，T3分别表示3次基本旋转。第1次围绕x轴旋转α角度，第2次围绕y轴旋转β角度，第3次围绕z轴旋转γ角度。三维情况下3个基本旋转的旋转矩阵表示如下。

围绕X轴的基本旋转矩阵为

(19)

围绕Y轴的基本旋转矩阵为

(20)

围绕Z轴的基本旋转矩阵为

(21)

因此，根据式(17)～(21)可得：

(22)

3 纬编线圈的形变

3.1 线圈形变原理

线圈的型值点建立在1.1节长方体弹簧-质点模型的基础上，质点由结构弹簧和剪切弹簧连接。当松弛状态下相同的组织中引入不同的线圈结构，质点受力发生位移，引起关联的型值点也随之发生位移，线圈发生形变。图5示出线圈结构图及质点受结构弹簧力和剪切弹簧力的受力分析图。

图5 线圈受力变形原理Fig.5 Deformation principle of forced loop.(a) Loop structure;(b) Loop forced main view and; (c) lateral view

3.2 线圈形变量计算

将立体模型中的质点标记为Pi，j，k, 质点用三维数组P[i][j][k]表示，如果当2个质点的i，j，k的值只有一个不一样，且这个不一样的值相差1时，连接这2个质点的弹簧被定义为结构弹簧；当2个质点的i,j,k的值只有一个相等，且其他的2个值只相差1时，被定义为剪切弹簧。pos[i][j][k]表示每个质点的位置，根据质点的位置判断弹簧的长度。当弹簧原长l0发生变化变成l1,质点因为受弹簧力和阻尼力而产生位移，从而带动关联的型值点发生位移，产生线圈形状的变化。

本文以集圈线圈的变形计算为例，来说明计算线圈形变的方法。根据对样本的测量，当周围组织为成圈，中心线圈为集圈时，线圈在x/y/z轴上的平均位移量通过Spss分析软件拟合出线圈的变形量，依据方程如下：

(23)

得到线圈的偏移量之后，通过反算质点的方法，能够计算出质点的位移量。根据质点的位移量结合Velocity-Verlet数值积分方法求解力学方程。计算出临近所有质点的位移量。最后通过质点带动型值点，使线圈形状发生变化，产生真实的线圈受力形变。当织物不含有不同类型的线圈时，线圈不发生形变；当织物含有不同类型的线圈时，线圈发生形变。

4 纬编线圈建模与形变的实现

使用Visual Studio和OpenGL实现纬编针织物线圈的建模和渲染，实现过程如图6所示，线圈仿真实现如图7、8所示。

图6 工作流程图Fig.6 Flow chart

图7 花色组织的变形模拟Fig.7 Weft knitted fabric simulation of fancy structures. (a) Simulation of tuck; (b) Shimulation of float; (c) Simulation of loop transfer

图8 花色组织的真实织物Fig.8 Weft knitted fabric of fancy structures. (a) Reality of tuck; (b) Reality of float float; (c) Reality of lop transfer loop transfer

5 结 语

本文针对纬编织物线圈结构的特点，在改进的弹簧-质点模型基础上建立三维线圈参数模型，用NURBS曲线来拟合线圈曲线。通过旋转4根圆柱来模拟纬编织物线圈的股线捻度效果以此来获得具有真实感的均匀纬编织物线圈仿真效果。通过计算弹簧-质点模型中质点的受力来模拟非均匀组织线圈的变形。用Velocity-Verlet数值积分方法求解力学方程，计算各质点位移这种方法计算简练，即保证了动态仿真的实时性，又得到了逼真的纬编织物。

FZXB

[1] PEIRCE F T. Geometrical principles applicable to the design of functional fabrics [J]. Textile Research Journal, 1947, 17 (3): 123-147.

[2] LEAF G V. Models of plain knitted loop [J]. Journal of the Textile Institute, 1960, 51 (2): 49-58.

[3] MUNDEN D L. Geometry and dimensional properties of plain-knit fabrics [J]. Journal of the Textile Institute, 1959, 50 (7): 448-471.

[4] CONG H, GE M，JIANG G. Three-dimensional simulation of warp-knitted fabric [J]. Fibres & Textiles in Eastern Europe, 2009, 17 (3): 66-69.

[5] 蒙冉菊，方园. NURBS样条曲线纬编针织物线圈结构的建模分析 [J]. 浙江理工大学学报, 2007, 24(3): 219-224. MENG Ranju, FANG Yuan. The modeling analysis of knitted fabric loop construction using NURBS curve [J]. Journal of Zhejiang Sci-Tech University, 2007, 24(2):219-224.

[6] 丛洪莲, 葛明桥, 蒋高明. 基于NURBS曲面的经编针织物三维模型 [J]. 纺织学报, 2008, 29(11): 132-136. CONG Honglian, GE Mingqiao, JIANG Gaoming. 3-D modeling for warp knitted fabric based on NURBS [J]. Journal of Textile Research, 2008, 29(11): 132-136.

[7] CHEN Y Y, LIN S, ZHONG H, et al. Realistic rendering and animation of knitwear [J]. IEEE Transactions on Visualization and Computer Graphics, 2003, 9 (1): 43-55.

[8] ZHONG H, XU Y Q, GUO B N，et al. Realistic and efficient rendering of free-form knitwear [J]. Journal of Visualization and Computer Animation, 2001, 12 (1): 13-22.

[9] KURBAK A, KAYACAN O. Basic studies for modeling complex weft knitted fabric structures: part II: a geometrical model for plain knitted fabric spirality [J]. Textile Research Journal, 2008, 78 (4): 279-288.

[10] 吴周镜, 宋晖, 李柏岩, 等. 纬编针织物在计算机中的三维仿真 [J]. 东华大学学报(自然科学版), 2011, 37(2): 210-214. WU Zhoujing, SONG Hui, LI Baiyan, et al. 3D simulation of weft knitted fabric in computer [J]. Journal of Donghua University (Natural Science Edition), 2011, 37(2): 210-214.

[11] 于斌成, 李柏岩, 刘晓强, 等. 一种增强模拟纬编针织物外观真实感的方法 [J]. 东华大学学报(自然科学版), 2013, 39 (5): 644-649. YU Bincheng, LI Baiyan, LIU Xiaoqiang, et al. A method to improve the sense of reality of simulated weft knitted fabric appearance [J]. Journal of Donghua University (Natural Science Edition), 2013, 39(5): 644-649.

[12] MEISSNER M，EBERHARDT B. The art of knitted fabrics, realistic & physically based modelling of knitted patterns [J]. Computer Graphics Forum, 1998, 17(3): 355-362.

[13] 刘瑶, 邓中民. 羊毛衫组织的变形分析及三维仿真新方法 [J]. 针织工业, 2012(2): 21-23. LIU Yao, DENG Zhongmin. The deformation analysis and the simulation realization of woolen sweater [J]. Knitting Industries, 2012(2): 21-23.

[14] 赵磊. 纬编针织物线圈的三维模拟及变形实现 [D]. 武汉:武汉纺织大学, 2011: 34-56. ZHAO Lei. Three-dimensional simulation and deformation realization of weft loop [D]. Wuhan: Wuhan Textile University, 2011: 34-56.

[15] GUDUKBAY U, BAYRAKTAR S, KOCA C, et al. Particle-based simulation of the interaction between fluid and knitwear [J]. Signal Image and Video Processing, 2014, 8 (3): 415-422.

[16] 雷惠, 丛洪莲, 张爱军, 等. 基于质点模型的横编织物结构研究与计算机模拟 [J]. 纺织学报, 2015, 36(2): 43-48. LEI Hui, CONG Honglian, ZHANG Aijun, et al. Research of flat knitted structure and computer simulation based on particle model [J]. Journal of Textile Research, 2015, 36(2): 43-48.

[17] PROVOT X. Deformation constraints in a mass-spring model to describe rigid cloth behavior [C]//In Proceedings of Graphics Interface[s.l.]. Canadian Human-Computer Communications Society, 1995: 47-54.

[18] 沙莎, 蒋高明, 马丕波, 等. 基于改进弹簧-质点模型的纬编织物三维模拟 [J]. 纺织学报, 2015, 36(2): 111-115. SHA Sha, JIANG Gaoming, MA Pibo, et al. 3-D simulation of weft knitted fabric based on improved mass-spring model [J]. Journal of Textile Research, 2015， 36(2)： 111-115.

[19] BEZIER P E. Numericl control-mmathematics and applications [J]. International Journal for Numerical Methods in Engineering, 1972, 6 (3): 240-456.

[20] 施法中. 计算机辅助几何设计与非均匀有理B样条 [M]. 北京: 高等教育出版社, 2001:32-48. SHI Fazhong. Computer Aided Geometric Design and Non-uniform Rational B-spline [M]. Beijing: Higher Education Press, 2001:32-48.

[21] RAJAB K, PIEGL L A, SMARODZINAVA V. CAD model repair using knowledge-guided NURBS [J]. Engineering with Computers, 2013, 29 (4): 477-486.

[22] 张贤达. 矩阵分析与应用 [M]. 北京: 清华大学出版社, 2013:23-35. ZHANG Xianda. Matrix Analysis and Applic-ations [M]. Beijing: Tsinghua University Press, 2013:23-35.

Three-dimensional modeling and deformation for weft knitted fabric loops

SHA Sha, JIANG Gaoming, ZHANG Aijun, CONG Honglian

(EngineeringResearchCenterforKnittingTechnology,MinistryofEducation,JiangnanUniversity,Wuxi,Jiangsu214122，China)

In order to obtain mechanical behaviors and volumetric characteristics of weft knitted fabric, a loop model was built on the improved mass-spring model. The problem that the non-uniform rational B spline curve (NURBS) can not pass through all bonding points was solved by using the interpolation algorithm which can form new bonding points and the points are linked by NURBS. In order to simulate the twist of folded yarn, the NURBS is regarded as the geometric center with four cylinders around. Three relative Euler angles were calculated by the spatial coordinates of adjacent points. The relationship between the variables of the loop and the displacement of the mass was analyzed by measuring the variables of the loop. The displacement of the mass and mechanics equations were calculated by Velocity-Verlet numerical integration methods. Based on the Microsoft Visual Studio 2010 integrated development tools and OpenGL 3-D graphics library, 3-D simulation of weft knitted fabrics can be realized visually on the computer screen.

weft knitted fabric; non-uniform rational B spline curve; mass-spring model; rotation matrix; loop deformity

10.13475/j.fzxb.20161000107

2016-10-08

2016-11-14

国家科技支撑项目(2012BAF13B03)；国家自然科学基金项目(11302085)；江苏省普通高校学术学位研究生创新计划项目(KYLX15_1161); 中央高校基本科研业务费专项资金项目(JUSRP51404A)

沙莎(1987—)，女，博士生。主要研究方向为针织服装数字化设计。蒋高明，通信作者，E-mail: jgm@jiangnan.edu.cn。

TS 184

A

获奖说明：本文荣获中国纺织工程学会颁发的第17届陈唯稷优秀论文奖