基于随机须丛逐步分解模型的纤维长度分布计算方法

金敬业， 王府梅， 徐步高

(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620；3. 北得克萨斯大学， 得克萨斯州 76203 ，美国)

基于随机须丛逐步分解模型的纤维长度分布计算方法

金敬业1，2， 王府梅1，2， 徐步高1，3

(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620；3. 北得克萨斯大学， 得克萨斯州 76203 ，美国)

为解决新的纤维长度测量方法随机须丛影像法分析纤维长度分布的瓶颈技术，建立了从随机须丛中分离出一定长度界限以下纤维的逐步分解模型，推导出通过须丛线密度曲线的离散点运算获得纤维长度一次累积分布和频率分布的计算公式，避免了以往对须丛线密度曲线二次微分求取长度频率分布时，测量噪声被微分运算放大导致结果失真的问题。将运用逐步分解模型的随机须丛影像法与单纤维测量法测得的纤维长度频率分布直方图进行了对比。结果显示：2种方法测得的棉、毛试样各个长度组质量分数的平均差异分别为0.31%和0.26%，最大差异均小于1%，证明逐步分解模型计算公式具有实际应用价值，可用于纤维长度测量仪器的数据处理。

长度分布； 纤维测量； 随机须丛； 逐步分解模型； 直方图

长度是判断纺织纤维品质性能与使用价值的重要依据，是纤维分级、贸易与加工时的必检项目。目前，不同类型的纤维和应用场合使用的长度测量方法不尽相同，多数需要先测出纤维的某种长度分布，才能算出几项长度指标。常见的长度分布类型有质量(或根数)频率分布、一次累积分布(如手排图)和二次累积分布，三者之间存在微积分关系。理论上讲，获得了任何1种就能换算成另外2种并算出所有长度指标[1-2]，因此，测出准确的长度分布至关重要。

传统上常用罗拉法和梳片法测得棉、毛纤维的长度频率分布直方图及长度指标，测量时纤维先被整理成一端平齐的须丛，再被分组称量；这类方法效率较低，且测量结果易受操作者手工技术的影响，已逐渐被自动化仪器取代[2]。

目前，测量棉型纤维长度常用的自动化测量仪器有AFIS (Advanced Fiber Information System) 和HVI (High Volume Instrument )。AFIS首次实现了对单纤维长度的自动化快速测量，可基于3 000根单纤维的长度数据输出长度频率分布直方图、一次累积分布曲线和一些长度指标；缺点在于纤维被刺辊分离时可能发生断裂，部分纤维未能完全分离[3-5]。HVI是国际棉花交易中常用的测量仪器，其长度测量原理为Hertel纤维照影机，基于须丛曲线计算平均长度、上半部平均长度等指标。HVI随机夹取散纤维的制样方式效率较高，取样量大，但须丛中每根纤维在夹子中的长度不等，少数纤维可能被夹持2次以上，且梳理和测量难以贴近夹持线，由须丛透光信号计算纤维量的方法也较落后，都会导致测量结果存在缺陷，例如其短绒测量结果就一直未被美国棉花分级系统所接受[6-7]。

毛型纤维长度的自动化测量仪器有Almeter和OFDA4000。前者用电容式传感器检测一端平齐须丛，获得一次累积分布曲线，进而换算成长度频率直方图，再计算长度指标；缺陷是电容传感器测量精度低，输出结果与办公自动化设备不能无纸连接等。后者基于图像检测技术对一端平齐须丛每隔5 mm检测1次横截面的纤维根数，测量多个须丛后得到长度的一次累积分布曲线[8]。

上述自动化仪器的共同缺陷是硬件庞大、机电装置复杂、价格昂贵。王府梅等[9]发明了一种基于双端随机须丛的快速、低成本纤维长度测量方法——随机须丛影像法，先制作随机须丛，获得其透光图像，再从图象中提取须丛线密度曲线(简称须丛曲线)，最后计算各项长度指标；近期又研究出由须丛透光信号计算任一像素点纤维量的精确算法，从而提高了须丛曲线的准确性。实验证明，上述方法测出的质量加权平均长度、主体长度、品质长度和长度变异系数与AFIS的测量结果高度一致[10]。然而，如果根据他们推导出的理论关系[11]对须丛曲线进行二次微分求长度频率分布，测量信号中存在的多频率噪声会被微分运算放大，导致计算结果严重失真，常用降噪方法的效果都不理想。

本文针对双端随机须丛的双侧分布特点，提出随机须丛的逐步分解模型，推导出通过须丛曲线离散点的运算获得纤维长度一次累积分布和频率分布的计算公式，无需微分即可把须丛曲线转换成纤维长度一次累积分布图和频率分布直方图，解决了随机须丛影像法仪器化的瓶颈问题。通过与单纤维测量法测出的棉、毛纤维长度分布进行对比，考查该长度分布计算方法的准确性。

1 随机须丛与纤维长度分布

双端随机须丛的制样方法：首先，利用纤维引伸器或牵伸装置将待测试样制成纤维平行伸直、随机排列的条子；然后，以专用钳夹在垂直于条子轴向的任一横截面将其夹紧；最后，梳去夹持线两侧未被夹住的浮游纤维，得到如图1所示的双端随机须丛。图2示出了双端随机须丛的实测须丛曲线F(l)，其中lm代表纤维最大长度。

图1 双端随机须丛Fig.1 Random-beard

图2 双端随机须丛的须丛曲线Fig.2 Fibrogram of random-beard

吴红艳等[13]推导证明，在纤维等线密度的假设条件下，双端随机须丛的长度根数频率分布f(l)等于待测试样的长度质量频率分布pw(l)，即：

(1)

可以推得，随机须丛中长度不大于α(mm)纤维的根数百分比，Sf(α)等于待测试样中长度不大于Sf(α)的纤维的质量百分比Spw(α)，即

(2)

本文逐步分解模型展示了由实测须丛曲线F(l)通过离散点运算求取Sf(α)的原理与方法，求出Sf(α)即得到Spw(α)。当长度界限α取一系列不同值，由Spw(α)可得待测试样的长度质量一次累积分布，并能进一步算出长度质量频率分布。

2 逐步分解模型及其数学表达

2.1 逐步分解模型

在双端随机须丛中，长度不大于α的纤维只分布在l∈[-α,α]区间之内，因此，可以通过一系列假想操作对随机须丛进行分解，将长度不大于α的纤维分离出来。

图3 第1阶段分解示意图Fig.3 Diagram of first stage of separation

图4 第2阶段分解示意图Fig.4 Diagram of second stage of separation. (a) Separation of new beard 1; (b) Separation of new beard 2

图5 第3阶段分解示意图Fig.5 Diagram of third stage of separation

以此类推，将双端随机须丛逐步分解，每个须丛分解出的前2个新须丛均含有一些长度不大于α的纤维，因此在下一阶段被继续分解，而第3个新须丛的纤维长度都不大于α。随着分解的进行，长度不大于α的纤维被越来越多地分离出来，即新须丛3、6、9、12……，它们的合计根数与原始随机须丛纤维总根数之比逐渐逼近Sf(α)；同时，混在其他新须丛中的长度不大于α的纤维越来越少，直至可以忽略不计。

下面将分析说明由实测须丛曲线F(l)计算新须丛3、6、9、12……中纤维根数的方法。

2.2 新须丛中纤维根数的分析与计算

图2所示的须丛曲线F(l)表征了双端随机须丛各横截面处纤维相对根数的变化情况，l=0处纤维根数最多，即F(0)=1，并且

(3)

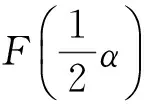
(4)

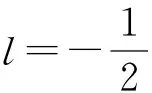
图6 原始随机须丛的须丛曲线分解Fig.6 Fibrogram separation of random-beard

(5)

(6)

(7)

结合公式(3)和(4)，简化为

(8)

由于新须丛2与虚拟须丛2的差别仅涉及长度大于α的部分纤维，长度不大于α的那部分纤维根数相等，且虚拟须丛2与新须丛1对称相等，因此可得

(9)

(10)

图7 新须丛1的须丛曲线分解Fig.7 Fibrogram separation of new beard 1

(11)

(12)

代入式(3)、(4)和(10)可简化为

(13)

此外，类似公式(9)，不难推得公式(11)右侧其他二项也相等，即

(14)

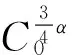
(15)

其中，

(16)

(17)

图8 新须丛4的须丛曲线分解Fig.8 Fibrogram separation of new beard 4

2.3 一次累积分布计算公式的推导

总结前几个阶段新须丛纤维根数的计算规律，建立逐步分解模型的一般化公式，从而推导Sf(α)的计算公式。

(18)

(19)

把m=0,1,2,3,…,n-1依次代入公式(19)，可得方程组

(20)

(21)

把m=0,1,2,3,…,n-1依次代入公式(18)，可得方程组

(22)

将方程组(22)代入公式(21)，整理可得

(23)

令m=n，公式(19)等号两端同乘2n，可得如下变形式：

(24)

(25)

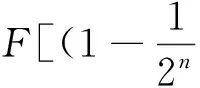
在本文中，取n=5，式(25)变为

(26)

再结合公式(2)，可得

3 纤维长度质量频率分布的计算

以k为隔距，赋予长度界限α一系列不同的值，即α=0,k, 2k, …,ik, (i+1)k, …(其中i为自然数)，则式(27)转化为表1所示的一系列算式。以α为横坐标、相应算式的计算结果为纵坐标，可得待测试样的长度质量一次累积分布曲线。

表1 长度质量一次累积分布的系列算式Tab.1 Formulas for calculating length-weight cumulative distribution

用表1中相邻两算式的后者减去前者，可得到以k为组距的一系列长度组的质量分数，即长度在ik与(i+1)k之间的纤维质量分数Pw(ik)可由下式计算：

(28)

式中i为自然数。

4 实验验证

为考查上述长度分布计算方法的可行性和准确性，分别选取棉、毛纤维试样各1种。每种试样制作3个须丛，利用随机须丛影像法测出须丛曲线，并求3个须丛曲线的均值得到平均须丛曲线。对平均须丛曲线进行均值滤波平滑处理后，应用表1计算各个长度界限以下纤维的质量分数(即一次累积分布)，并用式(28)计算各个长度组的质量频率，图9、10分别示出棉、毛纤维长度分布图，其中棉、毛试样的组距分别为2、6 mm。

图9 2种方法测出的棉纤维长度分布直方图对比Fig.9 Length histogram of cotton sample from two measuring methods

图10 2种方法测出的毛纤维长度分布直方图对比Fig.10 Length histogram of wool sample from two measuring methods

图9、10给出最客观、准确的GB/T 16257—2008《纺织纤维 短纤维长度和长度分布的测定 单纤维测量法》的测量结果，作为本文方法的对比。显然，分别用本文方法和基础方法测得的长度分布直方图趋势非常一致，2种方法测得的棉、毛试样各个长度组质量分数的平均差异分别为0.31%和0.26%，最大差异均小于1%。说明本文介绍的新计算方法具有很高的精度和应用价值。

在后续研究中，将采用更多试样，并把运用本文计算公式的随机须丛影像法与现有仪器的测量结果进行对比。

5 结 论

针对随机须丛影像法纤维长度测量系统仪器化工作中碰到的难题，建立了双端随机须丛的逐步分解模型，推导出须丛曲线的离散转换公式，无需微分即可把须丛曲线最终转换成长度频率分布直方图，从而巧妙避开了由须丛曲线二次微分求取长度频率分布时信号噪声引起的巨大误差。棉、毛纤维实验表明，本文方法测量计算的纤维长度分布与单纤维测量法的结果一致，说明本方法准确有效。

运用本文的新计算方法，能把随机须丛信号准确转换成待测试样的长度质量一次累积分布和频率分布，并计算任意长度指标。该方法在国际上首次使由随机须丛信号获得纤维长度分布的全部信息成为可能，不仅适用于双端随机须丛，也可用于类似HVI系统的单端随机须丛。

FZXB

[1] KROWICKI R, THIBODEAUX D, DUCKETT K. Generating fiber length distribution from the fibro-gram[J]. Textile Research Rournal, 1996, 66(5): 306-310.

[2] 于伟东. 纺织材料学[M].北京: 中国纺织出版社, 2006: 64-68. YU Weidong. Textile Materials[M]. Beijing: China Textile & Apparel Press, 2006: 64-68.

[3] BRAGG C K, SHOFNER F M. A rapid, direct measurement of short fiber content[J]. Textile Research Rournal, 1993, 63(3): 171-176.

[4] KRIFA M. Fiber length distribution variability in cotton bale classification: interactions among length, maturity and fineness[J]. Textile Research Journal, 2012, 82(12): 1244-1254.

[5] CAI Y, CUI X, RODGERS J, et al. An investigation on different parameters used for characterizing short cotton fibers[J]. Textile Research Journal, 2011, 81(3): 239-246.

[6] THIBODEAUX D, SENTER H, KNOWLTON J L, et al. A comparison of methods for measuring the short fiber content of cotton[J]. The Journal of Cotton Science, 2008, (12): 298-305.

[7] ZEIDMAN M I, BATRA S K, SASSER P E. Determining short fiber content in cotton, Part II: measures of SFC from HVI Data&mdash-Statistical models[J]. Textile Research Journal, 1991, 61(2): 106-113.

[8] GRIGNET J. Microprocessor improves wool fiber-length measurement and extends the applicaton. I. general description of the system and a review and examples of its application[J]. Textile Research Journal, 1981, 51(3): 174-181.

[9] 王府梅, 吴红艳. 一种纤维长度快速低成本测量方法: 中国, ZL 2012 1 0106711.8[P]. 2012-08-22. WANG Fumei, WU Hongyan. A rapid and low-cost method for fiber length measurement: China, ZL 2012 1 0106711.8[P]. 2012-08-22.

[10] WU H Y, WANG F M. Dual-beard sampling method for fibre length measurements[J]. Indian Journal of Fibre & Textile Research, 2014, 39(1): 72-78.

[11] 吴红艳. 一种纤维长度快速低成本测量方法[D]. 上海: 东华大学, 2013:1-20. WU Hongyan. A rapid and low-cost method for fiber-length measurement[D]. Shanghai: Donghua University, 2013:1-20.

Method for calculating fiber length distribution based on hierarchical model of random-beard

JIN Jingye1,2， WANG Fumei1,2， XU Bugao1,3

(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China； 2.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China； 3.UniversityofNorthTexas,Texas76203,USA)

A special hierarchical model was proposed to overcome the bottleneck on the fiber length distribution analysis by a random-beard image method, which is a new method for fiber length determination. Based on the two-end characteristic of random-beard, the model could figure out the proportion of fibers shorter than certain thresholds, and derive out a series of formulas for converting fibrogram to cumulative diagram and length frequency histogram via discontinuous point operations, avoiding the previous differential operations which magnified the measurement noise and led to serious measurement errors. Both cotton and wool were tested, respectively with the gauge of 2 mm and 6 mm, using these formulae and a single fiber measurement method. The histograms show that the mean differences of the weight frequencies of the length groups from the two methods, are 0.31% and 0.26%, respectively, and the differences are all less than 1%, which means the measurements from the two methods have a good agreement. The new calculation method in this paper is highly precise and valuable for the data processing of fiber length measuring instruments.

length distribution; fiber measurement; random-beard; hierarchical model; histogram

10.13475/j.fzxb.20161001509

2016-10-09

2016-10-27

国家自然科学基金项目(NSFC 51673036)；中央高校基本科研业务费专项基金项目(CUSF-DH-D-2014009)

金敬业(1985—)，男，博士生。主要研究方向为纺织材料检测技术。王府梅，通信作者，E-mail：wfumei@dhu.edu.cn。

TS 101.1

A