基于临界滑脱长度的短纤纱断裂强力计算

姜 展， 孙 娜， 杨建平， 郁崇文，2

(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620)

基于临界滑脱长度的短纤纱断裂强力计算

姜 展1， 孙 娜1， 杨建平1， 郁崇文1，2

(1. 东华大学 纺织学院， 上海 201620； 2. 东华大学 纺织面料技术教育部重点实验室， 上海 201620)

为得到一种更加合理的短纤纱断裂强力的近似计算方法，根据短纤纱结构的理想化假设和临界滑脱长度的概念，推导出短纤纱断裂过程中纤维临界滑脱长度的近似计算表达式以及发生断裂和滑脱的纤维对短纤纱断裂强力的实际贡献。鉴于短纤纱截面纤维根数的不匀，根据计算得到的临界滑脱长度采用纤维在短纤纱中随机排列的模拟对短纤纱断裂强力进行计算。通过纺制不同线密度下具有不同捻系数的粘胶纱与涤纶纱，并测试其断裂强力对该计算方法进行验证。计算和验证结果表明：临界滑脱长度的计算值随着捻系数的增加而减小，且当捻系数增加时，短纤纱断裂强力的计算值随着捻系数的增加升高至最高值而后发生下降，这与实测短纤纱强力值的变化趋势是一致的。

短纤纱强力； 临界滑脱长度； 捻系数； 有效纤维强力； 滑脱摩擦力

纱线断裂机制的探索一直以来都是纺织领域里的经典课题之一。众所周知，在短纤纱断裂过程中其断裂截面上的纤维会发生滑脱或者断裂，许多研究者们也针对纤维拉伸过程中的状态进行了数学建模与分析，以能够实现纱线断裂强力的预测。Hearle[1-2]、Pan[3-4]及Frydrych[5-6]等人分别采用力学建模的方法对短纤纱断裂过程中纤维的滑脱和断裂机制进行了研究，Pan[7]、Shao[8-9]等还采用了束链模型来分析纤维与纱线强力之间的关系，然而他们得到的力学表达式过于复杂，且含有大量不能表征或测量的参数，因此他们的研究仅能作为定性的理论分析而不能用于实际纱线强力的预测。

为能够对纱线断裂截面中纤维的滑脱和断裂进行判定和描述，在多数研究中均引入了临界滑脱长度的概念。由于纤维在加捻过程受到周围纤维压应力的作用，在纱线拉伸过程中纤维之间存在相对滑移而产生摩擦力，当纤维表面的滑动摩擦力恰好累积等于纤维本身断裂强力时的长度就称为临界滑脱长度。Zeidman[10]、严广松[11]、Jiang[12]分别采用几何概率的方法，根据纤维的长度分布与临界滑脱长度的关系分析了纱线断裂强力的组成：发生滑脱的纤维对纱线断裂强力的贡献是它滑移时所受的滑脱摩擦力，发生断裂的纤维对纱线断裂强力的贡献是它们本身的断裂强力，2部分纤维对纱线强力的贡献之和就是纱线的最终断裂强力。然而他们的研究中并没有给出临界滑脱长度的计算，使得他们对纱线断裂强力也仅为定性地描述。

许多研究也对临界滑脱长度的计算进行了探讨。如Gregory[13]考虑了等长纤维纱中纤维表面与发生相对滑动趋势的纤维相接触的概率推导出临界滑脱长度的计算式；Pan[4]根据纱线应力转移的机理计算了纤维的滑脱率，从而间接得到临界滑脱长度；Yan[14]基于Zeidman[10]的研究进一步考虑了纤维截面与纤维强力之间的关系，得到了临界滑脱长度的表达式。然而这些临界滑长度的计算中仍存在无法表征或测量的参数，此外Gregory和Yan的研究没有考虑纱线结构(如捻度)对临界滑脱长度的影响，使得临界滑脱长度仍不能得到求解。

本文研究将基于短纤纱结构与力学分析对纱线断裂时纤维的临界滑脱长度进行近似推导，并进一步探讨断裂截面中发生滑脱和发生断裂的纤维对短纤纱断裂强力的贡献，得到短纤纱断裂强力的近似计算方法。计算结果将与实际纺纱试验结果进行对比以验证计算方法的合理性。

1 计算模型的建立

1.1 临界滑脱长度的近似计算

对正常受到拉伸的短纤纱中取1根纤维进行分析，如图1所示。该纤维表面由于加捻作用受到压应力q的作用，且纤维之间存在相对滑移趋势，因此在该纤维表面就存在滑动摩擦力ps的作用。该摩擦力从纤维头端起逐渐累积增加，一直达到该纤维本身的断裂强力pf时(AB或CD段)摩擦力便不再增加，该纤维就会在BC段上发生断裂，AB与CD段的长度就称为临界滑脱长度lc。

图1 临界滑脱长度的示意图Fig.1 Schematic view of critical slipping length

由于短纤纱结构的复杂性，纱中每根纤维的受力状态都会有所不同，因而每根纤维断裂时的临界滑脱长度也不相同。为简化计算，我们假设用于计算短纤纱断裂强力的临界滑脱长度值lc是定值。通常对于大多数环锭纱来说，纤维在纱体中都是呈螺旋缠绕的，所求的临界滑脱长度值lc可表示为短纤纱中各根纤维沿其轴向的临界滑脱长度在纱轴方向上分量的均值。为便于计算，假设纱中各根纤维沿其轴向的临界滑脱长度值均为相等的，其值等于短纤纱表面纤维沿其轴向的临界滑脱长度lco。在计算之前，还需对纤维性能和短纤纱的结构进行如下假设：1)短纤纱的结构为圆柱体，即短纤纱所有的横截面为圆形且具有相同的直径；2)所有的纤维具有相同的力学性质，且它们的应力-应变关系服从胡克定律；3)不考虑纤维在纱中的内外转移、捻缩以及加捻过程中纤维之间的相互滑移。

取短纤纱表面层纤维临界滑脱长度位置处(即图1的CD部分)长度为dl的微元进行力学分析，它离纤维最近头端的距离l不超过lco，如图2所示。令L为纤维长度，mm；φ、dφ分别为纤维段l、dl对应的包角；T、T+dT分别为微元dl上两端的张力,cN；q、dq分别为由于加捻在l与dl上产生的向心压力，cN；μ为纤维之间的摩擦因数；pf为纤维的断裂强力，cN。对微元dl，在法向方向上可得到力学平衡式：

(1)

在切向方向上可得到力学平衡式：

(2)

其中

(3)

(4)

图2 临界滑脱长度计算的力学分析Fig.2 Mechanical analysis of critical slipping length

由于本文研究中不考虑短纤纱的捻缩，表面层纤维在加捻后长度会伸长为Lsecβ[15]，因此表面层纤维在加捻后的伸长率ε0=(Lsecβ-L)/L=secβ-1。

(5)

式中：Ef为纤维模量，cN/tex；Nf为纤维线密度，tex。所以表面层纤维因加捻产生的初始张力T0，cN。εf为纤维的断裂伸长，则Ef=pf/(εfNf)。那么根据临界滑脱长度的定义，表面层纤维临界滑脱长度lco的最终计算表达式可由式(4)积分得到下式

(6)

根据假设条件，所求lc为短纤纱各位置纤维的临界滑脱长度lco沿纱轴方向上分量的均值。取位于短纤纱横截面半径为r(r≤R)处的纤维进行分析，其对应的螺旋角为α(α≤β)，如图3所示。

根据所有纤维沿纤维轴向的临界滑脱长度值都相等的假设，该根纤维轴向方向上的临界滑脱长度沿纱轴方向上的分量为lcocosα。若该根纤维出现在纱截面中任一半径位置上的机率都是相等的，即服从二维均匀分布，那么所求lc可由下式得到：

图3 短纤纱的理想螺旋形几何结构及其圆柱展开图Fig.3 Schematic view of yarn helical structure and its expanded diagram of cylinder. (a) Yarn helical structure; (b) Expanded diagram of cylinder

(7)

式中D表示纱的圆形截面。将式(7)转化为极坐标形式，就可得

(8)

(9)

将式(9)代入式(8)就可以得到lc的最终表达式：

(10)

短纤纱的半径R可由下式到得[16]：

(11)

式中：R为短纤维半径，mm；δf、δy分别为纤维和纱的质量密度，g/cm3；Vf=δy/δf为短纤纱的填充系数，它表示纤维占纱空间的比值，Vf的求解可由Pan[3]的经验表达式求得：

(12)

纱表面的螺旋角β可由Hearle的公式[17]求得：

(13)

1.2 短纤纱断裂强力的计算

短纤纱发生断裂的示意图如图4所示。假设所有纤维均为伸直状态且平行于纱轴，OO′为纱的断裂截面，AB、CD分别为纤维两端的临界滑脱长度。根据临界滑脱长度的定义，若OO′落在AB或CD之间，即纤维被OO′握持的长度小于lc，那么该纤维就会发生滑脱，如图4中纤维a与纤维c；若OO′落在BC之间，即纤维被OO′握持的长度大于lc，那么该纤维就会发生断裂，如图4中的纤维b。

图4 短纤纱断裂过程的示意图Fig.4 Schematic view of yarn breakage

由此可知，断裂截面中纤维发生滑脱的概率是2lc/L，发生断裂的概率就是(1-2lc/L)。若纤维的断裂强力为pf，发生滑脱的纤维受到的平均滑脱摩擦力为ps，纱断裂截面上纤维根数为N，那么短纤纱断裂强力P可表达为：

(14)

(15)

1.2.1 纤维平均有效断裂强力的计算

仍取位于短纤纱横截面半径为r(r≤R)处的纤维进行分析，其对应的纤维螺旋角为α(α≤β)。根据上面的分析，该纤维由于加捻伸长产生的初始张力T0=(secα-1)EfNf。因此，该纤维的有效强力应为pf-T0，那么该力沿纱轴方向上的分力pb为

(16)

将式(9)代入上式可得

(17)

1.2.2 平均滑脱摩擦力的计算

假设发生滑脱的纤维沿其轴向具有相同的滑脱摩擦力，其值与表面层纤维沿其轴向的滑脱摩擦力pso(cN)相等。如图2所示，根据表面层纤维临界滑脱长度的推导，通过对式(4)进行积分就可得到微段dl上张力T的表达式为：

(18)

那么由于纤维弯曲在dl上产生的向心压力dq为：

(19)

对式(19)进行积分就可得到长度为l(l≤lco)的纤维片段上的向心压力为

(20)

同时可以得到在纤维断裂处(图2中BC段)的向心压力为

(21)

根据断裂截面落在纤维各个位置上的概率为等可能性的假设，可以得到表面层纤维的平均滑脱摩擦力为

(22)

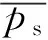
(23)

1.2.3 短纤纱断裂强力的模拟计算

考虑到短纤纱截面纤维根数的差异，本文研究采用了通过模拟纤维在短纤纱的随机排列来计算成纱断裂强力的方法[12]，它能够直观地描述纤维的几何特征对成纱强力的影响。根据纤维左头端沿纱轴方向呈均匀分布的假设[18-20]模拟生成500 mm的纱段，这与实际纱线强力测试采用的试样长度是一致的，如图5所示的MM′到NN′之间的片段。从MM′起将生成的纱段以长度为1 mm的间隔分为若干连续子片段。对于每个分割截面，纤维的滑脱与断裂可通过计算得到的lc判断，且每个截面的强力可通过式(15)计算，其中强力最小值即为短纤纱的断裂强力值。

图5 纤维在短纤纱中随机排列的模拟示意图Fig.5 Schematic view of simulation on fiber random arrangement in yarn

2 计算结果与讨论

采用粘胶纤维与涤纶分别纺制几种线密度的不同捻系数的环锭纱，以对模型计算结果进行验证。粘胶与涤纶纤维的性能如表1所示。

表1 粘胶与涤纶纤维的性能指标Tab.1 Specifications of viscose and polyester fibers

2.1 临界滑脱长度的计算结果

将粘胶纤维与涤纶相关的纤维与成纱参数代入式(10)来计算不同捻系数下的纤维临界滑脱长度lc，结果分别如表2和表3所示。

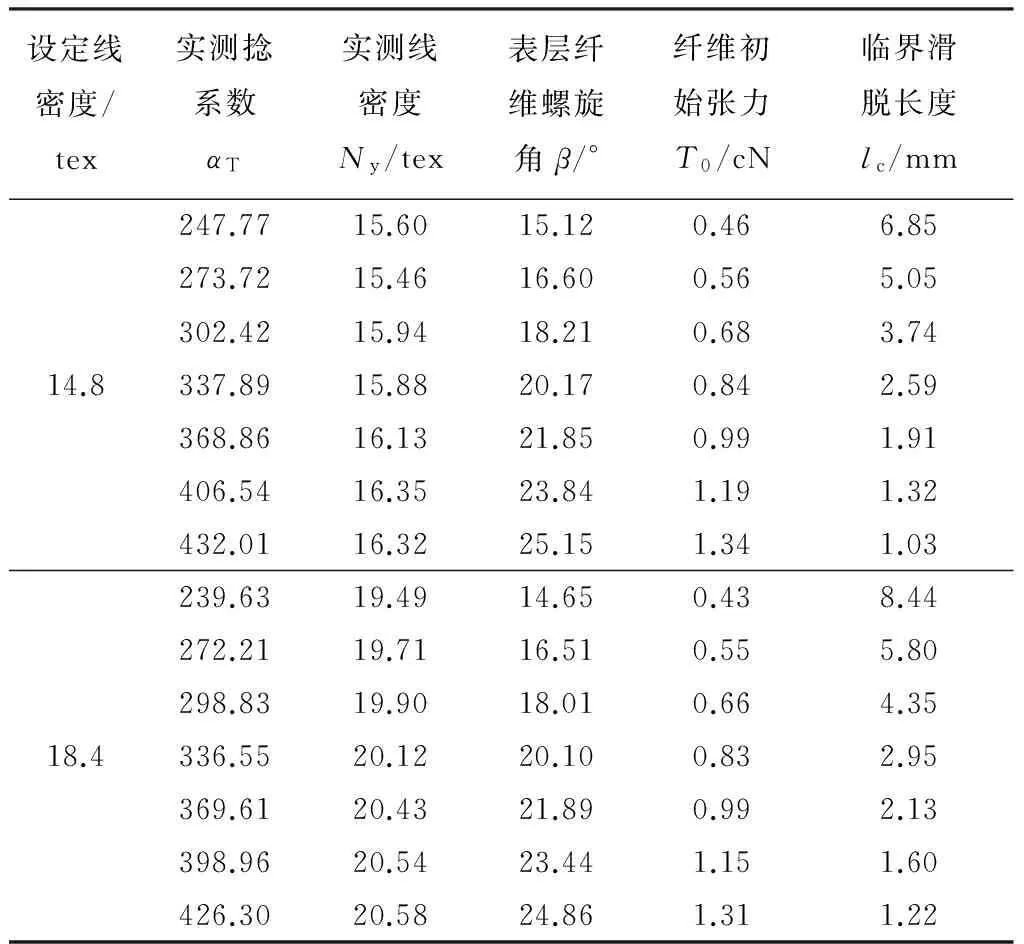
表2 粘胶纱纤维临界滑脱长度的计算结果Tab.2 Calculation of critical slipping length of viscose yarns

从表2和表3可以看出对于粘胶纱和涤纶纱纤维的临界滑脱长度值均随着捻系数的增加呈下降趋势，这是因为随着捻系数的增加表层纤维螺旋角β与纤维初始张力T0均会相应地增加，这导致沿纤维方向摩擦力累积到断裂强力时的长度缩短。此外，也可看出当T0逐渐趋向于纤维的断裂强力pf时lc的下降开始趋于缓慢并逐渐趋向于0。

2.2 短纤纱断裂强力计算的验证

纺制单纱的断裂强力采用YG061单纱拉伸强力仪进行测量，试样夹持长度为500 mm，拉伸速率为500 mm/min，每种纱样测试30次，取其平均断裂强度。测试之前将所有的纱样置于恒温(20 ℃)恒湿(65%)条件下平衡24 h。对每1种根据纤维随机排列模拟得到的单纱，其断裂强度通过模拟计算30次取平均值而求得。2种纱的计算得到的有效纤维强力和平均纤维滑脱摩擦力分别如表4、5所示，纱断裂强度计算值与实测值的对比分别如图6、7表示，计算值与实测的误差也分别列于表4和表5中。

表3 涤纶纱纤维临界滑脱长度的计算结果Tab.3 Calculation of critical slipping length of polyester yarns

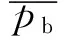
对于纱断裂强力的计算，从图6、7可以看出，粘胶纱与涤纶纱断裂强力的计算值均随着捻系数的增加上升至最高点而后又发生下降，这是与实测值的趋势是吻合的，且在实验设定的捻系数范围内计算值与实测值的误差大多数低于5%。在临界捻系数以前纱强度的上升是由于临界滑脱长度lc的减小使得发生断裂的纤维数目增多，发生滑脱的纤维数目减少，此因素占单纱强力的主导作用，因此单纱强力有升高的趋势；而在临界捻系数之后临界滑脱长度的下降趋于减缓，但由于加捻产生导致纤维的有效强力的剧烈下降以及纤维倾斜导致强力在纱轴方向上的分力减小，这将转变为短纤纱强力的主导因素而最终导致短纤纱纱强力的下降。因此，基于临界滑脱长度的短纤纱断裂强力的计算是合理可靠的。

表4 粘胶纱相关强力参数的计算及 强力计算误差Tab.4 Strength parameters and strength calculation errors of viscose yarns

表5 涤纶纱相关强力参数的计算 及强力计算误差Tab.5 Strength parameters and strength calculation errors of polyester yarns

图6 粘胶纱断裂强度随捻系数的变化曲线Fig.6 Breaking tenacity of viscose yarn versus yarn twist multiplier. (a) Setting yarn count 14.8 tex; (b) Setting yarn count 18.4 tex

图7 涤纶纱断裂强度随捻系数的变化曲线Fig.7 Breaking tenacity of polyester yarn versus yarn twist multiplier. (a) Setting yarn count 14.8 tex; (b) Setting yarn count 19.7 tex

3 结 论

短纤纱在拉伸过程中断裂截面上的纤维可能会发生滑脱或者断裂，这取决于临界滑脱长度。本文研究对临界滑脱长度进行了近似推导，并根据纤维在短纤纱中随机排列的对短纤纱的断裂强力进行了近似计算。由于加捻造成的纤维强力的部分损失，所有发生断裂的纤维对短纤纱强力的贡献应为其有效纤维强力，即纤维强力与初始张力的差值；所有发生滑脱的纤维对短纤纱强力的贡献为其平均滑脱摩擦力。从粘胶纱与涤纶纱断裂强力的计算结果可以看出，短纤纱断裂强力的计算值与实测值随捻系数的变化趋势是一致的。在小于临界捻系数时，临界滑脱长度的下降导致断裂纤维的增多以及滑脱纤维的减少，这使得短纤纱的断裂强力有上升的趋势。而当达到较高捻系数时，增长的纤维初始张力导致纤维有效强力的剧烈下降，这将导致短纤纱强力的降低。因此，该计算方法是合理可靠的，并且当进一步考虑短纤纱的实际结构时可以进一步用于短纤纱断裂强力的预测。

FZXB

[1] HEARLE J W S, THAKUR V M. The breakage of twisted yarns [J]. Journal of the Textile Institute, 1961, 52(2): 49-63.

[2] HEARLE J W S. Theoretical analysis of the mechanics of twisted staple fiber yarns [J]. Textile Research Journal, 1965, 35(12): 1060-1071.

[3] PAN Ning. Development of a constitutive theory for short fiber yarns: mechanics of staple yarn without slippage effect [J]. Textile Research Journal, 1992, 62(12): 749-765.

[4] PAN Ning. Development of a constitutive theory for short fiber yarns: part II: mechanics of staple yarn with slippage effect [J]. Textile Research Journal, 1993, 63(9): 504-514.

[5] FRYDRYCH I. Relation of single fiber and bundle strengths of cotton [J]. Textile Research Journal, 1995, 65(9): 513-521.

[6] FRYDRYCH I. A new approach for predicting strength properties of yarn [J]. Textile Research Journal, 1992, 62(6): 340-348.

[7] PAN Ning, HUA Tao, QIU Yiping. Relationship between fiber and yarn strength[J]. Textile Research Journal, 2001, 71(11): 960-964.

[8] SHAO X, QIU Y, WANG Y. Theoretical modeling of the tensile behavior of low-twist staple yarns: part I: theoretical model [J]. Journal of the Textile Institute, 2005, 96(2): 61-68.

[9] SHAO X, QIU Y, WANG Y. Theoretical modeling of the tensile behavior of low-twist staple yarns: part II: theoretical and experimental results [J]. Journal of the Textile Institute, 2005, 96(2): 69-76.

[10] ZEIDMAN M, SAWHNEY P S. Influence of fiber length distribution on strength efficiency of fibers in yarn [J]. Textile Research Journal, 2002, 72(3): 216-220.

[11] 严广松. 基于密度函数方法的纤维长度分布影响研究 [D]. 上海: 东华大学, 2009: 11-36. YAN Guangsong. Study on the influence of fiber length distribution based on probabilistic density func-tion [D]. Shanghai: Donghua Univeristy, 2009： 11-36.

[12] JIANG Zhan, YANG Jianping, YU Chongwen. Simulation on yarn strength based on fiber random arrangement in the yarn [J]. Journal of The Textile Institute, 2014, 105(2): 209-213.

[13] GREGORY J. Cotton yarn structure: part IV: the strength of twisted yarn elements in relation to the properties of the constituent fibres [J]. Journal of the Textile Institute Transactions, 1953, 44(11): 499-514.

[14] YAN Guangsong, YU Chongwen. A joint influence of the distributions of fiber length and fineness on the strength efficiency of the fibers in yarn[J]. Fibers and Polymers, 2007, 8(3): 309-312.

[15] 于伟东, 储才元. 纺织物理 [M]. 上海: 东华大学出版社, 2002:1-20. YU Weidong, CHU Caiyuan. Textile Physics [M]. Shanghai: Donghua University Press, 2002: 1-20.

[16] 姚穆. 纺织材料学[M]. 第3版. 北京: 中国纺织出版社, 2009: 1-30. YAO Mu. Textile Materials [M]. 3rd ed. Beijing: China Textile & Apparel Press: 2009: 1-30.

[17] HEARLE J W S, GROSBERG P, BACER S. Structural Mechanics of Fibers, Yarns and Fabrics [M]. New York: Wiley-Interscience, 1969: 1-20.

[18] MARTINDLAE J G. A new method of measuring the irregularity of yarns with some observations on the origin of irregularities in worsted slivers and yarns [J]. Journal of the Textile Institute Transactions, 1945, 36: 35-47.

[19] RAO J S. A mathematical model for the ideal sliver and its applications to the theory of roller drafting [J]. Journal of the Textile Institute Transactions, 1961, 52(12): 571-601.

[20] BROWN G H, LY N G. Statistics for the number of fiber ends in a segment of a random assembly of aligned fibers [J]. Textile Research Journal, 1985, 55(4): 206-210.

Calculation of staple yarn strength based on critical slipping length

JIANG Zhan1， SUN Na1， YANG Jianping1， YU Chongwen1,2

(1.CollegeofTextiles,DonghuaUniversity,Shanghai201620,China; 2.KeyLaboratoryofTextileScience&Technology,MinistryofEducation,DonghuaUniversity,Shanghai201620,China)

In order to obtain a more reasonable approach to estimate staple yarn strength, based on idealized assumptions of yarn structure and definition of critical slipping length, the expression of fiber critical slipping length during yarn breaking process was deduced, as well as the actual contributions that breaking and slipping fibers made to yarn strength. Considering variation of fiber number in each yarn cross section, yarn strength was then calculated by simulating fiber random arrangement in the yarn based on the calculated critical slipping length. Viscose and polyester yarns of various yarn counts and twist multipliers were spun and their strengths were tested for calculation and verification. It could be seen from the calculated results that the critical slipping lengths declines with the increase of the yarn twist multiplier. Meanwhile, as the twist multiplier increases, the calculated yarn strength increases to the highest point and then decreases, which is in good agreement with tested results.

staple yarn strength; critical slipping length; twist multiplier; effective fiber strength; slipping frictional force

10.13475/j.fzxb.20161000408

2016-10-04

2016-10-26

国家自然科学基金项目(51173023)；国家农业产业技术体系建设专项(CARS-19)；中央高校基本科研业务费专项基金项目(CUSF-DH-D-2014014)

姜展(1987—)，男，博士生。主要研究方向为纤维的几何特征对成纱质量的影响。郁崇文，通信作者，E-mail：yucw@dhu.edu.cn。

TS 104.1

A

获奖说明：本文荣获中国纺织工程学会颁发的第17届陈维稷优秀论文奖