大数据时代房地产价格预测模型的研究

徐颖 黄素珍

摘 要：大数据时代推动了房地产市场思维方式、管理方式和商业模式的变革。本文利用百度搜索数据，以江苏省南京市为例建立了新建住宅销售价格指数的多元线性回归、完全二次多项式回归和逐步回归模型，仿真结果表明，逐步回归模型预测精度高，稳定性好。

关键词：大数据 百度指数 新房价格 逐步回归模型

中图分类号：F726 文献标识码：A 文章编号：2096-0298（2017）02（a）-134-04

1 引言

2016年12月中旬，中央经济工作会议提出，要坚持“房子是用来住的，不是用来炒的”的定位，要求回归住房居住属性。住房价格高居民承受能力低，居住水平和居住质量会由此下降；反之住房价格水平低，能增强居民的购房能力，相应提高居民的居住水平和居住质量。因此，住房价格的高低成为关系到居民切身利益的重大经济问题和社会问题。

影响房地产价格的因素有很多，如果把所有可能影响的因素全部考虑进去，所建立起来的回归方程却不一定是最好的。首先由于自变量过多，使用不便，而且在回归方程中引入无意义的量，会使误差方差的估计值增大，降低预测的精确性及回归方程的稳定性。另一方面，通常希望回归方程中包含的变量尽可能多一些，特别是对房价有显著影响的自变量，这样会减小误差方差的估计值，从而提高预测的精度。

本文尝试利用百度引擎提供的影响房价的因素搜索指数，建立新建住宅销售价格指数和二手住宅销售价格指数的多元线性回归、完全二次多项式回归和逐步回归模型，仿真结果表明，逐步回归模型预测精度高，稳定性好。

2 房价预测模型构建

3 数据的获取与处理

因变量分别是新建商品住宅销售价格指数。采用2014年1月～2016年8月共32个月的月度同比数据，来源于国家统计局网站。

解释变量是与新房价格相关的某些关键词的网络搜索指数。根据董倩等在文中的方法[2]，对于新房价格预测，最终选取了8个关键词，分别是房价走势、房源、装修、房产网、公积金、房贷利率、新楼盘、保障房。

为了与因变量保持一致，我们对所有关键词的搜索指数做如下处理：首先将根据日搜索指数计算月度平均搜索指数，然后将月度平均搜索指数转换为同比数据，最终得到所有关键词从2014年1月到2016年8月的月度同比数据。

最后将因变量和解释变量的月度同比数据先加1再取对数。

4 仿真分析

本文采用matlab技术，以南京市为例建立和分析新房价格预测模型。

4.1 可视化相关性分析

对表1中的数据按照上述方法进行数据处理，并在matlab中读入处理后的数据，建立因变量矩阵和解释变量矩阵，计算变量间的相关系数矩阵R和线性相关性检验的P值矩阵P，绘制相关系数矩阵图如图1。

4.2 多元线性回归

第一步，模型的建立。

从图3可以看出，残差基本服从正态分布。

第五步，模型改进。

4.4 拟合效果图

上面调用fi t函数作了8元线性回归拟合、6元线性回归拟合和完全二次多项式拟合，得出了3个经验回归方程⑻⑼⑽。拟合效果图如图4所示。

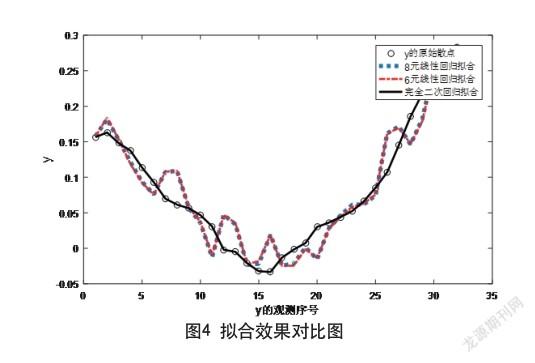
单纯从拟合的准确性来看，完全二次多项式回归拟合的拟合效果较好，8元和6元线性回归拟合的拟合效果差不多，相对都比较差。

4.5 逐步回归

在完全二次多項式回归模型的基础上，利用linearmodel类对象的stepwise方法，经过19次回归，得到二次多项式回归方程如下：

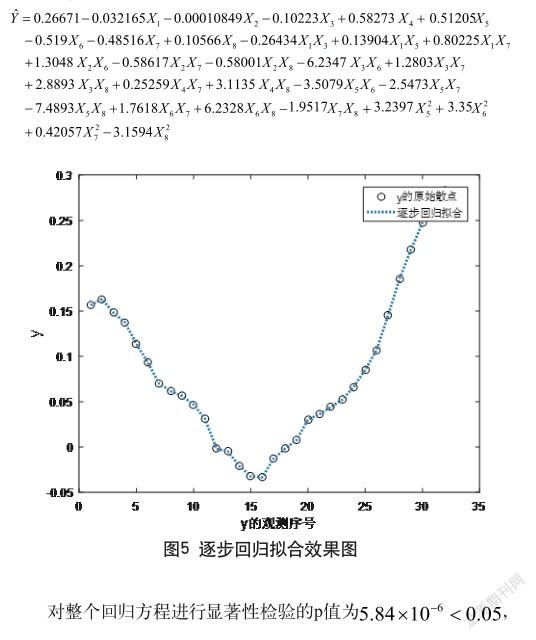
5 结语

房地产行业多年畸形发展催生了畸高的房价，从严调控、保持房地产市场的平稳健康发展被写入多个省份的政府工作报告。本文以百度搜索数据为基础，建立了房价预测的“最优”模型——逐步回归模型，该模型不但可以即时预测房价的走势，而且为地方政府制定调控房价措施提供有效的参考依据。另外，本文建立的房价预测模型还可以拓展到其他城市新房价格的预测和二手房价格的预测，可以预见，在人们利用网络搜索房产信息越来越多的将来，由于搜索数据量越来越大，从而预测的精度会越来越高.

参考文献

[1] 谢中华.MATLAB统计分析与应用[M].北京：北京航空航天大学出版社，2015.

[2] 董倩，等.基于网络搜索数据的房地产价格预测[J].统计研究，2014（10）.

[3] 成鸿飞，等.基于MATLAB的房价预测与调控模型研究[J].科技论坛，2010（6）.

[4] 杨志辉，等.基于MATLAB的房地产销售预测的科学计算[J].统计与决策，2005（1）.

[5] 刘悦婷，等.基于MATLAB的兰州市商品住宅价格变动分析及预测[J].甘肃科学学报，2011（9）.