含参函数的零点问题的处理策略

东北育才双语学校　马江宁

函数是每年高考数学中的必考问题.“含有参数的零点问题”涉及等式的分拆与变形、函数图像和性质的探究，往往要求考生利用多种手段对函数的图像、性质进行研究，并且问题的解决往往涵盖函数与方程、数形结合、分类讨论、转化与化归等四种数学思想，因此备受命题人的青睐，成为近年高考数学中的热点问题.

含参函数的零点问题的特点是参数的不同取值对函数的零点产生影响.从题目形式上看分为两种：一是可分离参数的函数，二是不可分离参数的函数，而后者往往以复合函数的形式出现.下面我们对这两类问题举例研究.

一、可分离参数的函数零点问题的处理策略

例1函数f（x）=x2-ax+1在区间上有零点，则实数a的取值范围是____.

【解析】题意等价于方程x2-ax+1=0，在区间内有解，又x=0不是方程的解，

则f（x）=x2-ax+1的零点问题等价于y=a与y=的交点个数问题，

其图像如下图所示：

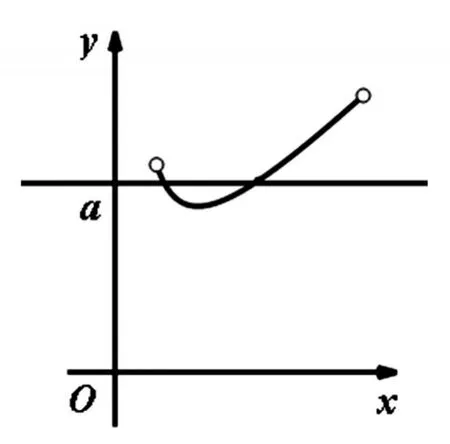
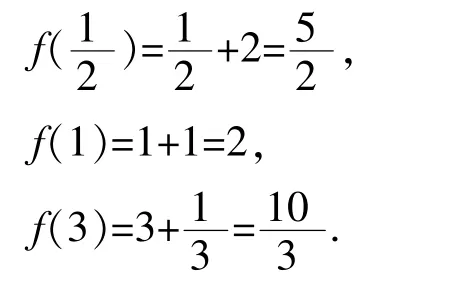
【总结提升】可以分离参数的函数的零点问题往往是：已知函数零点个数，求参数取值范围.解决这类问题，我们可以先把所求变量进行分离，然后画出分离变量后的函数图像 （函数确定，图像固定——静），最后通过平移直线（参数变化，直线平动——动），采用动静结合的方式，形象直观地找符合题意的交点情况进行解答.

同时要学会辩证地处理问题，比如有些题目分离出简单的含参函数更为简洁，接下来只需要考查该函数随着参数的变化规律即可，看下面的例子.

例2已知函数，若函数g（x）=f（x）-k（x-1）恰有两个零点，则实数 k 的取值范围为____.

【解析】题意即求直线 y=k（x-1）与函数 y=f（x）何时有两个交点.

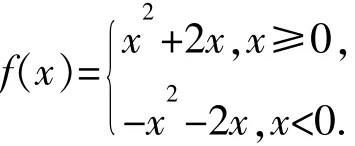
其图像如下图所示：

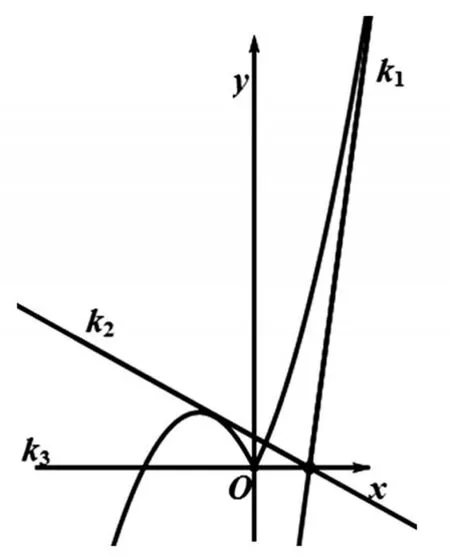
观察图像可知：

①直线 y=k（x-1）过原点或与函数 y=f（x）的图像相切时，函数 g（x）=f（x）-k（x-1）恰有两个零点.

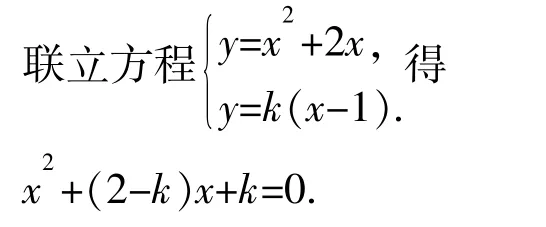
令 Δ=（2-k）2-4k=0，

③直线y=k（x-1）过原点时，即k3=0也符合题意.

综上，所求实数的范围是

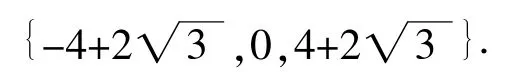
【总结提升】同例1一样，例2利用分离参数的方法，转换成两个函数在定义域内的交点个数问题，不同之处在于例2中分离出的是个一次函数，进而将函数零点个数问题转化成绕一定点的动直线与函数的交点的个数问题.同学们在处理具体问题时，要以分离出哪种形式更简洁、更利于研究函数的性质为原则.

例3已知函数恰有三个零点，则实数m的取值范围是____.

【解析】因为x=0不是函数f（x）的零点，

m=0 时，函数 f（x）无零点，

故只需讨论x，m≠0的情况即可.

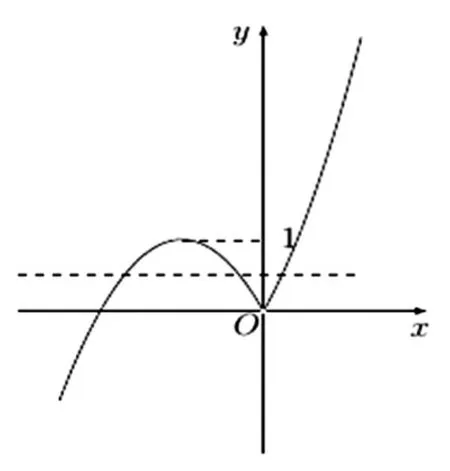
综上，m的取值范围是m＞1.

【总结提升】例3分离参数时，同学们可能采用了不同的分离参数方式，如分离出等，但是为了方便画函数图像，这里采取了分离出.对比以上三个例题，同学们在分离参数时要学会权衡拆分成何种形式更为简洁.

在这里还要提醒同学们在转化与化归过程中，注意方程的等价性，请看下面的例子.

例4若关于x的方程有四个不同的实数根，则实数k的取值范围是____.

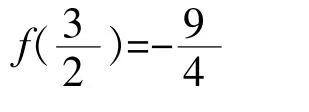
【总结提升】例4和例3的分离参数的方法相同，但是在化简时，两边同时约掉了，注意x=0就是方程的一个解，我们只需要研究化简后的方程有三个不为零的解即可.对比以上两个问题，在分离参数时不仅仅要注意分离的形式不同，还要注意在整理变形时可能会出现导致零点个数发生改变的情况.

巩固练习

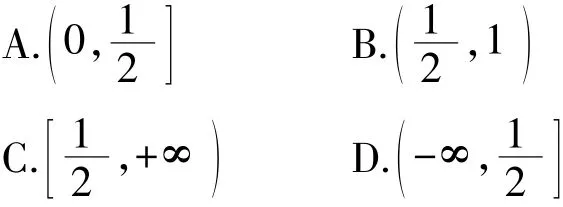
参考答案：

1.A2.B3.0，1]（4.（-∞，0）∪（0，1）

二、不可分离参数的函数零点问题的处理策略

不可分离参数的函数零点问题往往以复合函数的形式出现，处理这类问题的关键是采用换元法将内外层函数分开，再利用分离参数的方法研究.这类问题的处理方式有两种：一是由内而外分析.研究由于自变量的变化导致内层函数变化，再研究由内层函数的变化导致外层函数变化；二是将内层函数进行换元，由外而内进行研究.下面我们对这两种研究方式举例说明.

例5已知函数若f（f（x））=t有 3 个零点，则 t的取值范围是 ____.

【解析】f（x）的图像如图所示：

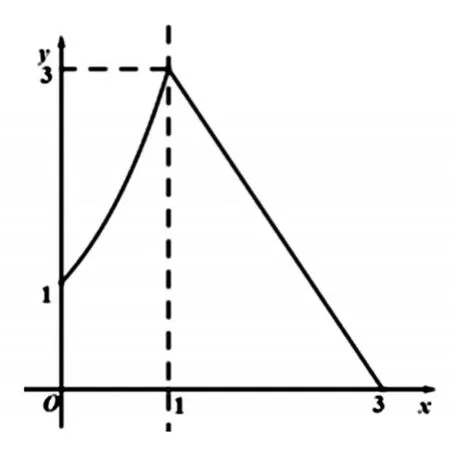
令 f（x）=m，

则由于x的变化，m随之变化，进而f（m）随之变化.

其变化情况如下表：

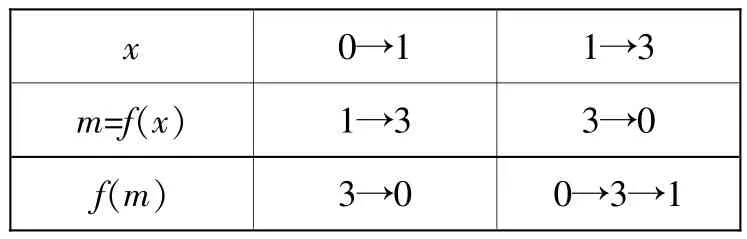
x 0→1　1→3 m=f（x）　1→3　3→0 f（m）　3→0　0→3→1

因此 f（f（x））=t解的情况可由下图分析：

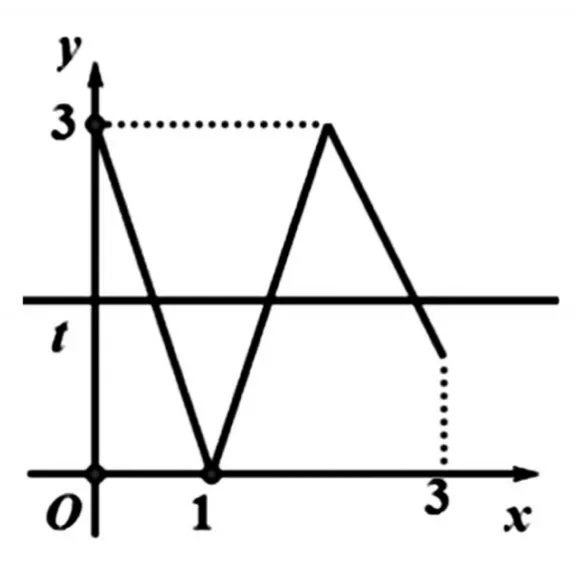
由图像分析得，要使 f（f（x））=t有 3 个零点，只需 1≤t＜3 即可.

例6已知y=f（x）是定义域为R的偶函数，当，若关于x的方程[f（x）]2+af（x）+b=0（a，b∈R）有且仅有6个不同的实数根，则实数a的取值范围是____.

【解析】作出函数 f（x）的图像如下：

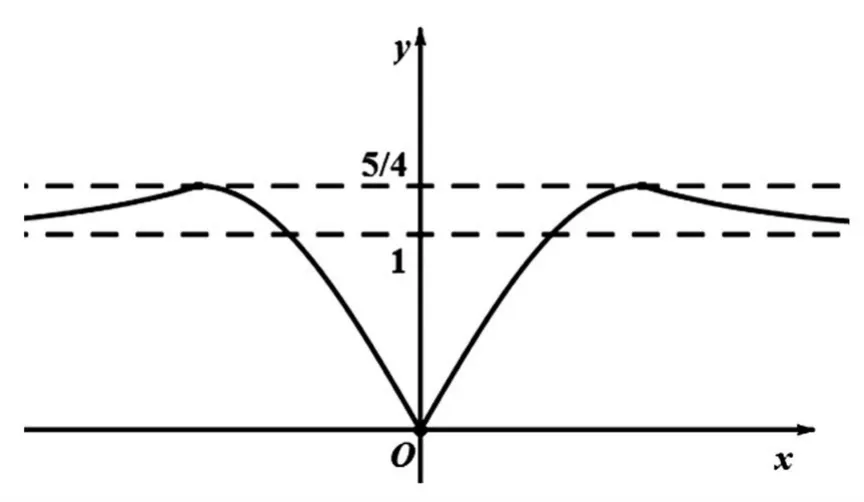
如图可知， f（x）在（-∞，-2）和（0，2）上递增，在（-2，0）和（2，+∞）上递减，

当 x=0 时，函数取得最小值 f（0）=0.

要使关于x的方程

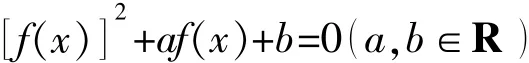
有且仅有6个不同实数根，

设 t=f（x），

当 t＜0，方程 t=f（x）有 0 个根，

当 t=0，方程 t=f（x）有 1 个根，

则t2+at+b=0必有两个根t1、t2，

则有两种情况符合题意：

例7已知函数，方程 f2（x）+tf（x）+1=0（t∈R）有四个实数根，则t的取值范围是____.

其函数图像如图所示：

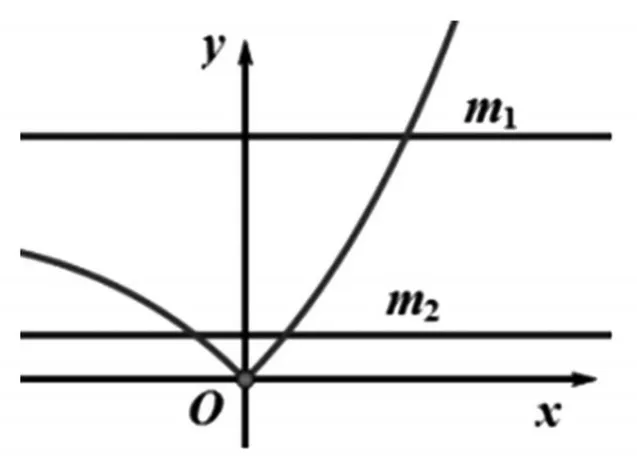
要使方程 f2（x）+tf（x）+1=0（t∈R）有四个实根，令f（x）=m，则方程m2+tm+1=0应有两个不等根m1，m2，且

【总结提升】

1.复合函数的零点问题处理方法有两种：

一是由内及外的分析方法，例5研究的思路是由x的变化分析m的变化情况，再研究f（m）的变化规律.进而利用分离参数的方法解决.

二是由外及内的分析方法，如例6设t=f（x），进而将问题转换成t2+at+b=0的两个实根t1、t2与f（x）的交点个数问题.

2.例7和例6相比区别在于：m1，m2的范围不仅仅是，还要满足 mm=1，这样才12导致了t的范围发生了进一步的改变.同学们思考一下将例6中的b改成又会有什么改变？（提示：两根之差为定值）

巩固练习

1.已知函数f（x）=3sin2x-sinx+a在x∈0，2π）[有两个不同的零点，求实数a的取值范围.

参考答案：

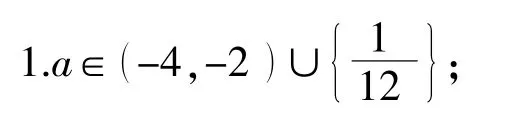
2.c=0，-1＜b＜0；

3.b＜-2；

4.[1，54）

本文主要针对含参函数的零点问题进行研究，考生要把握好怎样分离参数，分离出哪种形式才能使问题的解决更加简洁，同时注意整理化简时零点个数是否发生改变，最终把问题转换成两个函数图像相交交点个数问题来处理，采用动静结合的方式，形象直观地找出符合题意的解.对于复合函数的零点问题要把握好内外两层函数之间的关系，采用由内而外或者由外而内的思路，利用换元法转换成可以分离参数的形式去解决.只要我们适当转换灵活应对，相信在考试中一能取得优异成绩，祝同学们2017高考成功！