迷宫密封结构设计优化
刘勇,梁崇治
(东方汽轮机有限公司,四川德阳,618000)
迷宫密封结构设计优化
刘勇,梁崇治
(东方汽轮机有限公司,四川德阳,618000)
耦合Kriging代理模型、迷宫密封参数化方法和自适应差分进化算法,在数值验证的基础上,完成了某迷宫式密封多目标鲁棒性设计优化。优化时,选取压比和密封间隙作为不确定性变量,同时选取齿厚等10个几何参数作为优化变量,以迷宫密封泄漏量的均值及其方差最小为目标,进行多目标优化。优化后,在给定压比和间隙条件下,最优设计泄漏量降低了29.85%,在压比及间隙同时变化时,密封性能提升同样明显,从而验证了多目标设计优化方法的正确性。
迷宫式密封,多目标优化,Kriging代理模型
0 引言
迷宫式密封由于寿命长、结构简单、非接触式等优点被广泛应用于叶轮机械中[1]。密封中的泄漏损失会影响叶轮机械的效率及输出功率。迷宫密封中流动现象复杂,其泄漏特性受到运行工况、结构参数等多种因素的影响。因此,采用优化方法以提高密封的性能是当前常用的手段。Schramm等[2]采用模拟退火优化算法对某三齿阶梯迷宫密封进行了优化,使得泄漏量降低了10%。Braun等[3]提出了针对不同类型的迷宫密封的通用优化工具。Wang等[4]采用径向基函数优化了某离心压气机的迷宫密封,优化后,密封的泄漏量显著降低,同时叶轮的等熵效率提高了2%。Cremanns等[5]采用自主研发的混合响应面方法,以降低密封泄漏量和总焓降为目标,对某迷宫密封进行了多目标优化。
值得注意的是,密封齿的设计加工及运行过程存在诸多不确定性。首先,热胀冷缩以及几何加工误差都会造成密封齿间隙相对设计值产生较大偏差,从而严重影响密封性能。另外,由于汽轮机各级组进出口压力会发生波动,级前后压比发生变化,对汽轮机密封性能也会产生较大影响。如何减轻上述由于加工、运行工况乃至环境变化所导致的不确定因素对汽轮机性能的影响,设计出适用范围广、鲁棒性好的密封结构,是当前设计中的一个难点。
近年来,关于鲁棒性(稳健性)设计优化的研究,因其对工程实际的重要意义而受到了广泛的关注。在确定性优化中,是以提高产品的名义性能为目标,而未能考虑到加工、运行等过程中的不确定性的影响。鲁棒性设计优化是追求产品的性能稳健性,降低性能受外界不确定因素影响的优化方法[6]。本文将Kriging代理模型[7]与多目标进化算法[8]相结合,以泄漏量的均值和方差作为目标函数,对迷宫式密封进行多目标设计优化。
1 多目标设计优化方法
1.1 迷宫密封多目标设计优化流程
耦合迷宫密封参数化方法、Kriging响应面以及自适应多目标差分进化算法(SMODE),发展了多目标设计优化方法,对迷宫齿型密封进行了多目标设计优化,如图1所示。该方法包括4个阶段,首先在空间均匀采样的基础上,采用CFD进行性能评估;其次利用Kriging响应面建立输入与输出之间的近似模型;接下来利用自适应多目标差分进化算法,以性能函数均值和方差作为目标函数开展多目标优化;最后,通过流场分析阐明最优设计泄漏量降低的本质原因。
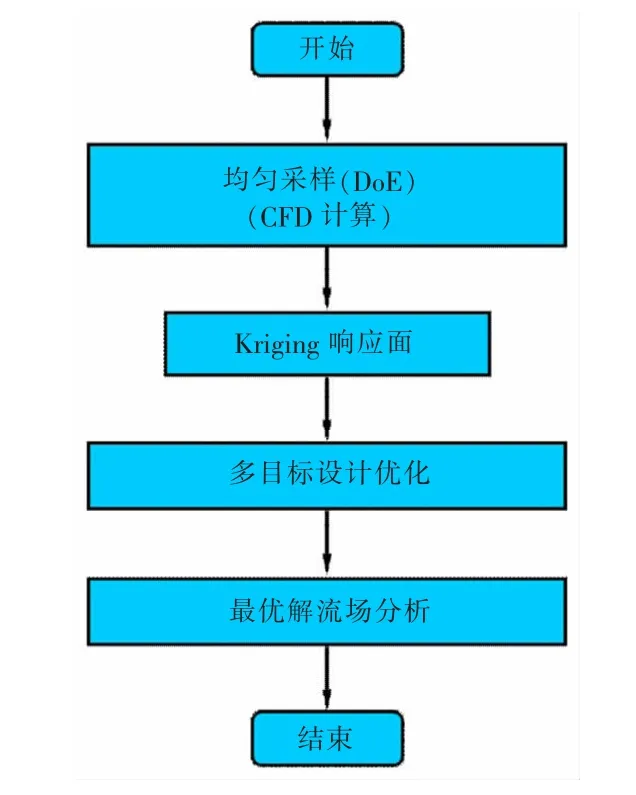
图1 多目标设计优化流程
1.2 迷宫密封参数化方法
基于参考设计的迷宫齿型密封,本文进一步考虑了斜齿的倾角、根部的倒角以及顶部的型线,密封进出口的凹槽以及出口处的凸台等结构对于密封性能的影响,建立的迷宫齿型密封参数化方法如图2所示。

图2 迷宫密封参数化方法
根据相关经验,选取齿厚t、倾角β、倒角半径δ、进口凹槽位置d1、进口凹槽半径R1、出口凹槽位置d2、出口凹槽半径R2、控制点5(a,Δ)共10个变量作为优化变量,选取间隙c和进出口压比PR作为不确定性变量,而空腔的高度d及密封轴向总长L保持不变,如表1所示。

表1 设计变量
1.3 优化目标与约束条件
本文选取12个设计变量对迷宫齿型密封进行鲁棒性多目标设计优化。其中,密封齿间隙和压比作为不确定性变量,服从均匀分布;其余10个设计变量如齿厚、倒角半径等作为优化变量。优化过程中,选取在密封齿间隙和压比变化时密封平均泄漏量最小,并且泄漏量方差变化最小为目标函数,进行多目标设计优化。考虑到密封齿结构的特点,对齿厚与密封齿间距之间的关系进行约束,相应的表达式如下:
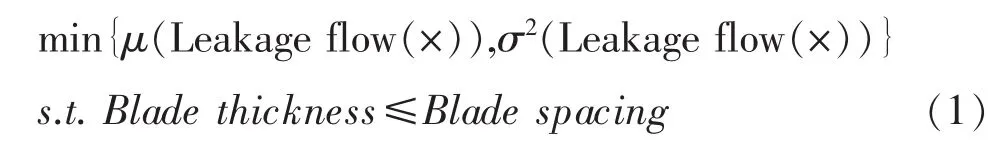
2 设计优化实例
2.1 数值计算方法
2.1.1 几何模型
图3给出了文献[9]中某典型迷宫密封的几何模型,本文将其作为参考设计,其具体几何参数如表2所示。
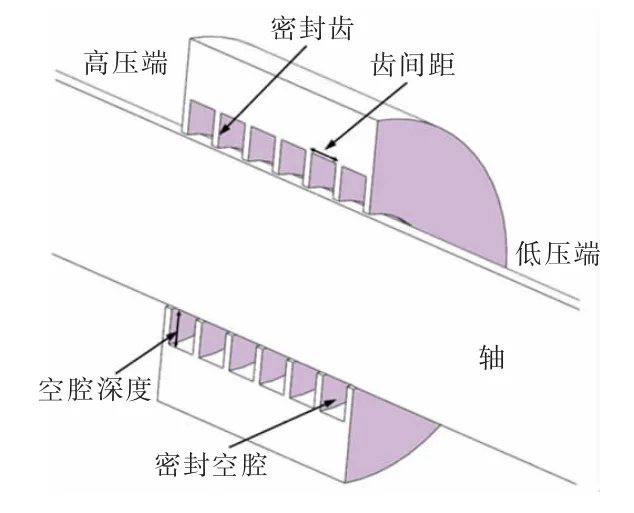
图3 某典型迷宫密封的几何模型

表2 参考设计的几何参数
2.1.2 计算模型和边界条件
本文采用商业软件CFX求解RANS方程,预测迷宫密封的泄漏特性。湍流模型采用标准k-ε模型。计算中,考虑到周期性,取一部分弧段作为研究对象,弧段的两侧采用旋转周期性边界,计算模型如图4所示。
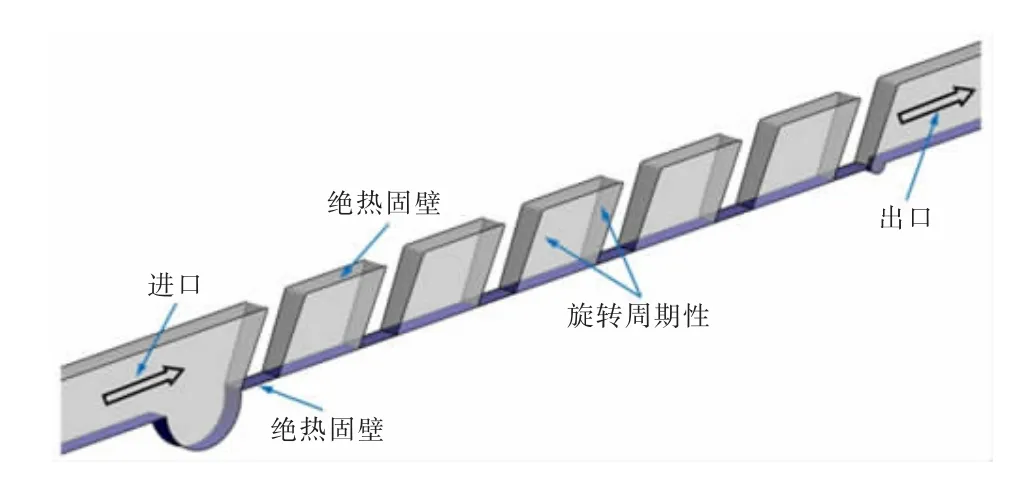
图4 计算模型
进口给定总温、总压,出口给定平均静压,工质采用理想气体。计算不同压比时,改变进口总压,其余保持不变,表3给出了压比PR=0.367时的边界条件。其中,压比的定义为出口静压与进口总压之比。

表3 PR=0.367时的边界条件
计算的收敛标准为:动量方程残差达到10-6数量级,质量方程残差小于10-6数量级,进出口流量相差小于0.1%。
2.1.3 计算网格
本文采用ICEM软件生成结构化网格,计算网格如图5所示。为了提高网格质量,在倒角区域和凹槽区域采用O型网格剖分,其余区域采用H型网格剖分。对壁面网格进行加密,保证y+满足湍流模型的要求。在节流间隙处沿径向布置12个网格节点,以捕捉间隙内复杂的流动特征。经过网格无关性验证,最终网格规模确定为65万。

图5 计算网格
2.2 数值方法验证
图6给出了不同压比下,数值计算的泄漏量与实验值的对比,可以看出,当压比较小时,计算值偏低;当压比较大时,计算值偏高;在中等压比时,两者吻合最好,其中,最大误差小于14.5%,说明本文所采用的数值计算方法是正确、可行的。
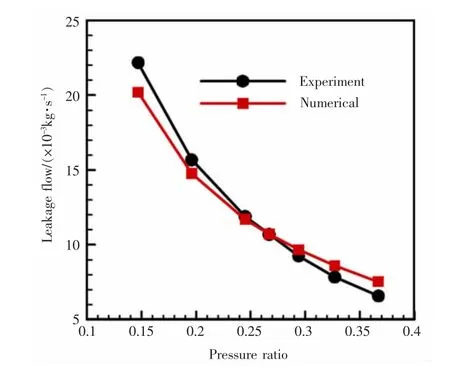
图6 数值验证结果
2.3 优化结果分析
图7给出了多目标优化后得到的Pareto最优解集,优化后,迷宫密封泄漏量的均值和方差均显著降低。
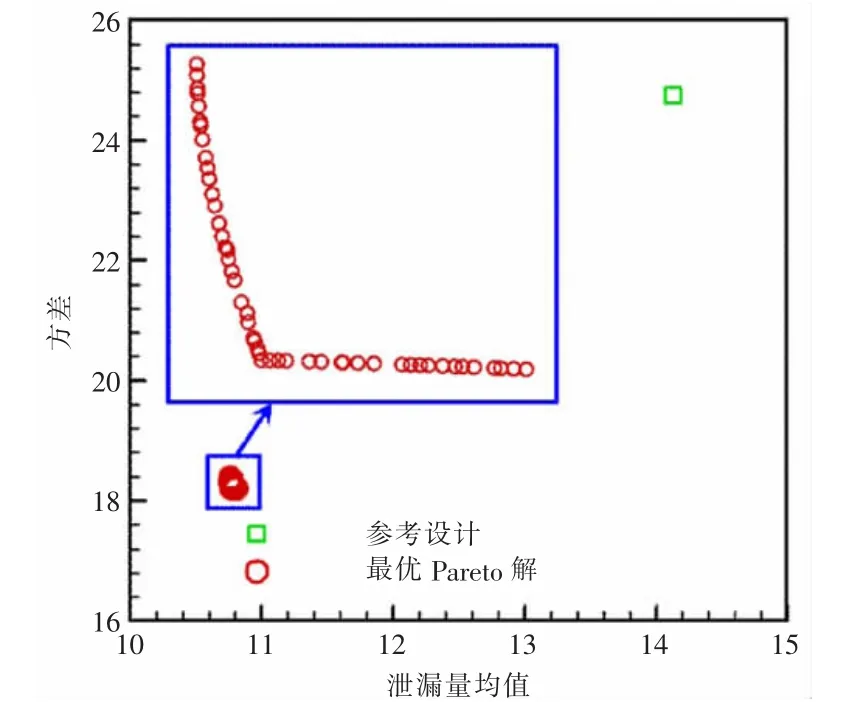
图7 Pareto最优解集
图8给出了优化前、后的型线对比。其中,t、Δ、R1取极大值,R2、β、d1、d2取极小值,而倒角半径δ和凸台高度H取中间值。

图8 优化前后几何对比
图9给出了优化前后第一个齿总压分布,可以看出,齿厚t越大,节流间隙内的节流效应越强,导致更多的动能转化为热能,因而最优设计密封齿出口处的总压更低。

图9 优化前、后第一个齿处总压分布
图10给出了优化前、后最后一个齿处的马赫数分布,可以看出,齿厚越大,最后一个齿间隙出口的马赫数越低,因而最优设计泄漏量越低。

图10 优化前、后最后一个齿处马赫数分布
图11给出了优化前、后不同位置处马赫数的分布,可以看出优化后,节流间隙处的速度分布明显不同于参考设计。因为Δ导致此处的流动会经历一个先收缩再扩张的过程,有利于节流效应的产生,降低优化设计的泄漏量。

图11 优化前、后不同位置处马赫数分布
图12比较了优化前、后第2个齿附近的马赫数和流线分布,可知齿的倾斜改变了齿入口处的速度分布,有利于降低泄漏量。
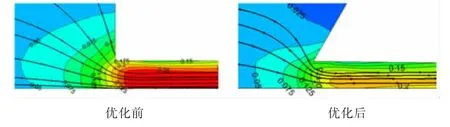
图12 优化前、后第2个齿附近马赫数和流线分布
表4定量对比了鲁棒性优化前、后密封的总体性能,近似模型所预测的泄漏量与CFD计算的结果相差在3%以内,从而验证了近似模型的可靠性。优化后,最优设计相对参考设计的泄漏量均值降低23.64%,方差降低26.39%。将压比PR和节流间隙c固定时,泄漏量降低30%左右,表明最优设计相对参考设计密封性能明显提高。
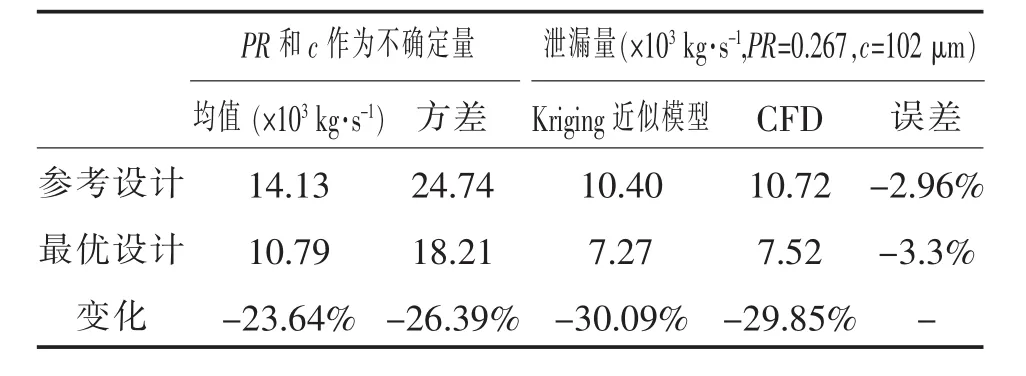
表4 优化前/后密封总体性能比较
图13比较了不同压比时优化前、后的泄漏量,可知,不同压比时优化后的泄漏量相比于参考设计均降低,且压比越小时,降低越明显。从图14可知,不同节流间隙时,优化后的泄漏量均降低,且节流间隙越大,降低越明显。从而验证了鲁棒性设计优化的正确性和有效性。

图13 不同压比时性能比较

图14 不同节流间隙时性能比较
3 结论
本文耦合基于Kriging代理模型的鲁棒性多目标优化方法、不确定性量化方法,带有复杂结构的迷宫齿型密封参数化方法和三维RANS方程求解技术,建立了迷宫齿型密封鲁棒性多目标设计优化方法。
基于该方法,本文完成了迷宫齿型密封鲁棒性多目标优化。优化后,最优设计相对参考设计的泄漏量均值降低23.64%,方差降低26.39%。将压比PR和节流间隙c固定时,泄漏量降低30%左右,表明优化后迷宫密封性能明显提高。
[1]We Soto E A,Childs D W.Experimental rotordynamic coefficient results for(a)a labyrinth seal with and without shunt injection and(b)a honeycomb seal[J].Journal of Engineering for Gas Turbines and Power,1999,121(1):153-159.
[2]Schramm V,Denecke J,Kim S,et al.Shape optimization of a labyrinth seal applying the simulated annealing method[J]. International Journal of Rotating Machinery,2004,10(5):365-371.
[3]Braun E,Dullenkopf K,Bauer H J.Optimization of labyrinth seal performance combining experimental,numerical and data mining methods[C].ASME Paper,GT2012-68077.
[4]Wang Z,Xu L,Xi G.Numerical investigation on the labyrinth seal design for a low flow coefficient centrifugal compressor[C].ASME Paper,GT2010-23096.
[5]Cremanns K,Roos D,Hecker S,et al.Efficient multi-objective optimization of labyrinth seal leakage in steam turbines based on hybrid surrogate model[C].ASME Paper, GT2016-57457.
[6]Park G J,Lee T H,Lee K H,et al.Robust Design:An Overview[J].AIAA Journal,2006,44(1):181-191.
[7]郭振东,宋立明,李军,等.基于子元模型的全局优化与设计空间知识挖掘方法[J],推进技术,2015,36(2):207-216.
[8]Song Liming,Luo Chang,Li Jun,et al.Automated Multiobjective and Multidisciplinary Design Optimization of a Transonic Turbine Stages[J].Journal of Power and Energy, 2012,226(2):262-276.
[9]Gamal A J,Vance J M.Labyrinth seal leakage tests:tooth profile,tooth thickness and eccentricity effects[J].Journal of Engineering for Gas Turbines and Power,2008,130(1):012510.
Shape Optimization of a Labyrinth Seal Configuration
Liu Yong,Liang Chongzhi
(Dongfang Turbine Co.,Ltd.,Deyang Sichuan,618000)
A multi-objective robust optimization method is proposed and implemented for the design of a labyrinth seal upon numerical validation.This method combines the Kriging surrogate model with parameterization method of a labyrinth seal,and selfadaptive multi-objective differential evolution algorithm(SMODE)as well.The multi-objective optimization is conducted for minimizing averaged leakage flow with minimum variance.In the optimization process,pressure ratio and seal clearance are set as uncertainty variables,and other 10 geometrical parameters are set as optimization variables.After optimization,the leakage flow rate of the optimal solution is reduced by 29.85%when pressure ratio and seal clearance are set as constant.And such smaller leakage flow maintained when pressure ratio and seal clearance are varied.Therefore,the correctness and effectiveness of the proposed method is demonstrated.
labyrinth seal,multi-objective optimization,Kriging surrogate model
TK402
A
1674-9987(2017)02-0016-05
10.13808/j.cnki.issn1674-9987.2017.02.005
刘勇(1977-),男,工学学士,工程师,毕业于重庆工学院机械制造及自动化专业,主要从事汽轮机加工工艺设计、质量管理工作。

